人教版数学八年级下册第十八章平行四边形单元综合练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册第十八章平行四边形单元综合练习(含解析) | 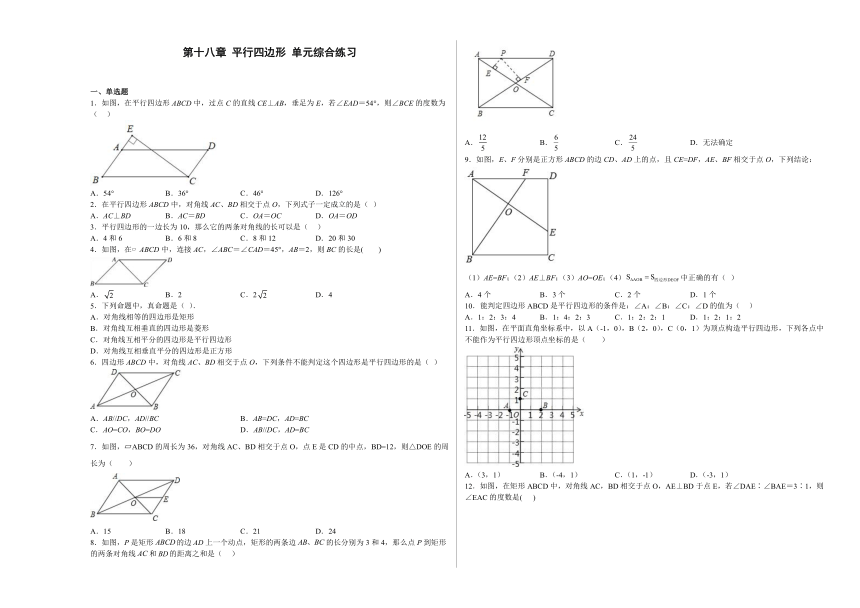 | |
| 格式 | zip | ||
| 文件大小 | 405.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 17:24:20 | ||
图片预览




文档简介
第十八章 平行四边形 单元综合练习
一、单选题
1.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为( )
A.54° B.36° C.46° D.126°
2.在平行四边形ABCD中,对角线AC、BD相交于点O,下列式子一定成立的是( )
A.AC⊥BD B.AC=BD C.OA=OC D.OA=OD
3.平行四边形的一边长为10,那么它的两条对角线的长可以是( )
A.4和6 B.6和8 C.8和12 D.20和30
4.如图,在 ABCD中,连接AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
A. B.2 C.2 D.4
5.下列命题中,真命题是( ).
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
6.四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB//DC,AD//BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB//DC,AD=BC
7.如图, ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A.15 B.18 C.21 D.24
8.如图,P是矩形的边上一个动点,矩形的两条边的长分别为3和4,那么点P到矩形的两条对角线和的距离之和是( )
A. B. C. D.无法确定
9.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:
(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.能判定四边形ABCD是平行四边形的条件是:∠A:∠B:∠C:∠D的值为( )
A.1:2:3:4 B.1:4:2:3 C.1:2:2:1 D.1:2:1:2
11.如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A.(3,1) B.(-4,1) C.(1,-1) D.(-3,1)
12.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若∠DAE∶∠BAE=3∶1,则∠EAC的度数是( )
A.18° B.36° C.45° D.72°
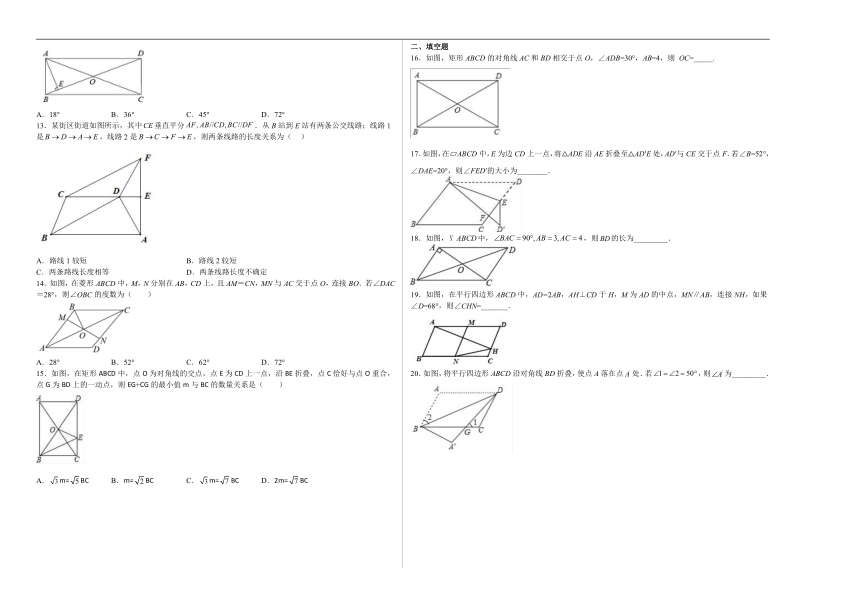
13.某街区街道如图所示,其中垂直平分.从B站到E站有两条公交线路;线路1是,线路2是,则两条线路的长度关系为( )
A.路线1较短 B.路线2较短
C.两条路线长度相等 D.两条线路长度不确定
14.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
15.如图,在矩形ABCD中,点O为对角线的交点,点E为CD上一点,沿BE折叠,点C恰好与点O重合,点G为BD上的一动点,则EG+CG的最小值m与BC的数量关系是( )
A.m=BC B.m=BC C.m=BC D.2m=BC
二、填空题
16.如图,矩形ABCD的对角线AC和BD相交于点O,∠ADB=30°,AB=4,则 OC=_____.
17.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为________.
18.如图,中,,则的长为_________.
19.如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN=_______.
20.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点处.若,则为_________.
三、解答题
21.如图,在四边形中,,,,是的中点.点以每秒个单位长度的速度从点出发,沿向点运动;点同时以每秒个单位长度的速度从点出发,沿向点运动.点停止运动时,点也随之停止运动.当运动时间为多少秒时,以点,,,为顶点的四边形是平行四边形.
22.如图,在□ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25°,求∠C、∠B的度数.
23.如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
24.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF 的面积.
25.如图,□ABCD中,AC为对角线,EF⊥AC于点O,交AD于点E,交BC于点F,连结AF、CE.请你探究当O点满足什么条件时,四边形AFCE是菱形,并说明理由.
参考答案
1.B
【详解】∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠EAD=54°,
∴∠B=∠EAD=54°,
∵CE⊥AB,
∴∠BCE=90°-54°=36°.
故选:B.
2.C
【详解】解:平行四边形的对角线互相平分,
,
则选项一定成立,选项不一定成立,
故选:C.
3.D
【详解】解:如图,设AB=10,对角线相交于点E,
它的两条对角线的长为4和6时,,不符合题意;
它的两条对角线的长为6和8时,,不符合题意;
它的两条对角线的长为8和12时,,不符合题意;
它的两条对角线的长为20和30时,设AE=15,BE=10,,符合题意;
故选:D.
4.C
【详解】解:∵四边形ABCD是平行四边形,
∴CD=AB=2,BC=AD,∠D=∠ABC=∠CAD=45°,
∴AC=CD=2,∠ACD=90°,即△ACD是等腰直角三角形,
∴BC=AD==2.
故选C
5.C
【详解】解:A、两条对角线相等且相互平分的四边形为矩形;故本选项错误;
B、对角线互相垂直的平行四边形是菱形;故本选项错误;
C、对角线互相平分的四边形是平行四边形;故本选项正确;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误.
故选C.
6.D
【详解】解:A、由“AB//DC,AD//BC”可知,四边形ABCD的两组对边互相平行,则该四边形是平行四边形.故本选项不符合题意;
B、由“AB=DC,AD=BC”可知,四边形ABCD的两组对边相等,则该四边形是平行四边形.故本选项不符合题意;
C、由“AO=CO,BO=DO”可知,四边形ABCD的两条对角线互相平分,则该四边形是平行四边形.故本选项不符合题意;
D、由“AB//DC,AD=BC”可知,四边形ABCD的一组对边平行,另一组对边相等,据此不能判定该四边形是平行四边形.故本选项符合题意.
故选D.
7.A
【详解】解:∵ ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,DE=CD,
∴OE是△BCD的中位线,∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
即△DOE的周长为15.
故选A
8.A
【详解】解:如图所示,连接OP,
∵矩形的两条边AB、BC的长分别为3和4,
∴S矩形ABCD=AB BC=12,OA=OC,OB=OD,AC=BD==5,
∴OA=OD=,
∴S△ACD=S矩形ABCD=6,
∴S△AOD=S△ACD=3,
∵S△AOD=S△AOP+S△DOP=OA PE+OD PF=××PE+××PF=(PE+PF)=3,
解得:PE+PF=.
故选:A.
9.B
【详解】解:∵四边形ABCD为正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
而CE=DF,
∴AF=DE,
在△ABF和△DAE中
∴△ABF≌△DAE,
∴AE=BF,所以(1)正确;
∴∠ABF=∠EAD,
而∠EAD+∠EAB=90°,
∴∠ABF+∠EAB=90°,
∴∠AOB=90°,
∴AE⊥BF,所以(2)正确;
连接BE,
∵BE>BC,
∴BA≠BE,
而BO⊥AE,
∴OA≠OE,所以(3)错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF-S△AOF=S△DAE-S△AOF,
∴S△AOB=S四边形DEOF,所以(4)正确.
故选:B.
10.D
【详解】解:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,所以只有D符合条件.
故选D.
两组对角分别相等的四边形是平行四边形,所以∠A和∠C是对角,∠B和∠D是对角,对角的份数应相等.只有选项D符合.
11.B
【详解】如图所示:
①以AC为对角线,可以画出 AFCB,F(-3,1);
②以AB为对角线,可以画出 ACBE,E(1,-1);
③以BC为对角线,可以画出 ACDB,D(3,1),
故选B.
12.C
【详解】试题解析:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∴∠OAB=∠OBA,
∵∠DAE:∠BAE=3:1,
∴∠BAE=×90°=22.5°,
∵AE⊥BD,
∴∠AEB=90°,
∴∠OAB=∠OBA=90°-22.5°=67.5°,
∴∠EAC=67.5°-22.5°=45°.
故选C
13.C
【详解】解:这两条路线路程的长度一样.理由如下:
延长FD交AB于点G.
∵BC∥DF,AB∥DC,
∴四边形BCDG是平行四边形,
∴DG=CB.
∵CE垂直平分AF,
∴FE=AE,DE∥AG,
∴FD=DG,
∴CB=FD.
又∵BC∥DF,
∴四边形BCFD是平行四边形.
∴CF=BD. ①
∵CE垂直平分AF,
∴AE=FE,FD=DA. ②
∴BC=DA. ③
路线1的长度为:BD+DA+AE,路线2的长度为:BC+CF+FE,
综合①②③,可知路线1路程长度与路线2路程长度相等.
故选C.
14.C
【详解】解:∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
∵ ,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=28°,
∴∠BCA=∠DAC=28°,
∴∠OBC=90°﹣28°=62°.
故选:C.
15.C
【详解】如图,由题意,,
是等边三角形,
延长交于,连接交于,连接,
由题意、关于对称,
,
当、、共线时,的值最小,最小值为的长,
设,,
在中,,,
,
在中,,
,
,
.
故选:.
16.4
【详解】解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC,∠BAD=90°,
∵∠ADB=30°,
∴AC=BD=2AB=8,
∴OC=AC=4.
故答案为4.
17.36°
【详解】解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
故答案为36°.
18.
【详解】解:
故答案为:
19.56
【详解】连接MH.∵AH⊥CD于H,M为AD的中点,∴MH=AD=DM,∴∠D=∠MHD=68°.∵MN∥AB,∴∠NMH=∠MHD=68°.又∵MN=AB=AD,∴MN=MH,∴∠MHN=(180°-68°)÷2=56°,∴∠CHN=180°-∠DHM-∠MHN=56°.故答案为56°
点睛:此题主要考查了平行四边形的性质、直角三角形的性质以及等腰三角形的判定和性质,正确地构造出与所求相关的等腰三角形是解决问题的关键.
20.105°.
【详解】∵AD∥BC,∴∠ADB=∠DBG,
由折叠可得∠ADB=∠BDG,∴∠DBG=∠BDG,
又∵∠1=∠BDG+∠DBG=50°,∴∠ADB=∠BDG=25°,
又∵∠2=50°,∴△ABD中,∠A=105°,∴∠A'=∠A=105°,
故答案为105°.
21.当运动时间为秒或秒时,以点,,,为顶点的四边形是平行四边形.
【详解】解:是的中点,
,
①当运动到和之间,设运动时间为,则得:
,
解得:;
②当运动到和之间,设运动时间为,则得:
,
解得:,
当运动时间为秒或秒时,以点,,,为顶点的四边形是平行四边形.
22.∠C=50°,∠B=130°.
【详解】∵∠BAD的平分线AE交DC于E,若∠DAE=25°,
∴∠BAD=50°.
∴在平行四边形ABCD中,∠C=∠BAD=50°,∠B=180°-∠C=130°.
23.(1)证明见解析;(2)证明见解析.
【详解】解:(1)∵△ABC和△BEF都是等边三角形,
∴AB=AC,∠EBF=∠ACB=∠BAC=60°, ∵∠EAD=60°, ∴∠EAD=∠BAC,
∴∠EAB=∠CAD, 在△ABE和△ACD中,∠EBA=∠ACB,AB=AC,∠EAB=∠DAC,
∴△ABE≌△ACD.
(2)由(1)得△ABE≌△ACD, ∴BE=CD, ∵△BEF、△ABC是等边三角形,
∴BE=EF, ∴∠EFB=∠ABC=60°, ∴EF∥CD, ∴BE=EF=CD,
∴EF=CD,且EF∥CD, ∴四边形EFCD是平行四边形.
24.(1)证明详见解析;
(2)证明详见解析;
(3)10.
【详解】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵AD为BC边上的中线,
∴DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=BC,
∴四边形ADCF是菱形;
(3)解:连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCF=AC DF=×4×5=10.
25.当O是AC的中点时,四边形AFCE是菱形,理由见解析.
【详解】解:当O是AC的中点时,四边形AFCE是菱形.
理由如下:连接AF,CE.
∵在 ABCD中,AD∥BC,
∴∠EAO=∠FCO.
∵点O是AC的中点,
∴AO=CO.
又∵∠EOA=∠FOC,
∴△AOE≌△COF,
∴OE=OF.
又∵AO=CO,
∴四边形AFCE是平行四边形.
∴当EF⊥AC时,四边形AFCE是菱形.
一、单选题
1.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为( )
A.54° B.36° C.46° D.126°
2.在平行四边形ABCD中,对角线AC、BD相交于点O,下列式子一定成立的是( )
A.AC⊥BD B.AC=BD C.OA=OC D.OA=OD
3.平行四边形的一边长为10,那么它的两条对角线的长可以是( )
A.4和6 B.6和8 C.8和12 D.20和30
4.如图,在 ABCD中,连接AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
A. B.2 C.2 D.4
5.下列命题中,真命题是( ).
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形是平行四边形
D.对角线互相垂直平分的四边形是正方形
6.四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A.AB//DC,AD//BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB//DC,AD=BC
7.如图, ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A.15 B.18 C.21 D.24
8.如图,P是矩形的边上一个动点,矩形的两条边的长分别为3和4,那么点P到矩形的两条对角线和的距离之和是( )
A. B. C. D.无法确定
9.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:
(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.能判定四边形ABCD是平行四边形的条件是:∠A:∠B:∠C:∠D的值为( )
A.1:2:3:4 B.1:4:2:3 C.1:2:2:1 D.1:2:1:2
11.如图,在平面直角坐标系中,以A(-1,0),B(2,0),C(0,1)为顶点构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是( )
A.(3,1) B.(-4,1) C.(1,-1) D.(-3,1)
12.如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,若∠DAE∶∠BAE=3∶1,则∠EAC的度数是( )
A.18° B.36° C.45° D.72°
13.某街区街道如图所示,其中垂直平分.从B站到E站有两条公交线路;线路1是,线路2是,则两条线路的长度关系为( )
A.路线1较短 B.路线2较短
C.两条路线长度相等 D.两条线路长度不确定
14.如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
15.如图,在矩形ABCD中,点O为对角线的交点,点E为CD上一点,沿BE折叠,点C恰好与点O重合,点G为BD上的一动点,则EG+CG的最小值m与BC的数量关系是( )
A.m=BC B.m=BC C.m=BC D.2m=BC
二、填空题
16.如图,矩形ABCD的对角线AC和BD相交于点O,∠ADB=30°,AB=4,则 OC=_____.
17.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为________.
18.如图,中,,则的长为_________.
19.如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN=_______.
20.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点处.若,则为_________.
三、解答题
21.如图,在四边形中,,,,是的中点.点以每秒个单位长度的速度从点出发,沿向点运动;点同时以每秒个单位长度的速度从点出发,沿向点运动.点停止运动时,点也随之停止运动.当运动时间为多少秒时,以点,,,为顶点的四边形是平行四边形.
22.如图,在□ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25°,求∠C、∠B的度数.
23.如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
24.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF 的面积.
25.如图,□ABCD中,AC为对角线,EF⊥AC于点O,交AD于点E,交BC于点F,连结AF、CE.请你探究当O点满足什么条件时,四边形AFCE是菱形,并说明理由.
参考答案
1.B
【详解】∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠EAD=54°,
∴∠B=∠EAD=54°,
∵CE⊥AB,
∴∠BCE=90°-54°=36°.
故选:B.
2.C
【详解】解:平行四边形的对角线互相平分,
,
则选项一定成立,选项不一定成立,
故选:C.
3.D
【详解】解:如图,设AB=10,对角线相交于点E,
它的两条对角线的长为4和6时,,不符合题意;
它的两条对角线的长为6和8时,,不符合题意;
它的两条对角线的长为8和12时,,不符合题意;
它的两条对角线的长为20和30时,设AE=15,BE=10,,符合题意;
故选:D.
4.C
【详解】解:∵四边形ABCD是平行四边形,
∴CD=AB=2,BC=AD,∠D=∠ABC=∠CAD=45°,
∴AC=CD=2,∠ACD=90°,即△ACD是等腰直角三角形,
∴BC=AD==2.
故选C
5.C
【详解】解:A、两条对角线相等且相互平分的四边形为矩形;故本选项错误;
B、对角线互相垂直的平行四边形是菱形;故本选项错误;
C、对角线互相平分的四边形是平行四边形;故本选项正确;
D、对角线互相垂直平分且相等的四边形是正方形;故本选项错误.
故选C.
6.D
【详解】解:A、由“AB//DC,AD//BC”可知,四边形ABCD的两组对边互相平行,则该四边形是平行四边形.故本选项不符合题意;
B、由“AB=DC,AD=BC”可知,四边形ABCD的两组对边相等,则该四边形是平行四边形.故本选项不符合题意;
C、由“AO=CO,BO=DO”可知,四边形ABCD的两条对角线互相平分,则该四边形是平行四边形.故本选项不符合题意;
D、由“AB//DC,AD=BC”可知,四边形ABCD的一组对边平行,另一组对边相等,据此不能判定该四边形是平行四边形.故本选项符合题意.
故选D.
7.A
【详解】解:∵ ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,DE=CD,
∴OE是△BCD的中位线,∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,
即△DOE的周长为15.
故选A
8.A
【详解】解:如图所示,连接OP,
∵矩形的两条边AB、BC的长分别为3和4,
∴S矩形ABCD=AB BC=12,OA=OC,OB=OD,AC=BD==5,
∴OA=OD=,
∴S△ACD=S矩形ABCD=6,
∴S△AOD=S△ACD=3,
∵S△AOD=S△AOP+S△DOP=OA PE+OD PF=××PE+××PF=(PE+PF)=3,
解得:PE+PF=.
故选:A.
9.B
【详解】解:∵四边形ABCD为正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
而CE=DF,
∴AF=DE,
在△ABF和△DAE中
∴△ABF≌△DAE,
∴AE=BF,所以(1)正确;
∴∠ABF=∠EAD,
而∠EAD+∠EAB=90°,
∴∠ABF+∠EAB=90°,
∴∠AOB=90°,
∴AE⊥BF,所以(2)正确;
连接BE,
∵BE>BC,
∴BA≠BE,
而BO⊥AE,
∴OA≠OE,所以(3)错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF-S△AOF=S△DAE-S△AOF,
∴S△AOB=S四边形DEOF,所以(4)正确.
故选:B.
10.D
【详解】解:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,所以只有D符合条件.
故选D.
两组对角分别相等的四边形是平行四边形,所以∠A和∠C是对角,∠B和∠D是对角,对角的份数应相等.只有选项D符合.
11.B
【详解】如图所示:
①以AC为对角线,可以画出 AFCB,F(-3,1);
②以AB为对角线,可以画出 ACBE,E(1,-1);
③以BC为对角线,可以画出 ACDB,D(3,1),
故选B.
12.C
【详解】试题解析:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=AC,OB=BD,AC=BD,
∴OA=OB,
∴∠OAB=∠OBA,
∵∠DAE:∠BAE=3:1,
∴∠BAE=×90°=22.5°,
∵AE⊥BD,
∴∠AEB=90°,
∴∠OAB=∠OBA=90°-22.5°=67.5°,
∴∠EAC=67.5°-22.5°=45°.
故选C
13.C
【详解】解:这两条路线路程的长度一样.理由如下:
延长FD交AB于点G.
∵BC∥DF,AB∥DC,
∴四边形BCDG是平行四边形,
∴DG=CB.
∵CE垂直平分AF,
∴FE=AE,DE∥AG,
∴FD=DG,
∴CB=FD.
又∵BC∥DF,
∴四边形BCFD是平行四边形.
∴CF=BD. ①
∵CE垂直平分AF,
∴AE=FE,FD=DA. ②
∴BC=DA. ③
路线1的长度为:BD+DA+AE,路线2的长度为:BC+CF+FE,
综合①②③,可知路线1路程长度与路线2路程长度相等.
故选C.
14.C
【详解】解:∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
∵ ,
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=28°,
∴∠BCA=∠DAC=28°,
∴∠OBC=90°﹣28°=62°.
故选:C.
15.C
【详解】如图,由题意,,
是等边三角形,
延长交于,连接交于,连接,
由题意、关于对称,
,
当、、共线时,的值最小,最小值为的长,
设,,
在中,,,
,
在中,,
,
,
.
故选:.
16.4
【详解】解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC,∠BAD=90°,
∵∠ADB=30°,
∴AC=BD=2AB=8,
∴OC=AC=4.
故答案为4.
17.36°
【详解】解:∵四边形ABCD是平行四边形,
∴∠D=∠B=52°,
由折叠的性质得:∠D′=∠D=52°,∠EAD′=∠DAE=20°,
∴∠AEF=∠D+∠DAE=52°+20°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
故答案为36°.
18.
【详解】解:
故答案为:
19.56
【详解】连接MH.∵AH⊥CD于H,M为AD的中点,∴MH=AD=DM,∴∠D=∠MHD=68°.∵MN∥AB,∴∠NMH=∠MHD=68°.又∵MN=AB=AD,∴MN=MH,∴∠MHN=(180°-68°)÷2=56°,∴∠CHN=180°-∠DHM-∠MHN=56°.故答案为56°
点睛:此题主要考查了平行四边形的性质、直角三角形的性质以及等腰三角形的判定和性质,正确地构造出与所求相关的等腰三角形是解决问题的关键.
20.105°.
【详解】∵AD∥BC,∴∠ADB=∠DBG,
由折叠可得∠ADB=∠BDG,∴∠DBG=∠BDG,
又∵∠1=∠BDG+∠DBG=50°,∴∠ADB=∠BDG=25°,
又∵∠2=50°,∴△ABD中,∠A=105°,∴∠A'=∠A=105°,
故答案为105°.
21.当运动时间为秒或秒时,以点,,,为顶点的四边形是平行四边形.
【详解】解:是的中点,
,
①当运动到和之间,设运动时间为,则得:
,
解得:;
②当运动到和之间,设运动时间为,则得:
,
解得:,
当运动时间为秒或秒时,以点,,,为顶点的四边形是平行四边形.
22.∠C=50°,∠B=130°.
【详解】∵∠BAD的平分线AE交DC于E,若∠DAE=25°,
∴∠BAD=50°.
∴在平行四边形ABCD中,∠C=∠BAD=50°,∠B=180°-∠C=130°.
23.(1)证明见解析;(2)证明见解析.
【详解】解:(1)∵△ABC和△BEF都是等边三角形,
∴AB=AC,∠EBF=∠ACB=∠BAC=60°, ∵∠EAD=60°, ∴∠EAD=∠BAC,
∴∠EAB=∠CAD, 在△ABE和△ACD中,∠EBA=∠ACB,AB=AC,∠EAB=∠DAC,
∴△ABE≌△ACD.
(2)由(1)得△ABE≌△ACD, ∴BE=CD, ∵△BEF、△ABC是等边三角形,
∴BE=EF, ∴∠EFB=∠ABC=60°, ∴EF∥CD, ∴BE=EF=CD,
∴EF=CD,且EF∥CD, ∴四边形EFCD是平行四边形.
24.(1)证明详见解析;
(2)证明详见解析;
(3)10.
【详解】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵AD为BC边上的中线,
∴DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=BC,
∴四边形ADCF是菱形;
(3)解:连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCF=AC DF=×4×5=10.
25.当O是AC的中点时,四边形AFCE是菱形,理由见解析.
【详解】解:当O是AC的中点时,四边形AFCE是菱形.
理由如下:连接AF,CE.
∵在 ABCD中,AD∥BC,
∴∠EAO=∠FCO.
∵点O是AC的中点,
∴AO=CO.
又∵∠EOA=∠FOC,
∴△AOE≌△COF,
∴OE=OF.
又∵AO=CO,
∴四边形AFCE是平行四边形.
∴当EF⊥AC时,四边形AFCE是菱形.
