人教版数学八年级下册17.1勾股定理同步练习(含解析)
文档属性
| 名称 | 人教版数学八年级下册17.1勾股定理同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 587.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 17:25:33 | ||
图片预览




文档简介
17.1 勾股定理 同步练习
一、单选题
1.在下列各数中,不是勾股数的是( )
A.5,12,13 B.8, 12, 15 C.8, 15,17 D.9,40,41
2.如图,已知正方形A的面积为3,正方形B的面积为4,则正方形C的面积为( )
A.7 B.5 C.25 D.1
3.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为的半圆,其边缘.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )m.(取3)
A.30 B.28 C.25 D.22
4.已知,斜坡的坡度i=1:2,小明沿斜坡的坡面走了100米,则小明上升的距离是( )
A.米 B.20米 C.米 D.米
5.已知点M的坐标为,则下列说法正确的是( )
A.点M在第二象限内 B.点M到x轴的距离为3
C.点M关于y轴对称的点的坐标为 D.点M到原点的距离为5
6.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
7.观察“赵爽弦图”(如图),若图中四个全等的直角三角形的两直角边分别为a,b,,根据图中图形面积之间的关系及勾股定理,可直接得到等式( )
A. B.
C. D.
8.学校旗杆上的绳子垂到地面还多2米,将绳子的下端拉开6米后,下端刚好接触地面,则旗杆的高度为( )
A.8米 B.10米 C.12米 D.14米
9.我国是最早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,并给出了另外一个证明,下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
10.在中,,点D为中点,绕点D旋转,、分别与边、交于E、F两点.下列结论:
①;②始终为等腰直角三角形;③;④.其中正确的是( )
A.①②③④ B.①④ C.②③ D.①②③
二、填空题
11.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,则A,B两点间的距离为___m.
12.如图,在平面直角坐标系中,以O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的坐标为(-,0),点P的纵坐标为-1,则P点的坐标为 ______.
13.已知长方形ABCD的长为5,宽为4,点E,F分别位于AB,AD上,且,点G是长方形ABCD上一点,是直角三角形,则的斜边长为______.
14.观察下列几组勾股数,并填空:①6,8,10,②8,15,17,③10,24,26,④12,35,37,则第⑥组勾股数为______.
15.如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE=,则AB的长是 _____.
三、解答题
16.如图,把长方形纸片沿折叠,使点落在边上的点处,点落在点处.
(1)试说明;
(2)设,,,试猜想,,之间的关系,并说明理由.
17.长清的园博园广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所,某校七年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?
18.如图,在△ABC中,∠B=45°,∠C=30°,边AC的垂直平分线分别交边BC、AC于点D、E,DC=6.求AB的长.
参考答案
1.B.
【详解】解:A、52+122=132,是勾股数,此选项不符合题意;
B、82+122≠152,不是勾股数,此选项符合题意;
C、82+152=172,是勾股数,此选项不符合题意;
D、92+402=412,是勾股数,此选项不符合题意;
故选:B.
2.A
【详解】解:∵正方体A的面积为3,正方体B的面积为4,
∴正方体C的面积=3+4=7,
故选:A.
3.C
【详解】其侧面展开图如图:作点C关于AB的对称点F,连接DF,
∵中间可供滑行的部分的截面是半径为2.5cm的半圆,
∴BC=πR=2.5π=7.5cm,AB=CD=20cm,
∴CF=2BC=15cm,
在Rt△CDF中,DF=cm,
故他滑行的最短距离约为cm.
故选C.
4.A
【详解】解:如图:
由题意可知:,米,
设米,则米,
由勾股定理可得:,即,
解得:米,米(舍去).
故选:A
5.D
【详解】解:∵点M的坐标为,
∴点M在第四象限,故A选项错误,不符合题意;
点M到x轴的距离是=4,故B选项错误,不符合题意;
点M关于y轴对称的点的坐标为,故C选项错误,不符合题意;
点M到原点的距离为=5,故D选项正确,符合题意,
故选:D.
6.B
【详解】把圆柱沿着点A所在母线展开,如图所示,
作点A的对称点B,
连接PB,
则PB为所求,
根据题意,得PC=8,BC=6,
根据勾股定理,得PB=10,
故选B.
7.C
【详解】标记如下:
∵,
∴(a﹣b)2=a2+b2﹣4
=a2﹣2ab+b2.
故选:C.
8.A
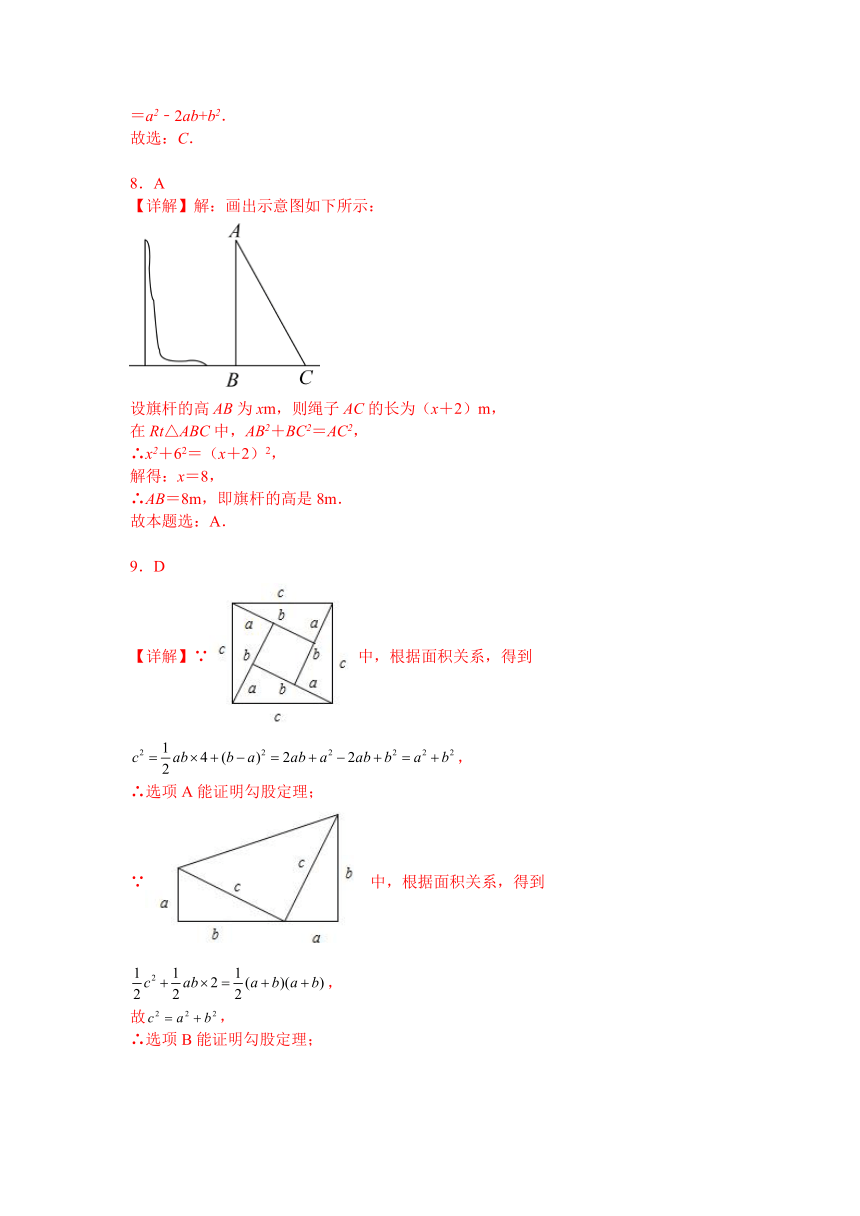
【详解】解:画出示意图如下所示:
设旗杆的高AB为xm,则绳子AC的长为(x+2)m,
在Rt△ABC中,AB2+BC2=AC2,
∴x2+62=(x+2)2,
解得:x=8,
∴AB=8m,即旗杆的高是8m.
故本题选:A.
9.D
【详解】∵中,根据面积关系,得到
,
∴选项A能证明勾股定理;
∵中,根据面积关系,得到
,
故,
∴选项B能证明勾股定理;
∵中,根据面积关系,得到
,
故,
∴选项C能证明勾股定理;
∵中,根据面积关系,得到
,
∴选项D不能证明勾股定理;
故选:D.
10.D.
【详解】解:如图所示,连接,
,点为中点,,
,,,
,
,
.
在和中,
,
,
,,.
,
,
.
,
.
,,
,
,故①正确;
,,
始终为等腰直角三角形,故②正确;
,
,
又,
,故③正确;
,,
,
又,
,故④错误;
正确的有①②③.
故选:D.
.
11.
【详解】在Rt△ABC 中,∠CAB=90゜,AC=20m,BC=60m,由勾股定理得:
(m)
即A、B两点间的距离为m.
故答案为:.
12.(-4,-1)
【详解】解:过P作PB⊥OA于B,
∵点A的坐标为(-,0),
∴OP=OA=,
∵点P的纵坐标为-1,
∴PB=1,
∴OB==4,
∴P点的坐标为(-4,-1),
故答案为:(-4,-1).
13.或或
【详解】解:在长方形ABCD中,∠A=∠B=∠D=90°,AB=CD=4,AD=BC=5,
如图,若∠EGF=90°,点G与点A重合时,是直角三角形,
∴的斜边长为;
如图,若∠GFE=90°,
∵AE=AF=3,
∴△AEF是等腰直角三角形,
∴∠AEF=45°,
∴△BEG为等腰直角三角形,
∴BG=BE=AB-AE=1,
∴,
∴;
如图,若∠EFG=90°,
∵AE=AF=3,
∴△AEF是等腰直角三角形,
∴∠AFE=45°,
∴△DFG为等腰直角三角形,
∴DG=DF=AD-AF=2,
∴,
∴;
综上所述,的斜边长为或或.
故答案为:或或
14.16,63,65
【详解】解:根据题目给出的前几组数的规律可得:这组数中的第一个数是2(n+2),第二个是:(n+1)(n+3),第三个数是:(n+2)2+1,
故可得第⑥组勾股数是16,63,65.
故答案为选:16,63,65.
15.12
【详解】如图,延长BE交AD于点F,
∵点E是DC的中点,
∴DE=CE,
∵AB⊥BC,AB⊥AD,
∴AD∥BC,
∴∠ D=∠BCE,∠FED=∠BEC,
∴ △BCE≌△FDE(ASA),
∴DF=BC=5,BE=EF,
∴BF=2BE=13,AF=5,
在Rt△ABF中,由勾股定理可得AB=12.
故答案为:12.
16.(1)证明见解析;(2),,之间的关系是.理由见解析.
【详解】(1)由折叠的性质 ,得,,
在长方形纸片中,,
∴,
∴,
∴,
∴.
(2),,之间的关系是.理由如下:
由(1)知,由折叠的性质,
得,,.
在中,,
所以,所以.
17.(1)风筝的高度CE为21.6米;
(2)他应该往回收线8米.
【详解】(1)解:在Rt△CDB中,
由勾股定理得,CD2=BC2-BD2=252-152=400,
所以,CD=20(负值舍去),
所以,CE=CD+DE=20+1.6=21.6(米),
答:风筝的高度CE为21.6米;
(2)解:由题意得,CM=12米,
∴DM=8米,
∴BM= (米),
∴BC-BM=25-17=8(米),
∴他应该往回收线8米.
18.AB=.
【详解】解:过点A作AF⊥BC于F,
∵DE垂直平分AC,
∴EA=EC,AD=CD=6,
∵∠C=30°,
∴∠DAC=∠C=30°,
∴DE=,
∴CE=AE==,
∴AC=2EC=,
∴AF=,
∵∠B=45°,AF⊥BC,
∴∠BAF=180°-∠B-∠AFB=180°-45°-90°=45°,
∴∠BAF=∠B,
∴BF=AF=
∴AB=×.
一、单选题
1.在下列各数中,不是勾股数的是( )
A.5,12,13 B.8, 12, 15 C.8, 15,17 D.9,40,41
2.如图,已知正方形A的面积为3,正方形B的面积为4,则正方形C的面积为( )
A.7 B.5 C.25 D.1
3.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为的半圆,其边缘.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )m.(取3)
A.30 B.28 C.25 D.22
4.已知,斜坡的坡度i=1:2,小明沿斜坡的坡面走了100米,则小明上升的距离是( )
A.米 B.20米 C.米 D.米
5.已知点M的坐标为,则下列说法正确的是( )
A.点M在第二象限内 B.点M到x轴的距离为3
C.点M关于y轴对称的点的坐标为 D.点M到原点的距离为5
6.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是( )
A.厘米 B.10厘米 C.厘米 D.8厘米
7.观察“赵爽弦图”(如图),若图中四个全等的直角三角形的两直角边分别为a,b,,根据图中图形面积之间的关系及勾股定理,可直接得到等式( )
A. B.
C. D.
8.学校旗杆上的绳子垂到地面还多2米,将绳子的下端拉开6米后,下端刚好接触地面,则旗杆的高度为( )
A.8米 B.10米 C.12米 D.14米
9.我国是最早了解勾股定理的国家之一.据《周髀算经》记载,勾股定理的公式与证明是在商代由商高发现的,故又称之为“商高定理”;三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释,并给出了另外一个证明,下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
10.在中,,点D为中点,绕点D旋转,、分别与边、交于E、F两点.下列结论:
①;②始终为等腰直角三角形;③;④.其中正确的是( )
A.①②③④ B.①④ C.②③ D.①②③
二、填空题
11.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,则A,B两点间的距离为___m.
12.如图,在平面直角坐标系中,以O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的坐标为(-,0),点P的纵坐标为-1,则P点的坐标为 ______.
13.已知长方形ABCD的长为5,宽为4,点E,F分别位于AB,AD上,且,点G是长方形ABCD上一点,是直角三角形,则的斜边长为______.
14.观察下列几组勾股数,并填空:①6,8,10,②8,15,17,③10,24,26,④12,35,37,则第⑥组勾股数为______.
15.如图,AB⊥BC于点B,AB⊥AD于点A,点E是CD中点,若BC=5,AD=10,BE=,则AB的长是 _____.
三、解答题
16.如图,把长方形纸片沿折叠,使点落在边上的点处,点落在点处.
(1)试说明;
(2)设,,,试猜想,,之间的关系,并说明理由.
17.长清的园博园广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所,某校七年级(1)班的小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为15米;②根据手中剩余线的长度计算出风筝线BC的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度CE;
(2)如果小明想风筝沿CD方向下降12米,则他应该往回收线多少米?
18.如图,在△ABC中,∠B=45°,∠C=30°,边AC的垂直平分线分别交边BC、AC于点D、E,DC=6.求AB的长.
参考答案
1.B.
【详解】解:A、52+122=132,是勾股数,此选项不符合题意;
B、82+122≠152,不是勾股数,此选项符合题意;
C、82+152=172,是勾股数,此选项不符合题意;
D、92+402=412,是勾股数,此选项不符合题意;
故选:B.
2.A
【详解】解:∵正方体A的面积为3,正方体B的面积为4,
∴正方体C的面积=3+4=7,
故选:A.
3.C
【详解】其侧面展开图如图:作点C关于AB的对称点F,连接DF,
∵中间可供滑行的部分的截面是半径为2.5cm的半圆,
∴BC=πR=2.5π=7.5cm,AB=CD=20cm,
∴CF=2BC=15cm,
在Rt△CDF中,DF=cm,
故他滑行的最短距离约为cm.
故选C.
4.A
【详解】解:如图:
由题意可知:,米,
设米,则米,
由勾股定理可得:,即,
解得:米,米(舍去).
故选:A
5.D
【详解】解:∵点M的坐标为,
∴点M在第四象限,故A选项错误,不符合题意;
点M到x轴的距离是=4,故B选项错误,不符合题意;
点M关于y轴对称的点的坐标为,故C选项错误,不符合题意;
点M到原点的距离为=5,故D选项正确,符合题意,
故选:D.
6.B
【详解】把圆柱沿着点A所在母线展开,如图所示,
作点A的对称点B,
连接PB,
则PB为所求,
根据题意,得PC=8,BC=6,
根据勾股定理,得PB=10,
故选B.
7.C
【详解】标记如下:
∵,
∴(a﹣b)2=a2+b2﹣4
=a2﹣2ab+b2.
故选:C.
8.A
【详解】解:画出示意图如下所示:
设旗杆的高AB为xm,则绳子AC的长为(x+2)m,
在Rt△ABC中,AB2+BC2=AC2,
∴x2+62=(x+2)2,
解得:x=8,
∴AB=8m,即旗杆的高是8m.
故本题选:A.
9.D
【详解】∵中,根据面积关系,得到
,
∴选项A能证明勾股定理;
∵中,根据面积关系,得到
,
故,
∴选项B能证明勾股定理;
∵中,根据面积关系,得到
,
故,
∴选项C能证明勾股定理;
∵中,根据面积关系,得到
,
∴选项D不能证明勾股定理;
故选:D.
10.D.
【详解】解:如图所示,连接,
,点为中点,,
,,,
,
,
.
在和中,
,
,
,,.
,
,
.
,
.
,,
,
,故①正确;
,,
始终为等腰直角三角形,故②正确;
,
,
又,
,故③正确;
,,
,
又,
,故④错误;
正确的有①②③.
故选:D.
.
11.
【详解】在Rt△ABC 中,∠CAB=90゜,AC=20m,BC=60m,由勾股定理得:
(m)
即A、B两点间的距离为m.
故答案为:.
12.(-4,-1)
【详解】解:过P作PB⊥OA于B,
∵点A的坐标为(-,0),
∴OP=OA=,
∵点P的纵坐标为-1,
∴PB=1,
∴OB==4,
∴P点的坐标为(-4,-1),
故答案为:(-4,-1).
13.或或
【详解】解:在长方形ABCD中,∠A=∠B=∠D=90°,AB=CD=4,AD=BC=5,
如图,若∠EGF=90°,点G与点A重合时,是直角三角形,
∴的斜边长为;
如图,若∠GFE=90°,
∵AE=AF=3,
∴△AEF是等腰直角三角形,
∴∠AEF=45°,
∴△BEG为等腰直角三角形,
∴BG=BE=AB-AE=1,
∴,
∴;
如图,若∠EFG=90°,
∵AE=AF=3,
∴△AEF是等腰直角三角形,
∴∠AFE=45°,
∴△DFG为等腰直角三角形,
∴DG=DF=AD-AF=2,
∴,
∴;
综上所述,的斜边长为或或.
故答案为:或或
14.16,63,65
【详解】解:根据题目给出的前几组数的规律可得:这组数中的第一个数是2(n+2),第二个是:(n+1)(n+3),第三个数是:(n+2)2+1,
故可得第⑥组勾股数是16,63,65.
故答案为选:16,63,65.
15.12
【详解】如图,延长BE交AD于点F,
∵点E是DC的中点,
∴DE=CE,
∵AB⊥BC,AB⊥AD,
∴AD∥BC,
∴∠ D=∠BCE,∠FED=∠BEC,
∴ △BCE≌△FDE(ASA),
∴DF=BC=5,BE=EF,
∴BF=2BE=13,AF=5,
在Rt△ABF中,由勾股定理可得AB=12.
故答案为:12.
16.(1)证明见解析;(2),,之间的关系是.理由见解析.
【详解】(1)由折叠的性质 ,得,,
在长方形纸片中,,
∴,
∴,
∴,
∴.
(2),,之间的关系是.理由如下:
由(1)知,由折叠的性质,
得,,.
在中,,
所以,所以.
17.(1)风筝的高度CE为21.6米;
(2)他应该往回收线8米.
【详解】(1)解:在Rt△CDB中,
由勾股定理得,CD2=BC2-BD2=252-152=400,
所以,CD=20(负值舍去),
所以,CE=CD+DE=20+1.6=21.6(米),
答:风筝的高度CE为21.6米;
(2)解:由题意得,CM=12米,
∴DM=8米,
∴BM= (米),
∴BC-BM=25-17=8(米),
∴他应该往回收线8米.
18.AB=.
【详解】解:过点A作AF⊥BC于F,
∵DE垂直平分AC,
∴EA=EC,AD=CD=6,
∵∠C=30°,
∴∠DAC=∠C=30°,
∴DE=,
∴CE=AE==,
∴AC=2EC=,
∴AF=,
∵∠B=45°,AF⊥BC,
∴∠BAF=180°-∠B-∠AFB=180°-45°-90°=45°,
∴∠BAF=∠B,
∴BF=AF=
∴AB=×.
