【核心素养目标】3.2.1图形的旋转 教学设计
文档属性
| 名称 | 【核心素养目标】3.2.1图形的旋转 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 14:50:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.2.1图形的旋转教学设计
课题 3.2.1图形的旋转 单元 3 学科 数学 年级 八
教材分析 图形的旋转是在继平移、轴对称之后的又一种图形变换,隐含着重要的变换思想,是培养学生思维能力,树立运动变化观点的好素材。它不仅是本章后续学习中心对称图形的准备,也是今后学习圆的知识内容的铺垫,是构建学生数学知识体系并形成相应的数学技能的重要内容。
核心素养分析 从生活中提取旋转现象,丰富学生学习数学的现实情境,在激发学生学习兴趣的同时也加强数学知识与现实生活的联系,培养学生良好的数学应用意识;经历对生活中旋转图形的观察、讨论、实践操作,使学生充分感知数学美,培养学生学习数学的兴趣和热爱生活的情感.
学习 目标 1.通过具体活动认识平面图形的旋转,理解旋转的基本含义.能准确找到图形旋转时的旋转中心与旋转角。 2.探索旋转的基本性质,理解旋转前后两个图形对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角彼此相等.
重点 类比平移与旋转的异同,掌握旋转的定义和基本性质,并利用数学知识解释生活中的旋转现象。
难点 认识探索、归纳旋转的性质,并用规范的语言进行表述特别是对应点到旋转中心的距离相等。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 向学生展示下面几幅动态图片 (1)上面场景中的转动现象,有什么共同特征? (2)风力发电机的叶片、钟表的指针、摩天轮在转动过程中,其形状、大小、位置是否发生改变? 引导学生列举出一些具有旋转现象的生活实例 创设生活中的问题情境,用生活中的实际例子让学生感受到身边的数学美。激发学生学习的兴趣,调动学生解决疑问,探索知识的积极性。
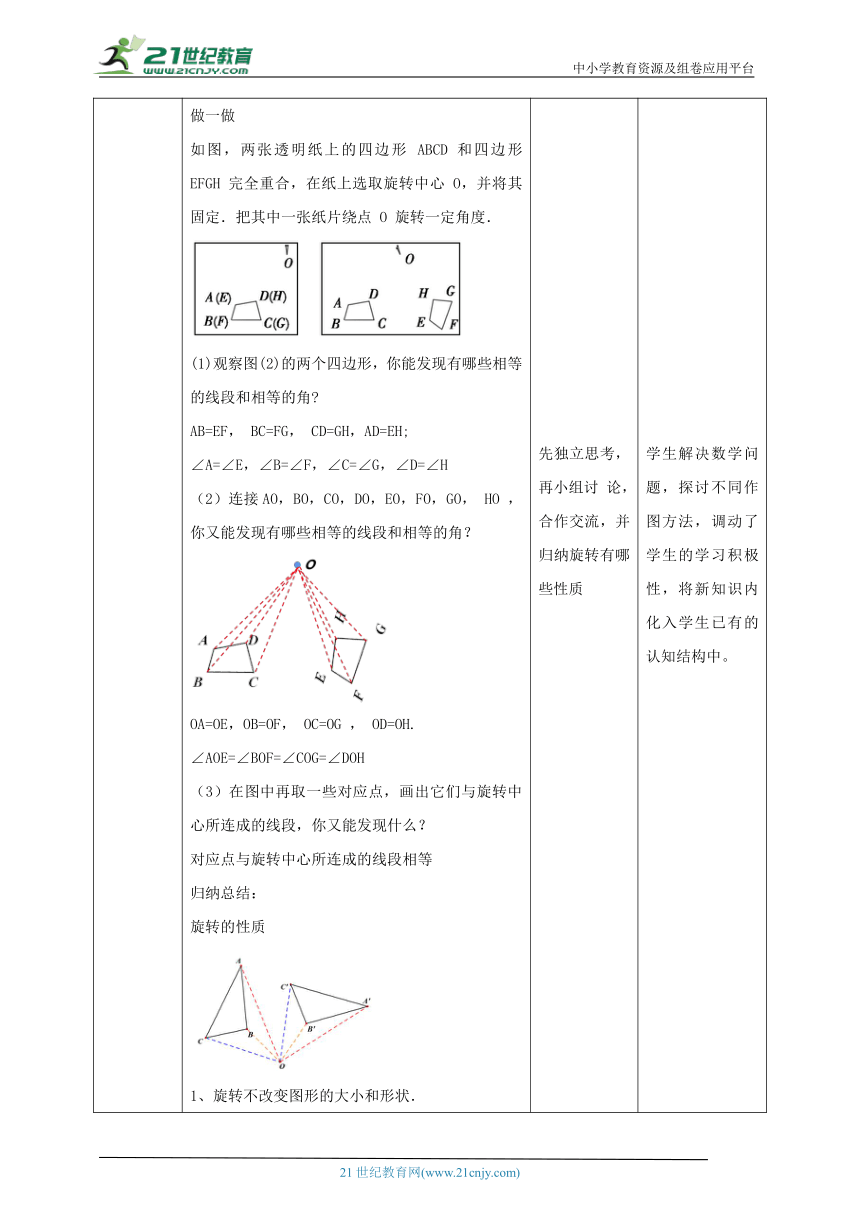
讲授新课 旋转的定义: 在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转. 这个定点称为旋转中心. 转动的角称为旋转角. 旋转不改变图形的形状和大小. 如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点. 转动的方向分为顺时针与逆时针. 确定一次图形的旋转时, 必须明确 旋转角:是对应点与旋转中心所连线段的夹角 旋转不改变图形的形状和大小 温馨提示:①旋转的范围是“平面内”; ②旋转变换同样属于全等变换. 如图所示,△ABC绕点O按顺时针方向旋转一个角度,得到△DEF,点A,B,C分别旋转到了点D,E,F. 点A与点D是一组对应点, 线段AB与线段DE是一组对应线段,∠BAC与∠EDF是一组对应角. 在这一旋转过程中,点O是旋转中心,∠AOD,∠BOE,∠COF都是旋转角. 做一做 如图,两张透明纸上的四边形 ABCD 和四边形 EFGH 完全重合,在纸上选取旋转中心 O,并将其固定.把其中一张纸片绕点 O 旋转一定角度. (1)观察图(2)的两个四边形,你能发现有哪些相等的线段和相等的角 AB=EF, BC=FG, CD=GH,AD=EH; ∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H (2)连接AO,BO,CO,DO,EO,FO,GO, HO ,你又能发现有哪些相等的线段和相等的角? OA=OE,OB=OF, OC=OG , OD=OH. ∠AOE=∠BOF=∠COG=∠DOH (3)在图中再取一些对应点,画出它们与旋转中心所连成的线段,你又能发现什么? 对应点与旋转中心所连成的线段相等 归纳总结: 旋转的性质 1、旋转不改变图形的大小和形状. 2、对应线段相等,对应角相等 3、对应点到旋转中心的距离相等. 4、任意一组对应点与旋转中心的连线所成的角都等于旋转角. ①△ABC≌△A'B'C' ②AO=A'O,BO=B'O,CO=C'O ③∠AOA'=∠BOB'=∠COC' 想一想 在下图(1)~(4)的四个三角形中,哪个不能由△ABC经过平移或旋转得到 首先从平移考虑:图(1)可由△ABC平移得到;图(2)、图(3)、图(4)不能通过△ABC平移得到;其次从旋转角度考虑:无论△ABC以哪个点为旋转中心,都无法得到图(2),图(3)、图(4)可以由△ABC经过旋转得到. 综合分析,只有图(2)无法通过△ABC平移或旋转得到. 典例精析 例、如图,四边形ABCD 经过旋转后与四边形ADEF 重合. (1)指出这一旋转的旋转中心和旋转角; (2)写出图中相等的线段和相等的角. 解:(1)旋转中心为A; 旋转角有∠BAD, ∠CAE,∠DAF. (2)相等的线段:AB=AD,AC=AE,AD=AF, BC=DE,CD=EF,AB=AF; 相等的角:∠BAC=∠DAE, ∠BAD=∠CAE=∠DAF,∠CAD=∠EAF, ∠ABC=∠ADE,∠ADC=∠AFE, ∠BCD=∠DEF,∠BCA=∠DEA, ∠ACD=∠AEF. 归纳方法: 旋转的性质的两种应用 (1)根据旋转角相等,对应点与旋转中心的连线相等可得线段或角相等. (2)根据旋转前后的图形与原来图形的形状、大小都相同可得图形的对应线段、对应角相等. 通过观察、思考、交流、讨论得出结论 独立观察,然后全班交流 先独立思考,再小组讨 论,合作交流,并归纳旋转有哪些性质 学生自主完成,并讨论归纳出结论 出示例题,引导学生思考,对于容易出错的地方做讲解。 师生归纳总结。 点明图形旋转中对应点、对应线段及对应角的概念;让学生及时巩固并理解旋转及其相关概念,并为下面探究旋转的性质作好准备。 确定旋转角的确定是学生学习旋转时容易出错的知识点,当旋转中心非图形某定点时最易出现理解偏差。故本环节利用旋转中心在图形外的旋转现象来解析旋转角的结构特点从而得到其定义。 学生解决数学问题,探讨不同作图方法,调动了学生的学习积极性,将新知识内化入学生已有的认知结构中。 这一环节继续探索旋转的特征,通过设置问题的回答,使学生直接观察得出性质。 在例题解答的过程中进一步体会与理解旋转图形的概念及性质。
课堂练习 1、如图,若将△ABC 绕点O 逆时针旋转90°,则顶点B 的对应点B1的坐标为( ) A.(-4,2) B.(-2,4) C.(4,-2) D.(2,-4) 2.如图,将Rt△ABC 绕直角顶点C 顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( ) A.55° B.60° C.65° D.70° 3. 如图,△ABC绕点A逆时针旋转30°得到△ADE,AB=5 cm,BC=8 cm,∠BAC=130°,则AD= = cm, DE= = cm,∠EAC= ∠ = °. 4. 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把 △ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m= ________ . 5、如图,在△ABC 中,AB=AC=1,∠BAC=45°,△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的,连接BE,CF 相交于点D. (1)求证:BE=CF; (2)当四边形ACDE 的四边相等且AC∥DE 时,求BD 的长. 学生定时训练,自主解答,老师订正 通过练习调动学生学习的积极性,使学生思维处于积极状态,达到了培养学生思维的灵活性和创造性,解决问题的目的。
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:3.2.1 图形的旋转 1、三要素:旋转中心、旋转方向、旋转角度 2、性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.2.1图形的旋转教学设计
课题 3.2.1图形的旋转 单元 3 学科 数学 年级 八
教材分析 图形的旋转是在继平移、轴对称之后的又一种图形变换,隐含着重要的变换思想,是培养学生思维能力,树立运动变化观点的好素材。它不仅是本章后续学习中心对称图形的准备,也是今后学习圆的知识内容的铺垫,是构建学生数学知识体系并形成相应的数学技能的重要内容。
核心素养分析 从生活中提取旋转现象,丰富学生学习数学的现实情境,在激发学生学习兴趣的同时也加强数学知识与现实生活的联系,培养学生良好的数学应用意识;经历对生活中旋转图形的观察、讨论、实践操作,使学生充分感知数学美,培养学生学习数学的兴趣和热爱生活的情感.
学习 目标 1.通过具体活动认识平面图形的旋转,理解旋转的基本含义.能准确找到图形旋转时的旋转中心与旋转角。 2.探索旋转的基本性质,理解旋转前后两个图形对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角彼此相等.
重点 类比平移与旋转的异同,掌握旋转的定义和基本性质,并利用数学知识解释生活中的旋转现象。
难点 认识探索、归纳旋转的性质,并用规范的语言进行表述特别是对应点到旋转中心的距离相等。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 向学生展示下面几幅动态图片 (1)上面场景中的转动现象,有什么共同特征? (2)风力发电机的叶片、钟表的指针、摩天轮在转动过程中,其形状、大小、位置是否发生改变? 引导学生列举出一些具有旋转现象的生活实例 创设生活中的问题情境,用生活中的实际例子让学生感受到身边的数学美。激发学生学习的兴趣,调动学生解决疑问,探索知识的积极性。
讲授新课 旋转的定义: 在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转. 这个定点称为旋转中心. 转动的角称为旋转角. 旋转不改变图形的形状和大小. 如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点. 转动的方向分为顺时针与逆时针. 确定一次图形的旋转时, 必须明确 旋转角:是对应点与旋转中心所连线段的夹角 旋转不改变图形的形状和大小 温馨提示:①旋转的范围是“平面内”; ②旋转变换同样属于全等变换. 如图所示,△ABC绕点O按顺时针方向旋转一个角度,得到△DEF,点A,B,C分别旋转到了点D,E,F. 点A与点D是一组对应点, 线段AB与线段DE是一组对应线段,∠BAC与∠EDF是一组对应角. 在这一旋转过程中,点O是旋转中心,∠AOD,∠BOE,∠COF都是旋转角. 做一做 如图,两张透明纸上的四边形 ABCD 和四边形 EFGH 完全重合,在纸上选取旋转中心 O,并将其固定.把其中一张纸片绕点 O 旋转一定角度. (1)观察图(2)的两个四边形,你能发现有哪些相等的线段和相等的角 AB=EF, BC=FG, CD=GH,AD=EH; ∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H (2)连接AO,BO,CO,DO,EO,FO,GO, HO ,你又能发现有哪些相等的线段和相等的角? OA=OE,OB=OF, OC=OG , OD=OH. ∠AOE=∠BOF=∠COG=∠DOH (3)在图中再取一些对应点,画出它们与旋转中心所连成的线段,你又能发现什么? 对应点与旋转中心所连成的线段相等 归纳总结: 旋转的性质 1、旋转不改变图形的大小和形状. 2、对应线段相等,对应角相等 3、对应点到旋转中心的距离相等. 4、任意一组对应点与旋转中心的连线所成的角都等于旋转角. ①△ABC≌△A'B'C' ②AO=A'O,BO=B'O,CO=C'O ③∠AOA'=∠BOB'=∠COC' 想一想 在下图(1)~(4)的四个三角形中,哪个不能由△ABC经过平移或旋转得到 首先从平移考虑:图(1)可由△ABC平移得到;图(2)、图(3)、图(4)不能通过△ABC平移得到;其次从旋转角度考虑:无论△ABC以哪个点为旋转中心,都无法得到图(2),图(3)、图(4)可以由△ABC经过旋转得到. 综合分析,只有图(2)无法通过△ABC平移或旋转得到. 典例精析 例、如图,四边形ABCD 经过旋转后与四边形ADEF 重合. (1)指出这一旋转的旋转中心和旋转角; (2)写出图中相等的线段和相等的角. 解:(1)旋转中心为A; 旋转角有∠BAD, ∠CAE,∠DAF. (2)相等的线段:AB=AD,AC=AE,AD=AF, BC=DE,CD=EF,AB=AF; 相等的角:∠BAC=∠DAE, ∠BAD=∠CAE=∠DAF,∠CAD=∠EAF, ∠ABC=∠ADE,∠ADC=∠AFE, ∠BCD=∠DEF,∠BCA=∠DEA, ∠ACD=∠AEF. 归纳方法: 旋转的性质的两种应用 (1)根据旋转角相等,对应点与旋转中心的连线相等可得线段或角相等. (2)根据旋转前后的图形与原来图形的形状、大小都相同可得图形的对应线段、对应角相等. 通过观察、思考、交流、讨论得出结论 独立观察,然后全班交流 先独立思考,再小组讨 论,合作交流,并归纳旋转有哪些性质 学生自主完成,并讨论归纳出结论 出示例题,引导学生思考,对于容易出错的地方做讲解。 师生归纳总结。 点明图形旋转中对应点、对应线段及对应角的概念;让学生及时巩固并理解旋转及其相关概念,并为下面探究旋转的性质作好准备。 确定旋转角的确定是学生学习旋转时容易出错的知识点,当旋转中心非图形某定点时最易出现理解偏差。故本环节利用旋转中心在图形外的旋转现象来解析旋转角的结构特点从而得到其定义。 学生解决数学问题,探讨不同作图方法,调动了学生的学习积极性,将新知识内化入学生已有的认知结构中。 这一环节继续探索旋转的特征,通过设置问题的回答,使学生直接观察得出性质。 在例题解答的过程中进一步体会与理解旋转图形的概念及性质。
课堂练习 1、如图,若将△ABC 绕点O 逆时针旋转90°,则顶点B 的对应点B1的坐标为( ) A.(-4,2) B.(-2,4) C.(4,-2) D.(2,-4) 2.如图,将Rt△ABC 绕直角顶点C 顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( ) A.55° B.60° C.65° D.70° 3. 如图,△ABC绕点A逆时针旋转30°得到△ADE,AB=5 cm,BC=8 cm,∠BAC=130°,则AD= = cm, DE= = cm,∠EAC= ∠ = °. 4. 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把 △ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m= ________ . 5、如图,在△ABC 中,AB=AC=1,∠BAC=45°,△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的,连接BE,CF 相交于点D. (1)求证:BE=CF; (2)当四边形ACDE 的四边相等且AC∥DE 时,求BD 的长. 学生定时训练,自主解答,老师订正 通过练习调动学生学习的积极性,使学生思维处于积极状态,达到了培养学生思维的灵活性和创造性,解决问题的目的。
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:3.2.1 图形的旋转 1、三要素:旋转中心、旋转方向、旋转角度 2、性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
