【新课标】3.2.1图形的旋转 课件(共24张PPT)
文档属性
| 名称 | 【新课标】3.2.1图形的旋转 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 14:56:45 | ||
图片预览




文档简介
(共24张PPT)
3.2.1图形的旋转
北师版八年级下册
教学目标
1.通过具体实例认识旋转,掌握旋转的有关概念及基本性质.
2.能够根据旋转的基本性质进行相关的计算和证明.
新知导入
(1)上面场景中的转动现象,有什么共同特征?
(2)风力发电机的叶片、钟表的指针、摩天轮在转动过程中,其形状、大小、位置是否发生改变?
新知讲解
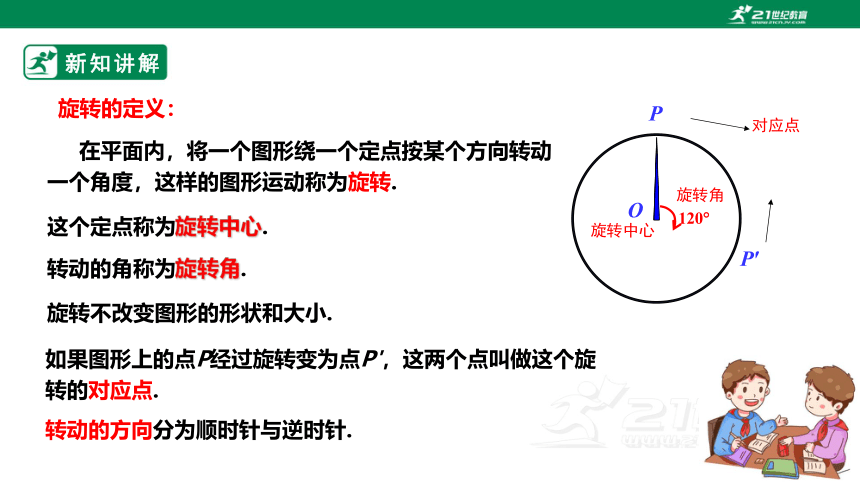
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
旋转的定义:
这个定点称为旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
O
P′
P
旋转中心
旋转角
对应点
旋转不改变图形的形状和大小.
新知讲解
必须明确
确定一次图形的旋转时,
温馨提示:①旋转的范围是“平面内”;
②旋转变换同样属于全等变换.
旋转不改变图形的形状和大小
旋转角:是对应点与旋转中心所连线段的夹角
新知讲解
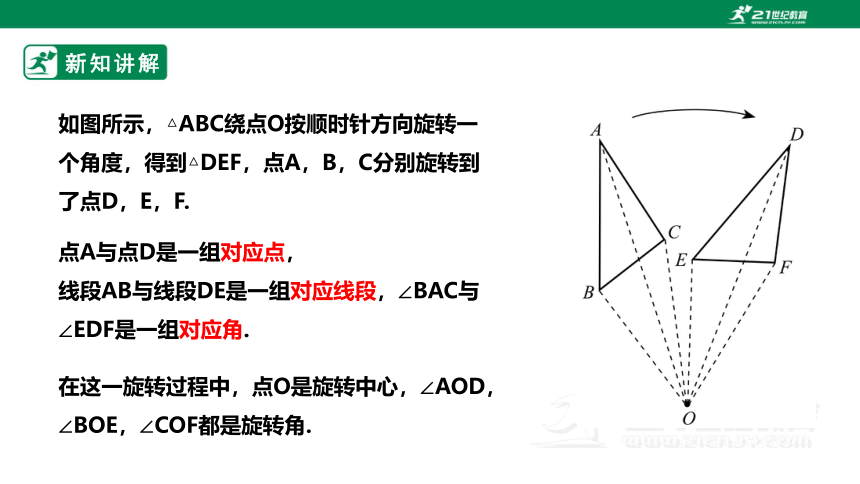
如图所示,△ABC绕点O按顺时针方向旋转一个角度,得到△DEF,点A,B,C分别旋转到了点D,E,F.
点A与点D是一组对应点,
线段AB与线段DE是一组对应线段,∠BAC与∠EDF是一组对应角.
在这一旋转过程中,点O是旋转中心,∠AOD,∠BOE,∠COF都是旋转角.
做一做
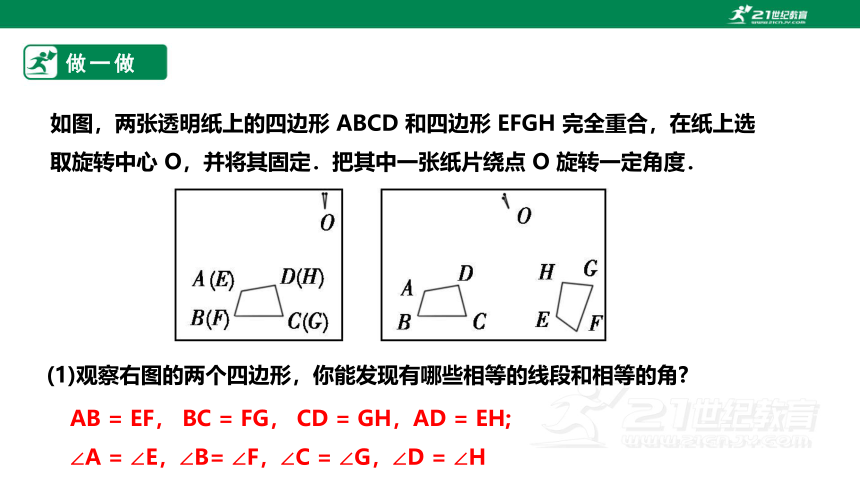
如图,两张透明纸上的四边形 ABCD 和四边形 EFGH 完全重合,在纸上选取旋转中心 O,并将其固定.把其中一张纸片绕点 O 旋转一定角度.
(1)观察右图的两个四边形,你能发现有哪些相等的线段和相等的角
AB = EF, BC = FG, CD = GH,AD = EH;
∠A = ∠E,∠B= ∠F,∠C = ∠G,∠D = ∠H
做一做
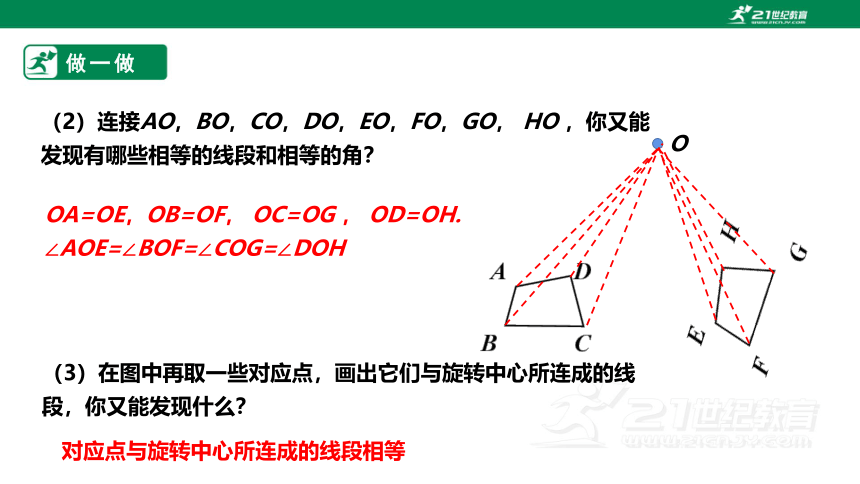
(2)连接AO,BO,CO,DO,EO,FO,GO, HO ,你又能发现有哪些相等的线段和相等的角?
O
OA=OE,OB=OF, OC=OG , OD=OH.
∠AOE=∠BOF=∠COG=∠DOH
(3)在图中再取一些对应点,画出它们与旋转中心所连成的线段,你又能发现什么?
对应点与旋转中心所连成的线段相等
归纳总结
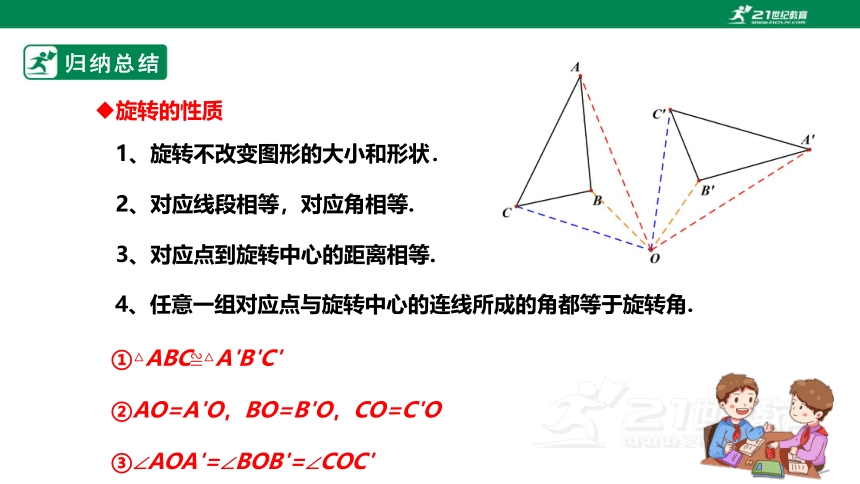
旋转的性质
1、旋转不改变图形的大小和形状.
2、对应线段相等,对应角相等.
3、对应点到旋转中心的距离相等.
4、任意一组对应点与旋转中心的连线所成的角都等于旋转角.
①△ABC≌△A'B'C'
②AO=A'O,BO=B'O,CO=C'O
③∠AOA'=∠BOB'=∠COC'
想一想
在下图(1)~(4)的四个三角形中,哪个不能由△ABC经过平移或旋转得到
首先从平移考虑:图(1)可由△ABC平移得到;图(2)、图(3)、图(4)不能通过△ABC平移得到;其次从旋转角度考虑:无论△ABC以哪个点为旋转中心,都无法得到图(2),图(3)、图(4)可以由△ABC经过旋转得到.
综合分析,只有图(2)无法通过△ABC平移或旋转得到.
典例精析
例、如图,四边形ABCD 经过旋转后与四边形ADEF 重合.
(1)指出这一旋转的旋转中心和旋转角;
(2)写出图中相等的线段和相等的角.
C
E
解:(1)旋转中心为A;
旋转角有∠BAD,
∠CAE,∠DAF.
典例精析
(2)相等的线段:AB=AD,AC=AE,AD=AF,
BC=DE,CD=EF,AB=AF;
相等的角:∠BAC=∠DAE,
∠BAD=∠CAE=∠DAF,∠CAD=∠EAF,
∠ABC=∠ADE,∠ADC=∠AFE,
∠BCD=∠DEF,∠BCA=∠DEA,
∠ACD=∠AEF.
归纳总结
方法总结
旋转的性质的两种应用
(1)根据旋转角相等,对应点与旋转中心的连线相等可得线段或角相等.
(2)根据旋转前后的图形与原来图形的形状、大小都相同可得图形的对应线段、对应角相等.
课堂练习
1.如图,若将△ABC 绕点O 逆时针旋转90°,则顶点B 的对应点B1的坐标为( )
A.(-4,2) B.(-2,4) C.(4,-2) D.(2,-4)
2.如图,将Rt△ABC 绕直角顶点C 顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60° C.65° D.70°
B
C
课堂练习
3. 如图,△ABC绕点A逆时针旋转30°得到△ADE,AB=5 cm,BC=8 cm,
∠BAC=130°,则AD= = cm, DE= = cm,∠EAC=
∠ = °.
AB
5
BC
8
BAD
30
课堂练习
4. 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把 △ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B 恰好落在初始Rt△ABC的边上,那么m= ________ .
80或120
课堂练习
5.如图,在△ABC 中,AB=AC=1,∠BAC=45°,△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的,连接BE,CF 相交于点D.
(1)求证:BE=CF;
(2)当四边形ACDE 的四边相等且AC∥DE 时,求BD 的长.
课堂练习
解:(1)∵△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC.
∴∠EAF+∠BAF=∠BAC+∠BAF,
即∠EAB=∠FAC.
∵AB=AC,∴AE=AF.
∴△AEB ≌ △AFC.
∴BE=CF.
课堂练习
(2)∵四边形ACDE 的四边相等,AB=AC=1,
∴DE=AE=AC=AB=1.
∴∠AEB=∠ABE.
∵AC∥DE,
∴∠ABE=∠BAC=45°.
∴∠AEB=∠ABE=45°.
∴△ABE 为等腰直角三角形.
∴BE=
∴BD=BE-DE=-1.
课堂总结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角
板书设计
课题:3.2.1 图形的旋转
1、三要素:旋转中心、旋转方向、旋转角度
2、性质
作业布置
【必做题】
教材77页习题3.4的1、2
【选做题】
教材第77页习题3.4的3、5题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2.1图形的旋转
北师版八年级下册
教学目标
1.通过具体实例认识旋转,掌握旋转的有关概念及基本性质.
2.能够根据旋转的基本性质进行相关的计算和证明.
新知导入
(1)上面场景中的转动现象,有什么共同特征?
(2)风力发电机的叶片、钟表的指针、摩天轮在转动过程中,其形状、大小、位置是否发生改变?
新知讲解
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
旋转的定义:
这个定点称为旋转中心.
转动的角称为旋转角.
转动的方向分为顺时针与逆时针.
如果图形上的点P经过旋转变为点P',这两个点叫做这个旋转的对应点.
O
P′
P
旋转中心
旋转角
对应点
旋转不改变图形的形状和大小.
新知讲解
必须明确
确定一次图形的旋转时,
温馨提示:①旋转的范围是“平面内”;
②旋转变换同样属于全等变换.
旋转不改变图形的形状和大小
旋转角:是对应点与旋转中心所连线段的夹角
新知讲解
如图所示,△ABC绕点O按顺时针方向旋转一个角度,得到△DEF,点A,B,C分别旋转到了点D,E,F.
点A与点D是一组对应点,
线段AB与线段DE是一组对应线段,∠BAC与∠EDF是一组对应角.
在这一旋转过程中,点O是旋转中心,∠AOD,∠BOE,∠COF都是旋转角.
做一做
如图,两张透明纸上的四边形 ABCD 和四边形 EFGH 完全重合,在纸上选取旋转中心 O,并将其固定.把其中一张纸片绕点 O 旋转一定角度.
(1)观察右图的两个四边形,你能发现有哪些相等的线段和相等的角
AB = EF, BC = FG, CD = GH,AD = EH;
∠A = ∠E,∠B= ∠F,∠C = ∠G,∠D = ∠H
做一做
(2)连接AO,BO,CO,DO,EO,FO,GO, HO ,你又能发现有哪些相等的线段和相等的角?
O
OA=OE,OB=OF, OC=OG , OD=OH.
∠AOE=∠BOF=∠COG=∠DOH
(3)在图中再取一些对应点,画出它们与旋转中心所连成的线段,你又能发现什么?
对应点与旋转中心所连成的线段相等
归纳总结
旋转的性质
1、旋转不改变图形的大小和形状.
2、对应线段相等,对应角相等.
3、对应点到旋转中心的距离相等.
4、任意一组对应点与旋转中心的连线所成的角都等于旋转角.
①△ABC≌△A'B'C'
②AO=A'O,BO=B'O,CO=C'O
③∠AOA'=∠BOB'=∠COC'
想一想
在下图(1)~(4)的四个三角形中,哪个不能由△ABC经过平移或旋转得到
首先从平移考虑:图(1)可由△ABC平移得到;图(2)、图(3)、图(4)不能通过△ABC平移得到;其次从旋转角度考虑:无论△ABC以哪个点为旋转中心,都无法得到图(2),图(3)、图(4)可以由△ABC经过旋转得到.
综合分析,只有图(2)无法通过△ABC平移或旋转得到.
典例精析
例、如图,四边形ABCD 经过旋转后与四边形ADEF 重合.
(1)指出这一旋转的旋转中心和旋转角;
(2)写出图中相等的线段和相等的角.
C
E
解:(1)旋转中心为A;
旋转角有∠BAD,
∠CAE,∠DAF.
典例精析
(2)相等的线段:AB=AD,AC=AE,AD=AF,
BC=DE,CD=EF,AB=AF;
相等的角:∠BAC=∠DAE,
∠BAD=∠CAE=∠DAF,∠CAD=∠EAF,
∠ABC=∠ADE,∠ADC=∠AFE,
∠BCD=∠DEF,∠BCA=∠DEA,
∠ACD=∠AEF.
归纳总结
方法总结
旋转的性质的两种应用
(1)根据旋转角相等,对应点与旋转中心的连线相等可得线段或角相等.
(2)根据旋转前后的图形与原来图形的形状、大小都相同可得图形的对应线段、对应角相等.
课堂练习
1.如图,若将△ABC 绕点O 逆时针旋转90°,则顶点B 的对应点B1的坐标为( )
A.(-4,2) B.(-2,4) C.(4,-2) D.(2,-4)
2.如图,将Rt△ABC 绕直角顶点C 顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
A.55° B.60° C.65° D.70°
B
C
课堂练习
3. 如图,△ABC绕点A逆时针旋转30°得到△ADE,AB=5 cm,BC=8 cm,
∠BAC=130°,则AD= = cm, DE= = cm,∠EAC=
∠ = °.
AB
5
BC
8
BAD
30
课堂练习
4. 如图,Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD.把 △ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B 恰好落在初始Rt△ABC的边上,那么m= ________ .
80或120
课堂练习
5.如图,在△ABC 中,AB=AC=1,∠BAC=45°,△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的,连接BE,CF 相交于点D.
(1)求证:BE=CF;
(2)当四边形ACDE 的四边相等且AC∥DE 时,求BD 的长.
课堂练习
解:(1)∵△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC.
∴∠EAF+∠BAF=∠BAC+∠BAF,
即∠EAB=∠FAC.
∵AB=AC,∴AE=AF.
∴△AEB ≌ △AFC.
∴BE=CF.
课堂练习
(2)∵四边形ACDE 的四边相等,AB=AC=1,
∴DE=AE=AC=AB=1.
∴∠AEB=∠ABE.
∵AC∥DE,
∴∠ABE=∠BAC=45°.
∴∠AEB=∠ABE=45°.
∴△ABE 为等腰直角三角形.
∴BE=
∴BD=BE-DE=-1.
课堂总结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角
板书设计
课题:3.2.1 图形的旋转
1、三要素:旋转中心、旋转方向、旋转角度
2、性质
作业布置
【必做题】
教材77页习题3.4的1、2
【选做题】
教材第77页习题3.4的3、5题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
