2022-2023学年人教版七年级数学下册 6.1.3平方根 课件(共30张PPT)
文档属性
| 名称 | 2022-2023学年人教版七年级数学下册 6.1.3平方根 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 588.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 21:31:37 | ||
图片预览









文档简介
(共30张PPT)
6.1.3 平方根
七年级数学(上册) 人教版
七年级数学组
主 备 人:
议课组长:
议课日期:2023.2.12授课日期:
第六章 实数
1、什么叫算术平方根?它有什么性质?
2、36的算术平方根是____,0的算术平方根是_____,
0.09的算术平方根是_______,
你是怎么求的?用根号如何表示?
思考:平方等于36的数只有6吗?还有哪个数的平方等于36?是______。平方等于0.09的数有几个?______。如何表示呢?
6
0
0.3
-6
2个
若一个正数x的平方等于a,即x =a,则这个正数x为a的
算术平方根。双重非负性
复习引入:(1分钟)
学习目标:(1分钟)
1、掌握平方根和开平方的概念。
2、掌握平方根的性质。
3、能够通过开方运算求一个非负数的平方根及算术平方根。
重点:平方根的概念和性质。
难点:平方根与算术平方根的区别与联系。
探索与思考
若一个数的平方等于9,则这个数为多少?
根据上面的研究过程填表:
1 16 36 49
解:设这个数为a,依题意得:
解得:
自学指导1(6分钟)
认真阅读课本P44-45例4之前的内容,思考完成下列问题:
1.平方根的定义是
_________________________________________________________,
也叫做_________.
2.平方根的性质:一个正数a有____个平方根,表示为______,它们_____________; 0有____个平方根,它是_______;
_____数没有平方根.
3.求一个数a的_________运算,叫做开平方.
一般地,如果一个数x的平方等于a,即x2=a,
那么这个数x就叫做a的平方根
二次方根
两
±
互为相反数
一
0
负
平方根
±
非负数a的平方根表示方法:
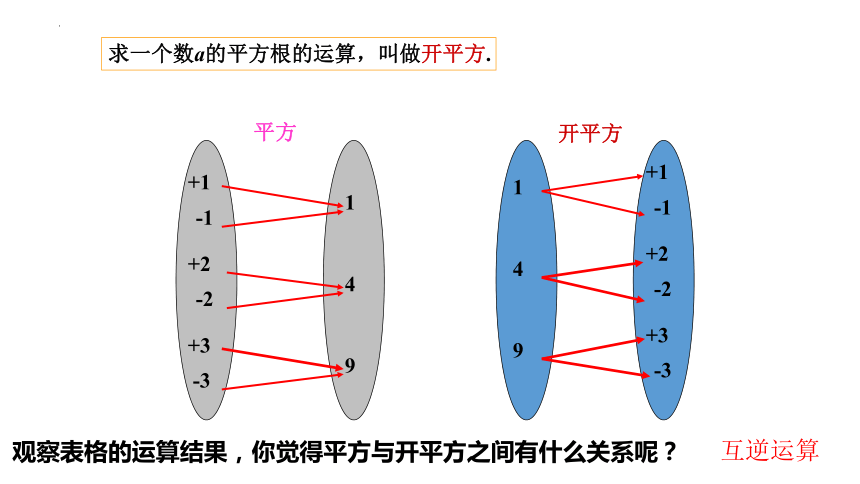
求一个数a的平方根的运算,叫做开平方.
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
观察表格的运算结果,你觉得平方与开平方之间有什么关系呢?
互逆运算
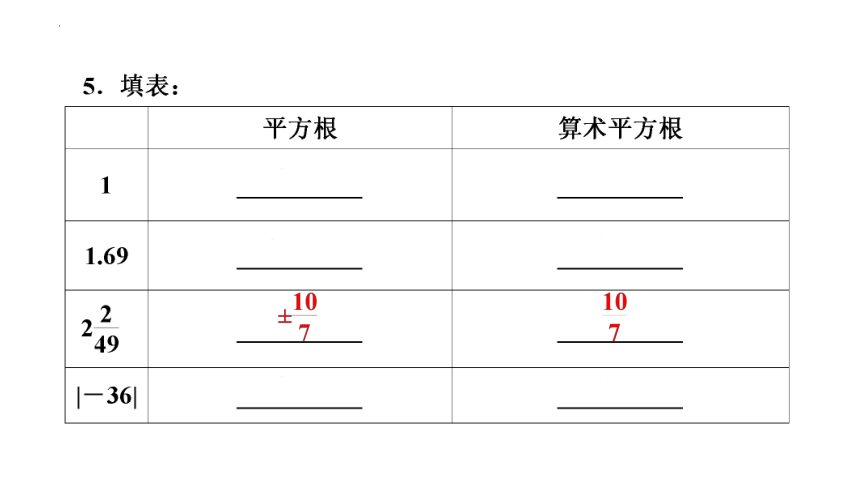
±1
1
±1.3
1.3
±6
6
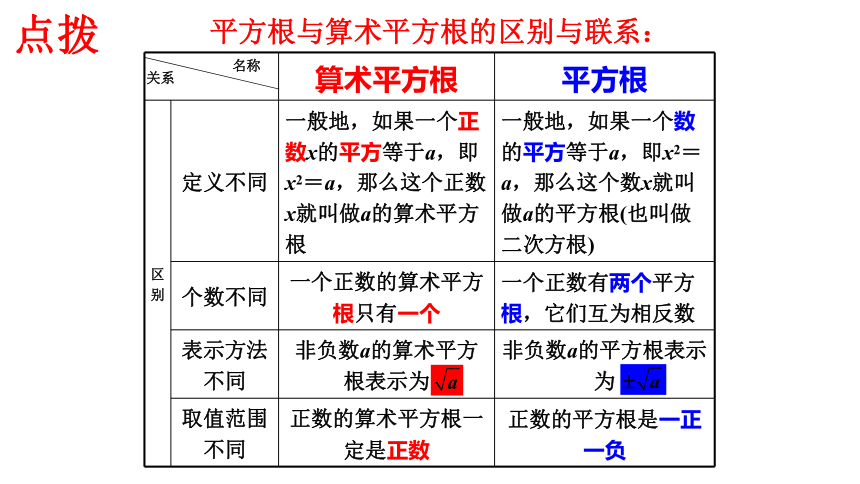
平方根与算术平方根的区别与联系:
算术平方根 平方根
区别 定义不同 一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根 一般地,如果一个数的平方等于a,即x2=a,那么这个数x就叫做a的平方根(也叫做二次方根)
个数不同 一个正数的算术平方根只有一个 一个正数有两个平方根,它们互为相反数
表示方法不同 非负数a的算术平方根表示为 非负数a的平方根表示为
取值范围不同 正数的算术平方根一定是正数 正数的平方根是一正一负
名称
关系
点拨
算术平方根 平方根
联系 具有包含关系 平方根包含算术平方根,算术平方根是平方根中正的那个根(0除外)
存在条件相同 平方根和算术平方根都只有非负数才有,0的平方根与算术平方根都是0
(续表)
名称
关系
1
“± ”的意义是( )
A.a的平方根
B.a的算术平方根
C.当a≥0时,± 是a的平方根
D.以上均不正确
C
1、49的平方根为( )
A.7 B.-7 C.±7 D.±49
C
自学检测1(3分钟)
3、一个正数x的平方根是2a-3和5-a,则a的值是多少,x的值是多少?
2、判断:
(1)-4的平方根是-2; ( )
(2)2是4的平方根; ( )
(3)4的平方根是2; ( )
(4)4的算术平方根是-2. ( )
×
√
×
×
解:依题意得 2a-3+5-a=0
解得:a= -2
当a=-2时,2a-3=2×(-2)-3=-7, ∴ m=(-7)2=49.
自学指导2:(5分钟)
自学课本P45例题4,完成:
1、我们是根据哪个运算来求平方根?
(一定要注意表示法 : )
强调:注意格式的书写
±
随堂练习
(注意书写格式)
求下列各数的平方根:
(1)1.44, (2)0, (3)
(4) (5) 196 (6)
解:
(1)∵(±1.2)2=1.44
∴
1.44的平方根是±1.2
即 = ±1.2
(2)0
(3)
(4)±2
(6)
(5)±14
自学检测2:(5分钟)
1、求下列各数的平方根:
2、求下列各式的值:
3、若
求一个式子的值,先分析式子的意义,特别是看
清它表示的是算术平方根还是平方根,就是看清符号,
最后的结果不改变它的正负性.
与 的化简
自学指导3 (3分钟)
想一想,并完成:
1、求值:
2、
2
3
0.5
2
3
0.5
1.想一想:
(1) = , = , = ,
(2)对于正数a, 等于多少?
2.联系拓广:
对于任意数a, 一定等于a吗?
(a<0)
-a
0
(a=0)
(a>0)
a
不一定相等,只有当a≥0时,它们才相等。当
a<0时, 没有意义。
自学检测3:(5分钟)
1、化简 的结果是( )
A.-4 B.4 C.±4 D.2
B
2.化简: ________;
π-3
3、
解:(2x+1)2 =121
(2x+1)2 =±11
2x+1 =11 或 2x+1=-11
解得: x=5或-6
解: 2(x-1)2 =8
(x-1)2 =4
x-1 =±2
解得: x=3或-1
小结(1分钟)
1.平方根的定义:
2.平方根的性质:正数a有____个平方根; 0的平方根是_______; _____数没有平方根.
两
0
负
一般的,如果一个数X的平方等于a,即X2=a,那么这个数
X叫做a的平方根(也叫做二次方根)。
(a<0)
-a
0
(a=0)
(a>0)
a
3.
4.
1. 的平方根是±16. ( )
2. 一定是正数. ( )
3.a2的算术平方根是a. ( )
4.若 , 则a=-5. ( )
5. ( )
6.-6是(-6)2的平方根. ( )
7.若x2=36,则x= ( )
×
×
×
×
×
√
√
一.判断题
当堂训练: (15分钟)
1、下列各数中,不一定有平方根的是( )
(A)x2+1 (B)|x|+2
(C) (D)|a|-1
D
2、 已知 有意义,则x一定是 ( )
A.正数 B. 负数
C. 非负数 D. 非正数
D
二.选择题:
4. 若 有意义,则 能取的最小整数为( )
(A)0 (B) 1 (C) -1 (D) -4
A
3. 已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是( )
(A) a+1 (B)
(C) a2+1 (D)
D
三.快速回答
4.
3.
2.
1.
9
81
5. 的平方根是 ,算术平方根是 ;(-5)2的平方根是 ,算术平方根是 ;
±5
5
6. 的平方根是 ,算术平方 根是
±2
2
7.若x2=9,则 x= ,若 =3,则 x= ;
8.若(x-1)2=4,则x= ,
±3
3或-1
±3
9.若一个数的一个平方根为-7,则另一个平方根为 ,这个数是 。
7
49
10.平方根等于本身的数是 ;
算术平方根等于它本身的数是 ;算术平方根和平方根相等的数是 。
0
0和1
0
11.如果
,那么
的算术平方根
是什么.
解:由题意得x-4=0 x-y+5=0
x=4 y=9
选做题
1、
2、
解:由题意得2m+1+5-3m=0
解,得 m=6
则两个根 2m+1=13
5-3m=-13
∴这个正数为196
①
解:由题意得2m+3+4m+9=0
解,得 m=-2
则两个根 2m+3=-1
4m+9=1
②
2m+3=4m+9
m=-3
则两个根都是 2m+3=-3
4m+9=-3
1.平方根的定义:
2.平方根的性质:正数a有____个平方根; 0的平方根是_______; _____数没有平方根.
两
0
负
一般的,如果一个数X的平方等于a,即X2=a,那么这个数
X叫做a的平方根(也叫做二次方根)。
(a<0)
-a
0
(a=0)
(a>0)
a
3.
4.
板书设计
平方根的表示
我们已经学过一个正数的算术平方根的表示方法,你能表示一个非负数的平方根吗?
非负数a的算术平方根 ;(正号一般省略)
非负数a的负的平方根 ;
非负数a的平方根 , 读作:正、负根号a
求平方根的写法如下:
如9的平方根,可记作:
5 的平方根,可以记作 和- ,或±
注意:因为负数没有平方根,所以在式子
中的被开方数 a ≥0 ,否则式子 没有意义。
即式子 中的 a 是一个非负数。
6.1.3 平方根
七年级数学(上册) 人教版
七年级数学组
主 备 人:
议课组长:
议课日期:2023.2.12授课日期:
第六章 实数
1、什么叫算术平方根?它有什么性质?
2、36的算术平方根是____,0的算术平方根是_____,
0.09的算术平方根是_______,
你是怎么求的?用根号如何表示?
思考:平方等于36的数只有6吗?还有哪个数的平方等于36?是______。平方等于0.09的数有几个?______。如何表示呢?
6
0
0.3
-6
2个
若一个正数x的平方等于a,即x =a,则这个正数x为a的
算术平方根。双重非负性
复习引入:(1分钟)
学习目标:(1分钟)
1、掌握平方根和开平方的概念。
2、掌握平方根的性质。
3、能够通过开方运算求一个非负数的平方根及算术平方根。
重点:平方根的概念和性质。
难点:平方根与算术平方根的区别与联系。
探索与思考
若一个数的平方等于9,则这个数为多少?
根据上面的研究过程填表:
1 16 36 49
解:设这个数为a,依题意得:
解得:
自学指导1(6分钟)
认真阅读课本P44-45例4之前的内容,思考完成下列问题:
1.平方根的定义是
_________________________________________________________,
也叫做_________.
2.平方根的性质:一个正数a有____个平方根,表示为______,它们_____________; 0有____个平方根,它是_______;
_____数没有平方根.
3.求一个数a的_________运算,叫做开平方.
一般地,如果一个数x的平方等于a,即x2=a,
那么这个数x就叫做a的平方根
二次方根
两
±
互为相反数
一
0
负
平方根
±
非负数a的平方根表示方法:
求一个数a的平方根的运算,叫做开平方.
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
观察表格的运算结果,你觉得平方与开平方之间有什么关系呢?
互逆运算
±1
1
±1.3
1.3
±6
6
平方根与算术平方根的区别与联系:
算术平方根 平方根
区别 定义不同 一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根 一般地,如果一个数的平方等于a,即x2=a,那么这个数x就叫做a的平方根(也叫做二次方根)
个数不同 一个正数的算术平方根只有一个 一个正数有两个平方根,它们互为相反数
表示方法不同 非负数a的算术平方根表示为 非负数a的平方根表示为
取值范围不同 正数的算术平方根一定是正数 正数的平方根是一正一负
名称
关系
点拨
算术平方根 平方根
联系 具有包含关系 平方根包含算术平方根,算术平方根是平方根中正的那个根(0除外)
存在条件相同 平方根和算术平方根都只有非负数才有,0的平方根与算术平方根都是0
(续表)
名称
关系
1
“± ”的意义是( )
A.a的平方根
B.a的算术平方根
C.当a≥0时,± 是a的平方根
D.以上均不正确
C
1、49的平方根为( )
A.7 B.-7 C.±7 D.±49
C
自学检测1(3分钟)
3、一个正数x的平方根是2a-3和5-a,则a的值是多少,x的值是多少?
2、判断:
(1)-4的平方根是-2; ( )
(2)2是4的平方根; ( )
(3)4的平方根是2; ( )
(4)4的算术平方根是-2. ( )
×
√
×
×
解:依题意得 2a-3+5-a=0
解得:a= -2
当a=-2时,2a-3=2×(-2)-3=-7, ∴ m=(-7)2=49.
自学指导2:(5分钟)
自学课本P45例题4,完成:
1、我们是根据哪个运算来求平方根?
(一定要注意表示法 : )
强调:注意格式的书写
±
随堂练习
(注意书写格式)
求下列各数的平方根:
(1)1.44, (2)0, (3)
(4) (5) 196 (6)
解:
(1)∵(±1.2)2=1.44
∴
1.44的平方根是±1.2
即 = ±1.2
(2)0
(3)
(4)±2
(6)
(5)±14
自学检测2:(5分钟)
1、求下列各数的平方根:
2、求下列各式的值:
3、若
求一个式子的值,先分析式子的意义,特别是看
清它表示的是算术平方根还是平方根,就是看清符号,
最后的结果不改变它的正负性.
与 的化简
自学指导3 (3分钟)
想一想,并完成:
1、求值:
2、
2
3
0.5
2
3
0.5
1.想一想:
(1) = , = , = ,
(2)对于正数a, 等于多少?
2.联系拓广:
对于任意数a, 一定等于a吗?
(a<0)
-a
0
(a=0)
(a>0)
a
不一定相等,只有当a≥0时,它们才相等。当
a<0时, 没有意义。
自学检测3:(5分钟)
1、化简 的结果是( )
A.-4 B.4 C.±4 D.2
B
2.化简: ________;
π-3
3、
解:(2x+1)2 =121
(2x+1)2 =±11
2x+1 =11 或 2x+1=-11
解得: x=5或-6
解: 2(x-1)2 =8
(x-1)2 =4
x-1 =±2
解得: x=3或-1
小结(1分钟)
1.平方根的定义:
2.平方根的性质:正数a有____个平方根; 0的平方根是_______; _____数没有平方根.
两
0
负
一般的,如果一个数X的平方等于a,即X2=a,那么这个数
X叫做a的平方根(也叫做二次方根)。
(a<0)
-a
0
(a=0)
(a>0)
a
3.
4.
1. 的平方根是±16. ( )
2. 一定是正数. ( )
3.a2的算术平方根是a. ( )
4.若 , 则a=-5. ( )
5. ( )
6.-6是(-6)2的平方根. ( )
7.若x2=36,则x= ( )
×
×
×
×
×
√
√
一.判断题
当堂训练: (15分钟)
1、下列各数中,不一定有平方根的是( )
(A)x2+1 (B)|x|+2
(C) (D)|a|-1
D
2、 已知 有意义,则x一定是 ( )
A.正数 B. 负数
C. 非负数 D. 非正数
D
二.选择题:
4. 若 有意义,则 能取的最小整数为( )
(A)0 (B) 1 (C) -1 (D) -4
A
3. 已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是( )
(A) a+1 (B)
(C) a2+1 (D)
D
三.快速回答
4.
3.
2.
1.
9
81
5. 的平方根是 ,算术平方根是 ;(-5)2的平方根是 ,算术平方根是 ;
±5
5
6. 的平方根是 ,算术平方 根是
±2
2
7.若x2=9,则 x= ,若 =3,则 x= ;
8.若(x-1)2=4,则x= ,
±3
3或-1
±3
9.若一个数的一个平方根为-7,则另一个平方根为 ,这个数是 。
7
49
10.平方根等于本身的数是 ;
算术平方根等于它本身的数是 ;算术平方根和平方根相等的数是 。
0
0和1
0
11.如果
,那么
的算术平方根
是什么.
解:由题意得x-4=0 x-y+5=0
x=4 y=9
选做题
1、
2、
解:由题意得2m+1+5-3m=0
解,得 m=6
则两个根 2m+1=13
5-3m=-13
∴这个正数为196
①
解:由题意得2m+3+4m+9=0
解,得 m=-2
则两个根 2m+3=-1
4m+9=1
②
2m+3=4m+9
m=-3
则两个根都是 2m+3=-3
4m+9=-3
1.平方根的定义:
2.平方根的性质:正数a有____个平方根; 0的平方根是_______; _____数没有平方根.
两
0
负
一般的,如果一个数X的平方等于a,即X2=a,那么这个数
X叫做a的平方根(也叫做二次方根)。
(a<0)
-a
0
(a=0)
(a>0)
a
3.
4.
板书设计
平方根的表示
我们已经学过一个正数的算术平方根的表示方法,你能表示一个非负数的平方根吗?
非负数a的算术平方根 ;(正号一般省略)
非负数a的负的平方根 ;
非负数a的平方根 , 读作:正、负根号a
求平方根的写法如下:
如9的平方根,可记作:
5 的平方根,可以记作 和- ,或±
注意:因为负数没有平方根,所以在式子
中的被开方数 a ≥0 ,否则式子 没有意义。
即式子 中的 a 是一个非负数。
