《志鸿全优设计》2013-2014学年高中数学湘教版必修2单元检测:第5章 三角恒等变换(含答案)
文档属性
| 名称 | 《志鸿全优设计》2013-2014学年高中数学湘教版必修2单元检测:第5章 三角恒等变换(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 904.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
数学湘教版必修2第5章 三角恒等变换单元检测
(时间:45分钟 满分:100分)
一、选择题(每小题5分,共40分)
1.(2011北京高一期末检测)已知角α的终边经过点P(1, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ),则cos 2α的值为( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
2.(2011重庆南开中学高一检测)设θ∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则cos θ-sin θ的值是( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
3.(原创题)函数f(x)=sin2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1的最小正周期为( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C.π D.2π
4.(2011浙江高考,理6)若0<α< HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <β<0, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
5.(2012重庆高考,理5)设tan α,tan β是方程x2-3x+2=0的两根,则tan(α+β)的值为( )www.21-cn-jy.com
A.-3 B.-1 C.1 D.3
6.函数y=sin 2x-2cos2x的最大值是 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B.1
C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D.3
7.(2011浙江宁波高一期中检测)若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 等于( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
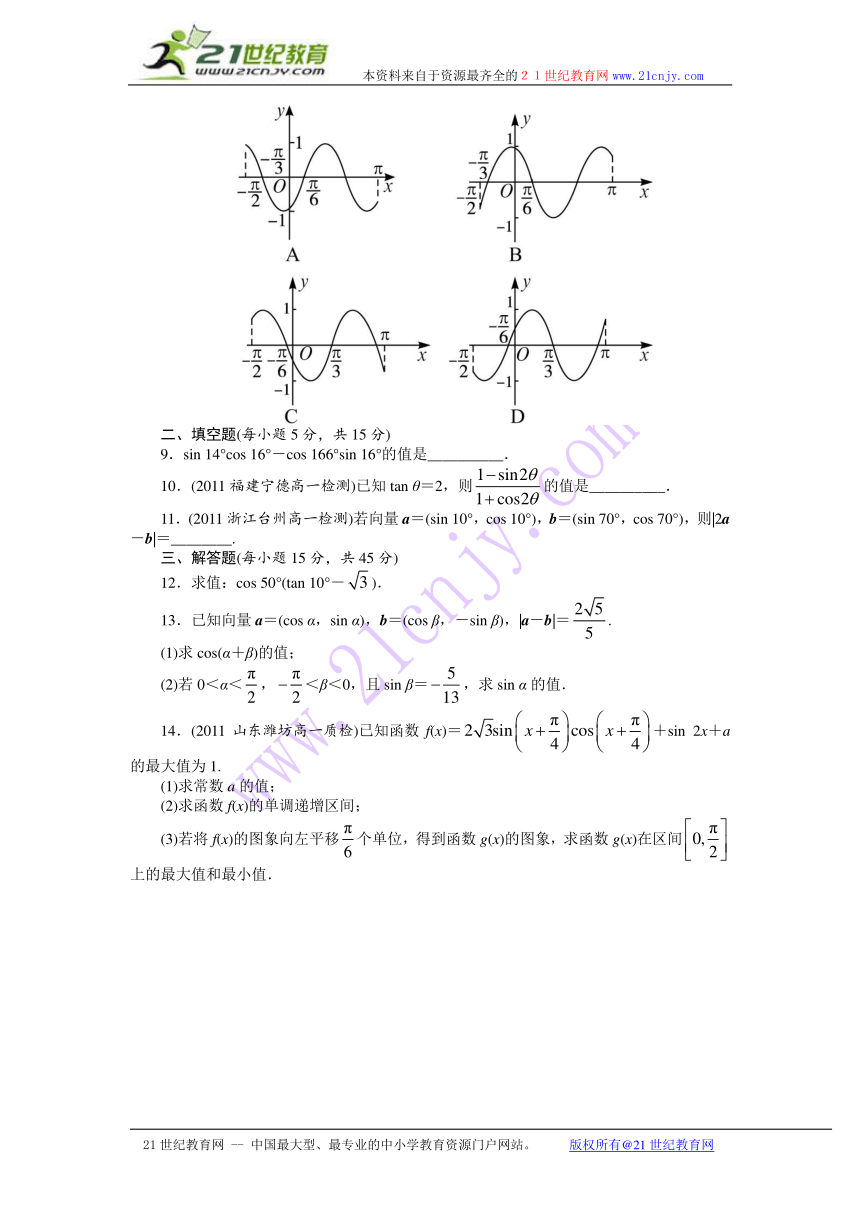
8.(2011辽宁沈阳高一检测)函数y=cos x(sin x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 cos x)+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在区间 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的简图是( )21cnjy.com
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "../../../g02.EPS" \* MERGEFORMAT
二、填空题(每小题5分,共15分)
9.sin 14°cos 16°-cos 166°sin 16°的值是__________.
10.(2011福建宁德高一检测)已知tan θ=2,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值是__________.
11.(2011浙江台州高一检测)若向量a=(sin 10°,cos 10°),b=(sin 70°,cos 70°),则|2a-b|=________.21·cn·jy·com
三、解答题(每小题15分,共45分)
12.求值:cos 50°(tan 10°- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ).
13.已知向量a=(cos α,sin α),b=(cos β,-sin β),|a-b|= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
(1)求cos(α+β)的值;
(2)若0<α< HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <β<0,且sin β= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,求sin α的值.
14.(2011山东潍坊高一质检)已知函数f(x)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 +sin 2x+a的最大值为1.
(1)求常数a的值;
(2)求函数f(x)的单调递增区间;
(3)若将f(x)的图象向左平移 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 个单位,得到函数g(x)的图象,求函数g(x)在区间 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的最大值和最小值.2·1·c·n·j·y
参考答案
1. 答案:A
解析:依题意知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以cos 2α=2cos2α-1=2· HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
2. 答案:D
解析:由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得sin 2θ= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
于是(cos θ-sin θ)2=1-sin 2θ= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
而θ∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以cos θ<sin θ,于是cos θ-sin θ= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
3. 答案:B
解析:由于f(x)=sin2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 sin 4x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以最小正周期为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
4. 答案:C
解析:根据条件可得α+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
5. 答案:A
解析:因为tan α,tan β是方程x2-3x+2=0的两根,所以tan α+tan β=3,tan α·tan β=2,而tan(α+β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =-3,故选A.21世纪教育网版权所有
6. 答案:A
解析:函数y=sin 2x-2cos2x=sin 2x-cos 2x-1
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以函数y=sin 2x-2cos2x的最大值是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
7. 答案:A
解析:由于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
于是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1=2· HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
8. 答案:A
解析:由于y=cos x(sin x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 cos x)+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
=cos xsin x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 cos2x+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
又因为x∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,故简图是A.
9. 答案:
解析:sin 14°cos 16°-cos 166°sin 16°=sin 14°cos 16°+cos 14°sin 16°=sin(14°+16°)=sin 30°= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .21教育网
10. 答案: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
解析: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 [21世纪教育网
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
11. 答案: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 21世纪教育网
解析:|2a-b|= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
12.解:cos 50°(tan 10°- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )=cos 50° HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
13. 解:(1)|a|2-2a·b+|b|2= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
2-2(cos αcos β-sin αsin β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴cos(α+β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .[21世纪教育网]
(2)∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <β<0,且sin β= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴cos β= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <β<0.[来源:21世纪教育网]
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <α+β< HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
又∵cos(α+β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴0<α+β< HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴sin(α+β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴sin α=sin [(α+β)-β]
=sin(α+β)cos β-cos(α+β)sin β
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
14. 解:(1)∵f(x)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 +sin 2x+a
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 cos 2x+sin 2x+a=2sin HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 +a≤1,
∴2+a=1,∴a=-1.
(2)由(1)知f(x)=2sin HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1,
令2kπ- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤2x+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤2kπ+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
解得kπ- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤x≤kπ+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴函数f(x)的单调递增区间为
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (k∈Z).
(3)∵将f(x)的图象向左平移 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 个单位,得到函数g(x)的图象,
∴g(x)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -121世纪教育网
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∵x∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴2x+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,即当x=0时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,g(x)取得最大值 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,即当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,g(x)取得最小值-3.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
数学湘教版必修2第5章 三角恒等变换单元检测
(时间:45分钟 满分:100分)
一、选择题(每小题5分,共40分)
1.(2011北京高一期末检测)已知角α的终边经过点P(1, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ),则cos 2α的值为( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
2.(2011重庆南开中学高一检测)设θ∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则cos θ-sin θ的值是( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
3.(原创题)函数f(x)=sin2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1的最小正周期为( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C.π D.2π
4.(2011浙江高考,理6)若0<α< HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <β<0, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
5.(2012重庆高考,理5)设tan α,tan β是方程x2-3x+2=0的两根,则tan(α+β)的值为( )www.21-cn-jy.com
A.-3 B.-1 C.1 D.3
6.函数y=sin 2x-2cos2x的最大值是 ( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B.1
C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D.3
7.(2011浙江宁波高一期中检测)若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 等于( )
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
8.(2011辽宁沈阳高一检测)函数y=cos x(sin x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 cos x)+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在区间 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的简图是( )21cnjy.com
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "../../../g02.EPS" \* MERGEFORMAT
二、填空题(每小题5分,共15分)
9.sin 14°cos 16°-cos 166°sin 16°的值是__________.
10.(2011福建宁德高一检测)已知tan θ=2,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值是__________.
11.(2011浙江台州高一检测)若向量a=(sin 10°,cos 10°),b=(sin 70°,cos 70°),则|2a-b|=________.21·cn·jy·com
三、解答题(每小题15分,共45分)
12.求值:cos 50°(tan 10°- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ).
13.已知向量a=(cos α,sin α),b=(cos β,-sin β),|a-b|= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
(1)求cos(α+β)的值;
(2)若0<α< HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <β<0,且sin β= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,求sin α的值.
14.(2011山东潍坊高一质检)已知函数f(x)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 +sin 2x+a的最大值为1.
(1)求常数a的值;
(2)求函数f(x)的单调递增区间;
(3)若将f(x)的图象向左平移 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 个单位,得到函数g(x)的图象,求函数g(x)在区间 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的最大值和最小值.2·1·c·n·j·y
参考答案
1. 答案:A
解析:依题意知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以cos 2α=2cos2α-1=2· HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
2. 答案:D
解析:由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得sin 2θ= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
于是(cos θ-sin θ)2=1-sin 2θ= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
而θ∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以cos θ<sin θ,于是cos θ-sin θ= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
3. 答案:B
解析:由于f(x)=sin2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 sin 4x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以最小正周期为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
4. 答案:C
解析:根据条件可得α+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
5. 答案:A
解析:因为tan α,tan β是方程x2-3x+2=0的两根,所以tan α+tan β=3,tan α·tan β=2,而tan(α+β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =-3,故选A.21世纪教育网版权所有
6. 答案:A
解析:函数y=sin 2x-2cos2x=sin 2x-cos 2x-1
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以函数y=sin 2x-2cos2x的最大值是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
7. 答案:A
解析:由于 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
于是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1=2· HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
8. 答案:A
解析:由于y=cos x(sin x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 cos x)+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
=cos xsin x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 cos2x+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
又因为x∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,故简图是A.
9. 答案:
解析:sin 14°cos 16°-cos 166°sin 16°=sin 14°cos 16°+cos 14°sin 16°=sin(14°+16°)=sin 30°= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .21教育网
10. 答案: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
解析: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 [21世纪教育网
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
11. 答案: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 21世纪教育网
解析:|2a-b|= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
12.解:cos 50°(tan 10°- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )=cos 50° HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
13. 解:(1)|a|2-2a·b+|b|2= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
2-2(cos αcos β-sin αsin β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴cos(α+β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .[21世纪教育网]
(2)∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <β<0,且sin β= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴cos β= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <β<0.[来源:21世纪教育网]
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <α+β< HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
又∵cos(α+β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴0<α+β< HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴sin(α+β)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴sin α=sin [(α+β)-β]
=sin(α+β)cos β-cos(α+β)sin β
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
14. 解:(1)∵f(x)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 +sin 2x+a
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 cos 2x+sin 2x+a=2sin HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 +a≤1,
∴2+a=1,∴a=-1.
(2)由(1)知f(x)=2sin HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1,
令2kπ- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤2x+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤2kπ+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
解得kπ- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ≤x≤kπ+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴函数f(x)的单调递增区间为
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (k∈Z).
(3)∵将f(x)的图象向左平移 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 个单位,得到函数g(x)的图象,
∴g(x)= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -121世纪教育网
= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∵x∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴2x+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,即当x=0时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,g(x)取得最大值 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,即当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,g(x)取得最小值-3.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
