《志鸿全优设计》2013-2014学年高中数学湘教版必修3单元检测:第7章解析几何初步(含答案)
文档属性
| 名称 | 《志鸿全优设计》2013-2014学年高中数学湘教版必修3单元检测:第7章解析几何初步(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 08:35:54 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
数学湘教版必修3第7章解析几何初步单元检测
(时间60分钟,满分100分)
一、选择题(每小题6分,共48分)
1方程y=k(x-1)(k∈R)表示( ).
A.过点(-1,0)的一切直线
B.过点(1,0)的一切直线
C.过点(1,0)且不垂直于x轴的一切直线
D.过点(1,0)且除x轴外的一切直线
2若x2+y2-2x+y+m=0表示一个圆的方程,则实数m的取值范围是( ).
A.m<5 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
3设圆心为C1的方程为(x-5)2+(y-3)2=9,圆心为C2的方程为x2+y2-4x+2y-9=0,则两圆的圆心距等于( ).21·cn·jy·com
A.5 B.25 C.10 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
4平行于直线2x-y+1=0且与圆x2+y2=5相切的直线的方程是( ).
A.2x-y+5=0
B.2x-y-5=0
C.2x+y+5=0或2x+y-5=0
D.2x-y+5=0或2x-y-5=0
5如果直线mx+3y-1=0与直线x-y+5=0互相垂直,那么m的值等于( ).
A.-3 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C.3 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
6直线2x+3y-6=0关于点(1,-1)对称的直线方程是( ).
A.3x-2y+2=0 B.2x+3y+7=0
C.3x-2y-12=0 D.2x+3y+8=0
7若直线2ax-by+2=0(a,b∈R)始终平分圆x2+y2+2x-4y+1=0的圆周,则ab的取值范围是( ).21世纪教育网版权所有
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
8若不等式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的解集为{x|0<x≤4},则实数a的取值范围是( ).
A.a≥0 B.a<4 C.a<0 D.a≤0
二、填空题(每小题6分,共18分)
9与圆x2+(y+5)2=3相切,且纵横截距相等的直线共有________条.
10若点A(2,1,4)与点P(x,y,z)的距离为5,则x,y,z满足的关系式是________.
11若直线ax+y=1与圆(x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )2+(y-2)2=1有两个不同的交点,则a的取值范围是__________.【来源:21·世纪·教育·网】
三、解答题(共34分)
12(10分)已知圆过点A(-2,4),半径为5,并且以M(-1,3)为中点的弦长为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求该圆的方程.2-1-c-n-j-y
13(10分)已知直线l经过两条直线l1:3x+4y-2=0与l2:2x+y+2=0的交点P,
(1)求垂直于直线l3:x-2y-1=0的直线l的方程.
(2)求与坐标轴相交于两点,且以P为中点的直线方程.
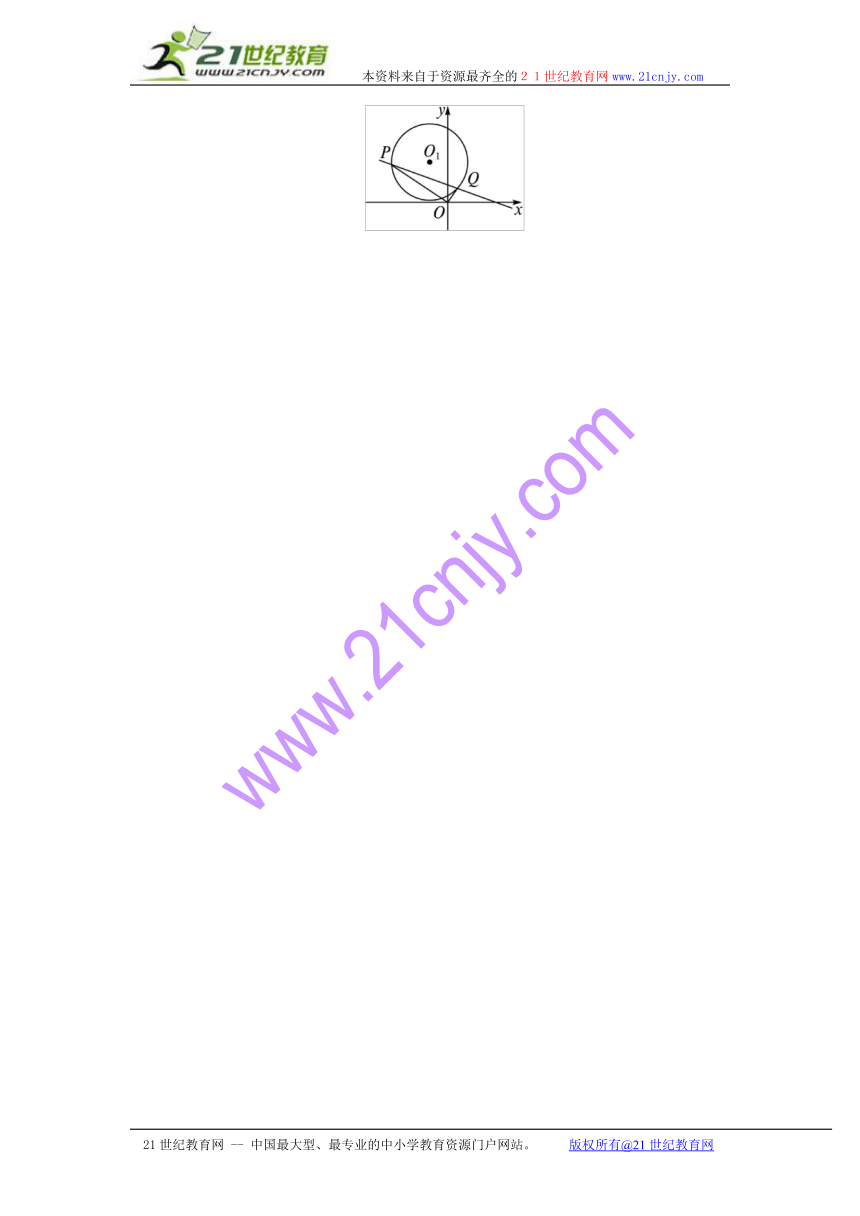
14(14分)如图,若圆x2+y2+x-6y+c=0与直线x+2y-3=0的两个交点分别为P,Q,O为坐标原点,满足OP⊥OQ,求c的值.21教育网
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "../../../B39.EPS" \* MERGEFORMAT
参考答案
1. 解析:y-y0=k(x-x0)表示过(x0,y0)且斜率存在的直线.
答案:C
2. 解析:∵x2+y2-2x+y+m=0表示一个圆的方程,21世纪教育网
∴ (-2)2+12-4m>0.∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
答案:B
3. 解析:圆C1的圆心坐标为(5,3),圆C2的圆心坐标为(2,-1).
两圆圆心距|C1C2|= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =5,即两圆的圆心距等于5.
答案:A
4. 解析:设所求直线方程为2x-y+c=0,则由题意得
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴c=±5.
答案:D
5. 解析:显然两条直线的斜率都存在,当斜率乘积等于-1时,两直线垂直,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ×1=-1,∴m=3.
答案:C
6. 解析:直线关于点的对称直线一定与原 ( http: / / www.21cnjy.com )直线平行,所以排除A、C.在2x+3y-6=0上取一点(3,0),它关于(1,-1)的对称点是(-1,-2),此点在直线2x+3y+8=0上.
答案:D
7. 解析:∵圆的方程是x2+y2+2x-4y+1=0,
∴圆心坐标为(-1,2).
∵直线2ax-by+2=0(a,b∈R)始终平分圆周,
∴圆心在直线2ax-by+2=0上.
∴-2a-2b+2=0.∴a+b=1.
∴ab=a(1-a)=-a2+a= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴ab∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
答案:A
8. 解析:如下图,令,g(x)=ax,则f(x)的图象是以(2,0)为圆心,以2为半径的圆在x轴的上半部分;y=g(x)的图象是过原点的一条直线,欲使原不等式的解集为{x|0<x≤4},即在区间(0,4]上,y=f(x)的图象在y=g(x)的图象的上方,必有g(x)=ax的斜率小于0,∴a<0.21cnjy.com
( http: / / www.21cnjy.com )
答案:C
9. 解析:如图,当直线过原点时,纵横截距相等且均为0.这样的直线有2条,当直线不过原点时,要使纵横截距相等,需斜率k=-1,这样的直线也有2条,故共有4条满足条件的直线.21世纪教育网www.21-cn-jy.com
( http: / / www.21cnjy.com )
答案:421世纪教育网
10. 解析:∵|PA|=5,A(2,1,4),P(x,y,z),
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴(x-2)2+(y-1)2+(z-4)2=25.
答案:(x-2)2+(y-1)2+(z-4)2=25
11. 解析:直线ax+y=1与圆(x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )2+(y-2)2=1有两个不同的交点,即方程(x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )2+(-ax+1-2)2=1有两个不等的实根,即(1+a2)x2+2(a- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )x+3=0的判别式Δ>0,也即4(a- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )2-4×3(1+a2)>0,解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <a<0.2·1·c·n·j·y
答案: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <a<021世纪教育网
12.解:设所求圆的方程为(x-a)2+(y-b)2=25.根据题设,知(a+2)2+(b-4)2=25,(a+1)2+(b-3)2+12=25,联立以上两个方程,解得a=2,b=1或a=1,b=0.故所求圆的方程为(x-2)2+(y-1)2=25或(x-1)2+y2=25.21·世纪*教育网
13. 解:(1)由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
∴点P的坐标是(-2,2).
∵所求直线l与l3垂直,
∴设直线l的方程为2x+y+C=0.把点P的坐标代入得2×(-2)+2+C=0,得C=2.
∴所求直线l的方程为2x+y+2=0.
(2)设与x轴交于A(a,0),与y轴交于B(0,b),
∵点P(-2,2)为中点,∴a=-4,b=4,直线方程l为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即x-y+4=0.
14. 解法一:设M点是弦PQ的中点,由O1M⊥PQ,O1 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,可求直线O1M的方程,再联立直线PQ方程可解交点M(-1,2),再设圆M的方程为(x+1)2+(y-2)2=r2.
( http: / / www.21cnjy.com )
因为OP⊥OQ,则圆M过原点,可得圆M的方程x2+y2+2x-4y=0,再将该圆方程与已知圆方程相减便得弦PQ的方程:x+2y-c=0,又由PQ:x+2y-3=0,可得c=3.
解法二:根据圆的性质利用几何知识求.21世纪教育网
已知圆的半径 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,同解法一可求出M(-1,2),由△PQO为直角三角形得|PM|=|MO|= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
又由点O1到直线PQ的距离 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,在Rt△PMO1中,|O1M|2+|PM|2=|O1P|2=R2,由此可得c=3.www-2-1-cnjy-com
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
数学湘教版必修3第7章解析几何初步单元检测
(时间60分钟,满分100分)
一、选择题(每小题6分,共48分)
1方程y=k(x-1)(k∈R)表示( ).
A.过点(-1,0)的一切直线
B.过点(1,0)的一切直线
C.过点(1,0)且不垂直于x轴的一切直线
D.过点(1,0)且除x轴外的一切直线
2若x2+y2-2x+y+m=0表示一个圆的方程,则实数m的取值范围是( ).
A.m<5 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
3设圆心为C1的方程为(x-5)2+(y-3)2=9,圆心为C2的方程为x2+y2-4x+2y-9=0,则两圆的圆心距等于( ).21·cn·jy·com
A.5 B.25 C.10 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
4平行于直线2x-y+1=0且与圆x2+y2=5相切的直线的方程是( ).
A.2x-y+5=0
B.2x-y-5=0
C.2x+y+5=0或2x+y-5=0
D.2x-y+5=0或2x-y-5=0
5如果直线mx+3y-1=0与直线x-y+5=0互相垂直,那么m的值等于( ).
A.-3 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C.3 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
6直线2x+3y-6=0关于点(1,-1)对称的直线方程是( ).
A.3x-2y+2=0 B.2x+3y+7=0
C.3x-2y-12=0 D.2x+3y+8=0
7若直线2ax-by+2=0(a,b∈R)始终平分圆x2+y2+2x-4y+1=0的圆周,则ab的取值范围是( ).21世纪教育网版权所有
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
8若不等式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的解集为{x|0<x≤4},则实数a的取值范围是( ).
A.a≥0 B.a<4 C.a<0 D.a≤0
二、填空题(每小题6分,共18分)
9与圆x2+(y+5)2=3相切,且纵横截距相等的直线共有________条.
10若点A(2,1,4)与点P(x,y,z)的距离为5,则x,y,z满足的关系式是________.
11若直线ax+y=1与圆(x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )2+(y-2)2=1有两个不同的交点,则a的取值范围是__________.【来源:21·世纪·教育·网】
三、解答题(共34分)
12(10分)已知圆过点A(-2,4),半径为5,并且以M(-1,3)为中点的弦长为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,试求该圆的方程.2-1-c-n-j-y
13(10分)已知直线l经过两条直线l1:3x+4y-2=0与l2:2x+y+2=0的交点P,
(1)求垂直于直线l3:x-2y-1=0的直线l的方程.
(2)求与坐标轴相交于两点,且以P为中点的直线方程.
14(14分)如图,若圆x2+y2+x-6y+c=0与直线x+2y-3=0的两个交点分别为P,Q,O为坐标原点,满足OP⊥OQ,求c的值.21教育网
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "../../../B39.EPS" \* MERGEFORMAT
参考答案
1. 解析:y-y0=k(x-x0)表示过(x0,y0)且斜率存在的直线.
答案:C
2. 解析:∵x2+y2-2x+y+m=0表示一个圆的方程,21世纪教育网
∴ (-2)2+12-4m>0.∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
答案:B
3. 解析:圆C1的圆心坐标为(5,3),圆C2的圆心坐标为(2,-1).
两圆圆心距|C1C2|= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =5,即两圆的圆心距等于5.
答案:A
4. 解析:设所求直线方程为2x-y+c=0,则由题意得
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴c=±5.
答案:D
5. 解析:显然两条直线的斜率都存在,当斜率乘积等于-1时,两直线垂直,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ×1=-1,∴m=3.
答案:C
6. 解析:直线关于点的对称直线一定与原 ( http: / / www.21cnjy.com )直线平行,所以排除A、C.在2x+3y-6=0上取一点(3,0),它关于(1,-1)的对称点是(-1,-2),此点在直线2x+3y+8=0上.
答案:D
7. 解析:∵圆的方程是x2+y2+2x-4y+1=0,
∴圆心坐标为(-1,2).
∵直线2ax-by+2=0(a,b∈R)始终平分圆周,
∴圆心在直线2ax-by+2=0上.
∴-2a-2b+2=0.∴a+b=1.
∴ab=a(1-a)=-a2+a= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴ab∈ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
答案:A
8. 解析:如下图,令,g(x)=ax,则f(x)的图象是以(2,0)为圆心,以2为半径的圆在x轴的上半部分;y=g(x)的图象是过原点的一条直线,欲使原不等式的解集为{x|0<x≤4},即在区间(0,4]上,y=f(x)的图象在y=g(x)的图象的上方,必有g(x)=ax的斜率小于0,∴a<0.21cnjy.com
( http: / / www.21cnjy.com )
答案:C
9. 解析:如图,当直线过原点时,纵横截距相等且均为0.这样的直线有2条,当直线不过原点时,要使纵横截距相等,需斜率k=-1,这样的直线也有2条,故共有4条满足条件的直线.21世纪教育网www.21-cn-jy.com
( http: / / www.21cnjy.com )
答案:421世纪教育网
10. 解析:∵|PA|=5,A(2,1,4),P(x,y,z),
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴(x-2)2+(y-1)2+(z-4)2=25.
答案:(x-2)2+(y-1)2+(z-4)2=25
11. 解析:直线ax+y=1与圆(x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )2+(y-2)2=1有两个不同的交点,即方程(x- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )2+(-ax+1-2)2=1有两个不等的实根,即(1+a2)x2+2(a- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )x+3=0的判别式Δ>0,也即4(a- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )2-4×3(1+a2)>0,解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <a<0.2·1·c·n·j·y
答案: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <a<021世纪教育网
12.解:设所求圆的方程为(x-a)2+(y-b)2=25.根据题设,知(a+2)2+(b-4)2=25,(a+1)2+(b-3)2+12=25,联立以上两个方程,解得a=2,b=1或a=1,b=0.故所求圆的方程为(x-2)2+(y-1)2=25或(x-1)2+y2=25.21·世纪*教育网
13. 解:(1)由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
∴点P的坐标是(-2,2).
∵所求直线l与l3垂直,
∴设直线l的方程为2x+y+C=0.把点P的坐标代入得2×(-2)+2+C=0,得C=2.
∴所求直线l的方程为2x+y+2=0.
(2)设与x轴交于A(a,0),与y轴交于B(0,b),
∵点P(-2,2)为中点,∴a=-4,b=4,直线方程l为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即x-y+4=0.
14. 解法一:设M点是弦PQ的中点,由O1M⊥PQ,O1 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,可求直线O1M的方程,再联立直线PQ方程可解交点M(-1,2),再设圆M的方程为(x+1)2+(y-2)2=r2.
( http: / / www.21cnjy.com )
因为OP⊥OQ,则圆M过原点,可得圆M的方程x2+y2+2x-4y=0,再将该圆方程与已知圆方程相减便得弦PQ的方程:x+2y-c=0,又由PQ:x+2y-3=0,可得c=3.
解法二:根据圆的性质利用几何知识求.21世纪教育网
已知圆的半径 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,同解法一可求出M(-1,2),由△PQO为直角三角形得|PM|=|MO|= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
又由点O1到直线PQ的距离 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,在Rt△PMO1中,|O1M|2+|PM|2=|O1P|2=R2,由此可得c=3.www-2-1-cnjy-com
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
