人教版数学七年级下册《第6章 实数》2023年单元练习(含解析)
文档属性
| 名称 | 人教版数学七年级下册《第6章 实数》2023年单元练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 62.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 08:25:34 | ||
图片预览



文档简介
人教版七年级下册《第6章 实数》2023年单元测试
一 、单选题
1.下列说法中,正确的有
①万精确到百位;
②有理数和数轴上的点一一对应;
③在,,,,,中,无理数有个;
④是一个一次二项式,它的两项分别是和
A. 个 B. 个 C. 个 D. 个
2.在,,,,,…每两个之间依次多一个中,无理数的个数是
A. 个 B. 个 C. 个 D. 个
3.估计 的值在( ).
A. 1与2之间 B. 2与3之间 C. 3与4之间 D. 4与5之间
4.如图为某同学完成的作业,他做对的题数是
填空: ①的倒数是; ②; ③,,,,的中位数是; ④,,,的众数是; ⑤; ⑥
A. 个 B. 个 C. 个 D. 个
5.下列语句正确的个数是( )①直角三角形只有一条高;
②钝角三角形只有一条高在三角形内部;
③三角形三条高相交于一点,这点不在三角形内,就在三角形外;④三条中线、三条角平分线都在三角形内部。
A. 1 B. 2 C. 3 D. 4
6.实数在数轴上的位置,如图所示,那么化简的结果是 .
A. B. C. D.
7.在,,,四个数中,最小的数是
A. B. C. D.
二 、填空题
8.比较大小:______填、或
9.的算术平方根是 ______,的平方根是 ______.
10.在学习实数内容时,我们通过“逐步逼近”的方法可以计算出的近似值,得出利用“逐步逼近”法,请回答下列问题:
介于连续的两个整数和之间,且,那么________,________;
若是的小数部分,是的整数部分,求的平方根.
11.计算:______.
12.已知,表示下表中两个相邻的数,且,则______.
三 、解答题
13.计算:
14.已知,是的平方根,且,求的值.
15.计算:.
16.已知一个正数的两个不同平方根是与.
求的值;
求关于的方程的解.
17.气象资料表明:某地雷雨持续的时间可以用下面的公式来估计:,其中是雷雨区域的直径.
如果雷雨区域的直径为,那么这场雷雨大约能持续多长时间?
如果一场雷雨持续了,那么这场雷雨区域的直径大约是多少?
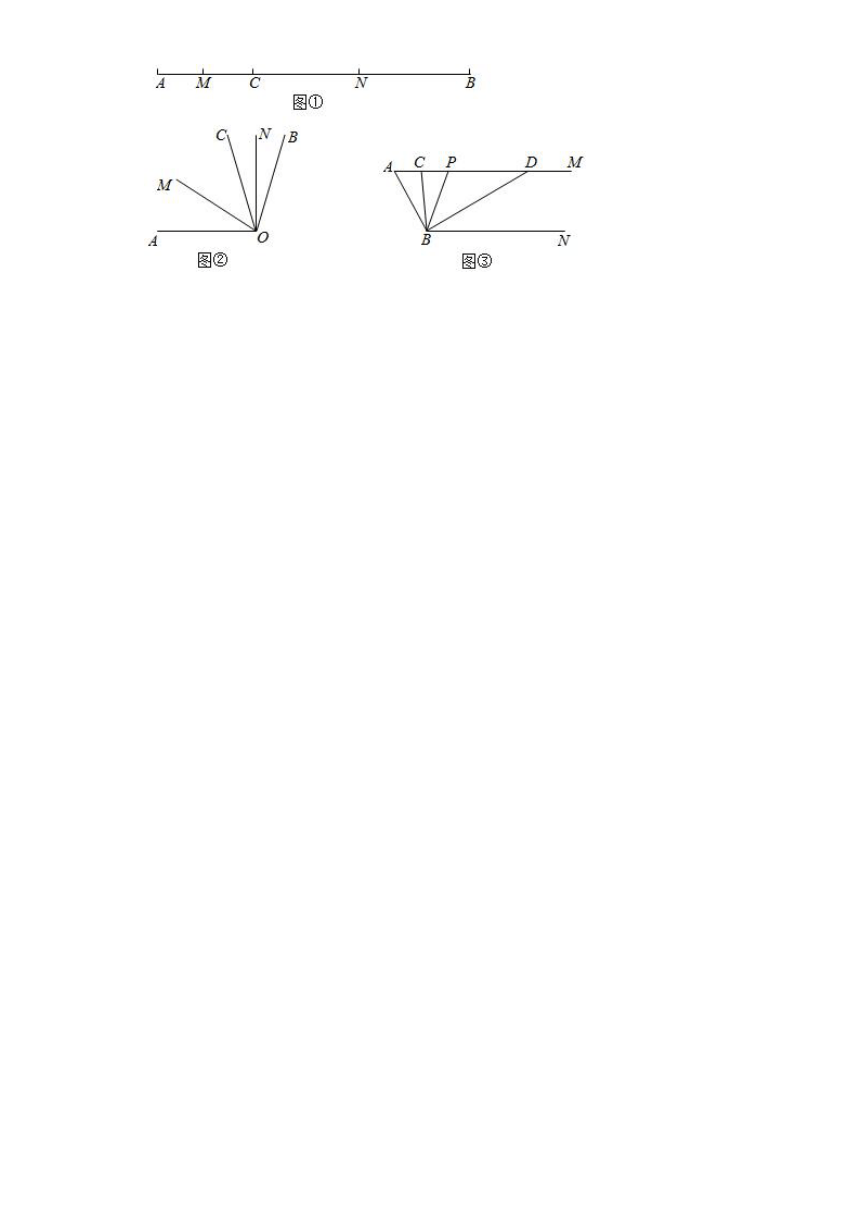
18.【问题】如图①线段,点是线段上一动点,点、分别是线段、的中点,求线段的长请写出说理步骤
【拓展】如图①,线段点是线段上一动点,点从分别是线段、的中点,则线段的长为 ______ 用含字母的代数式表示
【应用】如图②,,射线是内部任一射线,射线、分别平分、,则的大小为 ______ 用含字母的代数式表示;
如图③,,,点是射线上一动点与点不重合,、分别平分、,分别交射线于点,求与的差.
答案和解析
1.【答案】B;
【解析】解:①万精确到百位,原说法是正确的;
②实数与数轴上的点一一对应,原来的说法错误;
③在,,,,,中,无理数有,,一共个,原说法是正确的;
④是一个一次二项式,它的两项分别是和,原来的说法错误.
故选:
根据近似数,无理数的概念,实数与数轴的关系,多项式的定义,对各选项分析判断后利用排除法求解.
此题主要考查了近似数,无理数的概念,实数与数轴的关系,多项式,是基本概念题,熟记概念是解答该题的关键.
2.【答案】B;
【解析】解:,是有限小数,属于有理数;
是整数,属于有理数;
是分数,属于有理数;
无理数有,…每两个之间依次多一个,共个.
故选:
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
此题主要考查了无理数的定义,其中初中范围内学习的无理数有:,等;开方开不尽的数;以及像…,等有这样规律的数.
3.【答案】C;
【解析】略
4.【答案】D;
【解析】解:①的倒数是,正确;
②,正确;
③,,,,的中位数是,原结论错误;
④,,,的众数是,原结论错误;
⑤,正确;
⑥,原结论错误.
所以他做对的题数是个.
故选:
①根据倒数的定义判断即可;②根据绝对值的定义判断即可;③根据中位数的定义判断即可;④根据众数的定义判断即可;⑤根据立方根的定义判断即可;⑥根据算术平方根的定义判断即可.
此题主要考查了众数,中位数,绝对值,立方根以及算术平方根,掌握相关定义是解答本题的关键.
5.【答案】B;
【解析】任何三角形都有三条高,它们相交于一点,
锐角三角形三条高的交点在形内,直角三角形三条高的交点就是直角顶点,钝角三角形只有一条高在形内,三条高的交点在形外,
而三角形的三条中线,三条角平分线都在三角形内部,
所以①③错误,②④正确。故答案为:B。
6.【答案】A;
【解析】
【分析】
本题主要考查了二次根式和绝对值的性质与化简.特别因为都是数轴上的实数,注意符号的变换.根据二次根式和绝对值的性质,化简解答. 【解答】解:由数轴可得,,根据二次根式和绝对值的性质,化简得,
,
,
.
故选A.
7.【答案】A;
【解析】解:,
最小的数是,
故选:
先根据实数的大小比较法则比较数的大小,再得出答案即可.
此题主要考查了实数的大小比较和算术平方根,能根据实数的大小比较法则比较数的大小是解此题的关键,注意:正数都大于,负数都小于,正数大于一切负数,两个负数比较大小,其绝对值大的反而小.
8.【答案】<;
【解析】解:,则,
,
故答案为:
根据,则,再判断负数即可.
此题主要考查实数大小比较,熟练根据正数的大小比较其相反数大小是解答该题的关键.
9.【答案】 ±2;
【解析】解:的算术平方根是,,的平方根是
故答案为:,
根据算术平方根、平方根的定义解答.
此题主要考查平方根和算术平方根,熟练掌握平方根和算术平方根的定义是解题关键.
10.【答案】,;
,
的平方根是;
【解析】
由介于和两个平方数之间,即可求得和的值;
由“逐步逼近”法知,可求得、的值,带入即可求得结果.
解:,
,即,
故答案为:,;
见答案.
11.【答案】-13;
【解析】解:原式
故答案为:
直接利用立方根的性质以及有理数的乘方运算法则分别化简,进而得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
12.【答案】17.6;
【解析】解:,是表中两个相邻的数,,
,
故答案为:
根据表中的数据进行解答即可.
此题主要考查估算无理数的大小,解答该题的关键是掌握算术平方根的定义.
13.【答案】;
【解析】
先把算式进行整理,再进行计算求解;
先计算平方、绝对值和算术平方根,再计算加减.
此题主要考查了实数混合运算的能力,关键是能准确确定计算顺序,并能进行正确地计算.
14.【答案】解:由题意得,x=±,y=±,
∵|y-x|=x-y,
∴x>y
∴x=,y=或x=,y=-.
∴x+y=+或x+y=-.;
【解析】
先依据绝对值和平方根的定义确定出、的值,然后依据绝对值的性质求得、可能的情况,最后进行计算即可.
这道题主要考查的是实数的性质、平方根的性质,分类讨论是解答该题的关键.
15.【答案】解:原式=,
=.;
【解析】【分析】
通过计算零指数幂、负指数幂、分母有理化、开平方的计算即可得出结论;
【点睛】本题主要考查了实数的计算,计算正确是解题的关键.
16.【答案】解:由题意得,,
解得,;
,
,
.;
【解析】、根据一个正数有两个平方根,这两个平方根互为相反数解答.
该题考查的是平方根的概念,掌握一个正数有两个平方根,这两个平方根互为相反数是解答该题的关键,
17.【答案】
解:根据,,
则,
答:这场雷雨大约能持续;
根据,其中,
答:这场雷雨区域的直径大约是;
【解析】
此题主要考查了算术平方根的应用,注意一个正数的算术平方根只有一个.
根据,其中是雷雨区域的直径,开平方的意义,可得答案;
根据,其中是雷雨区域的直径,开平方的意义,可得答案.
18.【答案】 ;
【解析】解:【问题】、分别是线段、的中点,
,,
;
【拓展】、分别是线段、的中点,
,,
故答案为:;
射线、分别平分、,
,,
故答案为:;
,,
,
又、分别平分、,
由结论可知,
,
,
,
与的差为
【问题】由点、分别是线段、的中点,可得,,因为,代入计算即可得出答案;
【拓展】解法同【问题】;
【应用】由射线、分别平分、,可得,,因为,代入即可得出答案;
根据平行线的性质可得,再根据中的结论可得出的度数,再根据三角形的外角定理,即可得出答案.
此题主要考查了平行线的性质,角平分线的性质及线段的中点,熟练掌握角平分线的性质和平行线的性质是解决本题的关键.
一 、单选题
1.下列说法中,正确的有
①万精确到百位;
②有理数和数轴上的点一一对应;
③在,,,,,中,无理数有个;
④是一个一次二项式,它的两项分别是和
A. 个 B. 个 C. 个 D. 个
2.在,,,,,…每两个之间依次多一个中,无理数的个数是
A. 个 B. 个 C. 个 D. 个
3.估计 的值在( ).
A. 1与2之间 B. 2与3之间 C. 3与4之间 D. 4与5之间
4.如图为某同学完成的作业,他做对的题数是
填空: ①的倒数是; ②; ③,,,,的中位数是; ④,,,的众数是; ⑤; ⑥
A. 个 B. 个 C. 个 D. 个
5.下列语句正确的个数是( )①直角三角形只有一条高;
②钝角三角形只有一条高在三角形内部;
③三角形三条高相交于一点,这点不在三角形内,就在三角形外;④三条中线、三条角平分线都在三角形内部。
A. 1 B. 2 C. 3 D. 4
6.实数在数轴上的位置,如图所示,那么化简的结果是 .
A. B. C. D.
7.在,,,四个数中,最小的数是
A. B. C. D.
二 、填空题
8.比较大小:______填、或
9.的算术平方根是 ______,的平方根是 ______.
10.在学习实数内容时,我们通过“逐步逼近”的方法可以计算出的近似值,得出利用“逐步逼近”法,请回答下列问题:
介于连续的两个整数和之间,且,那么________,________;
若是的小数部分,是的整数部分,求的平方根.
11.计算:______.
12.已知,表示下表中两个相邻的数,且,则______.
三 、解答题
13.计算:
14.已知,是的平方根,且,求的值.
15.计算:.
16.已知一个正数的两个不同平方根是与.
求的值;
求关于的方程的解.
17.气象资料表明:某地雷雨持续的时间可以用下面的公式来估计:,其中是雷雨区域的直径.
如果雷雨区域的直径为,那么这场雷雨大约能持续多长时间?
如果一场雷雨持续了,那么这场雷雨区域的直径大约是多少?
18.【问题】如图①线段,点是线段上一动点,点、分别是线段、的中点,求线段的长请写出说理步骤
【拓展】如图①,线段点是线段上一动点,点从分别是线段、的中点,则线段的长为 ______ 用含字母的代数式表示
【应用】如图②,,射线是内部任一射线,射线、分别平分、,则的大小为 ______ 用含字母的代数式表示;
如图③,,,点是射线上一动点与点不重合,、分别平分、,分别交射线于点,求与的差.
答案和解析
1.【答案】B;
【解析】解:①万精确到百位,原说法是正确的;
②实数与数轴上的点一一对应,原来的说法错误;
③在,,,,,中,无理数有,,一共个,原说法是正确的;
④是一个一次二项式,它的两项分别是和,原来的说法错误.
故选:
根据近似数,无理数的概念,实数与数轴的关系,多项式的定义,对各选项分析判断后利用排除法求解.
此题主要考查了近似数,无理数的概念,实数与数轴的关系,多项式,是基本概念题,熟记概念是解答该题的关键.
2.【答案】B;
【解析】解:,是有限小数,属于有理数;
是整数,属于有理数;
是分数,属于有理数;
无理数有,…每两个之间依次多一个,共个.
故选:
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
此题主要考查了无理数的定义,其中初中范围内学习的无理数有:,等;开方开不尽的数;以及像…,等有这样规律的数.
3.【答案】C;
【解析】略
4.【答案】D;
【解析】解:①的倒数是,正确;
②,正确;
③,,,,的中位数是,原结论错误;
④,,,的众数是,原结论错误;
⑤,正确;
⑥,原结论错误.
所以他做对的题数是个.
故选:
①根据倒数的定义判断即可;②根据绝对值的定义判断即可;③根据中位数的定义判断即可;④根据众数的定义判断即可;⑤根据立方根的定义判断即可;⑥根据算术平方根的定义判断即可.
此题主要考查了众数,中位数,绝对值,立方根以及算术平方根,掌握相关定义是解答本题的关键.
5.【答案】B;
【解析】任何三角形都有三条高,它们相交于一点,
锐角三角形三条高的交点在形内,直角三角形三条高的交点就是直角顶点,钝角三角形只有一条高在形内,三条高的交点在形外,
而三角形的三条中线,三条角平分线都在三角形内部,
所以①③错误,②④正确。故答案为:B。
6.【答案】A;
【解析】
【分析】
本题主要考查了二次根式和绝对值的性质与化简.特别因为都是数轴上的实数,注意符号的变换.根据二次根式和绝对值的性质,化简解答. 【解答】解:由数轴可得,,根据二次根式和绝对值的性质,化简得,
,
,
.
故选A.
7.【答案】A;
【解析】解:,
最小的数是,
故选:
先根据实数的大小比较法则比较数的大小,再得出答案即可.
此题主要考查了实数的大小比较和算术平方根,能根据实数的大小比较法则比较数的大小是解此题的关键,注意:正数都大于,负数都小于,正数大于一切负数,两个负数比较大小,其绝对值大的反而小.
8.【答案】<;
【解析】解:,则,
,
故答案为:
根据,则,再判断负数即可.
此题主要考查实数大小比较,熟练根据正数的大小比较其相反数大小是解答该题的关键.
9.【答案】 ±2;
【解析】解:的算术平方根是,,的平方根是
故答案为:,
根据算术平方根、平方根的定义解答.
此题主要考查平方根和算术平方根,熟练掌握平方根和算术平方根的定义是解题关键.
10.【答案】,;
,
的平方根是;
【解析】
由介于和两个平方数之间,即可求得和的值;
由“逐步逼近”法知,可求得、的值,带入即可求得结果.
解:,
,即,
故答案为:,;
见答案.
11.【答案】-13;
【解析】解:原式
故答案为:
直接利用立方根的性质以及有理数的乘方运算法则分别化简,进而得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
12.【答案】17.6;
【解析】解:,是表中两个相邻的数,,
,
故答案为:
根据表中的数据进行解答即可.
此题主要考查估算无理数的大小,解答该题的关键是掌握算术平方根的定义.
13.【答案】;
【解析】
先把算式进行整理,再进行计算求解;
先计算平方、绝对值和算术平方根,再计算加减.
此题主要考查了实数混合运算的能力,关键是能准确确定计算顺序,并能进行正确地计算.
14.【答案】解:由题意得,x=±,y=±,
∵|y-x|=x-y,
∴x>y
∴x=,y=或x=,y=-.
∴x+y=+或x+y=-.;
【解析】
先依据绝对值和平方根的定义确定出、的值,然后依据绝对值的性质求得、可能的情况,最后进行计算即可.
这道题主要考查的是实数的性质、平方根的性质,分类讨论是解答该题的关键.
15.【答案】解:原式=,
=.;
【解析】【分析】
通过计算零指数幂、负指数幂、分母有理化、开平方的计算即可得出结论;
【点睛】本题主要考查了实数的计算,计算正确是解题的关键.
16.【答案】解:由题意得,,
解得,;
,
,
.;
【解析】、根据一个正数有两个平方根,这两个平方根互为相反数解答.
该题考查的是平方根的概念,掌握一个正数有两个平方根,这两个平方根互为相反数是解答该题的关键,
17.【答案】
解:根据,,
则,
答:这场雷雨大约能持续;
根据,其中,
答:这场雷雨区域的直径大约是;
【解析】
此题主要考查了算术平方根的应用,注意一个正数的算术平方根只有一个.
根据,其中是雷雨区域的直径,开平方的意义,可得答案;
根据,其中是雷雨区域的直径,开平方的意义,可得答案.
18.【答案】 ;
【解析】解:【问题】、分别是线段、的中点,
,,
;
【拓展】、分别是线段、的中点,
,,
故答案为:;
射线、分别平分、,
,,
故答案为:;
,,
,
又、分别平分、,
由结论可知,
,
,
,
与的差为
【问题】由点、分别是线段、的中点,可得,,因为,代入计算即可得出答案;
【拓展】解法同【问题】;
【应用】由射线、分别平分、,可得,,因为,代入即可得出答案;
根据平行线的性质可得,再根据中的结论可得出的度数,再根据三角形的外角定理,即可得出答案.
此题主要考查了平行线的性质,角平分线的性质及线段的中点,熟练掌握角平分线的性质和平行线的性质是解决本题的关键.
