2014年中考复习提能训练课件第四章 第1讲相交线和平行线
文档属性
| 名称 | 2014年中考复习提能训练课件第四章 第1讲相交线和平行线 |

|
|
| 格式 | zip | ||
| 文件大小 | 525.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:42:27 | ||
图片预览








文档简介
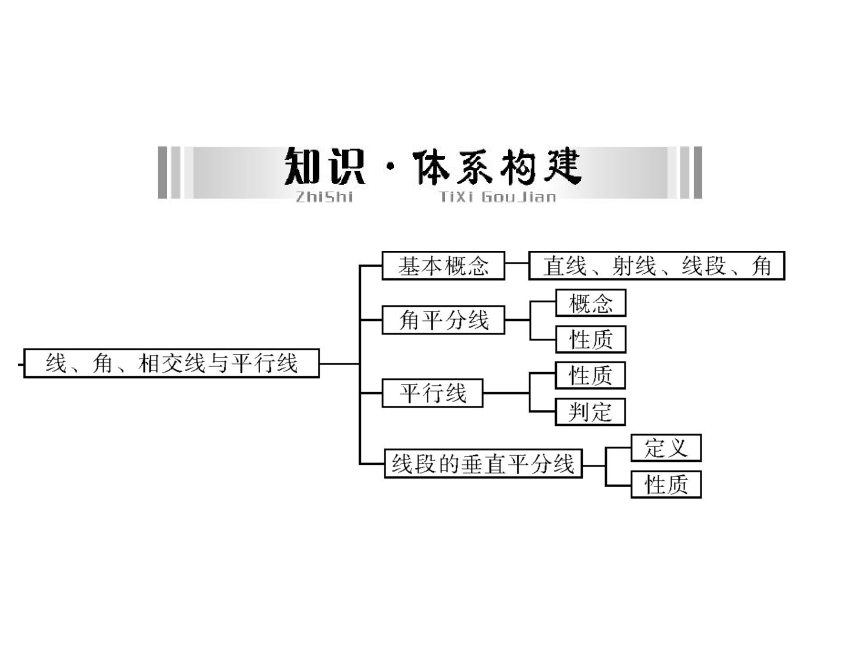
课件31张PPT。第四章 三角形与四边形1.会比较角的大小,能估计一个角的大小,会计算角度的和与差,认识度、分、秒,会进行简单换算.2.了解角平分线及其性质.3.了解补角、余角、对顶角,知道等角的余角相等、等角的补角相等、对顶角相等.第1讲相交线和平行线4.了解垂线、垂线段等概念,了解垂线段最短的性质,体会点到直线距离的意义.5.知道过一点有且仅有一条直线垂直于已知直线,会用三角尺或量角器过一点画一条直线的垂线.6.了解线段垂直平分线及其性质.7.知道两直线平行,同位角相等,进一步探索平行线的性质. 8.知道过直线外一点有且仅有一条直线平行于已知直线,
会用三角尺或直尺过已知直线外一点画这条直线的平行线.9.会度量两条平行线之间的距离.10.通过具体例子,了解定义、命题、逆命题、定理等相关概念,会识别两个互逆命题. 11.通过实例,理解反例的作用,体会反证法的含义,掌
握用综合法证明的格式,体会证明的过程要步步有据.考点1线与角一条线段1.直线公理:经过两点有且只有__________直线.
2.线段公理:两点之间,____________最短.
3.余角、补角与对项角.
(1)∠1+∠2=90°?∠1 与∠2 互为余角;同角(或等角)的余角________.相等补角相等 (2)∠1+∠2=180°?∠1 与∠2 互为________;同角(或等
角)的补角相等.
(3)对顶角________.考点2相交线1.垂线的性质.
性质 1:过一点有且只有__________直线与已知直线垂直.
性质 2 :直线外一点与直线上各点连接的所有线段中,__________最短.一条垂线段长度 2.点到直线的距离.
直线外一点到这条直线的垂线段的_______,叫做点到直线
的距离.考点3平行线的性质与判定1.在同一平面内,不重合的两条直线的位置关系只有两种:__________或 __________.相交平行一条 2.平行线公理:经过直线外一点,有且只有________直线
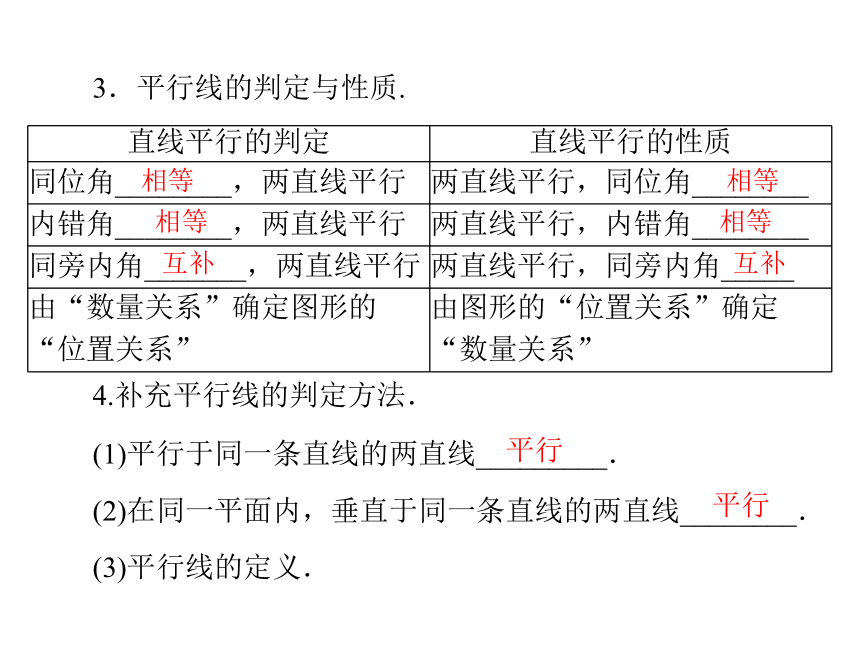
与这条直线平行.3.平行线的判定与性质.
4.补充平行线的判定方法.
(1)平行于同一条直线的两直线_________.
(2)在同一平面内,垂直于同一条直线的两直线________.(3)平行线的定义.平行平行相等相等相等相等互补互补考点4角平分线和线段的垂直平分线的性质与判定1.线段的垂直平分线.两端点两端点点 (1)性质:线段的垂直平分线上的点到这条线段的________
距离相等.
(2)其逆定理:到一条线段________距离相等的______,在
这条线段的垂直平分线上.
2.角平分线.
(1)性质:角平分线上的点到角的两边的距离_______.
(2)逆定理:角的内部到角的两边的距离________的点在角的角平分线上.相等相等考点5命题、定理、证明1.每个命题都是由______和______两部分组成.
2.真命题和假命题:正确的命题叫做____________,错误的命题叫做____________.题设结论3.用推理的方法判断为正确的命题叫做__________.【学有奇招】真命题假命题定理 1.以几何学具、实物为背景的角度计算题,注意运用学具
或实物中的平行关系、垂直关系,构造图形,然后计算相关角
度,关键是灵活处理与转化图形的位置关系和数量关系.
2.作辅助线.图中有角平分线,可向两边作垂线,线段垂
直平分线,常向两端把线连.1.如图 4-1-1,梯子的各条横档互相平行,若∠1=80°,则∠2 的度数是()BA.80°B.100°C.120°D.150°图 4-1-12.将一直角三角板与两边平行的纸条按图 4-1-2 所示放置,下列结论:D 图 4-1-2
①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5
=180°.其中正确的个数是()A.1 个B.2 个C.3 个D.4 个3.线段 AB=4 cm,在线段 AB 上截取 BC=1 cm,则 AC=__________cm.3④ 4.有如下命题:①三角形的三个内角和等于180°;②两直
线平行,同位角相等;③矩形的对角线相等;④相等的角是对
顶角.其中属于假命题的有__________.
5.如图4-1-3,在△ABC 中,∠A=90°,点 D在AC 边上,65°DE∥BC,若∠1=155°,则∠B 的度数为_____.图 4-1-3 与线(直线、射线、线段)、 角(互余、互补、垂直)有
关的计算
例题:(2013 年江苏南通)如图 4-1-4,直线 AB,CD 相交于
点 O,OE⊥AB,∠BOD=20°,则∠COE=__________.图4-1-4解析:由垂直关系构建互余计算.
∵OE⊥AB,∴∠EOA=90°.
∵∠AOC=∠BOD=20°,
∴∠COE=90°-20°=70°.
答案:70°【试题精选】
1.(2013 年湖南长沙)如图 4-1-5,BD 是∠ABC 的平分线,
P 是 BD 上的一点,PE⊥BA 于点 E,PE=4 cm,则点 P 到边40°BC 的距离为__________cm.
图 4-1-5
图 4-1-6 2.(2013 年云南曲靖)如图 4-1-6,直线 AB,CD 相交于点
O,若∠BOD=40°,OA 平分∠COE,则∠AOE=________.4 名师点评:在有关线、角、三角板等的背景图中,应着眼
于一些比较特殊的平角、角平分线、互余、互补的角、垂直等
概念,立足于基本性质,构建相关量之间的位置及数量大小关
系进行分析与解题. 与平行线性质、判定有关的计算与说理题
3.(2013 年江苏扬州)下列图形中,由 AB∥CD 能得到∠1=∠2 的是()B 4.(2013 年贵州六盘水)直尺与三角尺按如图 4-1-7 所示的
方式叠放在一起,在图中所标记的角中,与∠1 互余的角有几个(B )
A.2 个
C.4 个
B.3 个
D.5 个 解析:由于∠1 与∠2 互余,所以只要找出所有与∠2 相等
的角即可.
名师点评:考试中常设置某些数学元素(点、线、生活实物、
三角板学具等)的摆放与操作,酝酿与生成平行线、相交线等,
尤其是其中产生的角常与三角形中的内角、外角相联系.图 4-1-7识别命题的真假)A5.下列命题中,为真命题的是(
A.对顶角相等
B.同位角相等
C.若 a2=b2,则 a=b
D.若 a>b,则-2a>-2b 6.(2012 年四川广元)如图 4-1-8,在△AEC 和△DBF 中,
∠E=∠F,点 A,B,C,D 在同一条直线上.有如下三个关系
式:①AE∥DF;②AB=CD;③CE=BF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出
你认为正确的所有命题(用序号写出命题书写格式:如果 tan 60°=a+x
x,那么 x=a+x);(2)选择(1)中你写出的一个命题,说明它正确的理由.图 4-1-8解:(1)命题 1:如果①,②,那么③;
命题 2:如果①,③,那么②.
(2)命题 1 的证明如下:
∵AE∥DF, ∴∠A=∠D.
∵AB=CD,∴AB+BC=CD+BC,即 AC=DB.
在△AEC 和△DFB 中,∵∠E=∠F,∠A=∠D,AC=DB,∴△AEC≌△DFB(AAS).∴CE=BF.命题 2 的证明如下:∵AE∥DF, ∴∠A=∠D.
在△AEC 和△DFB 中,∵∠E=∠F,∠A=∠D,CE=BF,
∴△AEC≌△DFB(AAS).
∴AC=DB.则 AC—BC=DB—BC,即 AB=CD.名师点评:当所写命题不确定时,需分类讨论各种可能,逐步分层次探究及判断命题的真假.1.(2013 年广东珠海)如图 4-1-9,两平行直线 a,b 被直线l 所截,且∠1=60°,则∠2 的度数为()CA.30°B.45°C.60°D.120°图 4-1-92.(2013 年广东汕头)如图 4-4-10,AC∥DF,AB∥EF,点)D,E 分别在 AB,AC 上,若∠2=50°,则∠1 的大小是(
图 4-1-10A. 30°B. 40°C. 50°D. 60°C 解析:因为 AC∥DF,所以∠A=∠1.又因为 AB∥EF,所
以∠A=∠2,所以∠1=∠2,由∠2=50°,得∠1=50°.3 . (2013年广东佛山)命题“ 对顶角相等” 的条件是__________________.两个角是对顶角4.(2013 年广东广州)点 P 在线段 AB 的垂直平分线上,PA=7,则 PB=__________.75.(2013年广东梅州)若∠α=42°,则∠α的余角的度数是____________.48°6.(2012年广东广州)已知∠ABC=30°,BD 是∠ABC 的平分线,则∠ABD=__________.15° 7.(2011 年广东广州)已知三条不同的直线 a,b,c 在同一
平面内,下列四个命题:
①如果 a∥b,a⊥c,那么 b⊥c;②如果 b∥a,c∥a,那么
b∥c;
③如果 b⊥a,c⊥a,那么 b⊥c;④如果 b⊥a,c⊥a,那么b∥c.①②④其中真命题的是__________(填写所有真命题的序号).8.(2012 年广东佛山)比较两个角的大小,有以下两种方法(规则):①用量角器度量两个角的大小,用度数表示,则角度大的角大;②构造图形,如果一个角包含(或覆盖)另一个角,则这个角大.对于如图给定的∠ABC 与∠DEF,用以上两种方法分别比较它们的大小.注:构造图形时,作示意图(图 4-1-11)即可.图 4-1-11解:(1)用量角器分别量出两个角的度数,然后进行比较即可.
(2)如图 12.图 12故∠DEF 大.
会用三角尺或直尺过已知直线外一点画这条直线的平行线.9.会度量两条平行线之间的距离.10.通过具体例子,了解定义、命题、逆命题、定理等相关概念,会识别两个互逆命题. 11.通过实例,理解反例的作用,体会反证法的含义,掌
握用综合法证明的格式,体会证明的过程要步步有据.考点1线与角一条线段1.直线公理:经过两点有且只有__________直线.
2.线段公理:两点之间,____________最短.
3.余角、补角与对项角.
(1)∠1+∠2=90°?∠1 与∠2 互为余角;同角(或等角)的余角________.相等补角相等 (2)∠1+∠2=180°?∠1 与∠2 互为________;同角(或等
角)的补角相等.
(3)对顶角________.考点2相交线1.垂线的性质.
性质 1:过一点有且只有__________直线与已知直线垂直.
性质 2 :直线外一点与直线上各点连接的所有线段中,__________最短.一条垂线段长度 2.点到直线的距离.
直线外一点到这条直线的垂线段的_______,叫做点到直线
的距离.考点3平行线的性质与判定1.在同一平面内,不重合的两条直线的位置关系只有两种:__________或 __________.相交平行一条 2.平行线公理:经过直线外一点,有且只有________直线
与这条直线平行.3.平行线的判定与性质.
4.补充平行线的判定方法.
(1)平行于同一条直线的两直线_________.
(2)在同一平面内,垂直于同一条直线的两直线________.(3)平行线的定义.平行平行相等相等相等相等互补互补考点4角平分线和线段的垂直平分线的性质与判定1.线段的垂直平分线.两端点两端点点 (1)性质:线段的垂直平分线上的点到这条线段的________
距离相等.
(2)其逆定理:到一条线段________距离相等的______,在
这条线段的垂直平分线上.
2.角平分线.
(1)性质:角平分线上的点到角的两边的距离_______.
(2)逆定理:角的内部到角的两边的距离________的点在角的角平分线上.相等相等考点5命题、定理、证明1.每个命题都是由______和______两部分组成.
2.真命题和假命题:正确的命题叫做____________,错误的命题叫做____________.题设结论3.用推理的方法判断为正确的命题叫做__________.【学有奇招】真命题假命题定理 1.以几何学具、实物为背景的角度计算题,注意运用学具
或实物中的平行关系、垂直关系,构造图形,然后计算相关角
度,关键是灵活处理与转化图形的位置关系和数量关系.
2.作辅助线.图中有角平分线,可向两边作垂线,线段垂
直平分线,常向两端把线连.1.如图 4-1-1,梯子的各条横档互相平行,若∠1=80°,则∠2 的度数是()BA.80°B.100°C.120°D.150°图 4-1-12.将一直角三角板与两边平行的纸条按图 4-1-2 所示放置,下列结论:D 图 4-1-2
①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5
=180°.其中正确的个数是()A.1 个B.2 个C.3 个D.4 个3.线段 AB=4 cm,在线段 AB 上截取 BC=1 cm,则 AC=__________cm.3④ 4.有如下命题:①三角形的三个内角和等于180°;②两直
线平行,同位角相等;③矩形的对角线相等;④相等的角是对
顶角.其中属于假命题的有__________.
5.如图4-1-3,在△ABC 中,∠A=90°,点 D在AC 边上,65°DE∥BC,若∠1=155°,则∠B 的度数为_____.图 4-1-3 与线(直线、射线、线段)、 角(互余、互补、垂直)有
关的计算
例题:(2013 年江苏南通)如图 4-1-4,直线 AB,CD 相交于
点 O,OE⊥AB,∠BOD=20°,则∠COE=__________.图4-1-4解析:由垂直关系构建互余计算.
∵OE⊥AB,∴∠EOA=90°.
∵∠AOC=∠BOD=20°,
∴∠COE=90°-20°=70°.
答案:70°【试题精选】
1.(2013 年湖南长沙)如图 4-1-5,BD 是∠ABC 的平分线,
P 是 BD 上的一点,PE⊥BA 于点 E,PE=4 cm,则点 P 到边40°BC 的距离为__________cm.
图 4-1-5
图 4-1-6 2.(2013 年云南曲靖)如图 4-1-6,直线 AB,CD 相交于点
O,若∠BOD=40°,OA 平分∠COE,则∠AOE=________.4 名师点评:在有关线、角、三角板等的背景图中,应着眼
于一些比较特殊的平角、角平分线、互余、互补的角、垂直等
概念,立足于基本性质,构建相关量之间的位置及数量大小关
系进行分析与解题. 与平行线性质、判定有关的计算与说理题
3.(2013 年江苏扬州)下列图形中,由 AB∥CD 能得到∠1=∠2 的是()B 4.(2013 年贵州六盘水)直尺与三角尺按如图 4-1-7 所示的
方式叠放在一起,在图中所标记的角中,与∠1 互余的角有几个(B )
A.2 个
C.4 个
B.3 个
D.5 个 解析:由于∠1 与∠2 互余,所以只要找出所有与∠2 相等
的角即可.
名师点评:考试中常设置某些数学元素(点、线、生活实物、
三角板学具等)的摆放与操作,酝酿与生成平行线、相交线等,
尤其是其中产生的角常与三角形中的内角、外角相联系.图 4-1-7识别命题的真假)A5.下列命题中,为真命题的是(
A.对顶角相等
B.同位角相等
C.若 a2=b2,则 a=b
D.若 a>b,则-2a>-2b 6.(2012 年四川广元)如图 4-1-8,在△AEC 和△DBF 中,
∠E=∠F,点 A,B,C,D 在同一条直线上.有如下三个关系
式:①AE∥DF;②AB=CD;③CE=BF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出
你认为正确的所有命题(用序号写出命题书写格式:如果 tan 60°=a+x
x,那么 x=a+x);(2)选择(1)中你写出的一个命题,说明它正确的理由.图 4-1-8解:(1)命题 1:如果①,②,那么③;
命题 2:如果①,③,那么②.
(2)命题 1 的证明如下:
∵AE∥DF, ∴∠A=∠D.
∵AB=CD,∴AB+BC=CD+BC,即 AC=DB.
在△AEC 和△DFB 中,∵∠E=∠F,∠A=∠D,AC=DB,∴△AEC≌△DFB(AAS).∴CE=BF.命题 2 的证明如下:∵AE∥DF, ∴∠A=∠D.
在△AEC 和△DFB 中,∵∠E=∠F,∠A=∠D,CE=BF,
∴△AEC≌△DFB(AAS).
∴AC=DB.则 AC—BC=DB—BC,即 AB=CD.名师点评:当所写命题不确定时,需分类讨论各种可能,逐步分层次探究及判断命题的真假.1.(2013 年广东珠海)如图 4-1-9,两平行直线 a,b 被直线l 所截,且∠1=60°,则∠2 的度数为()CA.30°B.45°C.60°D.120°图 4-1-92.(2013 年广东汕头)如图 4-4-10,AC∥DF,AB∥EF,点)D,E 分别在 AB,AC 上,若∠2=50°,则∠1 的大小是(
图 4-1-10A. 30°B. 40°C. 50°D. 60°C 解析:因为 AC∥DF,所以∠A=∠1.又因为 AB∥EF,所
以∠A=∠2,所以∠1=∠2,由∠2=50°,得∠1=50°.3 . (2013年广东佛山)命题“ 对顶角相等” 的条件是__________________.两个角是对顶角4.(2013 年广东广州)点 P 在线段 AB 的垂直平分线上,PA=7,则 PB=__________.75.(2013年广东梅州)若∠α=42°,则∠α的余角的度数是____________.48°6.(2012年广东广州)已知∠ABC=30°,BD 是∠ABC 的平分线,则∠ABD=__________.15° 7.(2011 年广东广州)已知三条不同的直线 a,b,c 在同一
平面内,下列四个命题:
①如果 a∥b,a⊥c,那么 b⊥c;②如果 b∥a,c∥a,那么
b∥c;
③如果 b⊥a,c⊥a,那么 b⊥c;④如果 b⊥a,c⊥a,那么b∥c.①②④其中真命题的是__________(填写所有真命题的序号).8.(2012 年广东佛山)比较两个角的大小,有以下两种方法(规则):①用量角器度量两个角的大小,用度数表示,则角度大的角大;②构造图形,如果一个角包含(或覆盖)另一个角,则这个角大.对于如图给定的∠ABC 与∠DEF,用以上两种方法分别比较它们的大小.注:构造图形时,作示意图(图 4-1-11)即可.图 4-1-11解:(1)用量角器分别量出两个角的度数,然后进行比较即可.
(2)如图 12.图 12故∠DEF 大.
同课章节目录
