2014年中考复习提能训练课件第五章 第3讲与圆有关的计算
文档属性
| 名称 | 2014年中考复习提能训练课件第五章 第3讲与圆有关的计算 |

|
|
| 格式 | zip | ||
| 文件大小 | 348.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:41:11 | ||
图片预览








文档简介
课件22张PPT。第3讲与圆有关的计算1.会计算弧长及扇形的面积.
2.会计算圆锥的侧面积和全面积.考点 1扇形、圆柱与圆锥的有关计算1.设扇形所在圆的半径为 r,圆心角为 n°,则(1)扇形的弧长:l=________.(2)扇形的面积:S=_______=__________.2.设圆柱的底面半径为 r,高为 h,底面周长为 C,则矩形2πrh(1)圆柱的侧面展开图是_________.
(2)圆柱的侧面积:S=Ch=________.(3)圆柱的全面积:S全=_____________.2πrh+2πr23.设圆锥的底面半径为 r,底面周长为 C,则
(1) 母线长为l的侧面展开图( 扇形) 的圆心角为α ,则α =________.πrl(2)圆锥的侧面积:S侧=________=________.(3)圆锥的全面积:S全=__________.πr2+πrl考点2正多边形与圆相等相等1.正多边形:各边________,各角________的多边形叫做正多边形.中心半径中心角边心距 2.圆与正多边形的有关概念:一个正多边形的外接圆的圆
心叫做这个正多边形的______,外接圆的半径叫做正多边形的
_____;正多边形每一边所对的圆心角叫做正多边形的_______,
中心到正多边形的一边的距离叫做正多边形的________.
3.正多边形的内角和=____________;正多边形的每个内
角=______________;正多边形的周长=边长×边数;正多边
形的面积=_______________ .(n-2)×180°【学有奇招】1
2了方便记忆,可把扇形理解为一个曲边三角形,把 l 看作底,r 看
作底边上的高. 2.不规则图形的面积计算:①求不规则图形的面积关键是转
化:将不规则图形转化为规则图形;②求阴影部分的面积方法常
用的有:公式法、割补法、拼凑法、等积变形法、构造方程法等.
3.有关正 n 边形的计算,边心距、半径是关键,内切、外接
圆半径,边心距、半径分别换,分成直角三角形,依此计算很简
单.1.扇形面积公式S扇形=—lr与三角形面积公式十分类似.为1.在半径为 12 的⊙O 中,60°圆心角所对的弧长是()A.6πB.4πC.2πD.πB2.用一个圆心角为 120°,半径为 2 的扇形做一个圆锥的侧面,则这个圆锥的底面圆半径为()DA.4
3B.3
4C.3
2D.2
31
2心角是__________.90°3.圆锥底面半径为—,母线长为2,它的侧面展开图的圆
4.正多边形的一个内角为120°,则该多边形的边数为___.
5.如图 5-3-1,⊙A、⊙B、⊙C 两两外切,它们的半径都
是a ,顺次连接三个圆心得到△ABC,则图中阴影部分的面积之和是__________.图 5-3-16 扇形的弧长和面积计算
1.(2013 年四川资阳)钟面上的分针的长为 1,从 9 点到 9点 30 分,分针在钟面上扫过的面积是()A 1
A. π
2 1
B. π
4 1
C. π
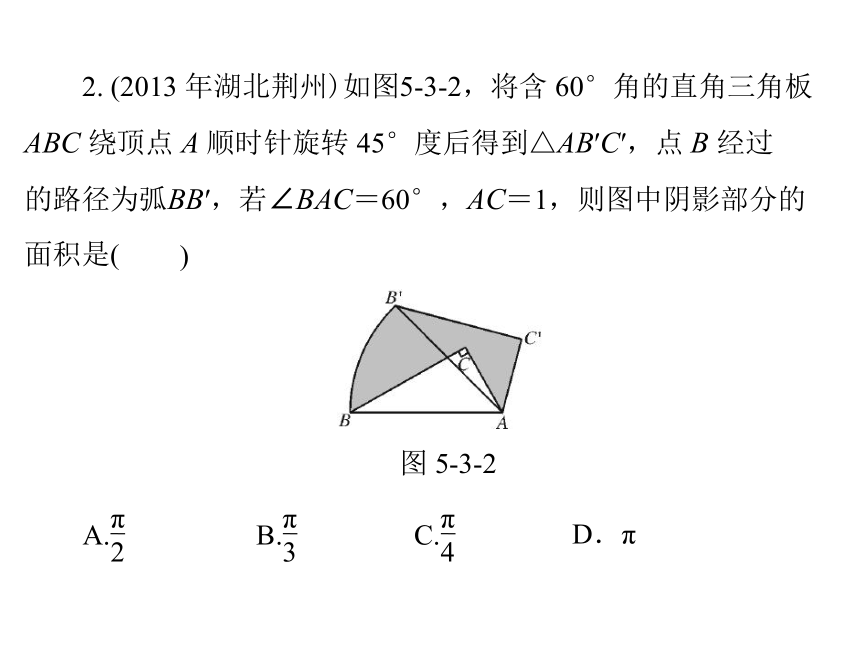
8D. π 2. (2013 年湖北荆州)如图5-3-2,将含 60°角的直角三角板
ABC 绕顶点 A 顺时针旋转 45°度后得到△AB′C′,点 B 经过
的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是()图 5-3-2A.π
2B.π
3C.π
4D.π答案:A 圆柱体和圆锥的侧面积和全面积
3.(2013 年湖北黄冈)已知一个圆柱的侧面展开图为如图)图 5-3-35-3-3所示的矩形,则其底面圆的面积为(
A.π B.4π
C.π或 4π D.2π或 4π 解析:当底面圆周长为 4π时,2πr=4π,r=2,S=πr2
=4π;当底面圆周长为 2π时,2πr=2π,r=1,S=πr2=
π.则底面圆的面积为π或 4π.
答案:C片上剪去—圆周的一个扇形,将留下的扇形围成一个圆锥(接缝4.(2013 年四川泸州)如图 5-3-4,从半径为 9 cm 的圆形纸1
3处不重叠),那么这个圆锥的高为____________cm.图 5-3-4
答案:3
名师点评:有关立体图形问题,常转化为平面图形来解决,
圆锥的侧面展开图是扇形,圆锥的高不等于圆锥的母线长,要
注意圆锥的母线长在展开成平面图形后成为扇形的半径. 正多边形和圆
5.(2013 年山东滨州)若正方形的边长为 6,则其外接圆半径与内切圆半径的大小分别为()B6.(2013 年四川绵阳)如图 5-3-5,要拧开一个边长为 a=6 cm 的正六边形螺帽,扳手张开的开口 b 至少为()图 5-3-5答案:C 名师点评:解决正多边形的相关计算问题的关键在于添加
辅助线(边心距和半径),将其转化为直角三角形运用勾股定理
来解决.1.(2011 年广东肇庆)已知正六边形的边心距为 ,则它的)B周长是(
A.6B.12C.6D.1215π 2.(2013 年广东珠海)若圆锥的母线长为 5 cm,底面圆的半
径为 3 cm,则它的侧面展开图的面积为______ cm2(结果保留π). 3.(2013 年广东茂名)图 5-3-6 是李大妈跳舞用的扇子,这
个扇形 AOB 的圆心角∠O=120°,半径 OA=3,则弧 AB 的长2π度为__________(结果保留π).
图 5-3-6度数之和为 135°,所以图中阴影部分面积的和为 4.(2013 年广东)如图 5-3-7,三个小正方形的边长都为 1,
则图中阴影部分面积的和是________(结果保留π).
图 5-3-7
解析:图中三块阴影部分都是扇形,且半径相等,由平行线
内错角相等和正方形的对角线的性质可知,三个扇形的圆心角的 5.(2013 年广东佛山)如图 5-3-8,圆锥的侧面展开图是一
个半圆,求母线 AB 与高 AO 的夹角.
(参考公式:圆锥的侧面积 S=πrl,其中 r 为底面半径,l 为母线长)图 5-3-8解:因为 2πr=πl.所以 l=2r,
r 1
l 2
所以母线 AB 与高 AO 的夹角为 30°.所以sin∠BAO=—=—,所以∠BAO=30°, 6.(2013 年广东梅州)如图 5-3-9,在矩形 ABCD 中,AB=
2DA,以点 A 为圆心,AB 为半径的圆弧交 DC 于点 E,交 AD
的延长线于点 F,设 DA=2.(1)求线段 EC 的长;(2)求图中阴影部分的面积.图 5-3-9
2.会计算圆锥的侧面积和全面积.考点 1扇形、圆柱与圆锥的有关计算1.设扇形所在圆的半径为 r,圆心角为 n°,则(1)扇形的弧长:l=________.(2)扇形的面积:S=_______=__________.2.设圆柱的底面半径为 r,高为 h,底面周长为 C,则矩形2πrh(1)圆柱的侧面展开图是_________.
(2)圆柱的侧面积:S=Ch=________.(3)圆柱的全面积:S全=_____________.2πrh+2πr23.设圆锥的底面半径为 r,底面周长为 C,则
(1) 母线长为l的侧面展开图( 扇形) 的圆心角为α ,则α =________.πrl(2)圆锥的侧面积:S侧=________=________.(3)圆锥的全面积:S全=__________.πr2+πrl考点2正多边形与圆相等相等1.正多边形:各边________,各角________的多边形叫做正多边形.中心半径中心角边心距 2.圆与正多边形的有关概念:一个正多边形的外接圆的圆
心叫做这个正多边形的______,外接圆的半径叫做正多边形的
_____;正多边形每一边所对的圆心角叫做正多边形的_______,
中心到正多边形的一边的距离叫做正多边形的________.
3.正多边形的内角和=____________;正多边形的每个内
角=______________;正多边形的周长=边长×边数;正多边
形的面积=_______________ .(n-2)×180°【学有奇招】1
2了方便记忆,可把扇形理解为一个曲边三角形,把 l 看作底,r 看
作底边上的高. 2.不规则图形的面积计算:①求不规则图形的面积关键是转
化:将不规则图形转化为规则图形;②求阴影部分的面积方法常
用的有:公式法、割补法、拼凑法、等积变形法、构造方程法等.
3.有关正 n 边形的计算,边心距、半径是关键,内切、外接
圆半径,边心距、半径分别换,分成直角三角形,依此计算很简
单.1.扇形面积公式S扇形=—lr与三角形面积公式十分类似.为1.在半径为 12 的⊙O 中,60°圆心角所对的弧长是()A.6πB.4πC.2πD.πB2.用一个圆心角为 120°,半径为 2 的扇形做一个圆锥的侧面,则这个圆锥的底面圆半径为()DA.4
3B.3
4C.3
2D.2
31
2心角是__________.90°3.圆锥底面半径为—,母线长为2,它的侧面展开图的圆
4.正多边形的一个内角为120°,则该多边形的边数为___.
5.如图 5-3-1,⊙A、⊙B、⊙C 两两外切,它们的半径都
是a ,顺次连接三个圆心得到△ABC,则图中阴影部分的面积之和是__________.图 5-3-16 扇形的弧长和面积计算
1.(2013 年四川资阳)钟面上的分针的长为 1,从 9 点到 9点 30 分,分针在钟面上扫过的面积是()A 1
A. π
2 1
B. π
4 1
C. π
8D. π 2. (2013 年湖北荆州)如图5-3-2,将含 60°角的直角三角板
ABC 绕顶点 A 顺时针旋转 45°度后得到△AB′C′,点 B 经过
的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是()图 5-3-2A.π
2B.π
3C.π
4D.π答案:A 圆柱体和圆锥的侧面积和全面积
3.(2013 年湖北黄冈)已知一个圆柱的侧面展开图为如图)图 5-3-35-3-3所示的矩形,则其底面圆的面积为(
A.π B.4π
C.π或 4π D.2π或 4π 解析:当底面圆周长为 4π时,2πr=4π,r=2,S=πr2
=4π;当底面圆周长为 2π时,2πr=2π,r=1,S=πr2=
π.则底面圆的面积为π或 4π.
答案:C片上剪去—圆周的一个扇形,将留下的扇形围成一个圆锥(接缝4.(2013 年四川泸州)如图 5-3-4,从半径为 9 cm 的圆形纸1
3处不重叠),那么这个圆锥的高为____________cm.图 5-3-4
答案:3
名师点评:有关立体图形问题,常转化为平面图形来解决,
圆锥的侧面展开图是扇形,圆锥的高不等于圆锥的母线长,要
注意圆锥的母线长在展开成平面图形后成为扇形的半径. 正多边形和圆
5.(2013 年山东滨州)若正方形的边长为 6,则其外接圆半径与内切圆半径的大小分别为()B6.(2013 年四川绵阳)如图 5-3-5,要拧开一个边长为 a=6 cm 的正六边形螺帽,扳手张开的开口 b 至少为()图 5-3-5答案:C 名师点评:解决正多边形的相关计算问题的关键在于添加
辅助线(边心距和半径),将其转化为直角三角形运用勾股定理
来解决.1.(2011 年广东肇庆)已知正六边形的边心距为 ,则它的)B周长是(
A.6B.12C.6D.1215π 2.(2013 年广东珠海)若圆锥的母线长为 5 cm,底面圆的半
径为 3 cm,则它的侧面展开图的面积为______ cm2(结果保留π). 3.(2013 年广东茂名)图 5-3-6 是李大妈跳舞用的扇子,这
个扇形 AOB 的圆心角∠O=120°,半径 OA=3,则弧 AB 的长2π度为__________(结果保留π).
图 5-3-6度数之和为 135°,所以图中阴影部分面积的和为 4.(2013 年广东)如图 5-3-7,三个小正方形的边长都为 1,
则图中阴影部分面积的和是________(结果保留π).
图 5-3-7
解析:图中三块阴影部分都是扇形,且半径相等,由平行线
内错角相等和正方形的对角线的性质可知,三个扇形的圆心角的 5.(2013 年广东佛山)如图 5-3-8,圆锥的侧面展开图是一
个半圆,求母线 AB 与高 AO 的夹角.
(参考公式:圆锥的侧面积 S=πrl,其中 r 为底面半径,l 为母线长)图 5-3-8解:因为 2πr=πl.所以 l=2r,
r 1
l 2
所以母线 AB 与高 AO 的夹角为 30°.所以sin∠BAO=—=—,所以∠BAO=30°, 6.(2013 年广东梅州)如图 5-3-9,在矩形 ABCD 中,AB=
2DA,以点 A 为圆心,AB 为半径的圆弧交 DC 于点 E,交 AD
的延长线于点 F,设 DA=2.(1)求线段 EC 的长;(2)求图中阴影部分的面积.图 5-3-9
同课章节目录
