2014年中考复习训练课件第三章 第1讲函数与平面直角坐标系
文档属性
| 名称 | 2014年中考复习训练课件第三章 第1讲函数与平面直角坐标系 |
|
|
| 格式 | zip | ||
| 文件大小 | 627.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:44:18 | ||
图片预览









文档简介
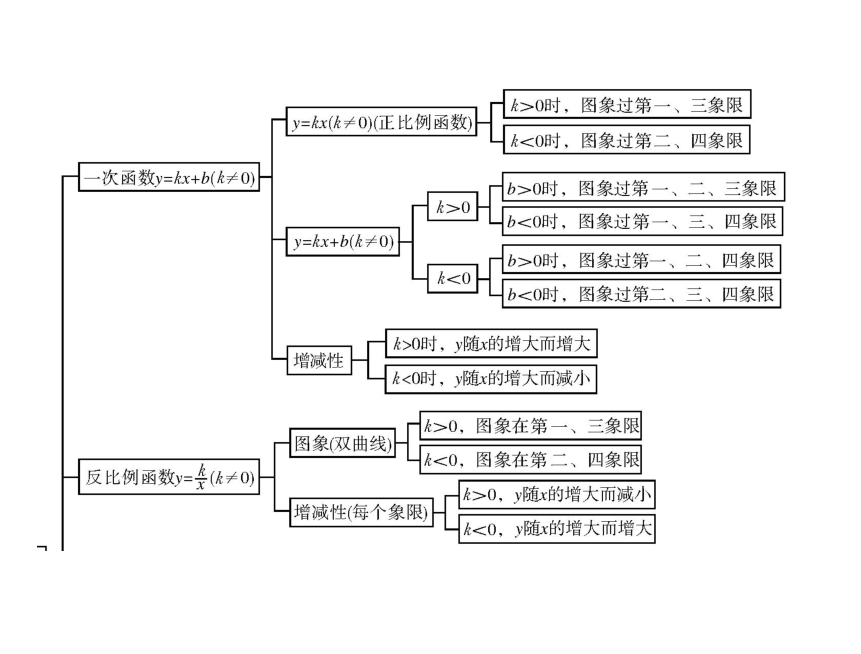
课件31张PPT。第三章 函数第1讲函数与平面直角坐标系 1.通过简单实例,了解常量、变量的意义.
2.能结合实例,了解函数的概念和三种表示方法,能举出
函数的实例.
3.能结合图象对简单实际问题中的函数关系进行分析.4.能确定简单的整式、分式和简单实际问题中的函数的自变量取值范围,并会求出函数值.5.能用适当的函数表示法刻画某些实际问题中变量之间的关系.6.结合对函数关系的分析,尝试对变量的变化规律进行初步预测.考点 1平面直角坐标系1.平面直角坐标系.公共原点互相垂直(1)定义:在平面内有____________且__________的两条数轴构成平面直角坐标系.一一对应 (2)坐标平面内任意一点 M 与有序实数对(x,y)的关系是
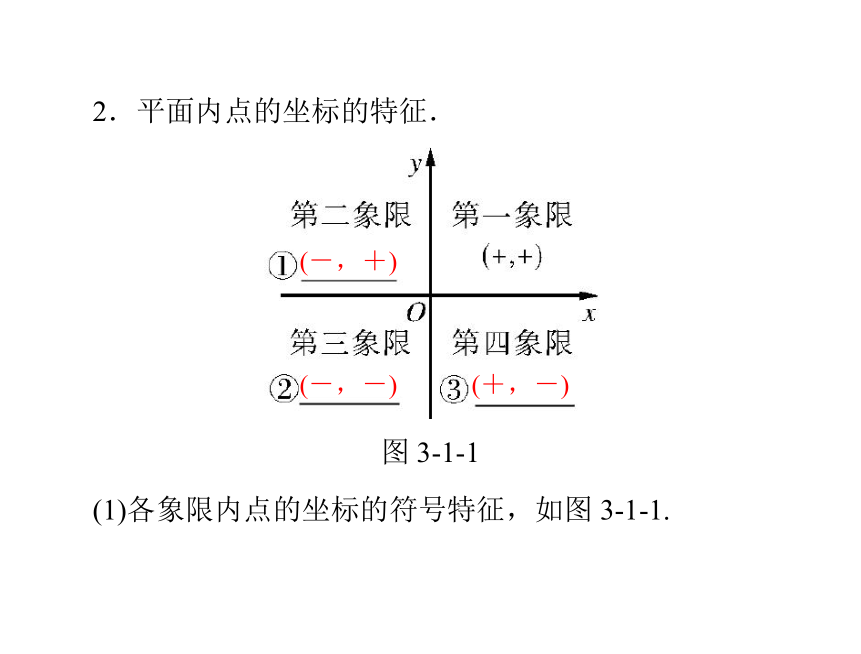
____________.2.平面内点的坐标的特征.
图 3-1-1
(1)各象限内点的坐标的符号特征,如图 3-1-1.(-,+)(-,-)(+,-)(2)坐标轴上的点 P(x,y)的特征:0000①在横轴上?y=_________;②在纵轴上?x=_________;相等互为相反数③既在横轴上,又在纵轴上?x=______,y=______.
(3)两条坐标轴夹角平分线上点 P(x,y)的特征:
①在第一、三象限夹角平分线上?x 与 y_______;
②在第二、四象限夹角平分线上?x 与 y_____________.
(4)和坐标轴平行的直线上点的坐标的特征:
①平行于 x 轴?________相同;②平行于 y 轴?_________相同.纵坐标横坐标3.对称点的坐标.已知点 P(a,b),(-a,b)(-a,-b)(1)其关于 x 轴对称的点 P1 的坐标为__________.
(2)其关于 y 轴对称的点 P2 的坐标为__________.
(3)其关于原点对称的点 P3 的坐标为__________.
4.点与点、点与线之间的距离.(1)点 M(a,b)到 x 轴的距离为________.
(2)点 M(a,b)到 y 轴的距离为________.|b|
|a|(3)点 M1(x1,0),M2(x2,0)之间的距离为________.|x1-x2|(4)点 M1(0,y1),M2(0,y2)之间的距离为_______.(a,-b)|y1-y2|考点2确定自变量的取值范围1.常量、变量.常量变量 在一个变化过程中,始终保持不变的量叫做_________,可
以取不同数值的量叫做_________.2.函数.唯一确定 (1)概念:在一个变化过程中,有两个变量 x 和 y,对于 x
的每一个值,y 都有__________的值与其对应,那么就称 x 是自
变量,y 是 x 的函数.(2)确定函数自变量的取值范围:有意义 ①使函数关系式________的自变量的取值的全体;
②一般原则为:整式为全体实数;分式的分母不为零;开
偶次方的被开方数为非负数;使实际问题有意义.
(3)函数的表示法:_______________、_______、_______.考点3函数及其图象画函数图象的步骤:列表、________、连线.解析法(公式法)列表法图象法描点【学有奇招】 平面直角坐标系中点的坐标的特征的记忆与理解可以通过
画图来解决,实践可以加深对知识的理解和记忆.平移的特点:
左右移,纵不变,横减加;上下移,横不变,纵加减.对称点
的坐标规律:关于 x 轴对称的点,横坐标相同,纵坐标互为相
反数;关于 y 轴对称的点,纵坐标相同,横坐标互为相反数.1.点 M(-2,1)关于 y 轴对称的点的坐标是()BA.(-2,-1)
C.(2,-1)B.(2,1)
D.(1,-2)2.如果点 P(a,2)在第二象限,那么点 Q(-3,a)在()CA.第一象限
C.第三象限B.第二象限
D.第四象限3.图 3-1-2 是象棋盘的一部分,若帅位于点(1,-2)上,)C相位于点(3,-2)上,则炮位于点(
A.(-1,1) B.(-1,2)C.(-2,1)D.(-2,2)图 3-1-24.函数 y= 2
x+1的自变量的取值范围是________.x≠-1 5.如图 3-1-3,将三角形向右平移 2 个单位长度,再向上
平移 3 个单位长度,则平移后三角形的三个坐标分别是____________________. (1,7),(3,4),(-2,2)
图 3-1-3平面直角坐标系 例题:(2013 年四川雅安)在平面直角坐标系中,已知点
A(- ,0),B( ,0),点 C 在坐标轴上,且 AC+BC=6,
写出满足条件的所有点 C 的坐标______________________.
思路分析:需要分类讨论:①当点 C 位于 x 轴上时,根据
线段间的和差关系即可求得点 C 的坐标;②当点 C 位于y 轴上
时,根据勾股定理求点 C 的坐标.答案:(0,2),(0,-2),(-3,0),(3,0)图3-1-4【试题精选】
1.(2013 年辽宁大连)在平面直角坐标系中,点(2,-4)在第________象限.四 2.(2012 年山东青岛)如图 3-1-5,将四边形 ABCD 先向左
平移 3 个单位长度,再向上平移 2 个单位长度,那么点 A 的对应点 A′的坐标是()B图 3-1-5A.(6,1)
B.(0,1)
C.(0,-3)
D.(6,-3) 名师点评:在平面直角坐标系中,图形的平移与图形上某
点的平移相同.平移中点的变化规律是:横坐标右移加,左移
减;纵坐标上移加,下移减.函数自变量的取值范围 2x
x-5中,自变量 x 的取值范 3.(2013 年辽宁营口)函数 y=
围是________. 4.(2013 年辽宁铁岭)函数 y=有意义,则自变量 x的取值范围是_____________.x≥1 且 x≠2 名师点评:确定函数自变量取值范围主要看三个方面:①
分母不为0;②偶次根式的被开方数是非负数;③出现0 指数,
底数不等于 0.x≠5 函数的图象及应用
例题:(2013 年湖北鄂州)如图 3-1-6,一个大烧杯中装有一
个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)
后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后
水溢出到大烧杯中,浮子始终保持在容器的正中
间.用 x 表示注水时间,用 y 表示浮子的高度,则用来表示 y 与 x 之间关系的选项是()图 3-1-6 解析:①小烧杯未被注满,这段时间,浮子的高度快速增
加;②小烧杯被注满,大烧杯内水面的高度还未达到小烧杯的
高度,此时浮子高度不变;③大烧杯内的水面高于小烧杯,此
时浮子高度缓慢增加.结合图象可得 B 选项的图象符合.答案:B【试题精选】B 5.(2013 年辽宁营口)如图 3-1-7(1),在矩形 ABCD 中,动
点 E 从点 B 出发,沿 BADC 方向运动至点 C 处停止.设点 E
运动的路程为 x,△BCE 的面积为 y,如果 y 关于 x 的函数图象如图 3-1-7(2)所示,那么当 x=7 时,点 E 应运动到()(1)(2)A.点 C 处B.点 D 处C.点 B 处D.点 A 处图3-1-7 6.(2013 年湖南衡阳)如图3-1-8,半径为1 的圆和边长为 3
的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正
方形,设穿过时间为 t,正方形除去圆部分的面积为 s(阴影部分),则 s 与 t 的大致图象为()A图3-1-8 名师点评:解决此类题目,一要明确横、纵轴所表示的实
际意义;二要结合实际分析:当横轴上的变量逐渐增大时,纵
轴上的变量如何变化?如果变大,图象表现为上升;如果变小,
图象表现为下降;如果不变,图象表现为与横轴平行.1.(2013 年广东湛江)在平面直角坐标系中,点 A(2,-3)在第()象限.()DA.一
C.三B.二
D.四2.(2013 年广东珠海)点(3,2)关于 x 轴的对称点为()AA.(3,-2)
C.(-3,-2)B.(-3,2)
D.(2,-3)3.(2011 年广东广州)当实数 x 的取值使得 有意义时,函数 y=4x+1 中 y 的取值范围是()BA.y≥-7
C.y>9 B.y≥9
D.y≤9 4.(2013 年广东佛山)某人匀速跑步到公园,在公园某处停
留了一段时间,再沿原路匀速步行回家,此人离家的距离 y 与时间 x 的关系的大致图象是()B 5. (2012 年广东珠海)如图 3-1-9,矩形 OABC 的顶点 A、C
分别在 x 轴、y 轴的正半轴上,点 B 的坐标为(3,2),OB 与 AC
交于点 P,点 D,E,F,G 分别是线段 OP,AP,BP,CP 的中5点,则四边形 DEFG 的周长为________.
图 3-1-9 6.(2013 年广东广州)如图 3-1-10,在平面直角坐标系中,
点 O 为坐标原点,点 P 在第一象限,⊙P 与 x 轴交于 O,A 两
点,点 A 的坐标为(6,0),⊙P 的半径为 ,则点 P 的坐标为__________.图 3-1-10(3,2) 7.(2013 年广东梅州)如图 3-1-11,在平面直角坐标系中,
点 A(-2,2),B(-3,-2).
图 3-1-11
(1) 若 点 C与点 A 关于原点 O 对 称 , 则 点 C 的 坐 标 为____________;(2,-2)(2)将点 A 向右平移 5 个单位长度得到点 D,则点 D 的坐标为____________;(3,2) (3)由点 A,B,C,D 组成的四边形 ABCD 内(不包括边界)
任取一个横、纵坐标均为整数的点,求所取的点横、纵坐标之
和恰好为零的概率.
答案:由(1)、(2)可知:A(-2,2),B(-3,-2),C(2,-2),
D(3,2).∵在平行四边形 ABCD 内横、纵坐标均为整数的点有
15 个,其中横、纵坐标和为零的点有3个,即(-1,1),(0,0),(1,
2.能结合实例,了解函数的概念和三种表示方法,能举出
函数的实例.
3.能结合图象对简单实际问题中的函数关系进行分析.4.能确定简单的整式、分式和简单实际问题中的函数的自变量取值范围,并会求出函数值.5.能用适当的函数表示法刻画某些实际问题中变量之间的关系.6.结合对函数关系的分析,尝试对变量的变化规律进行初步预测.考点 1平面直角坐标系1.平面直角坐标系.公共原点互相垂直(1)定义:在平面内有____________且__________的两条数轴构成平面直角坐标系.一一对应 (2)坐标平面内任意一点 M 与有序实数对(x,y)的关系是
____________.2.平面内点的坐标的特征.
图 3-1-1
(1)各象限内点的坐标的符号特征,如图 3-1-1.(-,+)(-,-)(+,-)(2)坐标轴上的点 P(x,y)的特征:0000①在横轴上?y=_________;②在纵轴上?x=_________;相等互为相反数③既在横轴上,又在纵轴上?x=______,y=______.
(3)两条坐标轴夹角平分线上点 P(x,y)的特征:
①在第一、三象限夹角平分线上?x 与 y_______;
②在第二、四象限夹角平分线上?x 与 y_____________.
(4)和坐标轴平行的直线上点的坐标的特征:
①平行于 x 轴?________相同;②平行于 y 轴?_________相同.纵坐标横坐标3.对称点的坐标.已知点 P(a,b),(-a,b)(-a,-b)(1)其关于 x 轴对称的点 P1 的坐标为__________.
(2)其关于 y 轴对称的点 P2 的坐标为__________.
(3)其关于原点对称的点 P3 的坐标为__________.
4.点与点、点与线之间的距离.(1)点 M(a,b)到 x 轴的距离为________.
(2)点 M(a,b)到 y 轴的距离为________.|b|
|a|(3)点 M1(x1,0),M2(x2,0)之间的距离为________.|x1-x2|(4)点 M1(0,y1),M2(0,y2)之间的距离为_______.(a,-b)|y1-y2|考点2确定自变量的取值范围1.常量、变量.常量变量 在一个变化过程中,始终保持不变的量叫做_________,可
以取不同数值的量叫做_________.2.函数.唯一确定 (1)概念:在一个变化过程中,有两个变量 x 和 y,对于 x
的每一个值,y 都有__________的值与其对应,那么就称 x 是自
变量,y 是 x 的函数.(2)确定函数自变量的取值范围:有意义 ①使函数关系式________的自变量的取值的全体;
②一般原则为:整式为全体实数;分式的分母不为零;开
偶次方的被开方数为非负数;使实际问题有意义.
(3)函数的表示法:_______________、_______、_______.考点3函数及其图象画函数图象的步骤:列表、________、连线.解析法(公式法)列表法图象法描点【学有奇招】 平面直角坐标系中点的坐标的特征的记忆与理解可以通过
画图来解决,实践可以加深对知识的理解和记忆.平移的特点:
左右移,纵不变,横减加;上下移,横不变,纵加减.对称点
的坐标规律:关于 x 轴对称的点,横坐标相同,纵坐标互为相
反数;关于 y 轴对称的点,纵坐标相同,横坐标互为相反数.1.点 M(-2,1)关于 y 轴对称的点的坐标是()BA.(-2,-1)
C.(2,-1)B.(2,1)
D.(1,-2)2.如果点 P(a,2)在第二象限,那么点 Q(-3,a)在()CA.第一象限
C.第三象限B.第二象限
D.第四象限3.图 3-1-2 是象棋盘的一部分,若帅位于点(1,-2)上,)C相位于点(3,-2)上,则炮位于点(
A.(-1,1) B.(-1,2)C.(-2,1)D.(-2,2)图 3-1-24.函数 y= 2
x+1的自变量的取值范围是________.x≠-1 5.如图 3-1-3,将三角形向右平移 2 个单位长度,再向上
平移 3 个单位长度,则平移后三角形的三个坐标分别是____________________. (1,7),(3,4),(-2,2)
图 3-1-3平面直角坐标系 例题:(2013 年四川雅安)在平面直角坐标系中,已知点
A(- ,0),B( ,0),点 C 在坐标轴上,且 AC+BC=6,
写出满足条件的所有点 C 的坐标______________________.
思路分析:需要分类讨论:①当点 C 位于 x 轴上时,根据
线段间的和差关系即可求得点 C 的坐标;②当点 C 位于y 轴上
时,根据勾股定理求点 C 的坐标.答案:(0,2),(0,-2),(-3,0),(3,0)图3-1-4【试题精选】
1.(2013 年辽宁大连)在平面直角坐标系中,点(2,-4)在第________象限.四 2.(2012 年山东青岛)如图 3-1-5,将四边形 ABCD 先向左
平移 3 个单位长度,再向上平移 2 个单位长度,那么点 A 的对应点 A′的坐标是()B图 3-1-5A.(6,1)
B.(0,1)
C.(0,-3)
D.(6,-3) 名师点评:在平面直角坐标系中,图形的平移与图形上某
点的平移相同.平移中点的变化规律是:横坐标右移加,左移
减;纵坐标上移加,下移减.函数自变量的取值范围 2x
x-5中,自变量 x 的取值范 3.(2013 年辽宁营口)函数 y=
围是________. 4.(2013 年辽宁铁岭)函数 y=有意义,则自变量 x的取值范围是_____________.x≥1 且 x≠2 名师点评:确定函数自变量取值范围主要看三个方面:①
分母不为0;②偶次根式的被开方数是非负数;③出现0 指数,
底数不等于 0.x≠5 函数的图象及应用
例题:(2013 年湖北鄂州)如图 3-1-6,一个大烧杯中装有一
个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)
后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后
水溢出到大烧杯中,浮子始终保持在容器的正中
间.用 x 表示注水时间,用 y 表示浮子的高度,则用来表示 y 与 x 之间关系的选项是()图 3-1-6 解析:①小烧杯未被注满,这段时间,浮子的高度快速增
加;②小烧杯被注满,大烧杯内水面的高度还未达到小烧杯的
高度,此时浮子高度不变;③大烧杯内的水面高于小烧杯,此
时浮子高度缓慢增加.结合图象可得 B 选项的图象符合.答案:B【试题精选】B 5.(2013 年辽宁营口)如图 3-1-7(1),在矩形 ABCD 中,动
点 E 从点 B 出发,沿 BADC 方向运动至点 C 处停止.设点 E
运动的路程为 x,△BCE 的面积为 y,如果 y 关于 x 的函数图象如图 3-1-7(2)所示,那么当 x=7 时,点 E 应运动到()(1)(2)A.点 C 处B.点 D 处C.点 B 处D.点 A 处图3-1-7 6.(2013 年湖南衡阳)如图3-1-8,半径为1 的圆和边长为 3
的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正
方形,设穿过时间为 t,正方形除去圆部分的面积为 s(阴影部分),则 s 与 t 的大致图象为()A图3-1-8 名师点评:解决此类题目,一要明确横、纵轴所表示的实
际意义;二要结合实际分析:当横轴上的变量逐渐增大时,纵
轴上的变量如何变化?如果变大,图象表现为上升;如果变小,
图象表现为下降;如果不变,图象表现为与横轴平行.1.(2013 年广东湛江)在平面直角坐标系中,点 A(2,-3)在第()象限.()DA.一
C.三B.二
D.四2.(2013 年广东珠海)点(3,2)关于 x 轴的对称点为()AA.(3,-2)
C.(-3,-2)B.(-3,2)
D.(2,-3)3.(2011 年广东广州)当实数 x 的取值使得 有意义时,函数 y=4x+1 中 y 的取值范围是()BA.y≥-7
C.y>9 B.y≥9
D.y≤9 4.(2013 年广东佛山)某人匀速跑步到公园,在公园某处停
留了一段时间,再沿原路匀速步行回家,此人离家的距离 y 与时间 x 的关系的大致图象是()B 5. (2012 年广东珠海)如图 3-1-9,矩形 OABC 的顶点 A、C
分别在 x 轴、y 轴的正半轴上,点 B 的坐标为(3,2),OB 与 AC
交于点 P,点 D,E,F,G 分别是线段 OP,AP,BP,CP 的中5点,则四边形 DEFG 的周长为________.
图 3-1-9 6.(2013 年广东广州)如图 3-1-10,在平面直角坐标系中,
点 O 为坐标原点,点 P 在第一象限,⊙P 与 x 轴交于 O,A 两
点,点 A 的坐标为(6,0),⊙P 的半径为 ,则点 P 的坐标为__________.图 3-1-10(3,2) 7.(2013 年广东梅州)如图 3-1-11,在平面直角坐标系中,
点 A(-2,2),B(-3,-2).
图 3-1-11
(1) 若 点 C与点 A 关于原点 O 对 称 , 则 点 C 的 坐 标 为____________;(2,-2)(2)将点 A 向右平移 5 个单位长度得到点 D,则点 D 的坐标为____________;(3,2) (3)由点 A,B,C,D 组成的四边形 ABCD 内(不包括边界)
任取一个横、纵坐标均为整数的点,求所取的点横、纵坐标之
和恰好为零的概率.
答案:由(1)、(2)可知:A(-2,2),B(-3,-2),C(2,-2),
D(3,2).∵在平行四边形 ABCD 内横、纵坐标均为整数的点有
15 个,其中横、纵坐标和为零的点有3个,即(-1,1),(0,0),(1,
同课章节目录
