2014年中考复习训练课件第五章 第2讲与圆有关的位置关系
文档属性
| 名称 | 2014年中考复习训练课件第五章 第2讲与圆有关的位置关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 532.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:44:15 | ||
图片预览








文档简介
课件27张PPT。第2讲与圆有关的位置关系 1.探索并了解点与圆、直线与圆的位置关系.
2.了解三角形的内心和外心.
3.了解切线的概念;会判定一条直线是否为圆的切线,会
过圆上一点画圆的切线.考点 1点、直线与圆的位置关系1.点与圆的位置关系.dr 设⊙O 的半径是 r,点 P 到圆心 O 的距离为 d,则有:
①______?点 P 在⊙O 内;②______?点 P 在⊙O 上;
③______?点 P 在⊙O 外.2.直线和圆的位置关系.相离相切相交d=rd圆心是三角形三边的__________的交点,这个交点叫做三角形
的__________.
2.内心:和三角形的三边都相切的圆叫做__________,其
圆心是三角形________________的交点,这个交点叫做三角形的__________.内切圆三条角平分线内心考点3切线的性质和判定1.判定定理:经过半径的外端并且垂直于这条半径的直线是圆的__________.切线垂直2.性质定理:圆的切线__________于过切点的半径.
3.经过切点并垂直于切线的直线必过圆心.【学有奇招】 1.圆的切线性质定理与它的两个推论涉及一条直线的三个
性质:①垂直于切线;②过切点;③过圆心.如果一条直线满
足以上三个条件中的任意两个,那么它一定满足另外一个条件,
可简单地理解为“知二推一”. 2.在判定直线与圆相切时,若直线与圆的公共点已知,证
题方法是“连半径,证垂直”;若直线与圆的公共点未知,证
题方法是“作垂直,证半径”.1.若线段 OA=3,⊙O 的半径为 5,则点 A 与⊙O 的位置关系为()CA.点在圆外
C.点在圆内B.点在圆上
D.不能确定2.已知⊙O 的半径为 2,直线 l 上有一点 P 满足 PO=2,D则直线 l 与⊙O 的位置关系是(
A.相切
C.相离或相切 )
B.相离
D.相切或相交3.在平面直角坐标系 xOy 中,以点(-3,4)为圆心,4 为半径的圆()CA.与 x 轴相交,与 y 轴相切
B.与 x 轴相离,与 y 轴相交
C.与 x 轴相切,与 y 轴相交
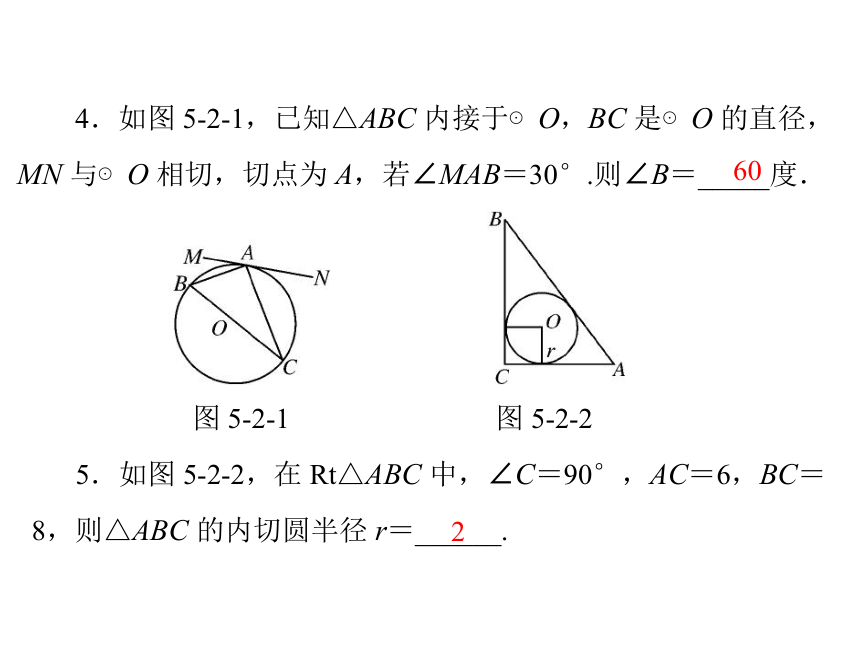
D.与 x 轴相切,与 y 轴相离 4.如图 5-2-1,已知△ABC 内接于⊙O,BC 是⊙O 的直径,
MN 与⊙O 相切,切点为 A,若∠MAB=30°.则∠B=_____度.图 5-2-1图 5-2-25.如图 5-2-2,在 Rt△ABC 中,∠C=90°,AC=6,BC=8,则△ABC 的内切圆半径 r=______.602 点、直线与圆有关的位置关系
1.(2013 年吉林)如图 5-2-3 所示,体育课上,小丽的铅球成绩为 6.4 m,她投出的铅球落在()D图 5-2-3A.区域①
B.区域②
C.区域③
D.区域④ 2.(2013 年四川凉山州)在同一平面直角坐标系中有5个点:
A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(0,-3).
(1)在图 5-2-4 中画出△ABC 的外接圆⊙P,并指出点 D 与⊙P 的位置关系; (2)若直线 l 经过点 D(-2,-2),
E(0,-3),判断直线 l 与⊙P 的位置
关系.图 5-2-4
(2)直线 l 与⊙P 相切.
理由如下:连接 PE.
∵直线 l 过点 D(-2,-2),E(0,-3),
∴PE2=12+32=10,PD2=5,DE2=5.
∴PE2=PD2+DE2.
∴△PDE 是直角三角形,且∠PDE=90°.∴PD⊥l.∴直线 l 与⊙P 相切.图26 名师点评:判断点(直线)与圆的位置关系的关键是运用点
(直线)到圆心的距离 d 和圆的半径 r 之间的数量关系进行比较. 切线的判定与性质
例题:(2013 年山东德州)如图5-2-5,已知⊙O 的半径为 1,
DE 是⊙O 的直径,过 D 作⊙O 的切线,C 是 AD 的中点,AE
交⊙O 于 B 点,四边形 BCOE 是平行四边形.
(1)求 AD 的长;
(2)BC 是⊙O 的切线吗?若是,给出证明;若不是,说明理由.图5-2-5 思路分析:(1)借助平行四边形的性质可得BC=OE=1,连
接BD,根据直角三角形斜边上的中线等于斜边的一半求解 AD;
(2) 连接BO,借助BC与OD 的位置和大小关系可知四边形
BCDO为平行四边形,再根据AD 的切线关系可得四边形BCDO
为矩形,从而得出BC 为⊙O 的切线.(2)连接OB,由(1),得BC ∥ OD,且BC=OD,
∴四边形 BCDO 是平行四边形.
又∵AD 是⊙O 的切线,∴OD⊥AD.
∴四边形 BCDO 是矩形.∴OB⊥BC.又∵OB 为⊙O 的半径,∴BC是⊙O 的切线.【试题精选】
3.(2013 年山东聊城)如图 5-2-6,AB 是⊙O 的直径,AF
是⊙O 的切线,CD 是垂直于 AB 的弦,垂足为 E,过点 C 作 ,BE=2.DA 的平行线与 AF 相交于点 F,CD=4
求证:(1)四边形 FADC 是菱形;
(2)FC 是⊙O 的切线.
图 5-2-6由垂径定理,得CE=ED=—CD=2 .解:(1)连接 OC.依题意知:AF⊥AB,又 CD⊥AB,∴AF∥CD.
又 CF∥AD,∴四边形 FADC 是平行四边形.1
2设⊙O 的半径为 R,则 OC=R,OE=OB-BE=R-2,
在 Rt△ECO 中,由勾股定理,得
R2=(R-2)2+(2 )2,解得 R=4. ∴AD=CD.因此,平行四边形 FADC 是菱形.
(2)连接 OF.由(1),得 FC=FA ,
又 OC=OA,FO=FO,
∴△FCO≌△FAO.∴∠FCO=∠FAO =90°.
因此,FC 是⊙O 的切线.
名师点评:添加有关切线辅助线的原则是:有点连半径,
证垂直;无点作垂直,证半径. 1.(2011 年广东)如图 5-2-7,AB 与⊙O 相切于点 B,AO
的延长线交⊙O于点C,连接BC.若∠A=40°,则∠C=______.图 5-2-7图 5-2-8 2.(2013 年广东梅州)如图 5-2-8,在△ABC 中,AB=2,
AC= ,以点 A 为圆心,1 为半径的圆与边 BC 相切于点 D,则∠BAC 的度数是_________.25°105°(2)若OB=5,OP= ,求 AC 的长. 3.(2013 年广东湛江)如图5-2-9,已知 AB 是⊙O 的直径,
P 为⊙O 外一点,且 OP∥BC,∠P=∠BAC.
(1)求证:PA 为⊙O 的切线;25
3图 5-2-9解:(1)设 AC 与 OP 相交于点 H.
∵AB 是直径,∴AC⊥BC,∠BAC+∠B=90°.
∵OP∥BC,∴OP⊥AC,∠AOP=∠B.
∵∠P=∠BAC,∴∠P+∠AOP=90°.
于是∠OAP=90°,∴PA 为⊙O 的切线. 4.(2013 年广东广州)已知AB 是⊙O 的直径,AB=4,点
C 在线段 AB 的延长线上运动,点 D 在⊙O 上运动(不与点 B
重合),连接 CD,且 CD=OA.(1)当 OC=2
(2)当 OC>2 时(如图 5-2-10),求证:CD 是⊙O 的切线;
时,CD 所在直线与⊙O 相交,设另一交点为 E,连
接 AE.①当 D 为 CE 中点时,求△ACE 的周长;图 5-2-10 ②连接 OD,是否存在四边形 AODE 为梯形?若存在,请
说明梯形个数并求此时 AE·ED 的值;若不存在,请说明理由.由题意可知,CD=OD=OA=—AB=2,OC=2(1)证明:如图 27(1),连接 OD. , 1
2
∴OD2+CD2=OC2.
∴△OCD 为直角三角形.则 OD⊥CD.
又∵点 D 在⊙O 上,∴CD 是⊙O 的切线.
图27 (2)解:①如图 27(2),连接 OE,OD,
则有 CD=DE=OD=OE.
∴△ODE 为等边三角形,∠1=∠2=∠3=60°.
∵OD=CD,∴∠4=∠5.
∵∠3=∠4+∠5,∴∠4=∠5=30°.
∴∠EOC=∠2+∠4=90°.
因此△EOC 是含 30 度角的直角三角形,△AOE 是等腰直
角三角形.∵在 Rt△EOC 中,CE=2OA=4,OC=4cos30°=2 ②存在,这样的梯形有 2 个.
图 27(3)是 D 点位于 AB 上方的情形,同理在 AB 下方还有
一个梯形,它们关于直线 AB 成轴对称.
∵OA=OE,∴∠1=∠2.
∵CD=OA=OD,∴∠4=∠5.
∵四边形 AODE 为梯形,=,∴CE·DE=OE2=22=4.∴OD∥AE,∴∠4=∠1,∠3=∠2.∴∠3=∠5=∠1.
在△ODE 与△COE 中,∠OED=∠OEC,∠3=∠5,
∴△ODE∽△COE.则有OE DE
CE OE ∵∠1=∠5,∴AE=CE.
∴AE·DE=CE·DE=4.
综上所述,存在四边形 AODE 为梯形,这样的梯形有 2 个,
此时 AE·DE=4.
2.了解三角形的内心和外心.
3.了解切线的概念;会判定一条直线是否为圆的切线,会
过圆上一点画圆的切线.考点 1点、直线与圆的位置关系1.点与圆的位置关系.d
①______?点 P 在⊙O 内;②______?点 P 在⊙O 上;
③______?点 P 在⊙O 外.2.直线和圆的位置关系.相离相切相交d=rd
的__________.
2.内心:和三角形的三边都相切的圆叫做__________,其
圆心是三角形________________的交点,这个交点叫做三角形的__________.内切圆三条角平分线内心考点3切线的性质和判定1.判定定理:经过半径的外端并且垂直于这条半径的直线是圆的__________.切线垂直2.性质定理:圆的切线__________于过切点的半径.
3.经过切点并垂直于切线的直线必过圆心.【学有奇招】 1.圆的切线性质定理与它的两个推论涉及一条直线的三个
性质:①垂直于切线;②过切点;③过圆心.如果一条直线满
足以上三个条件中的任意两个,那么它一定满足另外一个条件,
可简单地理解为“知二推一”. 2.在判定直线与圆相切时,若直线与圆的公共点已知,证
题方法是“连半径,证垂直”;若直线与圆的公共点未知,证
题方法是“作垂直,证半径”.1.若线段 OA=3,⊙O 的半径为 5,则点 A 与⊙O 的位置关系为()CA.点在圆外
C.点在圆内B.点在圆上
D.不能确定2.已知⊙O 的半径为 2,直线 l 上有一点 P 满足 PO=2,D则直线 l 与⊙O 的位置关系是(
A.相切
C.相离或相切 )
B.相离
D.相切或相交3.在平面直角坐标系 xOy 中,以点(-3,4)为圆心,4 为半径的圆()CA.与 x 轴相交,与 y 轴相切
B.与 x 轴相离,与 y 轴相交
C.与 x 轴相切,与 y 轴相交
D.与 x 轴相切,与 y 轴相离 4.如图 5-2-1,已知△ABC 内接于⊙O,BC 是⊙O 的直径,
MN 与⊙O 相切,切点为 A,若∠MAB=30°.则∠B=_____度.图 5-2-1图 5-2-25.如图 5-2-2,在 Rt△ABC 中,∠C=90°,AC=6,BC=8,则△ABC 的内切圆半径 r=______.602 点、直线与圆有关的位置关系
1.(2013 年吉林)如图 5-2-3 所示,体育课上,小丽的铅球成绩为 6.4 m,她投出的铅球落在()D图 5-2-3A.区域①
B.区域②
C.区域③
D.区域④ 2.(2013 年四川凉山州)在同一平面直角坐标系中有5个点:
A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(0,-3).
(1)在图 5-2-4 中画出△ABC 的外接圆⊙P,并指出点 D 与⊙P 的位置关系; (2)若直线 l 经过点 D(-2,-2),
E(0,-3),判断直线 l 与⊙P 的位置
关系.图 5-2-4
(2)直线 l 与⊙P 相切.
理由如下:连接 PE.
∵直线 l 过点 D(-2,-2),E(0,-3),
∴PE2=12+32=10,PD2=5,DE2=5.
∴PE2=PD2+DE2.
∴△PDE 是直角三角形,且∠PDE=90°.∴PD⊥l.∴直线 l 与⊙P 相切.图26 名师点评:判断点(直线)与圆的位置关系的关键是运用点
(直线)到圆心的距离 d 和圆的半径 r 之间的数量关系进行比较. 切线的判定与性质
例题:(2013 年山东德州)如图5-2-5,已知⊙O 的半径为 1,
DE 是⊙O 的直径,过 D 作⊙O 的切线,C 是 AD 的中点,AE
交⊙O 于 B 点,四边形 BCOE 是平行四边形.
(1)求 AD 的长;
(2)BC 是⊙O 的切线吗?若是,给出证明;若不是,说明理由.图5-2-5 思路分析:(1)借助平行四边形的性质可得BC=OE=1,连
接BD,根据直角三角形斜边上的中线等于斜边的一半求解 AD;
(2) 连接BO,借助BC与OD 的位置和大小关系可知四边形
BCDO为平行四边形,再根据AD 的切线关系可得四边形BCDO
为矩形,从而得出BC 为⊙O 的切线.(2)连接OB,由(1),得BC ∥ OD,且BC=OD,
∴四边形 BCDO 是平行四边形.
又∵AD 是⊙O 的切线,∴OD⊥AD.
∴四边形 BCDO 是矩形.∴OB⊥BC.又∵OB 为⊙O 的半径,∴BC是⊙O 的切线.【试题精选】
3.(2013 年山东聊城)如图 5-2-6,AB 是⊙O 的直径,AF
是⊙O 的切线,CD 是垂直于 AB 的弦,垂足为 E,过点 C 作 ,BE=2.DA 的平行线与 AF 相交于点 F,CD=4
求证:(1)四边形 FADC 是菱形;
(2)FC 是⊙O 的切线.
图 5-2-6由垂径定理,得CE=ED=—CD=2 .解:(1)连接 OC.依题意知:AF⊥AB,又 CD⊥AB,∴AF∥CD.
又 CF∥AD,∴四边形 FADC 是平行四边形.1
2设⊙O 的半径为 R,则 OC=R,OE=OB-BE=R-2,
在 Rt△ECO 中,由勾股定理,得
R2=(R-2)2+(2 )2,解得 R=4. ∴AD=CD.因此,平行四边形 FADC 是菱形.
(2)连接 OF.由(1),得 FC=FA ,
又 OC=OA,FO=FO,
∴△FCO≌△FAO.∴∠FCO=∠FAO =90°.
因此,FC 是⊙O 的切线.
名师点评:添加有关切线辅助线的原则是:有点连半径,
证垂直;无点作垂直,证半径. 1.(2011 年广东)如图 5-2-7,AB 与⊙O 相切于点 B,AO
的延长线交⊙O于点C,连接BC.若∠A=40°,则∠C=______.图 5-2-7图 5-2-8 2.(2013 年广东梅州)如图 5-2-8,在△ABC 中,AB=2,
AC= ,以点 A 为圆心,1 为半径的圆与边 BC 相切于点 D,则∠BAC 的度数是_________.25°105°(2)若OB=5,OP= ,求 AC 的长. 3.(2013 年广东湛江)如图5-2-9,已知 AB 是⊙O 的直径,
P 为⊙O 外一点,且 OP∥BC,∠P=∠BAC.
(1)求证:PA 为⊙O 的切线;25
3图 5-2-9解:(1)设 AC 与 OP 相交于点 H.
∵AB 是直径,∴AC⊥BC,∠BAC+∠B=90°.
∵OP∥BC,∴OP⊥AC,∠AOP=∠B.
∵∠P=∠BAC,∴∠P+∠AOP=90°.
于是∠OAP=90°,∴PA 为⊙O 的切线. 4.(2013 年广东广州)已知AB 是⊙O 的直径,AB=4,点
C 在线段 AB 的延长线上运动,点 D 在⊙O 上运动(不与点 B
重合),连接 CD,且 CD=OA.(1)当 OC=2
(2)当 OC>2 时(如图 5-2-10),求证:CD 是⊙O 的切线;
时,CD 所在直线与⊙O 相交,设另一交点为 E,连
接 AE.①当 D 为 CE 中点时,求△ACE 的周长;图 5-2-10 ②连接 OD,是否存在四边形 AODE 为梯形?若存在,请
说明梯形个数并求此时 AE·ED 的值;若不存在,请说明理由.由题意可知,CD=OD=OA=—AB=2,OC=2(1)证明:如图 27(1),连接 OD. , 1
2
∴OD2+CD2=OC2.
∴△OCD 为直角三角形.则 OD⊥CD.
又∵点 D 在⊙O 上,∴CD 是⊙O 的切线.
图27 (2)解:①如图 27(2),连接 OE,OD,
则有 CD=DE=OD=OE.
∴△ODE 为等边三角形,∠1=∠2=∠3=60°.
∵OD=CD,∴∠4=∠5.
∵∠3=∠4+∠5,∴∠4=∠5=30°.
∴∠EOC=∠2+∠4=90°.
因此△EOC 是含 30 度角的直角三角形,△AOE 是等腰直
角三角形.∵在 Rt△EOC 中,CE=2OA=4,OC=4cos30°=2 ②存在,这样的梯形有 2 个.
图 27(3)是 D 点位于 AB 上方的情形,同理在 AB 下方还有
一个梯形,它们关于直线 AB 成轴对称.
∵OA=OE,∴∠1=∠2.
∵CD=OA=OD,∴∠4=∠5.
∵四边形 AODE 为梯形,=,∴CE·DE=OE2=22=4.∴OD∥AE,∴∠4=∠1,∠3=∠2.∴∠3=∠5=∠1.
在△ODE 与△COE 中,∠OED=∠OEC,∠3=∠5,
∴△ODE∽△COE.则有OE DE
CE OE ∵∠1=∠5,∴AE=CE.
∴AE·DE=CE·DE=4.
综上所述,存在四边形 AODE 为梯形,这样的梯形有 2 个,
此时 AE·DE=4.
同课章节目录
