2014年中考数学总复习提能训练课件第六章 第3讲尺规作图
文档属性
| 名称 | 2014年中考数学总复习提能训练课件第六章 第3讲尺规作图 |

|
|
| 格式 | zip | ||
| 文件大小 | 360.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 00:00:00 | ||
图片预览






文档简介
课件18张PPT。第3讲尺规作图 1.完成以下基本作图:作一条线段等于已知线段,作一个
角等于已知角,作角的平分线,作线段的垂直平分线.
2.利用基本作图作三角形:已知三边作三角形;已知两边
及其夹角作三角形;已知两角及其夹边作三角形;已知底边及
底边上的高作等腰三角形.
3.了解如何过一点、两点和不在同一条直线上的三点作圆.
4.了解尺规作图的步骤(不要求作法).考点尺规作图及基本作图 1.定义:在几何里,把限定用__________的直尺和_____
来画图称为尺规作图.2.五种基本作图.没有刻度圆规 (1)作一条线段等于已知线段.(2)作一个角等于已知角.(3)
作一个角的平分线.(4)过定点作已知直线的垂线.(5)作线段的
垂直平分线.3.作图的一般步骤.(1)已知.(2)求作.(3)作法. 注意:当不要求写作法时,一般要保留作图痕迹.对于较
复杂的作图,可先画出草图,使它同所要作的图大致相同,然
后借助草图寻找作法.
【学有奇招】 尺规作图通常需要考生保留作图痕迹,并以此作为考查考
生的作图是否正确的依据,所以在考试时注意保留清晰的作图
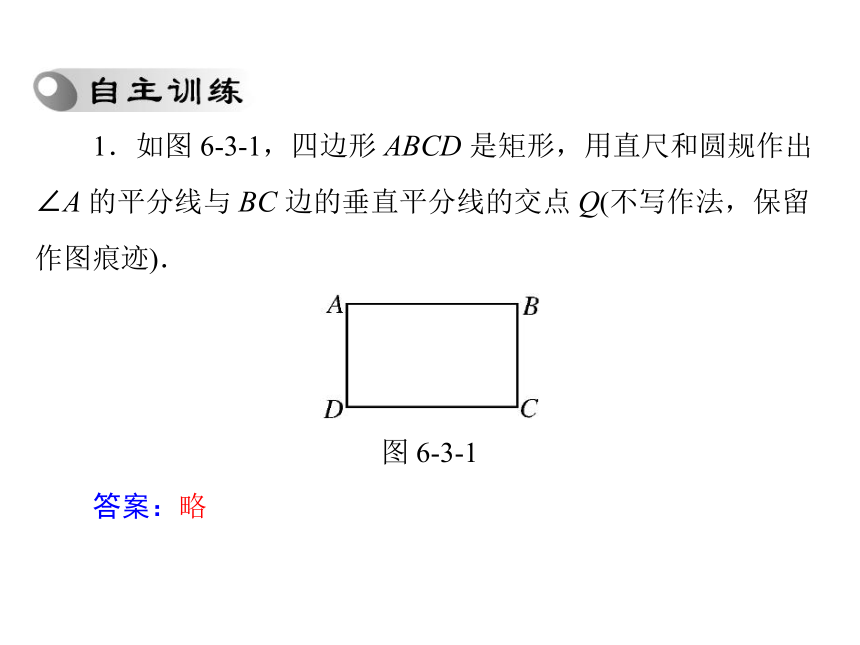
痕迹是得分的技巧之一. 1.如图 6-3-1,四边形 ABCD 是矩形,用直尺和圆规作出
∠A 的平分线与 BC 边的垂直平分线的交点 Q(不写作法,保留
作图痕迹).图 6-3-1答案:略2.已知:如图 6-3-2,直线 AB 与直线 BC 相交于点 B,点D 是直线 BC 上一点.求作:点 E,使直线 DE∥AB,且点 E 到 B,D 两点距离相等(在题目的原图中完成作图).图 6-3-2答案:略基本作图与应用 例题:(2013 年甘肃兰州)如图 6-3-3,两条公路 OA 和 OB
相交于 O 点,在∠AOB 的内部有工厂 C 和 D,现要修建一个货
站 P 到两条公路 OA,OB 的距离相等,且到两工厂 C,D 的距
离相等,用尺规作出货站 P 的位置(要求:不写作法,保留作图
痕迹,写出结论).图6-3-3 思路分析:根据角平分线上的点到角的两边的距离相等,
线段垂直平分线上的点到线段两端点距离相等,作∠AOB 的平
分线与 CD 的垂直平分线,交点就是货站 P 的位置.
解:如图6-3-4,作∠AOB 的平分线OH,CD 的垂直平分
线EF,OH 与EF 的交点P 就是货站的位置. 所以点P 就是所
要求作的点.图 6-3-4【试题精选】
1.(2013 年江苏南通)如图6-3-5,用尺规作出∠OBF=∠AOB,作图痕迹 是()D图 6-3-5A. 以点 B 为圆心,OD 为半径的弧
B. 以点 B 为圆心,DC 为半径的弧
C. 以点 E 为圆心,OD 为半径的弧
D. 以点 E 为圆心,DC 为半径的弧作图与证明 2.(2013 年浙江嘉兴)小明在做课本“目标与评定”中的一
道题:如图 6-3-6(1),直线 a,b 所成的角跑到画板外面去了,
你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图 6-3-6(2),画 PC∥a,量出直线 b 与PC 的夹角度数,即直线 a,b 所成角的度数.(1)请写出这种做法的理由; (2)小明在此基础上又进行了如下操作和探究 [ 如 图
6-3-6(3)]:①以P为圆心,任意长为半径画圆弧,分别交直线 b,PC 于点 A,D;②连接 AD 并延长交直线 a 于点 B,请写出图
6-3-6(3)中所有与∠PAB 相等的角,并说明理由;
(3)请在图 6-3-6(3)画板内作出“直线 a,b 所成的跑到画板
外面去的角”的平分线(画板内的部分),只要求作出图形,并
保留作图痕迹.(1)(2)(3)图6-3-6解:(1)PC∥a(两直线平行,同位角相等).
(2)如图 45,∠PAB=∠PDA=∠BDC=∠1.
∵PA =PD,∴∠PAB=∠PDA.
∵PC∥a,∴∠PDA=∠1.
∴∠PAB=∠PDA=∠BDC=∠1 .(3)如图 45,EF 是所求作的图形.图 45 名师点评:中考通常以基本的尺规作图为载体,在具体情
境中酝酿与构建图形之间的形状、位置、大小关系,进而对相
关问题进行计算、探究、发现与证明.1.(2013 年广东)如图 6-3-7,已知?ABCD. (1)作图:延长 BC,并在 BC 的延长线上截取线段 CE,使
得 CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接 AE,交 CD 于点F ,求证:△AFD≌△EFC.图 6-3-7 (1)解:延长 BC,以点 C 为圆心,以BC为长画弧,交 BC
延长线于点 E,如图 46,线段 CE 为所求.
(2)证明:在?ABCD 中,AD∥BC,AD=BC,
∴∠DAF=∠CEF.
∵CE=BC,∴AD=CE.
又∵∠DFA=∠CFE,∴△AFD≌△EFC.图 46 2.(2013 年广东广州)已知四边形 ABCD 是平行四边形(如
图 6-3-8),把△ABD 沿对角线 BD 翻折 180°得到△A′BD.
(1)利用尺规作出△A′BD(要求保留作图痕迹,不写作法);
(2)设 DA′与 BC 交于点 E,求证:图 6-3-8△BA′E≌△DCE. 解:(1)如图47, △A′BD 即为所求.
(2)因为四边形 ABCD 是平行四边形,
所以∠A=∠C,AB=CD.
又由作图可知∠A′=∠A=∠C,BA′=DC.
在△BA′E 和△DCE 中,
∠A′=∠C,
∠BEA′=∠DEC,
BA′=DC,∴ △ BA′E≌ △DCE.图 47 3.(2012 年广东梅州)如图 6-3-9,已知△ABC,按如下步
骤作图:
1
2
边作弧,交于 M,N 两点;
②连接 MN,分别交 AB,AC 于
点 D,O;
③过点 C 作 CE∥AB 交 MN 于点 E,连接 AE,CD.
(1)求证:四边形 ADCE 是菱形;
(2)当∠ACB=90°,BC=6,△ADC 的周长为 18 时,求四边形 ADCE 的面积.图 6-3-9①分别以 A,C 为圆心,以大于—AC的长为半径在AC两边 == .(1)证明:由题意可知:
∵直线 DE 是线段 AC 的垂直平分线,
∴AC⊥DE,即∠AOD=∠COE=90°.
且 AD=CD,AO=CO.
又∵CE∥AB,∴∠ADO=∠OEC.
∴△AOD≌△COE.
∴OD=OE.∴四边形 ADCE 是菱形.
(2)解:当∠ACB=90°时,OD∥BC,即有△ADO∽△ABC,∴OD AO 1
BC AC 2
角等于已知角,作角的平分线,作线段的垂直平分线.
2.利用基本作图作三角形:已知三边作三角形;已知两边
及其夹角作三角形;已知两角及其夹边作三角形;已知底边及
底边上的高作等腰三角形.
3.了解如何过一点、两点和不在同一条直线上的三点作圆.
4.了解尺规作图的步骤(不要求作法).考点尺规作图及基本作图 1.定义:在几何里,把限定用__________的直尺和_____
来画图称为尺规作图.2.五种基本作图.没有刻度圆规 (1)作一条线段等于已知线段.(2)作一个角等于已知角.(3)
作一个角的平分线.(4)过定点作已知直线的垂线.(5)作线段的
垂直平分线.3.作图的一般步骤.(1)已知.(2)求作.(3)作法. 注意:当不要求写作法时,一般要保留作图痕迹.对于较
复杂的作图,可先画出草图,使它同所要作的图大致相同,然
后借助草图寻找作法.
【学有奇招】 尺规作图通常需要考生保留作图痕迹,并以此作为考查考
生的作图是否正确的依据,所以在考试时注意保留清晰的作图
痕迹是得分的技巧之一. 1.如图 6-3-1,四边形 ABCD 是矩形,用直尺和圆规作出
∠A 的平分线与 BC 边的垂直平分线的交点 Q(不写作法,保留
作图痕迹).图 6-3-1答案:略2.已知:如图 6-3-2,直线 AB 与直线 BC 相交于点 B,点D 是直线 BC 上一点.求作:点 E,使直线 DE∥AB,且点 E 到 B,D 两点距离相等(在题目的原图中完成作图).图 6-3-2答案:略基本作图与应用 例题:(2013 年甘肃兰州)如图 6-3-3,两条公路 OA 和 OB
相交于 O 点,在∠AOB 的内部有工厂 C 和 D,现要修建一个货
站 P 到两条公路 OA,OB 的距离相等,且到两工厂 C,D 的距
离相等,用尺规作出货站 P 的位置(要求:不写作法,保留作图
痕迹,写出结论).图6-3-3 思路分析:根据角平分线上的点到角的两边的距离相等,
线段垂直平分线上的点到线段两端点距离相等,作∠AOB 的平
分线与 CD 的垂直平分线,交点就是货站 P 的位置.
解:如图6-3-4,作∠AOB 的平分线OH,CD 的垂直平分
线EF,OH 与EF 的交点P 就是货站的位置. 所以点P 就是所
要求作的点.图 6-3-4【试题精选】
1.(2013 年江苏南通)如图6-3-5,用尺规作出∠OBF=∠AOB,作图痕迹 是()D图 6-3-5A. 以点 B 为圆心,OD 为半径的弧
B. 以点 B 为圆心,DC 为半径的弧
C. 以点 E 为圆心,OD 为半径的弧
D. 以点 E 为圆心,DC 为半径的弧作图与证明 2.(2013 年浙江嘉兴)小明在做课本“目标与评定”中的一
道题:如图 6-3-6(1),直线 a,b 所成的角跑到画板外面去了,
你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图 6-3-6(2),画 PC∥a,量出直线 b 与PC 的夹角度数,即直线 a,b 所成角的度数.(1)请写出这种做法的理由; (2)小明在此基础上又进行了如下操作和探究 [ 如 图
6-3-6(3)]:①以P为圆心,任意长为半径画圆弧,分别交直线 b,PC 于点 A,D;②连接 AD 并延长交直线 a 于点 B,请写出图
6-3-6(3)中所有与∠PAB 相等的角,并说明理由;
(3)请在图 6-3-6(3)画板内作出“直线 a,b 所成的跑到画板
外面去的角”的平分线(画板内的部分),只要求作出图形,并
保留作图痕迹.(1)(2)(3)图6-3-6解:(1)PC∥a(两直线平行,同位角相等).
(2)如图 45,∠PAB=∠PDA=∠BDC=∠1.
∵PA =PD,∴∠PAB=∠PDA.
∵PC∥a,∴∠PDA=∠1.
∴∠PAB=∠PDA=∠BDC=∠1 .(3)如图 45,EF 是所求作的图形.图 45 名师点评:中考通常以基本的尺规作图为载体,在具体情
境中酝酿与构建图形之间的形状、位置、大小关系,进而对相
关问题进行计算、探究、发现与证明.1.(2013 年广东)如图 6-3-7,已知?ABCD. (1)作图:延长 BC,并在 BC 的延长线上截取线段 CE,使
得 CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接 AE,交 CD 于点F ,求证:△AFD≌△EFC.图 6-3-7 (1)解:延长 BC,以点 C 为圆心,以BC为长画弧,交 BC
延长线于点 E,如图 46,线段 CE 为所求.
(2)证明:在?ABCD 中,AD∥BC,AD=BC,
∴∠DAF=∠CEF.
∵CE=BC,∴AD=CE.
又∵∠DFA=∠CFE,∴△AFD≌△EFC.图 46 2.(2013 年广东广州)已知四边形 ABCD 是平行四边形(如
图 6-3-8),把△ABD 沿对角线 BD 翻折 180°得到△A′BD.
(1)利用尺规作出△A′BD(要求保留作图痕迹,不写作法);
(2)设 DA′与 BC 交于点 E,求证:图 6-3-8△BA′E≌△DCE. 解:(1)如图47, △A′BD 即为所求.
(2)因为四边形 ABCD 是平行四边形,
所以∠A=∠C,AB=CD.
又由作图可知∠A′=∠A=∠C,BA′=DC.
在△BA′E 和△DCE 中,
∠A′=∠C,
∠BEA′=∠DEC,
BA′=DC,∴ △ BA′E≌ △DCE.图 47 3.(2012 年广东梅州)如图 6-3-9,已知△ABC,按如下步
骤作图:
1
2
边作弧,交于 M,N 两点;
②连接 MN,分别交 AB,AC 于
点 D,O;
③过点 C 作 CE∥AB 交 MN 于点 E,连接 AE,CD.
(1)求证:四边形 ADCE 是菱形;
(2)当∠ACB=90°,BC=6,△ADC 的周长为 18 时,求四边形 ADCE 的面积.图 6-3-9①分别以 A,C 为圆心,以大于—AC的长为半径在AC两边 == .(1)证明:由题意可知:
∵直线 DE 是线段 AC 的垂直平分线,
∴AC⊥DE,即∠AOD=∠COE=90°.
且 AD=CD,AO=CO.
又∵CE∥AB,∴∠ADO=∠OEC.
∴△AOD≌△COE.
∴OD=OE.∴四边形 ADCE 是菱形.
(2)解:当∠ACB=90°时,OD∥BC,即有△ADO∽△ABC,∴OD AO 1
BC AC 2
同课章节目录
