2014年中考数学总复习提能训练课件第七章 第1讲统计
文档属性
| 名称 | 2014年中考数学总复习提能训练课件第七章 第1讲统计 |

|
|
| 格式 | zip | ||
| 文件大小 | 578.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:49:16 | ||
图片预览










文档简介
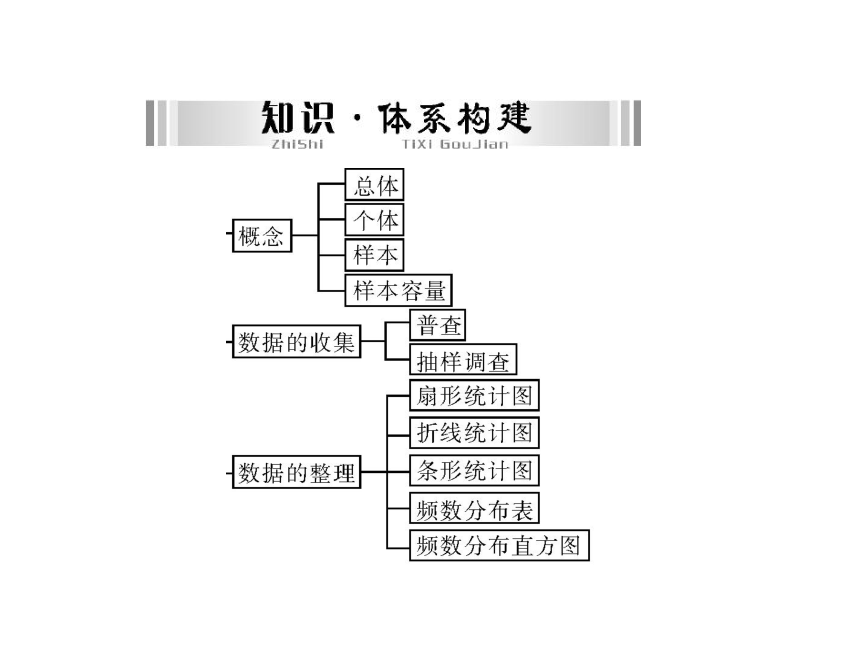
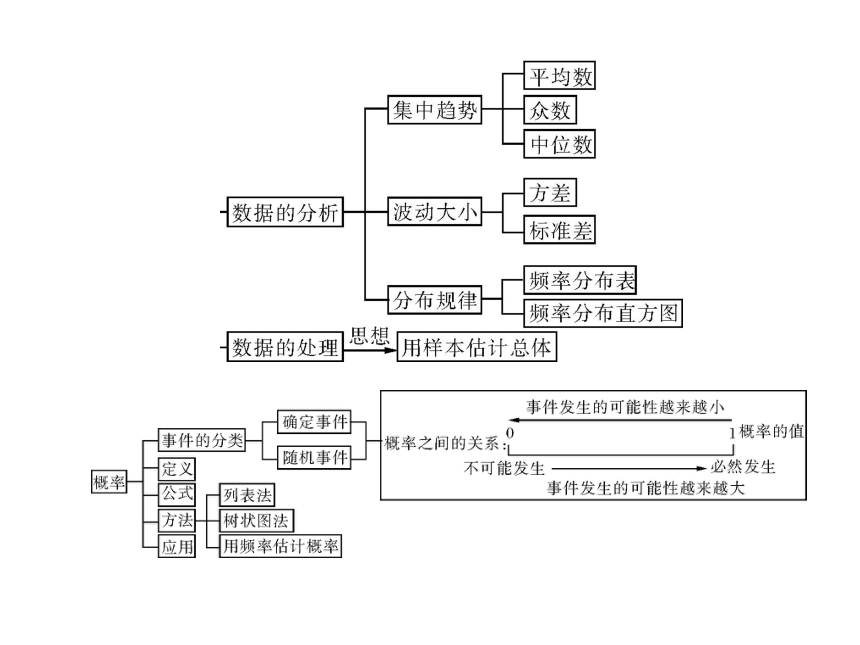
课件32张PPT。第七章 统计与概率第1讲 统计1.从事收集、整理、描述和分析数据的活动,能用计算器处理较为复杂的统计数据.2.能指出总体、个体、样本,体会不同的抽样可能得到不同的结果.3.会用扇形统计图表示数据.4.在具体情境中理解并会计算加权平均数;根据具体问题,能选择合适的统计量表示数据的集中程度.5.会计算方差,并会用它们表示数据的离散程度. 6.通过实例,理解频数、频率的概念,了解频数分布的意
义和作用,会列频数分布表,画频数分布直方图,并能解决简
单的实际问题.7.通过实例,体会用样本估计总体的思想,能用样本的平均数、方差来估计总体的平均数和方差. 8.根据统计结果作出合理的判断和预测,体会统计对决策
的作用,能比较清晰地表达自己的观点,并进行交流.
9.能根据问题查找有关资料,获得数据信息;对日常生活中的某些数据发表自己的看法.10.认识到统计在社会生活及科学领域中的应用,并能解决一些简单的实际问题.考点 1数据收集普查抽样调查 1.数据收集常用方法:________、__________.
2.收集数据时常见的统计量有:总体、个体、样本、样本
容量.
(1)总体:要考察的全体对象.(2)个体:组成总体的每一个
考察对象.(3)样本:被抽查的那些个体组成一个样本.(4)样本
容量:样本中个体的数目.考点2数据的分析 1.反映数据集中程度的量.
(1)平均数: x1,x2,…,xn的平均数x =__________________.
加权平均数:若 x1 出现 f1 次,x2 出现 f2 次,…,xk 出现 fk
次 , 且 f1 + f2 + … + fk = n , 则这k个数的加权平均数 x =________________________.中间 (2)中位数:一组数据按从小到大(或从大到小)的顺序排列,
处于最_____位置的一个数据(或最中间的两个数据的平均数).(3)众数:一组数据中出现次数________的数据.最多 2.反映数据离散程度的量.
(1)极差:最大数-最小数.
(2)方差:①公式:设 x1,x2,…,xn 的平均数为 x ,则这 n
个数据的方差为 s2=___________________________________;
②方差越大,数据的波动越大;方差越小,数据的波动越小.考点3数据的整理和描述1.频数、频率.次数比(1)频数:每个对象出现的__________.
(2)频率:频数与数据总数的________.2.统计图.条形统计扇形统计折线统计(1)________________图能够显示每组中的具体数据.
(2)________________图能够显示部分在总体中的百分比.
(3)________________图能够显示数据的变化趋势.
(4)________________图能够显示数据的分布情况.频数分布直方3.画频数分布直方图的步骤. (1)计算最大值与最小值的差;(2)决定组距与组数;(3)列频
数分布表;(4)画频数分布直方图.
【学有奇招】
数据的整理和描述解题技巧为“找对应,选公式,会估
计”.具体步骤如下:①从统计表和统计图中寻找突破点:对
应的频数、总数、频率;②灵活选用公式:①频数=总数x频
率,②频数之和=总数,③频率之和=1;③会用样本估计总体. 1.下列四种调查:
①调查某班学生的身高情况;②调查某城市的空气质量;
③调查某风景区全年的游客流量;④调查某批汽车的抗撞击能力.其中适合用全面调查方式的是()AA.①B.②C.③D.④ 2.为了解我市七年级学生的身高,从中抽取了 500 名学生,
对其身高进行统计分析,样本是___________________.
500 名学生的身高 3.七年级(1)班与(2)班各选出 20 名学生进行英文打字比赛,
通过对参赛学生每分钟输入的单词个数进行统计,两班成绩的
平均数相同,(1)班成绩的方差为 17.5,(2)班成绩的方差为 15.由此可知________班的成绩更稳定.(2)4.九(1)班参加乒乓球兴趣小组的 15 人身高如下表所示:
他们身高的中位数是__________;众数是________;平均数是________(精确到 0.01).1.701.621.66 求反映数据集中程度的量:平均数、众数、中位数
1.(2013 年广东茂名)商店某天销售了 13 双运动鞋,其尺
码统计如下表:则这 13 双运动鞋尺码的众数和中位数分别是()AA.39 码、39 码
C.40 码、39 码B.39 码、40 码
D.40 码、40 码2.(2013 年福建福州)某校女子排球队队员的年龄分布如下表:则该校女子排球队队员的平均年龄是________岁.14+14×7+15×4)=14(岁).
名师点评:(1)中位数的找法切记先排序,再找中.(2)求加
权平均数找“权”很关键,具体方法为:第 2 题中有两个量,
年龄和人数,问题是求年龄的平均数,人数则为“权”. 解决有关整理和描述数据的频数、频率与统计图问题
例题:(2013 年甘肃兰州)在兰州市开展的“体育、艺术 2
+1”活动中,某校根据实际情况,决定主要开设 A:乒乓球,
B:篮球,C:跑步,D:跳绳,这四种运动项目.为了解学生
喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结
果绘制成如图 7-1-1(1)(2)所示的条形统计图和扇形统计图.请
你结合图中的信息解答下列问题:(1)(2)图7-1-1(1)样本中喜欢 B 项目的人数百分比是______________,其所在扇形统计图中的圆心角的度数是________;(2)把条形统计图补充完整;(3)已知该校有 1000 人,根据样本估计全校喜欢乒乓球的人数是多少?解:(1)1-44%-8%-28%=20%,其所在扇形统计图中的圆心角的度数是:
360°×20%=72°.(2)调查的总人数是:44÷44%=100(人),
则喜欢B 的人数是:100×20%=20(人).
补全条形统计图如图 7-1-2.图 7-1-2(3)全校喜欢乒乓球的人数是1000×44%=440(人).【试题精选】
3.(2013 年河南)从 2013 年 1 月 7 日起,中国中东部大部
分地区持续出现雾霾天气.某市记者为了解雾霾天气的主要原
因,随机调查了该市部分市民,并对调查结果进行整理.绘制了如图 7-1-3 所示的尚不完整的统计图表.图 7-1-3= .请根据图表中提供的信息解答下列问题:
(1)填空:m=________,n=________.扇形统计图中 E 组所占的百分比为________%;4010015 (2)若该市人口约有 100 万人,请你估计其中持 D 组“观
点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查 1 人,则此人持
C 组“观点”的概率是多少?解:(2)100×120
400=30(万人).(3)随机抽查 1 人,则此人持 C 组“观点”的概率是100 1
400 4 名师点评:这类题目通常把各种统计图、统计表结合起来
解决频率、频数问题.“找对应,选公式,会估计”就是解题
技巧. 1.(2012 年广东佛山)吸烟有害健康,被动吸烟也有害健康.
如果要了解人们被动吸烟的情况,那么最合适的调查方式是()A.普查BB.抽样调查
C.在社会上随机调查
D.在学校里随机调查2.(2013 年广东汕头)数学 1,2,5,3,5,3,3 的中位数是()A.1B.2C.3D.5C 3.(2013 年广东茂名)小李和小林练习射箭,射完 10 箭后
两人的成绩如图 7-1-4,通常新手的成绩不太稳定,根据图中的小李信息,估计这两人中的新手是__________.
图 7-1-48.58.50.156 4.(2012 年广东梅州)为参加 2012 年“梅州市实践毕业生
升学体育考试”,小峰同学进行了刻苦训练,在投掷实心球时,
测得 5 次投掷的成绩(单位:m)8,8.5,8.8,8.5,9.2.这组数据的:
①众数是_____;②中位数是____;③方差是______. 5.(2013 年广东深圳)2013 年起,深圳市实施行人闯红灯
违法处罚 , 处罚方式分为四类 : “ 罚 款 20 元 ”“ 罚 款 50
元”“罚款 100 元”“穿绿马甲维护交通”.图 7-1-5 是实施
首日由某片区的执法结果整理数据后绘制的两幅不完整的统计
图,请你根据图中提供的信息,解答下列问题:
(1)实施首日,该片区行人闯红灯违法受处罚一共_____人;
(2)在所有闯红灯违法受处罚的行人中,穿绿马甲维护交通所占的百分比是________%;20065(3)据了解,“罚款 20 元”人数是“罚款 50 元”人数的 2倍,请补全条形统计图;解:补全条形统计图如图 63.图 63(4)根据(3)中的信息,在扇形统计图中,“罚款 20 元”所72在扇形的圆心角等于________度.
图7-1-5 6.(2013 年广东)某校教导处为了解该校七年级同学对排
球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情
况(每位同学必须且只能选择最喜爱的一项运动项目),进行了
随机抽样调查,并将调查结果统计后绘制成如图 7-1-6 所示的
不完整统计图表.(1)请你补全下列样本人数分布表和条形统计图;(2)若七年级学生总人数为 920 人,请你估计七年级学生喜爱羽毛球运动项目的人数.样本人数分布表图7-1-6解:补全人数分布表如下:补全条形统计图如图64.图 64(2)920×30%=276(人).
七年级学生喜爱羽毛球运动项目的人数为 276 人. 7.(2012 年广东湛江)2013 年3月28日是全国中小学生安
全教育日,某学校为加强学生的安全意识,组织了全校 1500 名
学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整
数,满分为 100 分)进行统计.请根据尚未完成的频率分布表和图7-1-7频数分布直方图(如图 7-1-7),解答下列问题:
频率分布表(1)这次抽取了__________名学生的竞赛成绩进行统计,其中:m=__________,n=________;200700.12 (2)补全频数分布直方图;
(3)若成绩在 70 分以下(含 70 分)的学生为安全意识不强,
有待进一步加强安全教育,则该校
安全意识不强的学生约有多少人?解:(2)如图65.图65(3)1500×(0.2+0.08)=420(人).
义和作用,会列频数分布表,画频数分布直方图,并能解决简
单的实际问题.7.通过实例,体会用样本估计总体的思想,能用样本的平均数、方差来估计总体的平均数和方差. 8.根据统计结果作出合理的判断和预测,体会统计对决策
的作用,能比较清晰地表达自己的观点,并进行交流.
9.能根据问题查找有关资料,获得数据信息;对日常生活中的某些数据发表自己的看法.10.认识到统计在社会生活及科学领域中的应用,并能解决一些简单的实际问题.考点 1数据收集普查抽样调查 1.数据收集常用方法:________、__________.
2.收集数据时常见的统计量有:总体、个体、样本、样本
容量.
(1)总体:要考察的全体对象.(2)个体:组成总体的每一个
考察对象.(3)样本:被抽查的那些个体组成一个样本.(4)样本
容量:样本中个体的数目.考点2数据的分析 1.反映数据集中程度的量.
(1)平均数: x1,x2,…,xn的平均数x =__________________.
加权平均数:若 x1 出现 f1 次,x2 出现 f2 次,…,xk 出现 fk
次 , 且 f1 + f2 + … + fk = n , 则这k个数的加权平均数 x =________________________.中间 (2)中位数:一组数据按从小到大(或从大到小)的顺序排列,
处于最_____位置的一个数据(或最中间的两个数据的平均数).(3)众数:一组数据中出现次数________的数据.最多 2.反映数据离散程度的量.
(1)极差:最大数-最小数.
(2)方差:①公式:设 x1,x2,…,xn 的平均数为 x ,则这 n
个数据的方差为 s2=___________________________________;
②方差越大,数据的波动越大;方差越小,数据的波动越小.考点3数据的整理和描述1.频数、频率.次数比(1)频数:每个对象出现的__________.
(2)频率:频数与数据总数的________.2.统计图.条形统计扇形统计折线统计(1)________________图能够显示每组中的具体数据.
(2)________________图能够显示部分在总体中的百分比.
(3)________________图能够显示数据的变化趋势.
(4)________________图能够显示数据的分布情况.频数分布直方3.画频数分布直方图的步骤. (1)计算最大值与最小值的差;(2)决定组距与组数;(3)列频
数分布表;(4)画频数分布直方图.
【学有奇招】
数据的整理和描述解题技巧为“找对应,选公式,会估
计”.具体步骤如下:①从统计表和统计图中寻找突破点:对
应的频数、总数、频率;②灵活选用公式:①频数=总数x频
率,②频数之和=总数,③频率之和=1;③会用样本估计总体. 1.下列四种调查:
①调查某班学生的身高情况;②调查某城市的空气质量;
③调查某风景区全年的游客流量;④调查某批汽车的抗撞击能力.其中适合用全面调查方式的是()AA.①B.②C.③D.④ 2.为了解我市七年级学生的身高,从中抽取了 500 名学生,
对其身高进行统计分析,样本是___________________.
500 名学生的身高 3.七年级(1)班与(2)班各选出 20 名学生进行英文打字比赛,
通过对参赛学生每分钟输入的单词个数进行统计,两班成绩的
平均数相同,(1)班成绩的方差为 17.5,(2)班成绩的方差为 15.由此可知________班的成绩更稳定.(2)4.九(1)班参加乒乓球兴趣小组的 15 人身高如下表所示:
他们身高的中位数是__________;众数是________;平均数是________(精确到 0.01).1.701.621.66 求反映数据集中程度的量:平均数、众数、中位数
1.(2013 年广东茂名)商店某天销售了 13 双运动鞋,其尺
码统计如下表:则这 13 双运动鞋尺码的众数和中位数分别是()AA.39 码、39 码
C.40 码、39 码B.39 码、40 码
D.40 码、40 码2.(2013 年福建福州)某校女子排球队队员的年龄分布如下表:则该校女子排球队队员的平均年龄是________岁.14+14×7+15×4)=14(岁).
名师点评:(1)中位数的找法切记先排序,再找中.(2)求加
权平均数找“权”很关键,具体方法为:第 2 题中有两个量,
年龄和人数,问题是求年龄的平均数,人数则为“权”. 解决有关整理和描述数据的频数、频率与统计图问题
例题:(2013 年甘肃兰州)在兰州市开展的“体育、艺术 2
+1”活动中,某校根据实际情况,决定主要开设 A:乒乓球,
B:篮球,C:跑步,D:跳绳,这四种运动项目.为了解学生
喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结
果绘制成如图 7-1-1(1)(2)所示的条形统计图和扇形统计图.请
你结合图中的信息解答下列问题:(1)(2)图7-1-1(1)样本中喜欢 B 项目的人数百分比是______________,其所在扇形统计图中的圆心角的度数是________;(2)把条形统计图补充完整;(3)已知该校有 1000 人,根据样本估计全校喜欢乒乓球的人数是多少?解:(1)1-44%-8%-28%=20%,其所在扇形统计图中的圆心角的度数是:
360°×20%=72°.(2)调查的总人数是:44÷44%=100(人),
则喜欢B 的人数是:100×20%=20(人).
补全条形统计图如图 7-1-2.图 7-1-2(3)全校喜欢乒乓球的人数是1000×44%=440(人).【试题精选】
3.(2013 年河南)从 2013 年 1 月 7 日起,中国中东部大部
分地区持续出现雾霾天气.某市记者为了解雾霾天气的主要原
因,随机调查了该市部分市民,并对调查结果进行整理.绘制了如图 7-1-3 所示的尚不完整的统计图表.图 7-1-3= .请根据图表中提供的信息解答下列问题:
(1)填空:m=________,n=________.扇形统计图中 E 组所占的百分比为________%;4010015 (2)若该市人口约有 100 万人,请你估计其中持 D 组“观
点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查 1 人,则此人持
C 组“观点”的概率是多少?解:(2)100×120
400=30(万人).(3)随机抽查 1 人,则此人持 C 组“观点”的概率是100 1
400 4 名师点评:这类题目通常把各种统计图、统计表结合起来
解决频率、频数问题.“找对应,选公式,会估计”就是解题
技巧. 1.(2012 年广东佛山)吸烟有害健康,被动吸烟也有害健康.
如果要了解人们被动吸烟的情况,那么最合适的调查方式是()A.普查BB.抽样调查
C.在社会上随机调查
D.在学校里随机调查2.(2013 年广东汕头)数学 1,2,5,3,5,3,3 的中位数是()A.1B.2C.3D.5C 3.(2013 年广东茂名)小李和小林练习射箭,射完 10 箭后
两人的成绩如图 7-1-4,通常新手的成绩不太稳定,根据图中的小李信息,估计这两人中的新手是__________.
图 7-1-48.58.50.156 4.(2012 年广东梅州)为参加 2012 年“梅州市实践毕业生
升学体育考试”,小峰同学进行了刻苦训练,在投掷实心球时,
测得 5 次投掷的成绩(单位:m)8,8.5,8.8,8.5,9.2.这组数据的:
①众数是_____;②中位数是____;③方差是______. 5.(2013 年广东深圳)2013 年起,深圳市实施行人闯红灯
违法处罚 , 处罚方式分为四类 : “ 罚 款 20 元 ”“ 罚 款 50
元”“罚款 100 元”“穿绿马甲维护交通”.图 7-1-5 是实施
首日由某片区的执法结果整理数据后绘制的两幅不完整的统计
图,请你根据图中提供的信息,解答下列问题:
(1)实施首日,该片区行人闯红灯违法受处罚一共_____人;
(2)在所有闯红灯违法受处罚的行人中,穿绿马甲维护交通所占的百分比是________%;20065(3)据了解,“罚款 20 元”人数是“罚款 50 元”人数的 2倍,请补全条形统计图;解:补全条形统计图如图 63.图 63(4)根据(3)中的信息,在扇形统计图中,“罚款 20 元”所72在扇形的圆心角等于________度.
图7-1-5 6.(2013 年广东)某校教导处为了解该校七年级同学对排
球、乒乓球、羽毛球、篮球和足球五种球类运动项目的喜爱情
况(每位同学必须且只能选择最喜爱的一项运动项目),进行了
随机抽样调查,并将调查结果统计后绘制成如图 7-1-6 所示的
不完整统计图表.(1)请你补全下列样本人数分布表和条形统计图;(2)若七年级学生总人数为 920 人,请你估计七年级学生喜爱羽毛球运动项目的人数.样本人数分布表图7-1-6解:补全人数分布表如下:补全条形统计图如图64.图 64(2)920×30%=276(人).
七年级学生喜爱羽毛球运动项目的人数为 276 人. 7.(2012 年广东湛江)2013 年3月28日是全国中小学生安
全教育日,某学校为加强学生的安全意识,组织了全校 1500 名
学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整
数,满分为 100 分)进行统计.请根据尚未完成的频率分布表和图7-1-7频数分布直方图(如图 7-1-7),解答下列问题:
频率分布表(1)这次抽取了__________名学生的竞赛成绩进行统计,其中:m=__________,n=________;200700.12 (2)补全频数分布直方图;
(3)若成绩在 70 分以下(含 70 分)的学生为安全意识不强,
有待进一步加强安全教育,则该校
安全意识不强的学生约有多少人?解:(2)如图65.图65(3)1500×(0.2+0.08)=420(人).
同课章节目录
