2014年中考数学总复习提能训练课件第三章 第2讲一次函数
文档属性
| 名称 | 2014年中考数学总复习提能训练课件第三章 第2讲一次函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 405.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:51:19 | ||
图片预览








文档简介
课件30张PPT。第2讲一次函数 1.结合具体情境体会一次函数的意义,根据已知条件确定
一次函数表达式.
2.会画一次函数的图象,根据一次函数的图象和解析式y=
kx+b(k≠0)探索并理解其性质(k>0 或 k<0 时,图象的变化情况).
3.理解正比例函数.
4.能根据一次函数的图象求二元一次方程组的近似解.
5.能用一次函数解决实际问题.考点 1一次函数的图象与性质 1.一次函数的概念.
一般来说,形如__________________的函数叫做一次函数.
特别地,当 b=0 时,称为正比例函数.
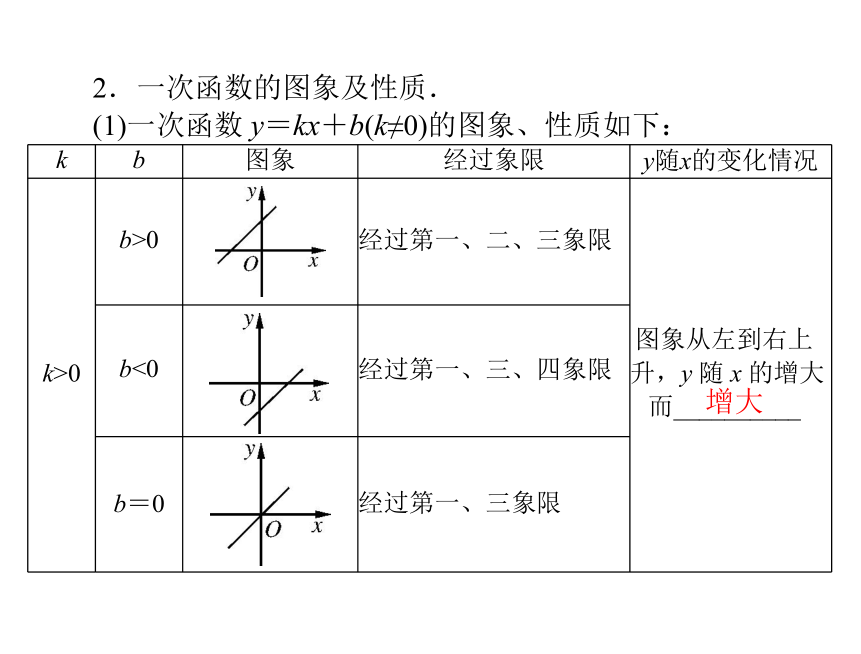
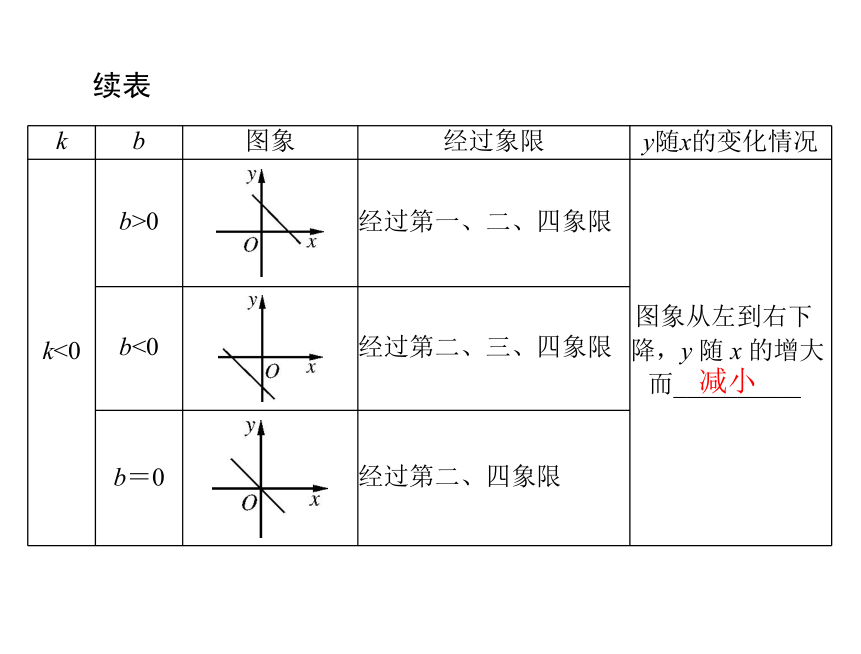
y=kx+b(k≠0)2.一次函数的图象及性质.(1)一次函数 y=kx+b(k≠0)的图象、性质如下:增大续表减小(0,b)(0,0)(2)交点坐标:一次函数 y=kx+b(k≠0)的图象与 x 轴的交点是________,与 y 轴的交点是__________.(3)正比例函数 y=kx(k≠0)的图象恒过________点.
(4)若一次函数 y=kx+b(k≠0)的图象与 x 轴交于点 A,与 y轴交于点 B,则 S△AOB=________.考点 2确定一次函数的表达式1.确定一次函数表达式的条件.1 个2 个2.待定系数法确定一次函数表达式.y=kx+b(k≠0)(1)设:设函数表达式为________________.
(2)代:将已知点的坐标代入函数表达式,解____________.
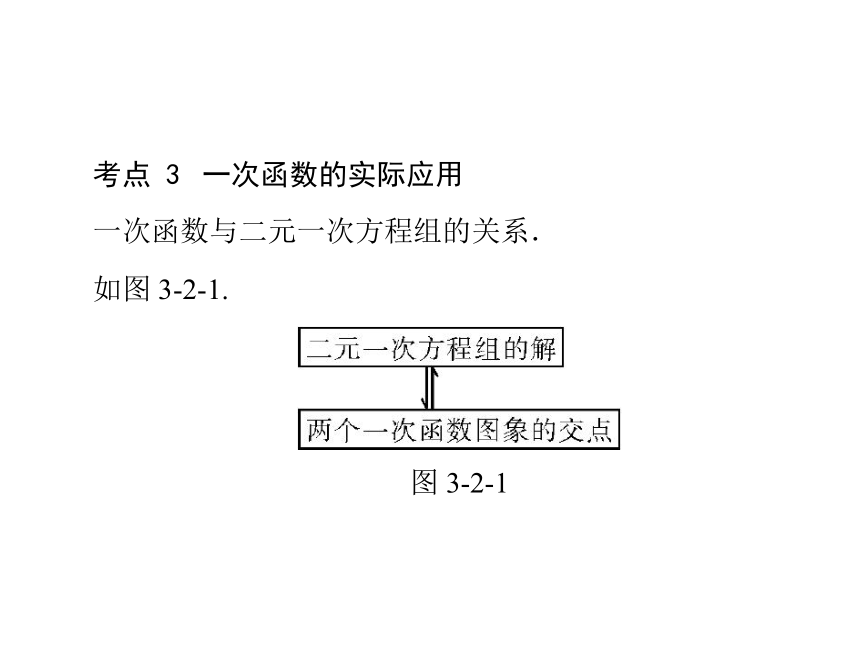
(3)解:求出__________的值,得到函数表达式.方程或方程组k 与 b考点 3一次函数的实际应用一次函数与二元一次方程组的关系.
如图 3-2-1.
图 3-2-1【学有奇招】 一次函数是直线,正比例函数更简单,经过原点一直线;
两个系数 k 与b,作用之大莫小看,k 是斜率定夹角,b 与y 轴
来相见,k 为正来右上斜,x 增减 y 增减;k 为负来左下展,变
化规律正相反;k 的绝对值越大,线离横轴就越远.1.下列点中,不在一次函数 y=-2x+1 的图象上的点是(C )
A.(1,-1 )
C. (2,0)B. (0,1)
D.(-1,3)2.一次函数 y=2x+3 的图象不经过的象限是()DA.第一象限
C.第三象限B.第二象限
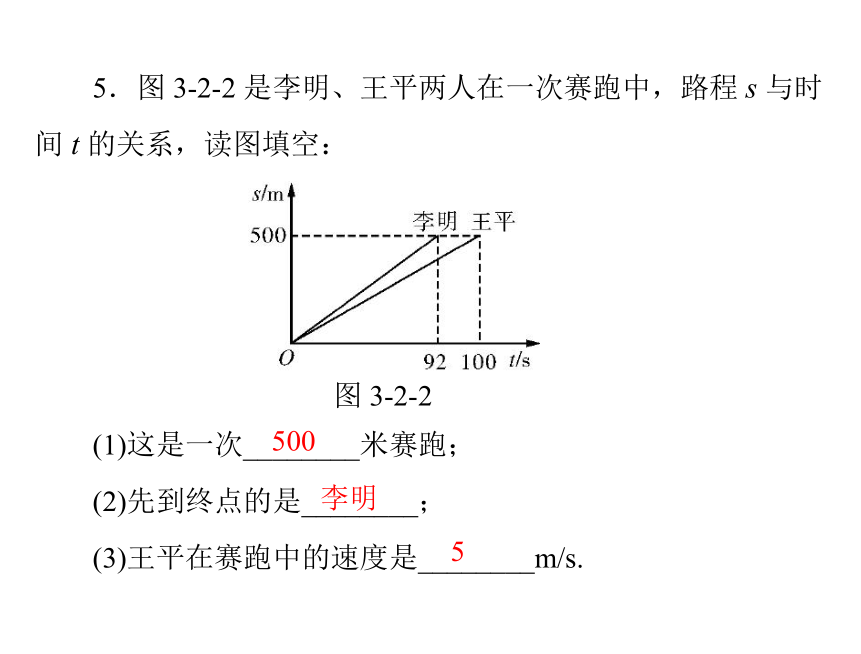
D.第四象限3.写出一个具体的 y 随 x 的增大而减小的一次函数解析式____________.y=-3x+9-24.一次函数 y=kx+3 的图象经过点(-1,5),则 k=_____. 5.图 3-2-2 是李明、王平两人在一次赛跑中,路程 s 与时
间 t 的关系,读图填空:
图 3-2-2(1)这是一次________米赛跑;500李明5(2)先到终点的是________;
(3)王平在赛跑中的速度是________m/s. 一次函数的图象与性质
1.(2013 年山东菏泽)一条直线 y=kx+b,其中 k+b=-5,)kb=6,那么该直线经过(
A.第二、四象限
C.第一、三象限
B.第一、二、三象限
D.第二、三、四象限D2.(2013 年湖南娄底)一次函数 y=kx+b(k≠0)的图象如图3-2-3,当 y>0 时,x 的取值范围是()C图 3-2-3 A.x<0
B.x>0
C.x<2
D.x>2
名师点评:解决这类问题的关键是根据 k,b 的取值确定图
象所在象限,再根据图象来观察 y 随 x 变化的情况. 确定一次函数的表达式
3.(2013 年陕西)根据下表中一次函数的自变量 x 与 y 的对)应值,可得 P 的值为(
A.1
C.3
B.-1
D.-3A
4.(2013 年湖北荆州)体育课上,20 人一组进行足球比赛,
每人射点球 5 次,已知某一组的进球总数为 49 个,进球情况记
录如下表,其中进 2 个球的有 x 人,进 3 个球的有 y 人,若(x,y)恰好是两条直线的交点坐标,则这两条直线的解析式是()C 名师点评:确定一次函数的解析式,一般用待定系数法.
如果 k,b 中知道一个,只需再找一个点的坐标代入即可求;如
果 k,b 都不知道,就必须找两个点的坐标代入得到一个二元一
次方程组来解出 k 和 b 的值.一次函数的实际应用 例题:甲、乙两地相距 300 千米,一辆货车和一辆轿车先
后从甲地出发向乙地,如图 3-2-4,线段 OA 表示货车离甲地的
距离 y(单位:千米)与时间 x(单位:小时)之间的函数关系;折
线 BCD 表示轿车离甲地的距离 y(单位:千米)与 x(单位:小时)
之间的函数关系.请根据图象解答下列问题:图 3-2-4 (1)轿车到达乙地后,货车距乙地多少千米;
(2)求线段 CD 对应的函数解析式;
(3)轿车到达乙地后,马上沿原路以 CD 段速度返回,求货
车从甲地出发后多长时间再与轿车相遇(结果精确到 0.01).解:(1)根据图象信息:货车的速度v货=300
5=60(千米/时). ∵轿车到达乙地的时间为货车出发后4.5 小时,
∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米).
此时,货车距乙地的路程为:300-270=30(千米).
答:轿车到达乙地后,货车距乙地30 千米.【试题精选】 5.(2013 年湖北襄阳)某社区活动中心为鼓励居民加强体育
锻炼,准备购买 10 副某种品牌的羽毛球拍,每副球拍配 x(x≥2)
个羽毛球,供社区居民免费借用.该社区附近 A,B 两家超市
都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均
为 30 元,每个羽毛球的标价为 3 元,目前两家超市同时在做促
销活动.A 超市:所有商品均打九折(按标价的 90%)销售;
B 超市:买一副羽毛球拍送 2 个羽毛球. 设在 A 超市购买羽毛球拍和羽毛球的费用为 yA(单位:元),
在 B 超市购买羽毛球拍和羽毛球的费用为 yB(单位:元).请解
答下列问题:(1)分别写出 yA,yB 与 x 之间的关系式;(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?(3)若每副球拍配 15 个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.解:(1)由题意,得yA=(10×30+3×10x)×0.9=27x+270,
yB=10×30+3(10x-20)=30x+240.(2)当 yA=yB 时,27x+270=30x+240,得 x=10;
当 yA>yB 时,27x+270>30x+240,得 x<10;
当 yA<yB 时,27x+270<30x+240,得 x>10,∴当 2≤x<10 时,到 B 超市购买划算,当 x=10 时,两家超市一样划算,当 x>10 时在 A 超市购买划算.(3)由题意知 x=15>10,∴选择 A 超市,yA=27×15+270=675(元), 先选择 B 超市购买 10 副羽毛球拍,送 20 个羽毛球,然后
在 A 超市购买剩下的羽毛球,所需费用为(10×15-20)×3×0.9
+10×30=651(元),∵651<675,∴最佳方案是先选择 B 超市购买 10 副羽毛球拍,然后在 A超市购买 130 个羽毛球. 名师点评:一次函数的解析式的运用有时会结合分类讨论
的数学思想或方案设计,解答时分段求出函数的解析式是关键.1.(2013年广东广州)一次函数 y=(m+2)x+1,若 y 随 x的增大而增大,则 m 的取值范围是________.m>-2 2.(2013年广东茂名)如图 3-2-5,三个正比例函数的图象
分别对应表达式:①y=ax,②y=bx,③y=cx.将 a,b,c 从小a
图 3-2-5 3.(2013 年广东珠海)已知,函数 y=3x 的图象经过点 A(-1,
y1),点 B(-2,y2),则 y1____y2(填“>”“<”或“=”).
4.(2013 年广东深圳)已知二次函数 y=a(x-1)2-c 的图象)A如图 3-2-6,则一次函数 y=ax+c 的大致图象可能是(
图 3-2-6>5.(2013年广东茂名)如图3-2-7,反比例函数y=—的图象6
x与一次函数 y=kx+b 的图象相交于两点 A(m,3)和 B(-3,n).(1)求一次函数的表达式;(2)观察图象,直接写出使反比例函数值大于一次函数值的自变量 x 的
取值范围.图 3-2-7 6.(2013 年广东湛江)周末,小明骑自行车从家里出发到野
外郊游.从家出发 1 小时后到达南亚所(景点),游玩一段时间
后按原速前往湖光岩.小明离家 1 小时 50 分钟,妈妈驾车沿相
同路线前往湖光岩,图 3-2-8 是他们离家的路程 y(单位:km)与
小明离家时间 x(单位:h)的函数图象.
(1)求小明骑车的速度和在南亚所游
玩的时间;
(2)若妈妈在出发后 25 分钟时,刚
好在湖光岩门口追上小明,求妈妈驾车的速度及 CD 所在直线的函数解析式.图 3-2-8
一次函数表达式.
2.会画一次函数的图象,根据一次函数的图象和解析式y=
kx+b(k≠0)探索并理解其性质(k>0 或 k<0 时,图象的变化情况).
3.理解正比例函数.
4.能根据一次函数的图象求二元一次方程组的近似解.
5.能用一次函数解决实际问题.考点 1一次函数的图象与性质 1.一次函数的概念.
一般来说,形如__________________的函数叫做一次函数.
特别地,当 b=0 时,称为正比例函数.
y=kx+b(k≠0)2.一次函数的图象及性质.(1)一次函数 y=kx+b(k≠0)的图象、性质如下:增大续表减小(0,b)(0,0)(2)交点坐标:一次函数 y=kx+b(k≠0)的图象与 x 轴的交点是________,与 y 轴的交点是__________.(3)正比例函数 y=kx(k≠0)的图象恒过________点.
(4)若一次函数 y=kx+b(k≠0)的图象与 x 轴交于点 A,与 y轴交于点 B,则 S△AOB=________.考点 2确定一次函数的表达式1.确定一次函数表达式的条件.1 个2 个2.待定系数法确定一次函数表达式.y=kx+b(k≠0)(1)设:设函数表达式为________________.
(2)代:将已知点的坐标代入函数表达式,解____________.
(3)解:求出__________的值,得到函数表达式.方程或方程组k 与 b考点 3一次函数的实际应用一次函数与二元一次方程组的关系.
如图 3-2-1.
图 3-2-1【学有奇招】 一次函数是直线,正比例函数更简单,经过原点一直线;
两个系数 k 与b,作用之大莫小看,k 是斜率定夹角,b 与y 轴
来相见,k 为正来右上斜,x 增减 y 增减;k 为负来左下展,变
化规律正相反;k 的绝对值越大,线离横轴就越远.1.下列点中,不在一次函数 y=-2x+1 的图象上的点是(C )
A.(1,-1 )
C. (2,0)B. (0,1)
D.(-1,3)2.一次函数 y=2x+3 的图象不经过的象限是()DA.第一象限
C.第三象限B.第二象限
D.第四象限3.写出一个具体的 y 随 x 的增大而减小的一次函数解析式____________.y=-3x+9-24.一次函数 y=kx+3 的图象经过点(-1,5),则 k=_____. 5.图 3-2-2 是李明、王平两人在一次赛跑中,路程 s 与时
间 t 的关系,读图填空:
图 3-2-2(1)这是一次________米赛跑;500李明5(2)先到终点的是________;
(3)王平在赛跑中的速度是________m/s. 一次函数的图象与性质
1.(2013 年山东菏泽)一条直线 y=kx+b,其中 k+b=-5,)kb=6,那么该直线经过(
A.第二、四象限
C.第一、三象限
B.第一、二、三象限
D.第二、三、四象限D2.(2013 年湖南娄底)一次函数 y=kx+b(k≠0)的图象如图3-2-3,当 y>0 时,x 的取值范围是()C图 3-2-3 A.x<0
B.x>0
C.x<2
D.x>2
名师点评:解决这类问题的关键是根据 k,b 的取值确定图
象所在象限,再根据图象来观察 y 随 x 变化的情况. 确定一次函数的表达式
3.(2013 年陕西)根据下表中一次函数的自变量 x 与 y 的对)应值,可得 P 的值为(
A.1
C.3
B.-1
D.-3A
4.(2013 年湖北荆州)体育课上,20 人一组进行足球比赛,
每人射点球 5 次,已知某一组的进球总数为 49 个,进球情况记
录如下表,其中进 2 个球的有 x 人,进 3 个球的有 y 人,若(x,y)恰好是两条直线的交点坐标,则这两条直线的解析式是()C 名师点评:确定一次函数的解析式,一般用待定系数法.
如果 k,b 中知道一个,只需再找一个点的坐标代入即可求;如
果 k,b 都不知道,就必须找两个点的坐标代入得到一个二元一
次方程组来解出 k 和 b 的值.一次函数的实际应用 例题:甲、乙两地相距 300 千米,一辆货车和一辆轿车先
后从甲地出发向乙地,如图 3-2-4,线段 OA 表示货车离甲地的
距离 y(单位:千米)与时间 x(单位:小时)之间的函数关系;折
线 BCD 表示轿车离甲地的距离 y(单位:千米)与 x(单位:小时)
之间的函数关系.请根据图象解答下列问题:图 3-2-4 (1)轿车到达乙地后,货车距乙地多少千米;
(2)求线段 CD 对应的函数解析式;
(3)轿车到达乙地后,马上沿原路以 CD 段速度返回,求货
车从甲地出发后多长时间再与轿车相遇(结果精确到 0.01).解:(1)根据图象信息:货车的速度v货=300
5=60(千米/时). ∵轿车到达乙地的时间为货车出发后4.5 小时,
∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米).
此时,货车距乙地的路程为:300-270=30(千米).
答:轿车到达乙地后,货车距乙地30 千米.【试题精选】 5.(2013 年湖北襄阳)某社区活动中心为鼓励居民加强体育
锻炼,准备购买 10 副某种品牌的羽毛球拍,每副球拍配 x(x≥2)
个羽毛球,供社区居民免费借用.该社区附近 A,B 两家超市
都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均
为 30 元,每个羽毛球的标价为 3 元,目前两家超市同时在做促
销活动.A 超市:所有商品均打九折(按标价的 90%)销售;
B 超市:买一副羽毛球拍送 2 个羽毛球. 设在 A 超市购买羽毛球拍和羽毛球的费用为 yA(单位:元),
在 B 超市购买羽毛球拍和羽毛球的费用为 yB(单位:元).请解
答下列问题:(1)分别写出 yA,yB 与 x 之间的关系式;(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?(3)若每副球拍配 15 个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.解:(1)由题意,得yA=(10×30+3×10x)×0.9=27x+270,
yB=10×30+3(10x-20)=30x+240.(2)当 yA=yB 时,27x+270=30x+240,得 x=10;
当 yA>yB 时,27x+270>30x+240,得 x<10;
当 yA<yB 时,27x+270<30x+240,得 x>10,∴当 2≤x<10 时,到 B 超市购买划算,当 x=10 时,两家超市一样划算,当 x>10 时在 A 超市购买划算.(3)由题意知 x=15>10,∴选择 A 超市,yA=27×15+270=675(元), 先选择 B 超市购买 10 副羽毛球拍,送 20 个羽毛球,然后
在 A 超市购买剩下的羽毛球,所需费用为(10×15-20)×3×0.9
+10×30=651(元),∵651<675,∴最佳方案是先选择 B 超市购买 10 副羽毛球拍,然后在 A超市购买 130 个羽毛球. 名师点评:一次函数的解析式的运用有时会结合分类讨论
的数学思想或方案设计,解答时分段求出函数的解析式是关键.1.(2013年广东广州)一次函数 y=(m+2)x+1,若 y 随 x的增大而增大,则 m 的取值范围是________.m>-2 2.(2013年广东茂名)如图 3-2-5,三个正比例函数的图象
分别对应表达式:①y=ax,②y=bx,③y=cx.将 a,b,c 从小a
图 3-2-5 3.(2013 年广东珠海)已知,函数 y=3x 的图象经过点 A(-1,
y1),点 B(-2,y2),则 y1____y2(填“>”“<”或“=”).
4.(2013 年广东深圳)已知二次函数 y=a(x-1)2-c 的图象)A如图 3-2-6,则一次函数 y=ax+c 的大致图象可能是(
图 3-2-6>5.(2013年广东茂名)如图3-2-7,反比例函数y=—的图象6
x与一次函数 y=kx+b 的图象相交于两点 A(m,3)和 B(-3,n).(1)求一次函数的表达式;(2)观察图象,直接写出使反比例函数值大于一次函数值的自变量 x 的
取值范围.图 3-2-7 6.(2013 年广东湛江)周末,小明骑自行车从家里出发到野
外郊游.从家出发 1 小时后到达南亚所(景点),游玩一段时间
后按原速前往湖光岩.小明离家 1 小时 50 分钟,妈妈驾车沿相
同路线前往湖光岩,图 3-2-8 是他们离家的路程 y(单位:km)与
小明离家时间 x(单位:h)的函数图象.
(1)求小明骑车的速度和在南亚所游
玩的时间;
(2)若妈妈在出发后 25 分钟时,刚
好在湖光岩门口追上小明,求妈妈驾车的速度及 CD 所在直线的函数解析式.图 3-2-8
同课章节目录
