2014年中考数学总复习提能训练课件第三章 第4讲二次函数
文档属性
| 名称 | 2014年中考数学总复习提能训练课件第三章 第4讲二次函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 676.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:52:31 | ||
图片预览










文档简介
课件41张PPT。第4讲二次函数 1.通过对实际问题情境的分析确定二次函数的表达式,并
体会二次函数的意义.
2.会用描点法画出二次函数的图象,能从图象上认识二次
函数的性质.
3.会根据公式确定图象的顶点、开口方向和对称轴(公式
不要求记忆和推导),并能解决简单的实际问题.
4.会利用二次函数的图象求一元二次方程的近似解.考点 1二次函数1.二次函数的概念.y=ax2+bx+c 形如________________(a,b,c 是常数,a≠0)的函数,叫
做二次函数.表达式法数表法2.二次函数的三种表示方法.
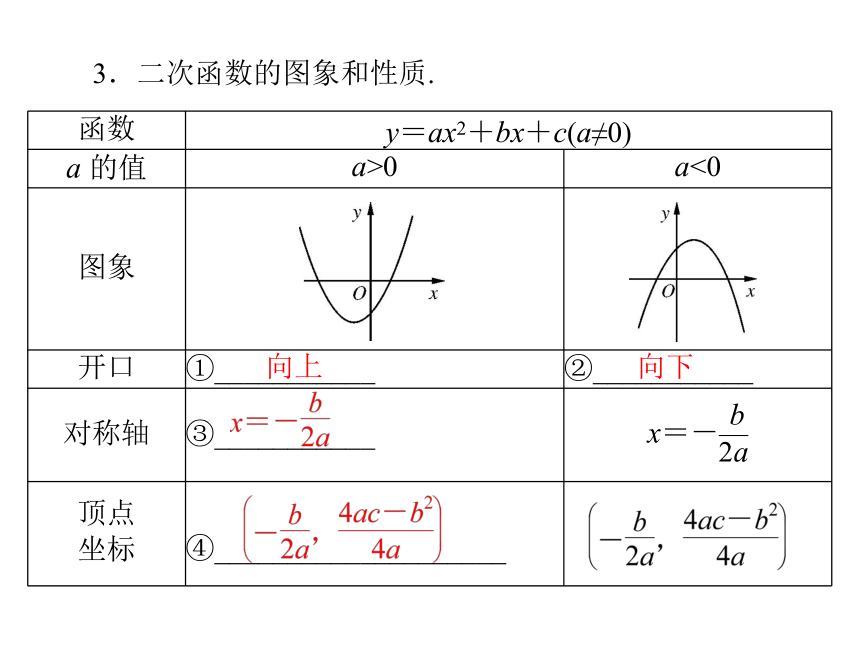
_________、图象法和_________.3.二次函数的图象和性质.向上向下小续表考点2系数 a,b,c 和Δ的符号 1.系数 a,b,c 的几何意义.
(1)开口方向:__________的符号决定抛物线的开口方向.
(2)当 a,b 同号,对称轴在 y 轴________边;当 a,b 异号,
对称轴在 y 轴________边.
(3)______的符号确定抛物线与 y 轴的交点在正半轴或负半
轴或原点.a左右c2.二次函数与一元二次方程中Δ的关系.两个有两个相等的实数根无交点考点3二次函数的解析式1.待定系数法求二次函数的解析式.y=a(x-h)2+k(a≠0) y=ax2+bx+c(a≠0)
y=a(x-x1)(x-x2)(a≠0)的图象2.二次函数的平移与解析式的关系.
y=ax2 的图象y =a(x -h)2向②______(k>0)或向下(k<0)平移|k|个单位y =a(x -h)2+k 的图象.上左考点4二次函数的综合运用 1.从实际问题中抽象出二次函数,并能利用二次函数的最
值问题解决实际问题中的最值问题.
2.二次函数综合几何图形,要充分抓住几何图形的特点并
结合二次函数图象的特点才能有效解决问题.二次函数综合动
点问题,要弄清楚在动的过程中,什么变了,什么没变.动中
求静才能有效解决问题.【学有奇招】1.通过配方,可以确定顶点坐标,对称轴,进而可以找出抛物线的平移规律,所以掌握配方法非常重要. 2.二次函数的图象性质及单调性的规律:确定抛物线的对
称轴及开口方向.当抛物线开口向下的时候离对称轴越近,对
应的函数值就越大;当抛物线开口向上的时候离对称轴越近,
对应的函数值就越小.1.以 P(-2,-6)为顶点的二次函数是()CA.y=5(x+2)2+6
C.y=5(x+2)2-6B.y=5(x-2)2+6
D.y=5(x-2)2-62.把抛物线 y=-2x2 向上平移 1 个单位,得到的抛物线是()CA.y=-2(x+1)2
C.y=-2x2+1 B.y=-2(x-1)2
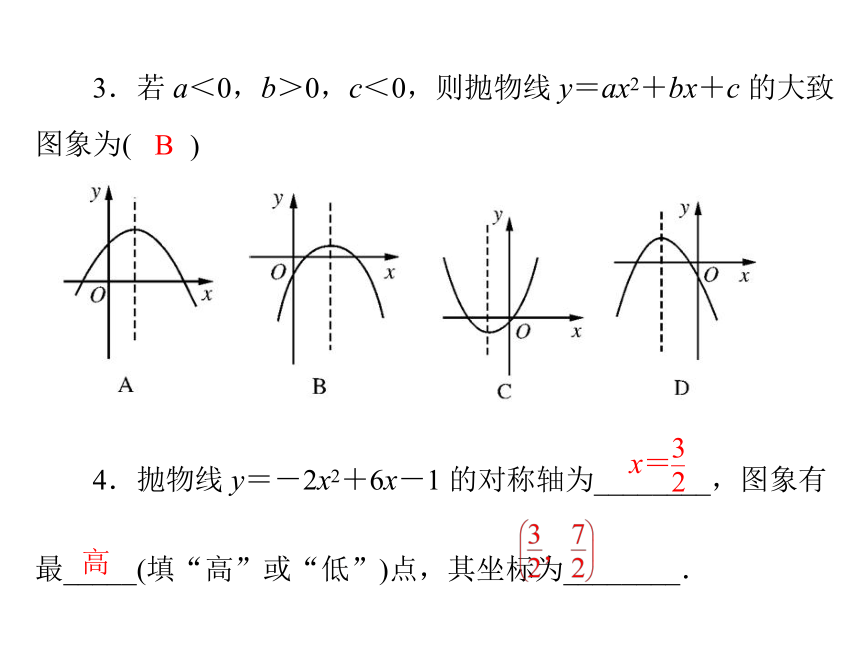
D.y=-2x2-13.若 a<0,b>0,c<0,则抛物线 y=ax2+bx+c 的大致图象为()B4.抛物线 y=-2x2+6x-1 的对称轴为________,图象有最_____(填“高”或“低”)点,其坐标为________.高
=________;当 x________时,y 随 x 的增大而减小.5<5 二次函数的图象和性质D⑤a=—b.你认为其中正确信息的个数有( 2.(2013 年湖北鄂州)小轩从如图 3-4-1 所示的二次函数 y
=ax2+bx+c(a≠0)的图象中,观察得出了下面信息:①ab>0;
②a+b+c<0;③b+2c>0;④a-2b+4c>0;)D 3
2
A.2 个B.3 个C.4 个D.5 个图 3-4-1 名师点评:本类题考查的是二次函数的系数符号,先看a,
c,Δ的符号,再结合对称轴推出b 的符号;同时含有a,b,c
的代数式,尽量找到特殊点;此外,还可以把图中的已知点代
入帮助解题.2确定二次函数的关系式 例题:(2012年江苏泰州)如图3-4-2,在平面直角坐标系xOy
中,边长为 2 的正方形 OABC 的顶点 A,C 分别在 x 轴,y 轴的3正半轴上,二次函数 y=-—x2+bx+c 的图象经过 B,C 两点. (1)求该二次函数的解析式;
(2)结合函数的图象探索:
当 y>0 时,x 的取值范围.图 3-4-2【试题精选】
3.(2013 年贵州遵义节选)如图3-4-3,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为
,且与 y 轴交于点 C(0,2),与 x 轴交于 A,B 两点(点 A 在点 B 的左边).求抛物线的解析式
及 A,B 两点的坐标.
图 3-4-3 名师点评:求二次函数的解析式,要根据问题中所给的条
件,合理地选择二次函数的三种表达式(一般式、顶点式、两点
式)进行假设,对快速解决问题有很大的帮助.二次函数的综合运用 例题:(2012 年江苏连云港)如图 3-4-4(1),抛物线 y=-x2
+bx+c 与 x 轴交于 A,B 两点,与 y 轴交于点 C,点 O 为坐标
原点,点 D 为抛物线的顶点,点 E 在抛物线上,点 F 在 x 轴上,
四边形 OCEF 为矩形,且 OF=2,EF=3.(1)求抛物线所对应的函数解析式;
(2)求△ABD 的面积;(3)将△AOC绕点C逆时针旋转90°,点A的对应点为点G,问点 G 是否在该抛物线上?请说明理由.(1)(2) 图3-4-4
解:(1)∵四边形OCEF为矩形,OF=2,EF=3,
∴点C 的坐标为(0,3),点E 的坐标为(2,3).
把C(0,3),E(2,3)分别代入y=-x2+bx+c,得c=3,
-4+2b+c=3,解得b=2,
c=3.∴抛物线所对应的函数解析式为y=-x2+2x+3.∴△ABD的面积=—×4×4=8.(2)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线的顶点坐标为D(1,4).
∴△ABD 中AB 边的高为 4.令 y=0,得-x2+2x+3=0,解得x1=-1,x2=3.
∴AB=3-(-1)=4.1
2(3)如图3-4-4(2),△AOC 绕点C逆时针旋转90°,CO落在CE 所在的直线上,由(1)(2)可知 OA=1,OC=3,∵点 A 的对应点 G 的坐标为(3,2).∵当 x=3 时,y=-32+2×3+3=0≠2,
∴点 G 不在该抛物线上.【试题精选】
4.(2013 年湖北天门)2013 年 5 月 26 日,中国羽毛球队蝉
联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛
球的某次运动路线可以看作是一条抛物线(如图 3-4-5).若不考
虑外力因素,羽毛球行进高度 y(单位:米)与水平距离 x(单位:为________米.图 3-4-55与直线 y=—x+2 交5.如图 3-4-6,抛物线y=-x2+bx+c1
2于 C,D 两点,其中点 C 在 y 轴上,点 D 的坐标为
点 P 是 y 轴右侧的抛物线上一动点,过点
P 作 PE⊥x 轴于点 E,交 CD 于点 F.
(1)求抛物线的解析式;
(2)若点 P 的横坐标为 m,当 m
为何值时,以 O,C,P,F 为顶点的四边形是平行四边形?请说明理由.图 3-4-6
1.(2013 年广东湛江)抛物线 y=x2+1 的最小值是______.
2.(2013 年广东深圳)已知二次函数 y=a(x-1)2-c 的图象)A如图 3-4-7,则一次函数 y=ax+c 的大致图象可能是(
1图 3-4-7 3.(2012 年广东珠海)如图 3-4-8,二次函数 y=(x-2)2+m
的图象与 y 轴交于点 C,点 B 是点 C 关于该二次函数图象的对
称轴对称的点.已知一次函数 y=kx+b 的图象经过该二次函数
图象上的点 A(1,0)及点 B. (1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足 kx+b≥
(x-2)2+m 的 x 的取值范围.图 3-4-8(2)∵点 A,B 坐标分别为(1,0),(4,3),∴当 kx+b≥(x-2)2+m 时,直线 y=x-1 的图象在抛物线y=(x-2)2-1 的图象上方或相交,此时 1≤x≤4.4.(2013 年广东佛山)如图 3-4-9(1),已知抛物线 y=ax2+bx+c 经过点 A(0,3),B(3,0),C(4,3) .(1)求抛物线的函数表达式;(2)求抛物线的顶点坐标和对称轴; (3)把抛物线向上平移,使得顶点落在 x 轴上,直接写出两
条抛物线、对称轴和 y 轴围成的图形的面积 S[图 3-4-9(2)中阴影
部分].(1) (2)
图3-4-9 解:(1) ∵抛物线 y =ax2 +bx +c 经过点 A(0,3) ,B(3,0) ,
C(4,3), c=3,
∴ 9a+3b+c=0,
16a+4b+c=3, a=1,
解得 b=-4,
c=3.∴抛物线的函数表达式为 y=x2-4x+3.
(2)∵y=x2-4x+3=(x-2)2-1,
∴抛物线的顶点坐标为(2,-1),对称轴为直线 x=2.(3)如图 10,∵抛物线的顶点坐标为(2,-1),
∴PP′=1.阴影部分的面积等于平行四边形 A′APP′的面积,
平行四边形 A′APP′的面积=1×2=2,
∴阴影部分的面积为 2.图 10 5.(2013年广东广州)已知抛物线y1=ax2+bx+c(a≠0,a≠c)
过点 A(1,0),顶点为 B,且抛物线不经过第三象限.
(1)使用 a,c 表示 b;
(2)判断点 B 所在象限,并说明理由;
(3)若直线 y2=2x+m 经过点 B,且于该抛物线交于另一点,求当 x≥1 时,y1 的取值范围.∵x1=1,x2=—,a≠c,解:(1)抛物线过点 A(1,0),则有 a+b+c=0,即 b=-a-c.
(2)点 B 在第四象限.理由如下:c
a∴抛物线与 x 轴有两个交点.
∵抛物线不经过第三象限,
∴a>0,且顶点在第四象限.
∴点 B 在第四象限.又∵a+c=8,则有 c(8-c+2)=24.
解得 c=4 或 c=6.
当 c=4 时,a=8-c=4,又 a≠c,故舍去;
当 c=6 时,a=8-c=2.
画图易知(如图 11),
点 C 在点 A 的右侧,
∴当 x≥1 时,y1≥4ac-b2
4a=-2.图 116.(2012 年广东茂名)如图 3-4-10,抛物线y=ax2+—x+c
经过原点 O 和 A(4,2),与 x 轴交于点 C,点 M,N 同时从原点
O 出发,点 M 以 2 个单位/秒的速度沿 y 轴正方向运动,点 N
以 1 个单位/秒的速度沿 x 轴正方向运动,当其中一个点停止运
动时,另一点也随之停止.
(1)求抛物线的解析式和点 C 的坐标;
(2)在点 M,N 运动过程中,
①若线段 MN 与 OA 交于点 G,试判断 MN 与 OA 的位置关系,并说明理由;图 3-4-103
2 ②若线段 MN 与抛物线相交于点 P,探索:是否存在某一
时刻 t,使得以 O,P,A,C 为顶点的四边形是等腰梯形?若存
在,请求出 t 的值;若不存在,请说明理由.== .(2)①MN⊥OA.理由如下:
过点 A 作 AB⊥x 轴于点 B,则 OB=4,AB=2.由已知,可得OM OB 2
ON AB 1∴Rt△MON∽Rt∠OBA.
∴∠NMO=∠AOB,∠MNO=∠OAB.
又∵∠AOB+∠OAB=90°,
∴∠AOB+∠MNO=90°.
∴∠OGN=90°,∴MN⊥OA. ②存在.理由如下:
设点 P 的坐标为(x,y),依题意可知,当点 P 是点 A 关于
抛物线对称轴的对称点时,四边形 APOC 为等腰梯形.
则点 P 坐标为(2,2),及 M(0,2t),N(t,0).
设直线 MN 的解析式为 y=kx+2t,将点 N,P 的坐标代入,得kt+2t=0,
2k+2t=2,解得t1=0,
k1=1,(不合题意舍去)或t2=3,
k2=-2.∴当 t=3 秒时,四边形 OPAC 是等腰梯形.
体会二次函数的意义.
2.会用描点法画出二次函数的图象,能从图象上认识二次
函数的性质.
3.会根据公式确定图象的顶点、开口方向和对称轴(公式
不要求记忆和推导),并能解决简单的实际问题.
4.会利用二次函数的图象求一元二次方程的近似解.考点 1二次函数1.二次函数的概念.y=ax2+bx+c 形如________________(a,b,c 是常数,a≠0)的函数,叫
做二次函数.表达式法数表法2.二次函数的三种表示方法.
_________、图象法和_________.3.二次函数的图象和性质.向上向下小续表考点2系数 a,b,c 和Δ的符号 1.系数 a,b,c 的几何意义.
(1)开口方向:__________的符号决定抛物线的开口方向.
(2)当 a,b 同号,对称轴在 y 轴________边;当 a,b 异号,
对称轴在 y 轴________边.
(3)______的符号确定抛物线与 y 轴的交点在正半轴或负半
轴或原点.a左右c2.二次函数与一元二次方程中Δ的关系.两个有两个相等的实数根无交点考点3二次函数的解析式1.待定系数法求二次函数的解析式.y=a(x-h)2+k(a≠0) y=ax2+bx+c(a≠0)
y=a(x-x1)(x-x2)(a≠0)的图象2.二次函数的平移与解析式的关系.
y=ax2 的图象y =a(x -h)2向②______(k>0)或向下(k<0)平移|k|个单位y =a(x -h)2+k 的图象.上左考点4二次函数的综合运用 1.从实际问题中抽象出二次函数,并能利用二次函数的最
值问题解决实际问题中的最值问题.
2.二次函数综合几何图形,要充分抓住几何图形的特点并
结合二次函数图象的特点才能有效解决问题.二次函数综合动
点问题,要弄清楚在动的过程中,什么变了,什么没变.动中
求静才能有效解决问题.【学有奇招】1.通过配方,可以确定顶点坐标,对称轴,进而可以找出抛物线的平移规律,所以掌握配方法非常重要. 2.二次函数的图象性质及单调性的规律:确定抛物线的对
称轴及开口方向.当抛物线开口向下的时候离对称轴越近,对
应的函数值就越大;当抛物线开口向上的时候离对称轴越近,
对应的函数值就越小.1.以 P(-2,-6)为顶点的二次函数是()CA.y=5(x+2)2+6
C.y=5(x+2)2-6B.y=5(x-2)2+6
D.y=5(x-2)2-62.把抛物线 y=-2x2 向上平移 1 个单位,得到的抛物线是()CA.y=-2(x+1)2
C.y=-2x2+1 B.y=-2(x-1)2
D.y=-2x2-13.若 a<0,b>0,c<0,则抛物线 y=ax2+bx+c 的大致图象为()B4.抛物线 y=-2x2+6x-1 的对称轴为________,图象有最_____(填“高”或“低”)点,其坐标为________.高
=________;当 x________时,y 随 x 的增大而减小.5<5 二次函数的图象和性质D⑤a=—b.你认为其中正确信息的个数有( 2.(2013 年湖北鄂州)小轩从如图 3-4-1 所示的二次函数 y
=ax2+bx+c(a≠0)的图象中,观察得出了下面信息:①ab>0;
②a+b+c<0;③b+2c>0;④a-2b+4c>0;)D 3
2
A.2 个B.3 个C.4 个D.5 个图 3-4-1 名师点评:本类题考查的是二次函数的系数符号,先看a,
c,Δ的符号,再结合对称轴推出b 的符号;同时含有a,b,c
的代数式,尽量找到特殊点;此外,还可以把图中的已知点代
入帮助解题.2确定二次函数的关系式 例题:(2012年江苏泰州)如图3-4-2,在平面直角坐标系xOy
中,边长为 2 的正方形 OABC 的顶点 A,C 分别在 x 轴,y 轴的3正半轴上,二次函数 y=-—x2+bx+c 的图象经过 B,C 两点. (1)求该二次函数的解析式;
(2)结合函数的图象探索:
当 y>0 时,x 的取值范围.图 3-4-2【试题精选】
3.(2013 年贵州遵义节选)如图3-4-3,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为
,且与 y 轴交于点 C(0,2),与 x 轴交于 A,B 两点(点 A 在点 B 的左边).求抛物线的解析式
及 A,B 两点的坐标.
图 3-4-3 名师点评:求二次函数的解析式,要根据问题中所给的条
件,合理地选择二次函数的三种表达式(一般式、顶点式、两点
式)进行假设,对快速解决问题有很大的帮助.二次函数的综合运用 例题:(2012 年江苏连云港)如图 3-4-4(1),抛物线 y=-x2
+bx+c 与 x 轴交于 A,B 两点,与 y 轴交于点 C,点 O 为坐标
原点,点 D 为抛物线的顶点,点 E 在抛物线上,点 F 在 x 轴上,
四边形 OCEF 为矩形,且 OF=2,EF=3.(1)求抛物线所对应的函数解析式;
(2)求△ABD 的面积;(3)将△AOC绕点C逆时针旋转90°,点A的对应点为点G,问点 G 是否在该抛物线上?请说明理由.(1)(2) 图3-4-4
解:(1)∵四边形OCEF为矩形,OF=2,EF=3,
∴点C 的坐标为(0,3),点E 的坐标为(2,3).
把C(0,3),E(2,3)分别代入y=-x2+bx+c,得c=3,
-4+2b+c=3,解得b=2,
c=3.∴抛物线所对应的函数解析式为y=-x2+2x+3.∴△ABD的面积=—×4×4=8.(2)∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线的顶点坐标为D(1,4).
∴△ABD 中AB 边的高为 4.令 y=0,得-x2+2x+3=0,解得x1=-1,x2=3.
∴AB=3-(-1)=4.1
2(3)如图3-4-4(2),△AOC 绕点C逆时针旋转90°,CO落在CE 所在的直线上,由(1)(2)可知 OA=1,OC=3,∵点 A 的对应点 G 的坐标为(3,2).∵当 x=3 时,y=-32+2×3+3=0≠2,
∴点 G 不在该抛物线上.【试题精选】
4.(2013 年湖北天门)2013 年 5 月 26 日,中国羽毛球队蝉
联苏迪曼杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛
球的某次运动路线可以看作是一条抛物线(如图 3-4-5).若不考
虑外力因素,羽毛球行进高度 y(单位:米)与水平距离 x(单位:为________米.图 3-4-55与直线 y=—x+2 交5.如图 3-4-6,抛物线y=-x2+bx+c1
2于 C,D 两点,其中点 C 在 y 轴上,点 D 的坐标为
点 P 是 y 轴右侧的抛物线上一动点,过点
P 作 PE⊥x 轴于点 E,交 CD 于点 F.
(1)求抛物线的解析式;
(2)若点 P 的横坐标为 m,当 m
为何值时,以 O,C,P,F 为顶点的四边形是平行四边形?请说明理由.图 3-4-6
1.(2013 年广东湛江)抛物线 y=x2+1 的最小值是______.
2.(2013 年广东深圳)已知二次函数 y=a(x-1)2-c 的图象)A如图 3-4-7,则一次函数 y=ax+c 的大致图象可能是(
1图 3-4-7 3.(2012 年广东珠海)如图 3-4-8,二次函数 y=(x-2)2+m
的图象与 y 轴交于点 C,点 B 是点 C 关于该二次函数图象的对
称轴对称的点.已知一次函数 y=kx+b 的图象经过该二次函数
图象上的点 A(1,0)及点 B. (1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足 kx+b≥
(x-2)2+m 的 x 的取值范围.图 3-4-8(2)∵点 A,B 坐标分别为(1,0),(4,3),∴当 kx+b≥(x-2)2+m 时,直线 y=x-1 的图象在抛物线y=(x-2)2-1 的图象上方或相交,此时 1≤x≤4.4.(2013 年广东佛山)如图 3-4-9(1),已知抛物线 y=ax2+bx+c 经过点 A(0,3),B(3,0),C(4,3) .(1)求抛物线的函数表达式;(2)求抛物线的顶点坐标和对称轴; (3)把抛物线向上平移,使得顶点落在 x 轴上,直接写出两
条抛物线、对称轴和 y 轴围成的图形的面积 S[图 3-4-9(2)中阴影
部分].(1) (2)
图3-4-9 解:(1) ∵抛物线 y =ax2 +bx +c 经过点 A(0,3) ,B(3,0) ,
C(4,3), c=3,
∴ 9a+3b+c=0,
16a+4b+c=3, a=1,
解得 b=-4,
c=3.∴抛物线的函数表达式为 y=x2-4x+3.
(2)∵y=x2-4x+3=(x-2)2-1,
∴抛物线的顶点坐标为(2,-1),对称轴为直线 x=2.(3)如图 10,∵抛物线的顶点坐标为(2,-1),
∴PP′=1.阴影部分的面积等于平行四边形 A′APP′的面积,
平行四边形 A′APP′的面积=1×2=2,
∴阴影部分的面积为 2.图 10 5.(2013年广东广州)已知抛物线y1=ax2+bx+c(a≠0,a≠c)
过点 A(1,0),顶点为 B,且抛物线不经过第三象限.
(1)使用 a,c 表示 b;
(2)判断点 B 所在象限,并说明理由;
(3)若直线 y2=2x+m 经过点 B,且于该抛物线交于另一点,求当 x≥1 时,y1 的取值范围.∵x1=1,x2=—,a≠c,解:(1)抛物线过点 A(1,0),则有 a+b+c=0,即 b=-a-c.
(2)点 B 在第四象限.理由如下:c
a∴抛物线与 x 轴有两个交点.
∵抛物线不经过第三象限,
∴a>0,且顶点在第四象限.
∴点 B 在第四象限.又∵a+c=8,则有 c(8-c+2)=24.
解得 c=4 或 c=6.
当 c=4 时,a=8-c=4,又 a≠c,故舍去;
当 c=6 时,a=8-c=2.
画图易知(如图 11),
点 C 在点 A 的右侧,
∴当 x≥1 时,y1≥4ac-b2
4a=-2.图 116.(2012 年广东茂名)如图 3-4-10,抛物线y=ax2+—x+c
经过原点 O 和 A(4,2),与 x 轴交于点 C,点 M,N 同时从原点
O 出发,点 M 以 2 个单位/秒的速度沿 y 轴正方向运动,点 N
以 1 个单位/秒的速度沿 x 轴正方向运动,当其中一个点停止运
动时,另一点也随之停止.
(1)求抛物线的解析式和点 C 的坐标;
(2)在点 M,N 运动过程中,
①若线段 MN 与 OA 交于点 G,试判断 MN 与 OA 的位置关系,并说明理由;图 3-4-103
2 ②若线段 MN 与抛物线相交于点 P,探索:是否存在某一
时刻 t,使得以 O,P,A,C 为顶点的四边形是等腰梯形?若存
在,请求出 t 的值;若不存在,请说明理由.== .(2)①MN⊥OA.理由如下:
过点 A 作 AB⊥x 轴于点 B,则 OB=4,AB=2.由已知,可得OM OB 2
ON AB 1∴Rt△MON∽Rt∠OBA.
∴∠NMO=∠AOB,∠MNO=∠OAB.
又∵∠AOB+∠OAB=90°,
∴∠AOB+∠MNO=90°.
∴∠OGN=90°,∴MN⊥OA. ②存在.理由如下:
设点 P 的坐标为(x,y),依题意可知,当点 P 是点 A 关于
抛物线对称轴的对称点时,四边形 APOC 为等腰梯形.
则点 P 坐标为(2,2),及 M(0,2t),N(t,0).
设直线 MN 的解析式为 y=kx+2t,将点 N,P 的坐标代入,得kt+2t=0,
2k+2t=2,解得t1=0,
k1=1,(不合题意舍去)或t2=3,
k2=-2.∴当 t=3 秒时,四边形 OPAC 是等腰梯形.
同课章节目录
