2014年中考数学总复习提能训练课件第四章 第3讲 第1课时
文档属性
| 名称 | 2014年中考数学总复习提能训练课件第四章 第3讲 第1课时 |

|
|
| 格式 | zip | ||
| 文件大小 | 296.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:55:17 | ||
图片预览







文档简介
课件24张PPT。 第3讲
第 1 课时 四边形与多边形
多边形与平行四边形1.了解多边形的内角和与外角和公式,了解正多边形的概念.2.掌握平行四边形的概念和性质,了解四边形的不稳定性.
3.掌握平行四边形的有关性质和四边形是平行四边形的条件.4.了解平行四边形的重心及物理意义(如一根均匀木棒或一块均匀的矩形木板的重心).5.知道任意一个三角形、四边形或正六边形可以镶嵌平面,并能运用这几种图形进行简单的镶嵌设计.考点 1多边形(n-2)·180°360°1.多边形的性质.n-3n-2 n 边形内角和公式为__________,外角和为_________;
从 n 边形的一个顶点可以引__________条对角线,并且这
些对角线把多边形分成了_________个三角形;
n 边形对角线条数为____________;正 n 边形的每个内角为______________.2.多边形的镶嵌.360正四边形 (1)当围绕一点拼在一起的几个多边形的内角和为_______
度时,可以镶嵌.
(2) 同一种正多边形可以镶嵌的正多边形是正三角形、
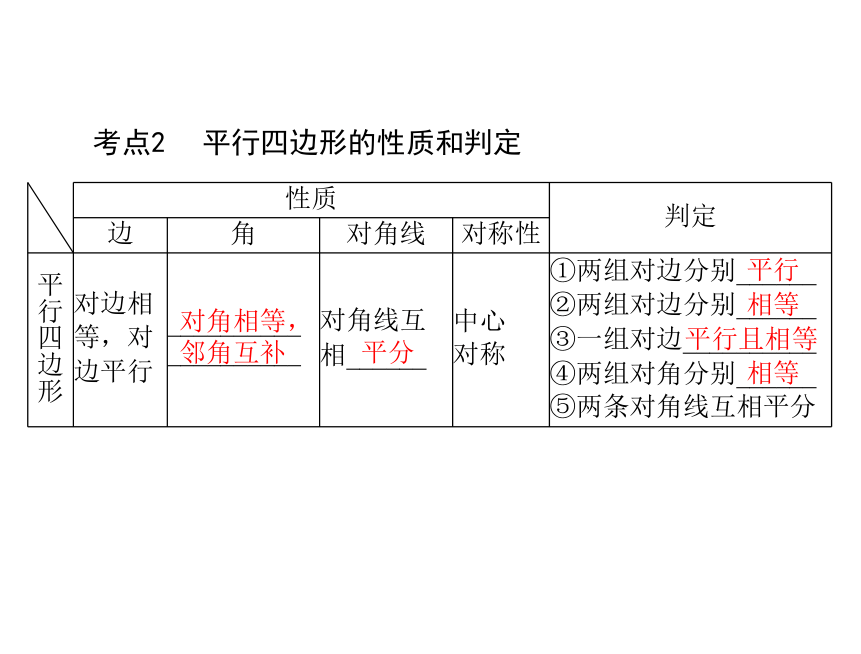
____________ 和正六边形.考点2平行四边形的性质和判定对角相等,
邻角互补平分平行相等平行且相等相等 由平行四边形的性质可得到重要的结论:①平行四边形相
邻两边之和等于周长的一半;②平行四边形被对角线分成的四
个小三角形中,相邻两个三角形的周长之差等于相邻两边之差;
③平行四边形是中心对称图形,对角线的交点为对称中心;
④SABCD=边长×相应高;⑤由平行四边形中“旋转 180°可重合”
的两个三角形可观察出有关线段、角、周长、面积、形状等之
间的关系.【学有奇招】 1.平行四边形的判定:要证平行四边形,两个条件才能行,
一证对边都相等,或证对边都平行,一组对边也可以,必须相
等且平行;对角线,是个宝,互相平分跑不了;对角相等也不
孬,两组对角凑热闹. 2.平行四边形的性质都是通过连接对角线把四边形问题转
化成三角形问题来处理的,应用平行四边形的性质解决某些问
题,如计算角的度数,线段的长度,证明两线平行、线段相等
以及角相等.1.平行四边形一边长是 6 厘米,周长是 28 厘米,则这条)边的邻边长为(
A.22 厘米
C.11 厘米
B.16 厘米
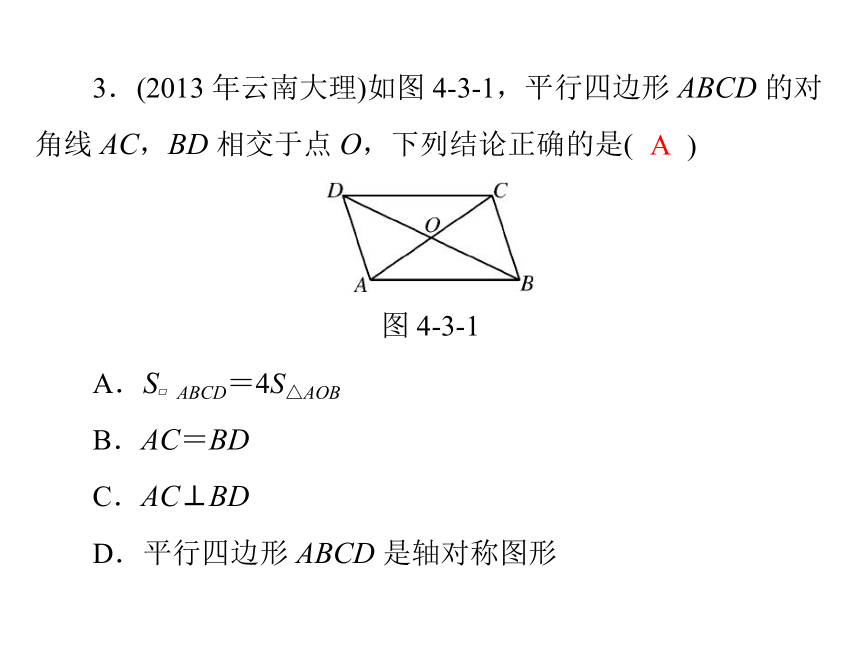
D.8 厘米2.若一个多边形的内角和等于900°,则这个多边形的边数是()BA.6B.7C.8D.9D3.(2013 年云南大理)如图 4-3-1,平行四边形 ABCD 的对)角线 AC,BD 相交于点 O,下列结论正确的是(
图 4-3-1A.S?ABCD=4S△AOBAB.AC=BD
C.AC⊥BD
D.平行四边形 ABCD 是轴对称图形4.在正三角形、正四边形、正五边形和正六边形中不能单独密铺的是______________.正五边形 5.如图 4-3-2,点 E 是?ABCD 的边 CD 的中点,AD,BE
的延长线相交于点 F,DF =3 ,DE =2 ,则?ABCD 的周长是______________.
图 4-3-214 与多边形有关的计算
1.(2013 年四川眉山)一个正多边形的每个外角都是 36°,这个正多边形的边数是()BA.9B.10C.11D.122.(2013 年山东烟台)一个多边形截去一个角后, 形成另一个多边形的内角和为 720°,那么原多边形的边数为()DA.5
C.5 或 7B.5 或 6
D.5 或 6 或 7 名师点评:有关多边形的角、对角线计算问题,常设未知
数 x(度数、边数、点数等)表示多边形内角和、外角的度数,借
助图形性质、定理、公式等把相关问题转化为方程问题(方程思
想)来求解.平行四边形的性质与判定 例题:(2013 年青海)如图 4-3-3,已知?ABCD,过 A 作 AM
⊥BC 于 M,交 BD 于 E,过 C 作 CN⊥AD 于 N,交 BD 于 F,
连接 AF,CE.求证:四边形 AECF 为平行四边形.图4-3-3思路分析:可先证△ABE≌△CDF,再证AE∥CF,AE=CF.证明:在?ABCD 中,AD ∥ BC,AB=CD,∠ABC=∠ADC,
∴∠ABD=∠CDB.又∵AM⊥BC,CN⊥AD,∴∠BAM=∠DCN.
∴△ABE≌△CDF.∴AE=CF,∠AEB=∠CFD.
∴∠AEF=∠CFE.∴AE∥CF.
∴四边形 AECF 为平行四边形.点,延长BC到点E,使CE=—BC,连接DE,CF.【试题精选】3.(2013 年北京)如图 4-3-4,在?ABCD 中,F 是 AD 的中1
2(1)求证:四边形 CEDF 是平行四边形;(2)若 AB=4,AD=6,∠B=60°,求 DE 的长.图 4-3-4 名师点评:要证一个四边形是平行四边形,关键是分析与
判断容易得到平行四边形的一组条件为基础,再设法寻找与其搭配的另一组判定条件:即一组对边相等证另一组对边相等
证这组对边平行或一组对边平行证另一组对边平行
证这组对边相等或图中有对角线—— 证对角线互相平分.考点3平面图形的密铺与镶嵌4.(2013 年内蒙古呼和浩特)只用下列图形中的一种,能够)进行平面镶嵌的是(
A. 正十边形
C. 正六边形
B. 正八边形
D. 正五边形C 5.(2013 年山东威海)如图 4-3-5(1),将四边形纸片 ABCD
沿两组对边中点连线剪切为四部分,将这四部分密铺可得到如
图 4-3-5(2)所示的平行四边形.若要使密铺后的平行四边形为矩
形,则四边形 ABCD 需要满足的条件是__________.图 4-3-5名师点评:判断多边形是否镶嵌, 关键是看围绕一点拼在一起的多边形的内角是否恰好组成一个周角.AC=BD1.(2013年广东湛江)已知一个多边形的内角和是540°,则)这个多边形是(
A.四边形
C.六边形
B.五边形
D.七边形2.(2013 年广东梅州)一个多边形的内角和小于它的外角A和,则这个多边形的边数是(
A.3
C.5 )
B.4
D.6B 3.(2013 年广东汕头)一个六边形的内角和是_______.
4.(2013 年广东)如图 4-3-6,将一张直角三角形纸片 ABC
沿中位线 DE 剪开后,在平面上将△BDE 绕着 CB 的中点 D 逆
时针旋转 180°,点 E 到了点 E′位置,则四边形ACE′E 的形状是____________.720°
图 4-3-6平行四边形 5.(2012 年广东湛江)如图 4-3-7,在平行四边形 ABCD 中,
E,F 分别在边 AD,BC 上,且 AE=CF.
求证:(1)△ABE≌△CDF;(2)四边形 BFDE 是平行四边形.图 4-3-7证明:(1)∵四边形 ABCD 是平行四边形,
∴AB=CD,∠A=∠C.
又∵AE=CF,∴△ABE≌△CDF.
(2)∵四边形 ABCD 是平行四边形,∴AD=BC,AD∥BC.
又∵AE=CF,∴AD-AE=BC-CF.∴DE=BF.
又∵DE∥BF,∴四边形 BFDE 是平行四边形. 6.(2013 年广东茂名)如图 4-3-8,在平行四边形 ABCD 中,
E 是 AB 的中点,连接 DE 并延长,交 CB 的延长线于 F.(1)求证:△ADE≌△BFE;(2)若 DF 平分∠ADC,连接 CE.试判断 CE 与 DF 的位置关系,并说明理由.图 4-3-8(1)证明:∵四边形 ABCD 是平行四边形,
∴AD∥BC.∴∠ADE=∠F,∠A=∠EBF.
∵点 E 是 AB 边的中点,∴AE=BE.
∴△ADE≌△BFE.(2)解:CE⊥DF.理由如下:连接 CE,
∵DF 平分∠ADC,∴∠ADE=∠CDF.∵∠ADE=∠F,∴∠CDF=∠F.∴CD=CF.
又∵△ADE≌△BFE,
∴DE=FE,∴CE⊥DF.
第 1 课时 四边形与多边形
多边形与平行四边形1.了解多边形的内角和与外角和公式,了解正多边形的概念.2.掌握平行四边形的概念和性质,了解四边形的不稳定性.
3.掌握平行四边形的有关性质和四边形是平行四边形的条件.4.了解平行四边形的重心及物理意义(如一根均匀木棒或一块均匀的矩形木板的重心).5.知道任意一个三角形、四边形或正六边形可以镶嵌平面,并能运用这几种图形进行简单的镶嵌设计.考点 1多边形(n-2)·180°360°1.多边形的性质.n-3n-2 n 边形内角和公式为__________,外角和为_________;
从 n 边形的一个顶点可以引__________条对角线,并且这
些对角线把多边形分成了_________个三角形;
n 边形对角线条数为____________;正 n 边形的每个内角为______________.2.多边形的镶嵌.360正四边形 (1)当围绕一点拼在一起的几个多边形的内角和为_______
度时,可以镶嵌.
(2) 同一种正多边形可以镶嵌的正多边形是正三角形、
____________ 和正六边形.考点2平行四边形的性质和判定对角相等,
邻角互补平分平行相等平行且相等相等 由平行四边形的性质可得到重要的结论:①平行四边形相
邻两边之和等于周长的一半;②平行四边形被对角线分成的四
个小三角形中,相邻两个三角形的周长之差等于相邻两边之差;
③平行四边形是中心对称图形,对角线的交点为对称中心;
④SABCD=边长×相应高;⑤由平行四边形中“旋转 180°可重合”
的两个三角形可观察出有关线段、角、周长、面积、形状等之
间的关系.【学有奇招】 1.平行四边形的判定:要证平行四边形,两个条件才能行,
一证对边都相等,或证对边都平行,一组对边也可以,必须相
等且平行;对角线,是个宝,互相平分跑不了;对角相等也不
孬,两组对角凑热闹. 2.平行四边形的性质都是通过连接对角线把四边形问题转
化成三角形问题来处理的,应用平行四边形的性质解决某些问
题,如计算角的度数,线段的长度,证明两线平行、线段相等
以及角相等.1.平行四边形一边长是 6 厘米,周长是 28 厘米,则这条)边的邻边长为(
A.22 厘米
C.11 厘米
B.16 厘米
D.8 厘米2.若一个多边形的内角和等于900°,则这个多边形的边数是()BA.6B.7C.8D.9D3.(2013 年云南大理)如图 4-3-1,平行四边形 ABCD 的对)角线 AC,BD 相交于点 O,下列结论正确的是(
图 4-3-1A.S?ABCD=4S△AOBAB.AC=BD
C.AC⊥BD
D.平行四边形 ABCD 是轴对称图形4.在正三角形、正四边形、正五边形和正六边形中不能单独密铺的是______________.正五边形 5.如图 4-3-2,点 E 是?ABCD 的边 CD 的中点,AD,BE
的延长线相交于点 F,DF =3 ,DE =2 ,则?ABCD 的周长是______________.
图 4-3-214 与多边形有关的计算
1.(2013 年四川眉山)一个正多边形的每个外角都是 36°,这个正多边形的边数是()BA.9B.10C.11D.122.(2013 年山东烟台)一个多边形截去一个角后, 形成另一个多边形的内角和为 720°,那么原多边形的边数为()DA.5
C.5 或 7B.5 或 6
D.5 或 6 或 7 名师点评:有关多边形的角、对角线计算问题,常设未知
数 x(度数、边数、点数等)表示多边形内角和、外角的度数,借
助图形性质、定理、公式等把相关问题转化为方程问题(方程思
想)来求解.平行四边形的性质与判定 例题:(2013 年青海)如图 4-3-3,已知?ABCD,过 A 作 AM
⊥BC 于 M,交 BD 于 E,过 C 作 CN⊥AD 于 N,交 BD 于 F,
连接 AF,CE.求证:四边形 AECF 为平行四边形.图4-3-3思路分析:可先证△ABE≌△CDF,再证AE∥CF,AE=CF.证明:在?ABCD 中,AD ∥ BC,AB=CD,∠ABC=∠ADC,
∴∠ABD=∠CDB.又∵AM⊥BC,CN⊥AD,∴∠BAM=∠DCN.
∴△ABE≌△CDF.∴AE=CF,∠AEB=∠CFD.
∴∠AEF=∠CFE.∴AE∥CF.
∴四边形 AECF 为平行四边形.点,延长BC到点E,使CE=—BC,连接DE,CF.【试题精选】3.(2013 年北京)如图 4-3-4,在?ABCD 中,F 是 AD 的中1
2(1)求证:四边形 CEDF 是平行四边形;(2)若 AB=4,AD=6,∠B=60°,求 DE 的长.图 4-3-4 名师点评:要证一个四边形是平行四边形,关键是分析与
判断容易得到平行四边形的一组条件为基础,再设法寻找与其搭配的另一组判定条件:即一组对边相等证另一组对边相等
证这组对边平行或一组对边平行证另一组对边平行
证这组对边相等或图中有对角线—— 证对角线互相平分.考点3平面图形的密铺与镶嵌4.(2013 年内蒙古呼和浩特)只用下列图形中的一种,能够)进行平面镶嵌的是(
A. 正十边形
C. 正六边形
B. 正八边形
D. 正五边形C 5.(2013 年山东威海)如图 4-3-5(1),将四边形纸片 ABCD
沿两组对边中点连线剪切为四部分,将这四部分密铺可得到如
图 4-3-5(2)所示的平行四边形.若要使密铺后的平行四边形为矩
形,则四边形 ABCD 需要满足的条件是__________.图 4-3-5名师点评:判断多边形是否镶嵌, 关键是看围绕一点拼在一起的多边形的内角是否恰好组成一个周角.AC=BD1.(2013年广东湛江)已知一个多边形的内角和是540°,则)这个多边形是(
A.四边形
C.六边形
B.五边形
D.七边形2.(2013 年广东梅州)一个多边形的内角和小于它的外角A和,则这个多边形的边数是(
A.3
C.5 )
B.4
D.6B 3.(2013 年广东汕头)一个六边形的内角和是_______.
4.(2013 年广东)如图 4-3-6,将一张直角三角形纸片 ABC
沿中位线 DE 剪开后,在平面上将△BDE 绕着 CB 的中点 D 逆
时针旋转 180°,点 E 到了点 E′位置,则四边形ACE′E 的形状是____________.720°
图 4-3-6平行四边形 5.(2012 年广东湛江)如图 4-3-7,在平行四边形 ABCD 中,
E,F 分别在边 AD,BC 上,且 AE=CF.
求证:(1)△ABE≌△CDF;(2)四边形 BFDE 是平行四边形.图 4-3-7证明:(1)∵四边形 ABCD 是平行四边形,
∴AB=CD,∠A=∠C.
又∵AE=CF,∴△ABE≌△CDF.
(2)∵四边形 ABCD 是平行四边形,∴AD=BC,AD∥BC.
又∵AE=CF,∴AD-AE=BC-CF.∴DE=BF.
又∵DE∥BF,∴四边形 BFDE 是平行四边形. 6.(2013 年广东茂名)如图 4-3-8,在平行四边形 ABCD 中,
E 是 AB 的中点,连接 DE 并延长,交 CB 的延长线于 F.(1)求证:△ADE≌△BFE;(2)若 DF 平分∠ADC,连接 CE.试判断 CE 与 DF 的位置关系,并说明理由.图 4-3-8(1)证明:∵四边形 ABCD 是平行四边形,
∴AD∥BC.∴∠ADE=∠F,∠A=∠EBF.
∵点 E 是 AB 边的中点,∴AE=BE.
∴△ADE≌△BFE.(2)解:CE⊥DF.理由如下:连接 CE,
∵DF 平分∠ADC,∴∠ADE=∠CDF.∵∠ADE=∠F,∴∠CDF=∠F.∴CD=CF.
又∵△ADE≌△BFE,
∴DE=FE,∴CE⊥DF.
同课章节目录
