2014年中考数学总复习提能训练课件第四章 第3讲 第2课时
文档属性
| 名称 | 2014年中考数学总复习提能训练课件第四章 第3讲 第2课时 |

|
|
| 格式 | zip | ||
| 文件大小 | 533.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 00:00:00 | ||
图片预览






文档简介
课件33张PPT。第 2 课时特殊的平行四边形 1.掌握矩形、菱形、正方形的概念和性质,了解它们之间
的关系.
2.掌握四边形是矩形、菱形、正方形的条件.
3.了解矩形的重心及物理意义(如一根均匀木棒、一块均
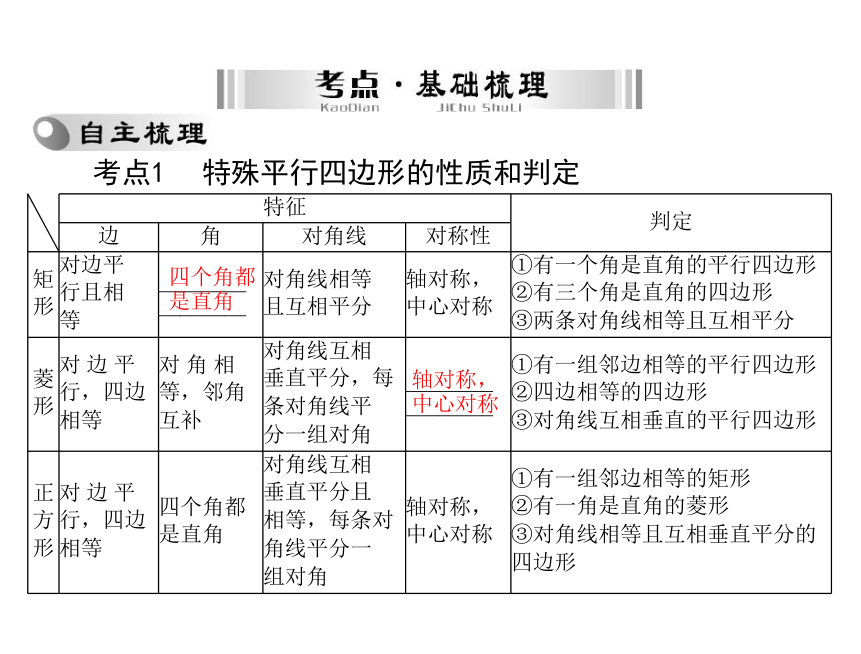
匀的矩形木板的重心).四个角都
是直角轴对称,
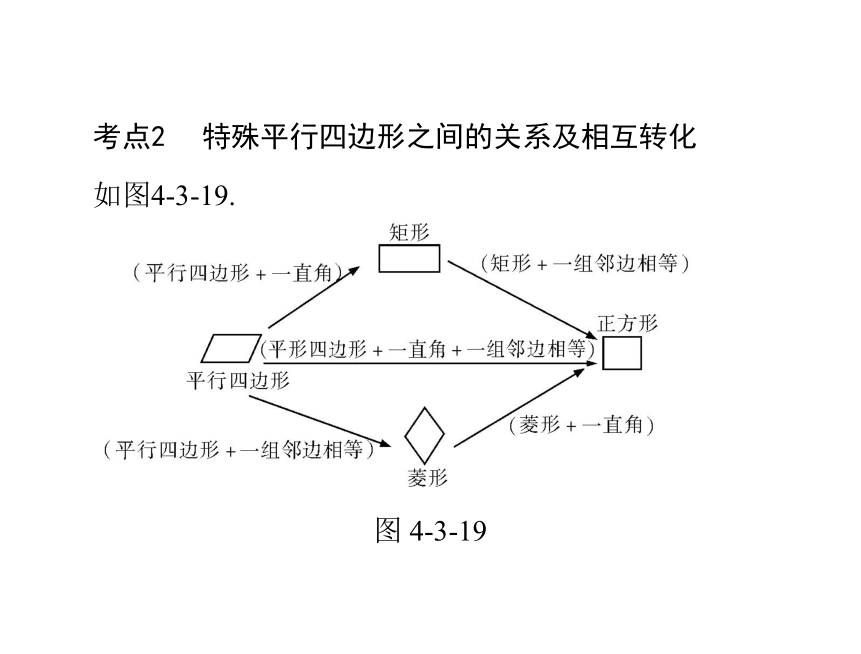
中心对称考点1特殊平行四边形的性质和判定考点2特殊平行四边形之间的关系及相互转化如图4-3-19.
图 4-3-19考点 3四边形的有关计算1.矩形面积=长×宽.
2.平行四边形面积=底×高.
1
2
1
23.菱形面积=底×高=—×两条对角线的积.
4.正方形面积=边长×边长=—×两条对角线的积.【学有奇招】1.口诀.(1)矩形的判定:任意一个四边形,三个直角成矩形;对角线等互平分,四边形它是矩形.已知平行四边形,一个直角叫矩形;两对角线若相等,理所当然为矩形.(2)菱形的判定:任意一个四边形,四边相等成菱形;四边形的对角线,垂直平分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.2.一般证明正方形的步骤是先证四边形是矩形或菱形.)1.矩形、菱形、正方形都具有的性质是(
A.对角线相等BB.对角线互相平分
C.对角线平分一组对角
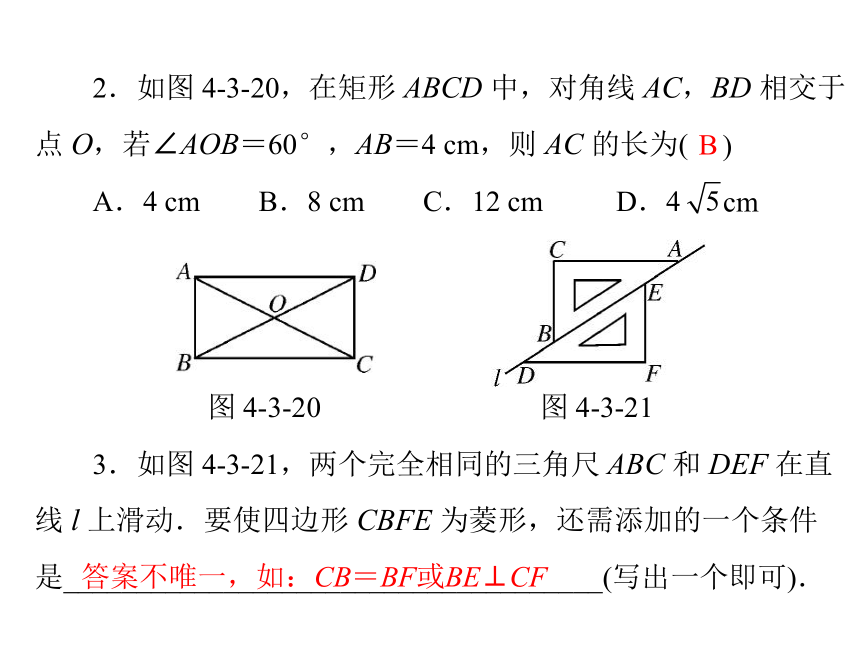
D.对角线互相垂直2.如图 4-3-20,在矩形 ABCD 中,对角线 AC,BD 相交于点 O,若∠AOB=60°,AB=4 cm,则 AC 的长为()BA.4 cmB.8 cmC.12 cmD.4cm 图 4-3-20图 4-3-21 3.如图 4-3-21,两个完全相同的三角尺 ABC 和 DEF 在直
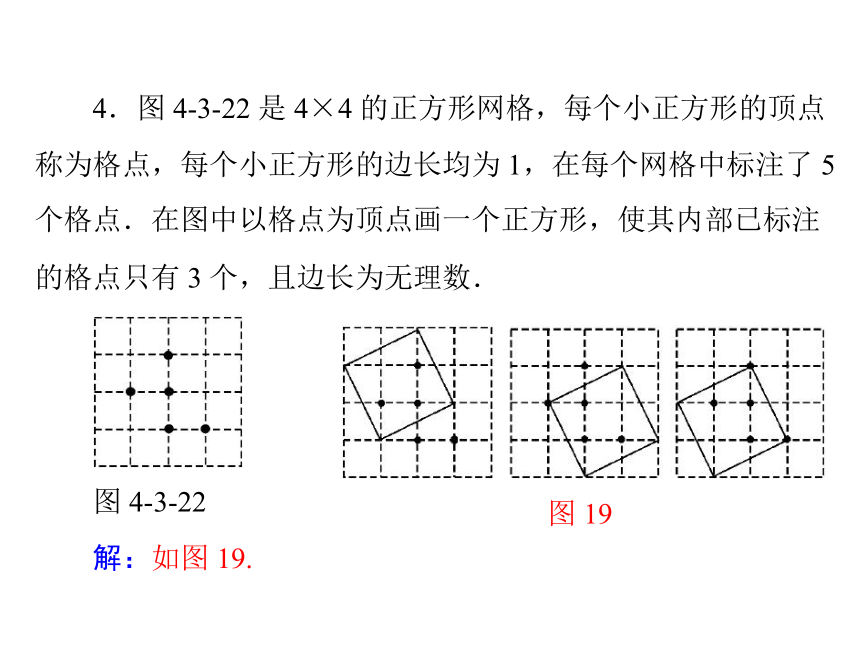
线 l 上滑动.要使四边形 CBFE 为菱形,还需添加的一个条件是_____________________________________(写出一个即可).答案不唯一,如:CB=BF或BE⊥CF 4.图 4-3-22 是 4×4 的正方形网格,每个小正方形的顶点
称为格点,每个小正方形的边长均为 1,在每个网格中标注了 5
个格点.在图中以格点为顶点画一个正方形,使其内部已标注
的格点只有 3 个,且边长为无理数.图 19图 4-3-22
解:如图 19. 菱形的性质与判定
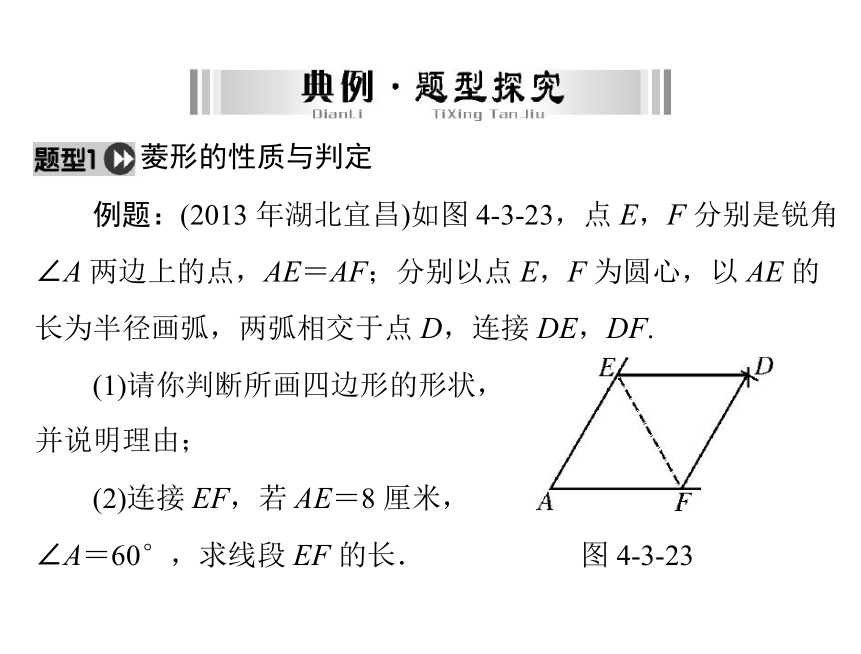
例题:(2013 年湖北宜昌)如图 4-3-23,点 E,F 分别是锐角
∠A 两边上的点,AE=AF;分别以点 E,F 为圆心,以 AE 的
长为半径画弧,两弧相交于点 D,连接 DE,DF.
(1)请你判断所画四边形的形状,
并说明理由;
(2)连接 EF,若 AE=8 厘米,∠A=60°,求线段 EF 的长.图 4-3-23解:(1) 四边形AEDF 为菱形.理由:由尺规作图的过程,可知 AE=AF=ED=DF.
(2)连接EF.∵AE=AF,∠A=60°,
∴△EAF 为等边三角形.
∴EF=AE=8 厘米.【试题精选】
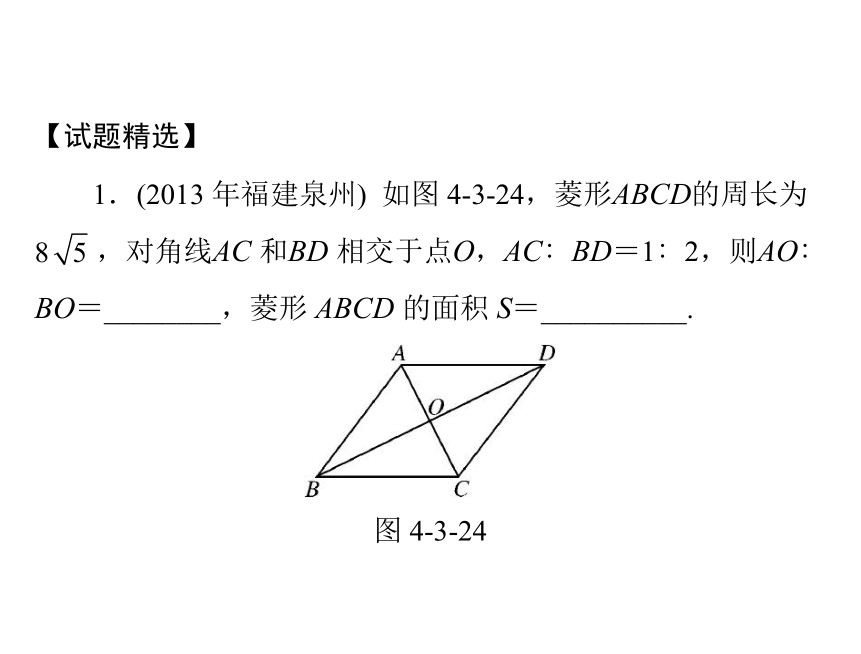
1.(2013 年福建泉州) 如图 4-3-24,菱形ABCD的周长为8,对角线AC 和BD 相交于点O,AC∶BD=1∶2,则AO∶ BO=________,菱形 ABCD 的面积 S=__________.
图 4-3-24答案:1∶216 2.(2013 年四川遂宁)如图4-3-25,已知四边形 ABCD 是平行
四边形,DE⊥AB,DF⊥BC,垂足分别是 E,F,并且 DE=DF.
求证:(1)△ADE≌△CDF;(2)四边形 ABCD 是菱形.图 4-3-25证明:(1)∵DE⊥AB,DF⊥BC,
∴∠AED=∠CFD=90°.
∵四边形 ABCD 是平行四边形,∴∠A=∠C.
∠AED=∠CFD,
在△AED 和△CFD 中, ∠A=∠C,
DE=DF,
∴△AED≌△CFD(AAS).(2)∵△AED≌△CFD,∴AD=CD.
∵四边形 ABCD 是平行四边形,
∴四边形 ABCD 是菱形. 名师点评:菱形的性质可以用于证明线段相等、角相等、
直线平行、垂直等,常与三角形全等、勾股定理、方程相结合
进行相关问题的计算与证明. 矩形的性质与判定
3.(2013 年四川资阳)在矩形 ABCD 中,对角线 ACBD 相交于点 O,若∠AOB=60°,AC=10,则 AB=_____.5 4.(2013 年云南大理)如图 4-3-26,已知在△ABC 中,AB
=AC=5,BC=6,AD 是 BC 边上的中线,四边形 ADBE 是平
行四边形.
(1)求证:四边形 ADBE 是矩形;
(2)求矩形 ADBE 的面积.
图 4-3-26(1)证明:∵AB=AC,AD 是 BC 边上的中线,
∴AD⊥BC,∴∠ADB=90°.∵四边形 ADBE 是平行四边形,
∴平行四边形 ADBE 是矩形. 名师点评:矩形的四个角为直角,常将矩形转化为直角三
角形, 矩形的对角线将矩形分成四个等腰(全等)三角形,这些
及矩形性质是证明线段、角相等以及线段平行、垂直的重要依
据. 正方形的性质与判定
例题:(2013 年湖北鄂州)如图 4-3-27,正方形ABCD的边
长为 4,E,F 分别为 DC,BC 的中点.
(1)求证:△ADE≌△ABF;(2)求△AEF 的面积.图 4-3-27【试题精选】 5.(2013 年福建厦门)如图 4-3-28,在正方形 ABCD 中,点
G 是边 BC 上的任意一点,DE⊥AG,垂足为 E,延长 DE 交 AB
于点 F.在线段 AG 上取点 H,使得 AG=DE+HG,连接 BH.求
证:∠ABH=∠CDE.图 4-3-28证明:∵四边形 ABCD 是正方形,∴∠FAD =90°.
∵DE⊥AG,∴∠AED=90°.∴∠FAG +∠EAD=∠ADF+∠EAD.
∴∠FAG =∠ADF.∵AG=DE+HG=AH+HG,∴DE=AH.
又 AD=AB,∴ △ADE≌△BAH.∴∠ABH=∠DAE.∴∠AHB=∠AED=90°.∵∠ADC=90°,∴∠BAH+∠ABH=∠ADF+∠CDE.
∴∠ABH=∠CDE. 名师点评:与正方形有关的计算及推理题常与三角形的全
等、勾股定理、方程、三角函数相联系,有关正方形的判定方
法较多,一般在矩形、菱形的基础上,从边、角、对角线三个
方向进一步分析、判断与证明.1.(2013 年广东茂名)如图 4-3-29,矩形 ABCD 的两条对角线相交于点O,∠AOD=60°,AD=2,则AC 的长是()A.2B.4C.2D.4B图 4-3-29 2.(2013 年广东深圳)如图 4-3-30,有一张一个角为 30°、
最小边长为 2 的直角三角形纸片,沿图中所示的中位线剪开后,)将两部分拼成一个四边形,所得四边形的周长是(
图 4-3-30D 3.(2013 年广东珠海)如图 4-3-31,正方形 ABCD 的边长为
1 , 顺次连接正方形ABCD四边的中点得到第一个正方形
A1B1C1D1,又顺次连接正方形 A1B1C1D1 四边中点得到第二个正
方形 A2B2C2D2,…,以此类推,则第六个正方形 A6B6C6D6 周长
是________.图 4-3-31答案:1
2 4.(2013 年广东广州)如图 4-3-32,四边形 ABCD 是菱形,
对角线 AC 与 BD 相交于 O,AB=5,AO=4,求 BD 的长.图 4-3-32解:∵四边形 ABCD 是菱形,
∴AC⊥BD,且 BO=DO.在 Rt△AOB 中,∵AB=5,AO=4,
由勾股定理,得 BO=3.∴BD=6. 5.(2013 年广东梅州)如图4-3-33,在四边形 ABFC 中,
∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,
且CF=AE.(1)求证:四边形 BECF 是菱形;(2)若四边形 BECF 为正方形,求∠A 的度数.图 4-3-33(1)证明:∵BC 的垂直平分线 EF 交 BC 于点 D,
∴BF=CF,BE=CE.∴E 为 AB 中点,即 BE=AE.
∵CF=AE,∴CF=BE.
∴CF=BF=BE=CE.
∴四边形 BECF 是菱形.(2)解:如图20,∵四边形BECF为正方形,∴∠BEC=90°.又 AE=CE,∴∠A=45°.图 206.(2011 年广东肇庆)如图4-3-34,在正方形ABCD 中,E为对角线 AC 上一点,连接 EB,ED.(1)求证:△BEC≌△DEC;(2)延长BE 交AD于点F,若∠DEB=140°,求∠AFE 的度数.图 4-3-34(1)证明:∵四边形 ABCD 是正方形,
∴CD=CB,∠DCA=∠BCA,
又∵CE=CE ,∴ △BEC≌△DEC.(2)解:∵∠DEB=140°,又∵△BEC≌△DEC,
∴∠DEC=∠BEC=70°.
∴∠AEF=∠BEC=70°.∵∠DAB=90°,∴∠DAC=∠BAC=45°.
∴∠AFE=180°-70°-45°=65°.
即∠AFE 的度数是 65°.
的关系.
2.掌握四边形是矩形、菱形、正方形的条件.
3.了解矩形的重心及物理意义(如一根均匀木棒、一块均
匀的矩形木板的重心).四个角都
是直角轴对称,
中心对称考点1特殊平行四边形的性质和判定考点2特殊平行四边形之间的关系及相互转化如图4-3-19.
图 4-3-19考点 3四边形的有关计算1.矩形面积=长×宽.
2.平行四边形面积=底×高.
1
2
1
23.菱形面积=底×高=—×两条对角线的积.
4.正方形面积=边长×边长=—×两条对角线的积.【学有奇招】1.口诀.(1)矩形的判定:任意一个四边形,三个直角成矩形;对角线等互平分,四边形它是矩形.已知平行四边形,一个直角叫矩形;两对角线若相等,理所当然为矩形.(2)菱形的判定:任意一个四边形,四边相等成菱形;四边形的对角线,垂直平分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.2.一般证明正方形的步骤是先证四边形是矩形或菱形.)1.矩形、菱形、正方形都具有的性质是(
A.对角线相等BB.对角线互相平分
C.对角线平分一组对角
D.对角线互相垂直2.如图 4-3-20,在矩形 ABCD 中,对角线 AC,BD 相交于点 O,若∠AOB=60°,AB=4 cm,则 AC 的长为()BA.4 cmB.8 cmC.12 cmD.4cm 图 4-3-20图 4-3-21 3.如图 4-3-21,两个完全相同的三角尺 ABC 和 DEF 在直
线 l 上滑动.要使四边形 CBFE 为菱形,还需添加的一个条件是_____________________________________(写出一个即可).答案不唯一,如:CB=BF或BE⊥CF 4.图 4-3-22 是 4×4 的正方形网格,每个小正方形的顶点
称为格点,每个小正方形的边长均为 1,在每个网格中标注了 5
个格点.在图中以格点为顶点画一个正方形,使其内部已标注
的格点只有 3 个,且边长为无理数.图 19图 4-3-22
解:如图 19. 菱形的性质与判定
例题:(2013 年湖北宜昌)如图 4-3-23,点 E,F 分别是锐角
∠A 两边上的点,AE=AF;分别以点 E,F 为圆心,以 AE 的
长为半径画弧,两弧相交于点 D,连接 DE,DF.
(1)请你判断所画四边形的形状,
并说明理由;
(2)连接 EF,若 AE=8 厘米,∠A=60°,求线段 EF 的长.图 4-3-23解:(1) 四边形AEDF 为菱形.理由:由尺规作图的过程,可知 AE=AF=ED=DF.
(2)连接EF.∵AE=AF,∠A=60°,
∴△EAF 为等边三角形.
∴EF=AE=8 厘米.【试题精选】
1.(2013 年福建泉州) 如图 4-3-24,菱形ABCD的周长为8,对角线AC 和BD 相交于点O,AC∶BD=1∶2,则AO∶ BO=________,菱形 ABCD 的面积 S=__________.
图 4-3-24答案:1∶216 2.(2013 年四川遂宁)如图4-3-25,已知四边形 ABCD 是平行
四边形,DE⊥AB,DF⊥BC,垂足分别是 E,F,并且 DE=DF.
求证:(1)△ADE≌△CDF;(2)四边形 ABCD 是菱形.图 4-3-25证明:(1)∵DE⊥AB,DF⊥BC,
∴∠AED=∠CFD=90°.
∵四边形 ABCD 是平行四边形,∴∠A=∠C.
∠AED=∠CFD,
在△AED 和△CFD 中, ∠A=∠C,
DE=DF,
∴△AED≌△CFD(AAS).(2)∵△AED≌△CFD,∴AD=CD.
∵四边形 ABCD 是平行四边形,
∴四边形 ABCD 是菱形. 名师点评:菱形的性质可以用于证明线段相等、角相等、
直线平行、垂直等,常与三角形全等、勾股定理、方程相结合
进行相关问题的计算与证明. 矩形的性质与判定
3.(2013 年四川资阳)在矩形 ABCD 中,对角线 ACBD 相交于点 O,若∠AOB=60°,AC=10,则 AB=_____.5 4.(2013 年云南大理)如图 4-3-26,已知在△ABC 中,AB
=AC=5,BC=6,AD 是 BC 边上的中线,四边形 ADBE 是平
行四边形.
(1)求证:四边形 ADBE 是矩形;
(2)求矩形 ADBE 的面积.
图 4-3-26(1)证明:∵AB=AC,AD 是 BC 边上的中线,
∴AD⊥BC,∴∠ADB=90°.∵四边形 ADBE 是平行四边形,
∴平行四边形 ADBE 是矩形. 名师点评:矩形的四个角为直角,常将矩形转化为直角三
角形, 矩形的对角线将矩形分成四个等腰(全等)三角形,这些
及矩形性质是证明线段、角相等以及线段平行、垂直的重要依
据. 正方形的性质与判定
例题:(2013 年湖北鄂州)如图 4-3-27,正方形ABCD的边
长为 4,E,F 分别为 DC,BC 的中点.
(1)求证:△ADE≌△ABF;(2)求△AEF 的面积.图 4-3-27【试题精选】 5.(2013 年福建厦门)如图 4-3-28,在正方形 ABCD 中,点
G 是边 BC 上的任意一点,DE⊥AG,垂足为 E,延长 DE 交 AB
于点 F.在线段 AG 上取点 H,使得 AG=DE+HG,连接 BH.求
证:∠ABH=∠CDE.图 4-3-28证明:∵四边形 ABCD 是正方形,∴∠FAD =90°.
∵DE⊥AG,∴∠AED=90°.∴∠FAG +∠EAD=∠ADF+∠EAD.
∴∠FAG =∠ADF.∵AG=DE+HG=AH+HG,∴DE=AH.
又 AD=AB,∴ △ADE≌△BAH.∴∠ABH=∠DAE.∴∠AHB=∠AED=90°.∵∠ADC=90°,∴∠BAH+∠ABH=∠ADF+∠CDE.
∴∠ABH=∠CDE. 名师点评:与正方形有关的计算及推理题常与三角形的全
等、勾股定理、方程、三角函数相联系,有关正方形的判定方
法较多,一般在矩形、菱形的基础上,从边、角、对角线三个
方向进一步分析、判断与证明.1.(2013 年广东茂名)如图 4-3-29,矩形 ABCD 的两条对角线相交于点O,∠AOD=60°,AD=2,则AC 的长是()A.2B.4C.2D.4B图 4-3-29 2.(2013 年广东深圳)如图 4-3-30,有一张一个角为 30°、
最小边长为 2 的直角三角形纸片,沿图中所示的中位线剪开后,)将两部分拼成一个四边形,所得四边形的周长是(
图 4-3-30D 3.(2013 年广东珠海)如图 4-3-31,正方形 ABCD 的边长为
1 , 顺次连接正方形ABCD四边的中点得到第一个正方形
A1B1C1D1,又顺次连接正方形 A1B1C1D1 四边中点得到第二个正
方形 A2B2C2D2,…,以此类推,则第六个正方形 A6B6C6D6 周长
是________.图 4-3-31答案:1
2 4.(2013 年广东广州)如图 4-3-32,四边形 ABCD 是菱形,
对角线 AC 与 BD 相交于 O,AB=5,AO=4,求 BD 的长.图 4-3-32解:∵四边形 ABCD 是菱形,
∴AC⊥BD,且 BO=DO.在 Rt△AOB 中,∵AB=5,AO=4,
由勾股定理,得 BO=3.∴BD=6. 5.(2013 年广东梅州)如图4-3-33,在四边形 ABFC 中,
∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,
且CF=AE.(1)求证:四边形 BECF 是菱形;(2)若四边形 BECF 为正方形,求∠A 的度数.图 4-3-33(1)证明:∵BC 的垂直平分线 EF 交 BC 于点 D,
∴BF=CF,BE=CE.∴E 为 AB 中点,即 BE=AE.
∵CF=AE,∴CF=BE.
∴CF=BF=BE=CE.
∴四边形 BECF 是菱形.(2)解:如图20,∵四边形BECF为正方形,∴∠BEC=90°.又 AE=CE,∴∠A=45°.图 206.(2011 年广东肇庆)如图4-3-34,在正方形ABCD 中,E为对角线 AC 上一点,连接 EB,ED.(1)求证:△BEC≌△DEC;(2)延长BE 交AD于点F,若∠DEB=140°,求∠AFE 的度数.图 4-3-34(1)证明:∵四边形 ABCD 是正方形,
∴CD=CB,∠DCA=∠BCA,
又∵CE=CE ,∴ △BEC≌△DEC.(2)解:∵∠DEB=140°,又∵△BEC≌△DEC,
∴∠DEC=∠BEC=70°.
∴∠AEF=∠BEC=70°.∵∠DAB=90°,∴∠DAC=∠BAC=45°.
∴∠AFE=180°-70°-45°=65°.
即∠AFE 的度数是 65°.
同课章节目录
