2014年中考数学总复习提能训练课件专题八三角形和四边形
文档属性
| 名称 | 2014年中考数学总复习提能训练课件专题八三角形和四边形 |

|
|
| 格式 | zip | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 00:00:00 | ||
图片预览




文档简介
课件11张PPT。专题八 三角形和四边形 在近几年中考中,涌现了大量以三角形、四边形为素材或
背景,或设置有关两三角形全等、相似,或有关特殊三角形、
四边形形状的性质及判定,或借助一定的图形变换(折叠、平移、
旋转、剪拼等)与动态操作,酝酿与构建相关图形的某种状态与
结论,进行相关计算、作图、证明或探究,这对于培养与训练
空间观念、动手操作、合情推理和探究能力等具有重要的作用. 解决这类问题的关键应把握三角形、四边形的性质与特征,
加强相关图形之间的联系,利用所给图形及图形之间形状、大
小、位置关系,进行观察、实验、比较、联想、类比、分析、
综合.从动态、变换操作的角度,运用分类讨论思想分析与解
决有关两个三角形(全等或相似)、特殊三角形、特殊四边形,
进一步体会三角形与四边形之间相互转化、相互依存的内在关
系,从而提高学数学、用数学的能力与素养.在解决此类问题
时要注意:平移、对称、旋转等只是改变了图形的位置,而没
在改变图形的形状与大小.与三角形、四边形有关的计算、证明 例1:(2013 年黑龙江绥化)已知,在△ABC 中,∠BAC=
90°,∠ABC=45°,点 D 为直线 BC 上一动点(点 D 不与点 B,
C 重合).以 AD 为边做正方形 ADEF,连接 CF.(1) 如图Z8-1(1),当点D在线段BC 上时,求证:CF+CD=BC ; (2) 如图 Z8-1(2),当点 D 在线段 BC 的延长线上时,其他
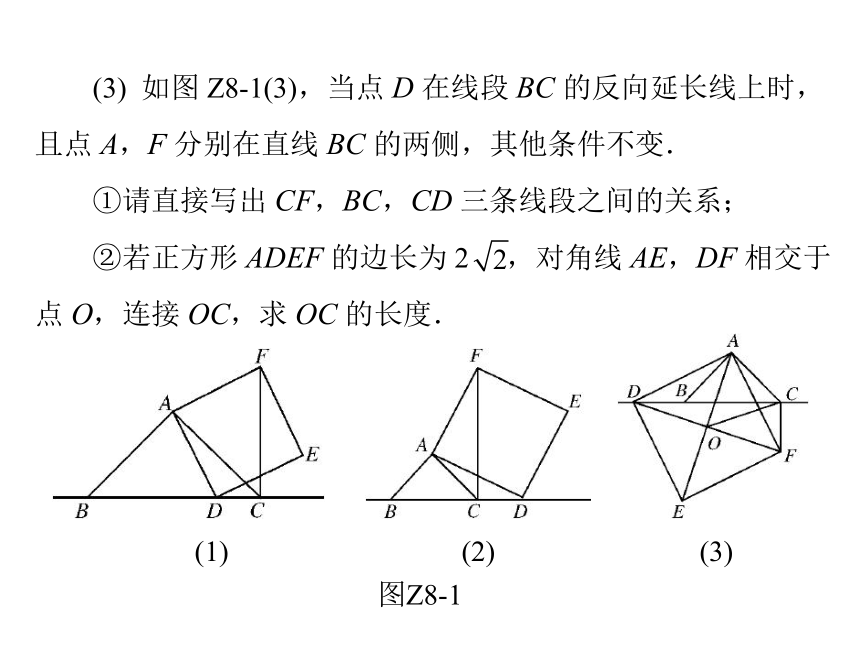
条件不变,请直接写出 CF,BC,CD 三条线段之间的关系; (3) 如图 Z8-1(3),当点 D 在线段 BC 的反向延长线上时,
且点 A,F 分别在直线 BC 的两侧,其他条件不变.
①请直接写出 CF,BC,CD 三条线段之间的关系; ②若正方形 ADEF 的边长为 2
点 O,连接 OC,求 OC 的长度. ,对角线 AE,DF 相交于
(1)(2)(3)图Z8-1 思路分析:由于△ABC 是等腰直角三角形,利用SAS 即可
证明△BAD≌△CAF,从而证得CF=BD,把这种全等(或相似、
平行、垂直、倍分等)的关系类比应用于后续问题,是解动态几
何问题的常用方法.(1)证明:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°.∴AB=AC.∵四边形ADEF 是正方形,∴AD=AF,∠DAF=90°.
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,
∴∠BAD=∠CAF. ∴△BAD≌△CAF.∴BD=CF.
∵BD+CD=BC,∴CF+CD=BC.(2)解:CF-CD=BC.
(3)解:①CD-CF=BC.②∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°.∴AB=AC .∵四边形 ADEF 是正方形,∴AD=AF.∠DAF=90°.
∵∠BAD=90°-∠BAF,∠CAF=90°-∠BAF,∴∠BAD=∠CAF ∴.BAD≌△CAF.∴∠ACF=∠ABD.
∵∠ABC=45°,∴∠ABD=135°.
∴∠ACF=∠ABD=135°.∴∠FCD=90°.∴△FCD 为直角三角形.
名师点评:题目中首先提供某种特殊情形下的结论,然后
将其进行拓展、延伸到一般情况,进一步探究相关结论,解答
此类问题的关键是在于由特殊到一般、由简单到复杂的思维方
式,这类试题不仅结论可以类比,而且思维方法、证明过程也
可通过类比得出.与三角形、四边形有关的操作探究题 例2:(2013 年湖南娄底)某校九年级学习小组在探究学习
过程中,用 2 块完全相同的且含60°角的直角三角板ABC 与AFE
按如图Z8-2(1)所示位置放置,现将Rt△AEF 绕 A 点按逆时针
方向旋转角α(0°<α<90°),如图Z8-2(2),AE 与 BC 交于点M,
AC 与 EF 交于点 N,BC 与 EF 交于点 P.(1)求证:AM=AN;(2)当旋转角α=30°时,四边形ABPF 是什么样的特殊四边形?并说明理由.(1)(2) 图Z8-2
思路分析:(1)要证 AM=AN,只需证明其所在的△ABM 与
△AFN 全等.(2)探究四边形 ABPF 的形状,须抓住旋转角30°,
结合直角三角形中的 60°,30°,90°进行思考四边形的形状.(1)证明:∵∠α+∠EAC=90°,∠NAF+∠EAC=90°,
∴∠α=∠NAF.又∵∠B=∠F,AB=AF,
∴△ABM≌△AFN(AAS).
∴AM=AN.(2)解:四边形ABPF 是菱形.理由如下:
∵∠α=30°,∠EAF=90°,
∴∠BAF=120°.又∵∠B=∠F=60°,∴∠B+∠BAF=60°+120°=180°,∠F+∠BAF=60°+120°=180°.∴AF ∥ BC,AB ∥ EF.∴四边形 ABPF 是平行四边形.
又∵AB=AF,∴?ABPF 是菱形. 名师点评:探究四边形的形状要熟练掌握特殊四边形(平行
四边形、菱形、矩形、正方形)的判定方法,关键是挖掘背景图
形中所含的条件.
背景,或设置有关两三角形全等、相似,或有关特殊三角形、
四边形形状的性质及判定,或借助一定的图形变换(折叠、平移、
旋转、剪拼等)与动态操作,酝酿与构建相关图形的某种状态与
结论,进行相关计算、作图、证明或探究,这对于培养与训练
空间观念、动手操作、合情推理和探究能力等具有重要的作用. 解决这类问题的关键应把握三角形、四边形的性质与特征,
加强相关图形之间的联系,利用所给图形及图形之间形状、大
小、位置关系,进行观察、实验、比较、联想、类比、分析、
综合.从动态、变换操作的角度,运用分类讨论思想分析与解
决有关两个三角形(全等或相似)、特殊三角形、特殊四边形,
进一步体会三角形与四边形之间相互转化、相互依存的内在关
系,从而提高学数学、用数学的能力与素养.在解决此类问题
时要注意:平移、对称、旋转等只是改变了图形的位置,而没
在改变图形的形状与大小.与三角形、四边形有关的计算、证明 例1:(2013 年黑龙江绥化)已知,在△ABC 中,∠BAC=
90°,∠ABC=45°,点 D 为直线 BC 上一动点(点 D 不与点 B,
C 重合).以 AD 为边做正方形 ADEF,连接 CF.(1) 如图Z8-1(1),当点D在线段BC 上时,求证:CF+CD=BC ; (2) 如图 Z8-1(2),当点 D 在线段 BC 的延长线上时,其他
条件不变,请直接写出 CF,BC,CD 三条线段之间的关系; (3) 如图 Z8-1(3),当点 D 在线段 BC 的反向延长线上时,
且点 A,F 分别在直线 BC 的两侧,其他条件不变.
①请直接写出 CF,BC,CD 三条线段之间的关系; ②若正方形 ADEF 的边长为 2
点 O,连接 OC,求 OC 的长度. ,对角线 AE,DF 相交于
(1)(2)(3)图Z8-1 思路分析:由于△ABC 是等腰直角三角形,利用SAS 即可
证明△BAD≌△CAF,从而证得CF=BD,把这种全等(或相似、
平行、垂直、倍分等)的关系类比应用于后续问题,是解动态几
何问题的常用方法.(1)证明:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°.∴AB=AC.∵四边形ADEF 是正方形,∴AD=AF,∠DAF=90°.
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,
∴∠BAD=∠CAF. ∴△BAD≌△CAF.∴BD=CF.
∵BD+CD=BC,∴CF+CD=BC.(2)解:CF-CD=BC.
(3)解:①CD-CF=BC.②∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°.∴AB=AC .∵四边形 ADEF 是正方形,∴AD=AF.∠DAF=90°.
∵∠BAD=90°-∠BAF,∠CAF=90°-∠BAF,∴∠BAD=∠CAF ∴.BAD≌△CAF.∴∠ACF=∠ABD.
∵∠ABC=45°,∴∠ABD=135°.
∴∠ACF=∠ABD=135°.∴∠FCD=90°.∴△FCD 为直角三角形.
名师点评:题目中首先提供某种特殊情形下的结论,然后
将其进行拓展、延伸到一般情况,进一步探究相关结论,解答
此类问题的关键是在于由特殊到一般、由简单到复杂的思维方
式,这类试题不仅结论可以类比,而且思维方法、证明过程也
可通过类比得出.与三角形、四边形有关的操作探究题 例2:(2013 年湖南娄底)某校九年级学习小组在探究学习
过程中,用 2 块完全相同的且含60°角的直角三角板ABC 与AFE
按如图Z8-2(1)所示位置放置,现将Rt△AEF 绕 A 点按逆时针
方向旋转角α(0°<α<90°),如图Z8-2(2),AE 与 BC 交于点M,
AC 与 EF 交于点 N,BC 与 EF 交于点 P.(1)求证:AM=AN;(2)当旋转角α=30°时,四边形ABPF 是什么样的特殊四边形?并说明理由.(1)(2) 图Z8-2
思路分析:(1)要证 AM=AN,只需证明其所在的△ABM 与
△AFN 全等.(2)探究四边形 ABPF 的形状,须抓住旋转角30°,
结合直角三角形中的 60°,30°,90°进行思考四边形的形状.(1)证明:∵∠α+∠EAC=90°,∠NAF+∠EAC=90°,
∴∠α=∠NAF.又∵∠B=∠F,AB=AF,
∴△ABM≌△AFN(AAS).
∴AM=AN.(2)解:四边形ABPF 是菱形.理由如下:
∵∠α=30°,∠EAF=90°,
∴∠BAF=120°.又∵∠B=∠F=60°,∴∠B+∠BAF=60°+120°=180°,∠F+∠BAF=60°+120°=180°.∴AF ∥ BC,AB ∥ EF.∴四边形 ABPF 是平行四边形.
又∵AB=AF,∴?ABPF 是菱形. 名师点评:探究四边形的形状要熟练掌握特殊四边形(平行
四边形、菱形、矩形、正方形)的判定方法,关键是挖掘背景图
形中所含的条件.
同课章节目录
