2014年中考数学总复习提能训练课件专题七函数与图象
文档属性
| 名称 | 2014年中考数学总复习提能训练课件专题七函数与图象 |

|
|
| 格式 | zip | ||
| 文件大小 | 391.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 00:00:00 | ||
图片预览



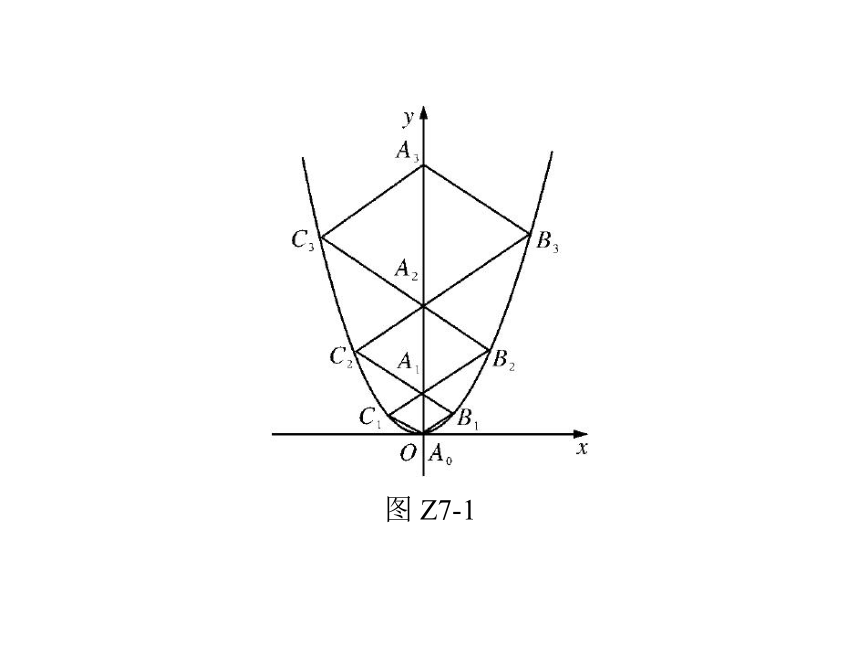




文档简介
课件21张PPT。专题七 函数与图象 函数及其图象是初中数学的重要内容.函数与许多知识有
深刻的内在联系,关联着丰富的几何知识,又是进一步学习的
基础,所以,以函数为背景的问题,题型多变,可谓函数综合
题长盛不衰,实际应用题异彩纷呈,图表分析题形式多样,开
放、探索题方兴未艾,函数在中考中占有重要的地位. 函数与图象常用的数学思想有数形结合思想、分类讨论思
想、函数与方程思想等,中考时常见的题型有图象信息题、代
数几何综合题、函数探索开放型试题、函数创新应用题等,应
用以上数学思想解决函数问题是中考压轴题的首选.例1:(2013年辽宁锦州)二次函数y=—x 的图象如图Z7-1,图象信息题32 2点 A0位于坐标原点,点A1,A2,A3,…,An在y 轴的正半轴上,
点 B1,B2,B3,…,Bn在二次函数位于第一象限的图象上,点
C1,C2,C3,…,Cn 在二次函数位于第二象限的图象上,四边
形 A0B1A1C1,四边形 A1B2A2C2,四边形 A2B3A3C3,…,四边形
An-1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3=…=
∠An-1BnAn=60°,菱形An-1BnAnCn的周长为____________.图 Z7-1
答案:4n 名师点评:本题是二次函数综合题.解题时,利用了二次
函数图象上点的坐标特征,结合菱形的性质,等边三角形的判
定与性质等知识点解题.解答此题的难点是推出第一个等边
△A0B1A1的边长为1,以此类推,求出等边三角形An-1BnAn的边
长为 n.同理可求得△A1B2A2的边长为2……
依此类推,等边三角形An-1BnAn的边长为n,
故菱形An-1BnAnCn的周长为4n. 代数几何综合题
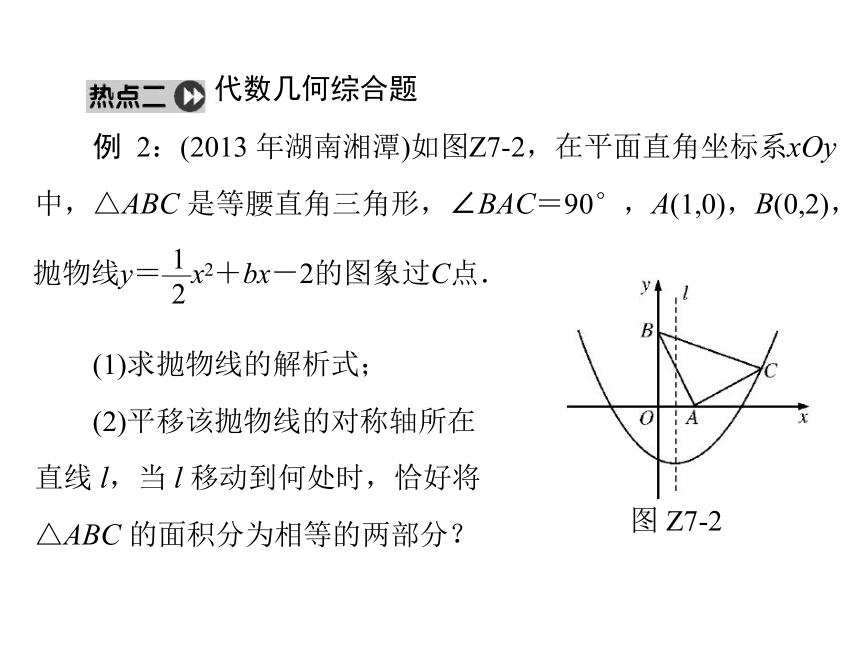
例 2:(2013 年湖南湘潭)如图Z7-2,在平面直角坐标系xOy
中,△ABC 是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),
1
2
(1)求抛物线的解析式;
(2)平移该抛物线的对称轴所在
直线 l,当 l 移动到何处时,恰好将△ABC 的面积分为相等的两部分?图 Z7-2抛物线y=—x2+bx-2的图象过C点. (3)点P 是抛物线上一动点,是否存在点P,使四边形PACB
为平行四边形?若存在,求出 P 点坐标;若不存在,说明理由.
解:(1)如图Z7-3,过点 C 作CD⊥x 轴于点 D,
则∠CAD+∠ACD=90°.
∵∠OBA+∠OAB=90°,∠OAB+∠CAD=90°,
∴∠OAB=∠ACD,∠OBA=∠CAD.
∵在△AOB 与△CDA 中,
∠OAB=∠DCA,AB=CA,
∠OBA=∠DAC,图 Z7-3(3)存在.如图 Z7-4,图Z7-4 过点C 作CG⊥y 轴于点 G,
则CG=OD=3,OG=1,
BG=OB-OG=1.
过点A 作AP∥BC,且AP=BC,连接BP,则四边形PACB
为平行四边形.
理由:过点P 作PH⊥x 轴于点H,则易证△PAH ≌△BCG.
∴PH=BG=1,AH=CG=3.
∴OH=AH-OA=2.∴P(-2,1).当x=-2 时,y=1,即点P 在抛物线上.∴存在符合条件的点P,点P 的坐标为(-2,1). 名师点评:本题是二次函数综合题型,考查了二次函数的
图象与性质、一次函数的图象与性质、待定系数法、全等三角
形、平行四边形、等腰直角三角形等知识点.试题难度不大,
但需要仔细分析,认真计算.函数探索开放题 例3:(2013 年湖南岳阳)如图 Z7-5,已知以 E(3,0)为圆心,
以 5 为半径的⊙E 与 x 轴交于 A,B 两点,与 y 轴交于 C 点,抛
物线 y=ax2+bx+c 经过 A,B,C 三点,顶点为 F.(1)求 A,B,C 三点的坐标;(2)求抛物线的解析式及顶点 F 的坐标;(3)已知 M 为抛物线上一动点(不与 C 点重合),试探究:
①使得以 A,B,M 为顶点的三角形面积与△ABC 的面积相等,求所有符合条件的点 M 的坐标; ②若探究①中的 M 点位于第四象限,连接 M 点与抛物线
顶点 F,试判断直线 MF 与⊙E 的位置关系,并说明理由.图 Z7-5图Z7-6 名师点评:本题是代数几何综合题,主要考查了抛物线与
圆的相关知识,涉及的考点有二次函数的图象与性质、勾股定
理及其逆定理、切线的判定、解一元二次方程等.第(3)①问中,
点 M 在 x 轴上方或下方均可能存在,注意不要漏解.
深刻的内在联系,关联着丰富的几何知识,又是进一步学习的
基础,所以,以函数为背景的问题,题型多变,可谓函数综合
题长盛不衰,实际应用题异彩纷呈,图表分析题形式多样,开
放、探索题方兴未艾,函数在中考中占有重要的地位. 函数与图象常用的数学思想有数形结合思想、分类讨论思
想、函数与方程思想等,中考时常见的题型有图象信息题、代
数几何综合题、函数探索开放型试题、函数创新应用题等,应
用以上数学思想解决函数问题是中考压轴题的首选.例1:(2013年辽宁锦州)二次函数y=—x 的图象如图Z7-1,图象信息题32 2点 A0位于坐标原点,点A1,A2,A3,…,An在y 轴的正半轴上,
点 B1,B2,B3,…,Bn在二次函数位于第一象限的图象上,点
C1,C2,C3,…,Cn 在二次函数位于第二象限的图象上,四边
形 A0B1A1C1,四边形 A1B2A2C2,四边形 A2B3A3C3,…,四边形
An-1BnAnCn都是菱形,∠A0B1A1=∠A1B2A2=∠A2B3A3=…=
∠An-1BnAn=60°,菱形An-1BnAnCn的周长为____________.图 Z7-1
答案:4n 名师点评:本题是二次函数综合题.解题时,利用了二次
函数图象上点的坐标特征,结合菱形的性质,等边三角形的判
定与性质等知识点解题.解答此题的难点是推出第一个等边
△A0B1A1的边长为1,以此类推,求出等边三角形An-1BnAn的边
长为 n.同理可求得△A1B2A2的边长为2……
依此类推,等边三角形An-1BnAn的边长为n,
故菱形An-1BnAnCn的周长为4n. 代数几何综合题
例 2:(2013 年湖南湘潭)如图Z7-2,在平面直角坐标系xOy
中,△ABC 是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),
1
2
(1)求抛物线的解析式;
(2)平移该抛物线的对称轴所在
直线 l,当 l 移动到何处时,恰好将△ABC 的面积分为相等的两部分?图 Z7-2抛物线y=—x2+bx-2的图象过C点. (3)点P 是抛物线上一动点,是否存在点P,使四边形PACB
为平行四边形?若存在,求出 P 点坐标;若不存在,说明理由.
解:(1)如图Z7-3,过点 C 作CD⊥x 轴于点 D,
则∠CAD+∠ACD=90°.
∵∠OBA+∠OAB=90°,∠OAB+∠CAD=90°,
∴∠OAB=∠ACD,∠OBA=∠CAD.
∵在△AOB 与△CDA 中,
∠OAB=∠DCA,AB=CA,
∠OBA=∠DAC,图 Z7-3(3)存在.如图 Z7-4,图Z7-4 过点C 作CG⊥y 轴于点 G,
则CG=OD=3,OG=1,
BG=OB-OG=1.
过点A 作AP∥BC,且AP=BC,连接BP,则四边形PACB
为平行四边形.
理由:过点P 作PH⊥x 轴于点H,则易证△PAH ≌△BCG.
∴PH=BG=1,AH=CG=3.
∴OH=AH-OA=2.∴P(-2,1).当x=-2 时,y=1,即点P 在抛物线上.∴存在符合条件的点P,点P 的坐标为(-2,1). 名师点评:本题是二次函数综合题型,考查了二次函数的
图象与性质、一次函数的图象与性质、待定系数法、全等三角
形、平行四边形、等腰直角三角形等知识点.试题难度不大,
但需要仔细分析,认真计算.函数探索开放题 例3:(2013 年湖南岳阳)如图 Z7-5,已知以 E(3,0)为圆心,
以 5 为半径的⊙E 与 x 轴交于 A,B 两点,与 y 轴交于 C 点,抛
物线 y=ax2+bx+c 经过 A,B,C 三点,顶点为 F.(1)求 A,B,C 三点的坐标;(2)求抛物线的解析式及顶点 F 的坐标;(3)已知 M 为抛物线上一动点(不与 C 点重合),试探究:
①使得以 A,B,M 为顶点的三角形面积与△ABC 的面积相等,求所有符合条件的点 M 的坐标; ②若探究①中的 M 点位于第四象限,连接 M 点与抛物线
顶点 F,试判断直线 MF 与⊙E 的位置关系,并说明理由.图 Z7-5图Z7-6 名师点评:本题是代数几何综合题,主要考查了抛物线与
圆的相关知识,涉及的考点有二次函数的图象与性质、勾股定
理及其逆定理、切线的判定、解一元二次方程等.第(3)①问中,
点 M 在 x 轴上方或下方均可能存在,注意不要漏解.
同课章节目录
