2014年中考数学总复习提能训练课件专题三开放探索题
文档属性
| 名称 | 2014年中考数学总复习提能训练课件专题三开放探索题 |

|
|
| 格式 | zip | ||
| 文件大小 | 178.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:49:58 | ||
图片预览



文档简介
课件9张PPT。专题三 开放探索题 开放探索性试题在中考中越来越受到重视,由于条件或结
论的不确定性,使得解题的方法与答案呈多样性,学生犹如八
仙过海,各显神通. 探索性问题的特点是:问题一般没有明确的条件或结论,
没有固定的形式和方法,需要自己通过观察、分析、比较、概
括、推理、判断等探索活动来确定所需求的结论、条件或方法,
这类题主要考查学生分析问题和解决问题的能力和创新意识.
开放探索题常见的类型有:(1)条件开放型,即问题的条件
不完备或满足结论的条件不唯一;(2)结论开放型,即在给定的
条件下,结论不唯一;(3)策略开放型,即思维策略与解题方法
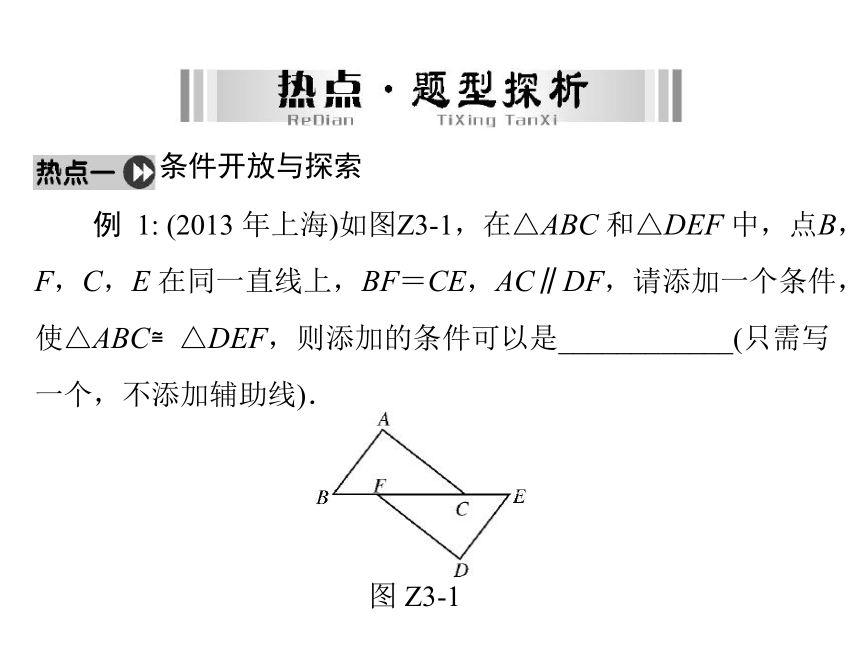
不唯一.条件开放与探索 例 1: (2013 年上海)如图Z3-1,在△ABC 和△DEF 中,点B,
F,C,E 在同一直线上,BF=CE,AC∥DF,请添加一个条件,
使△ABC≌△DEF,则添加的条件可以是____________(只需写
一个,不添加辅助线).图 Z3-1解析:∵BF=CE,B,F,C,E 在同一条直线上,
∴BC=EF.∵AC ∥ DF,∴∠ACB=∠DFE.∴两个三角形中有一个角和一条边分别对应相等.还要再找一个条件(边或角).∴可以补的直接条件有:AC=DF,∠A=∠D,∠B=∠E.
可以补的间接条件有AB ∥ DE.
答案:AB∥DE(答案不唯一) 名师点评:本题考查了全等三角形的判定的应用,是条件
开放题,解题时,先把判断全等三角形的已知条件确定下来,
再利用全等三角形的判定定理SAS,ASA,AAS,SSS 去补充
需要的条件,答案不唯一.结论开放与探索 例2:(2013 年天津)如图 Z3-2,已知∠C=∠D,∠ABC=
∠BAD,AC 与 BD 相交于点 O,请写出图中一组相等的线段
______________.图 Z3-2解析:∵在△ABC 和△BAD 中,∠D=∠C,∠BAD=∠ABC,
AB=BA,∴△ABC≌△BAD(AAS).∴AC=BD,AD=BC.
还可以再证明 OA=OB,OD=OC.
答案:AC=BD(答案不唯一) 名师点评:本题考查了全等三角形的判定与性质,是基础
题,关键在于公共边AB 的应用,这是结论开放型题目,答案
不唯一.策略开放与探索 例3:在一服装厂里有大量形状为等腰直角三角形的边角
布料.现找出其中的一种,测得∠C=90°,AC=BC=4,今要
从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形
的边缘半径恰好都在△ABC 的边上,且扇形的弧与△ABC 的其
他边相切.请设计出所有符合题意的方案示意图,并求出扇形
的半径(只要求画出扇形,并直接写出扇形半径). 解:由题意,可考虑圆心在顶点、直角边和斜边上,设计
出符合题意的方案示意图如图Z3-3 的四种方案:
图Z3-3 名师点评:策略开放题要结合分类讨论思想来解题,先选
择一个分类的标准,再进行讨论解题时做到不重不漏.
论的不确定性,使得解题的方法与答案呈多样性,学生犹如八
仙过海,各显神通. 探索性问题的特点是:问题一般没有明确的条件或结论,
没有固定的形式和方法,需要自己通过观察、分析、比较、概
括、推理、判断等探索活动来确定所需求的结论、条件或方法,
这类题主要考查学生分析问题和解决问题的能力和创新意识.
开放探索题常见的类型有:(1)条件开放型,即问题的条件
不完备或满足结论的条件不唯一;(2)结论开放型,即在给定的
条件下,结论不唯一;(3)策略开放型,即思维策略与解题方法
不唯一.条件开放与探索 例 1: (2013 年上海)如图Z3-1,在△ABC 和△DEF 中,点B,
F,C,E 在同一直线上,BF=CE,AC∥DF,请添加一个条件,
使△ABC≌△DEF,则添加的条件可以是____________(只需写
一个,不添加辅助线).图 Z3-1解析:∵BF=CE,B,F,C,E 在同一条直线上,
∴BC=EF.∵AC ∥ DF,∴∠ACB=∠DFE.∴两个三角形中有一个角和一条边分别对应相等.还要再找一个条件(边或角).∴可以补的直接条件有:AC=DF,∠A=∠D,∠B=∠E.
可以补的间接条件有AB ∥ DE.
答案:AB∥DE(答案不唯一) 名师点评:本题考查了全等三角形的判定的应用,是条件
开放题,解题时,先把判断全等三角形的已知条件确定下来,
再利用全等三角形的判定定理SAS,ASA,AAS,SSS 去补充
需要的条件,答案不唯一.结论开放与探索 例2:(2013 年天津)如图 Z3-2,已知∠C=∠D,∠ABC=
∠BAD,AC 与 BD 相交于点 O,请写出图中一组相等的线段
______________.图 Z3-2解析:∵在△ABC 和△BAD 中,∠D=∠C,∠BAD=∠ABC,
AB=BA,∴△ABC≌△BAD(AAS).∴AC=BD,AD=BC.
还可以再证明 OA=OB,OD=OC.
答案:AC=BD(答案不唯一) 名师点评:本题考查了全等三角形的判定与性质,是基础
题,关键在于公共边AB 的应用,这是结论开放型题目,答案
不唯一.策略开放与探索 例3:在一服装厂里有大量形状为等腰直角三角形的边角
布料.现找出其中的一种,测得∠C=90°,AC=BC=4,今要
从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形
的边缘半径恰好都在△ABC 的边上,且扇形的弧与△ABC 的其
他边相切.请设计出所有符合题意的方案示意图,并求出扇形
的半径(只要求画出扇形,并直接写出扇形半径). 解:由题意,可考虑圆心在顶点、直角边和斜边上,设计
出符合题意的方案示意图如图Z3-3 的四种方案:
图Z3-3 名师点评:策略开放题要结合分类讨论思想来解题,先选
择一个分类的标准,再进行讨论解题时做到不重不漏.
同课章节目录
