2014年中考数学总复习提能训练课件专题十动态问题
文档属性
| 名称 | 2014年中考数学总复习提能训练课件专题十动态问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 197.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:51:02 | ||
图片预览



文档简介
课件11张PPT。专题十 动态问题 动态几何问题就是研究在几何图形的运动中伴随着一定的图
形位置、数量关系的 “变”与 “不变”性.就其运动对象而言,
有 “点动” “线动”和“面动”;就其运动形式而言,有“移
动”“滚动”“旋转”和“翻折”等. 动态几何问题常集几何、代数知识于一体,数形结合,有较
强的综合性,题目灵活多变,动中有静,动静结合,能够在运动
变化过程中发展学生思维和空间想象能力,是中考热点,常在中
考中以压轴题的形式出现. 点动
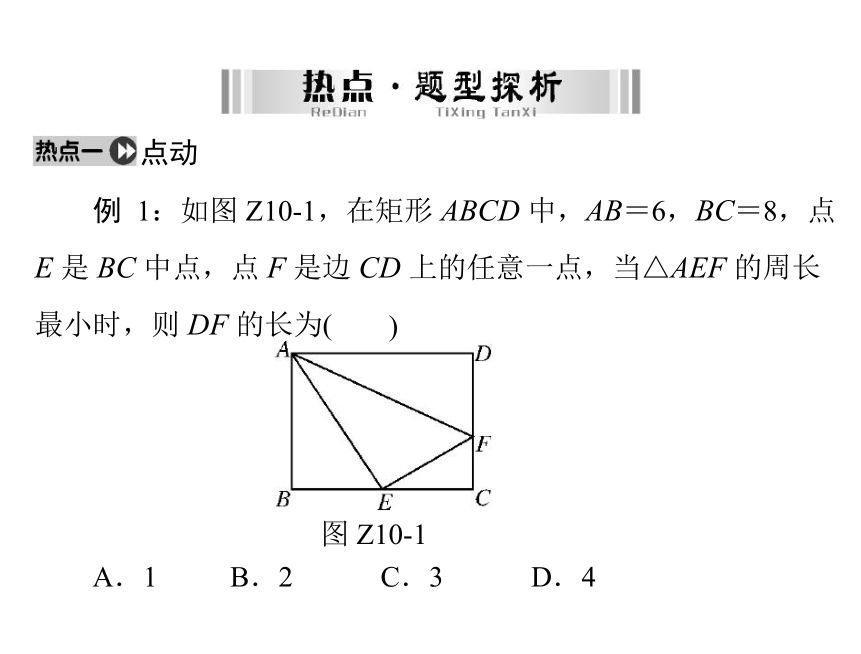
例 1:如图 Z10-1,在矩形 ABCD 中,AB=6,BC=8,点
E 是 BC 中点,点 F 是边 CD 上的任意一点,当△AEF 的周长最小时,则 DF 的长为()图 Z10-1A.1B.2C.3D.4解析:如图Z10-2,作点E 关于直线CD 的对称点E′,连接AE′交CD 于点F,图Z10-2∵在矩形 ABCD 中,AB=6,BC=8,点 E 是 BC 中点,
∴BE=CE=CE′=4.
∵AB⊥BC,CD⊥BC,
答案:D 名师点评:本题考查的是利用轴对称解决最短路线问题及
相似三角形的判定与性质,根据题意作出E 点关于直线CD 的
对称点,再根据轴对称的性质求出CE′的长,利用相似三角形
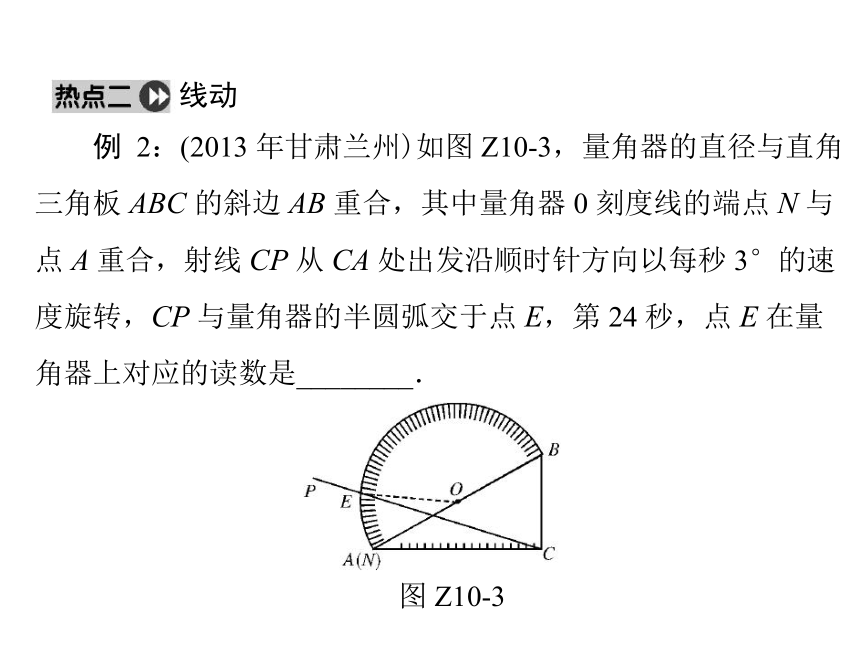
的对应边成比例即可得出结论.线动 例 2:(2013 年甘肃兰州)如图 Z10-3,量角器的直径与直角
三角板 ABC 的斜边 AB 重合,其中量角器 0 刻度线的端点 N 与
点 A 重合,射线 CP 从 CA 处出发沿顺时针方向以每秒 3°的速
度旋转,CP 与量角器的半圆弧交于点 E,第 24 秒,点 E 在量
角器上对应的读数是________.图 Z10-3解析:连接 OE,∵∠ACB=90°,∴A,B,C 在以点O 为圆心,AB 为直径的圆上.
∴点 E,A,B,C 共圆.
∵∠ACE=3×24=72°,
∴∠AOE=2∠ACE=144°.∴点E 在量角器上对应的读数是 144°.
答案:144°名师点评:本题考查的是圆周角定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.面动 例3:(2013 年山东潍坊)如图 Z10-4,将一个边长为 2 的正
方形 ABCD 和一个长为 2、宽为 1 的长方形 CEFD 拼在一起,
构成一个大的长方形 ABEF.现将小长方形 CEFD 绕点 C 按顺时
针旋转至 CE′F′D′,旋转角为α.(1)当点 D′恰好落在 EF 边上时,求旋转角α的值;
(2)如图 Z10-5,G 为 BC 中点,且 0°<α<90°,
求证:GD′=E′D; (3)小长方形 CEFD 绕点C 按顺时针旋转一周的过程中,
△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;
若不能,请说明理由.图 Z10-4图 Z10-5(1)解:∵长方形CEFD 绕点C 顺时针旋转至CE′F′D′,∴CD′=CD=2.在Rt△CED′中,CD′=2,CE=1,∴∠CD′E=30°.
∵CD∥EF,∴∠α=30°.(2)证明:∵G 为BC 中点,∴CG=1.∴CG=CE.
∵长方形CEFD 绕点C 顺时针旋转至CE′F′D′,
∴∠D′CE′=∠DCE=90°.CE=CE′=CG.
∴∠GCD′=∠DCE′=90°+α.CD′=CD,在GCD′ 和DCE′中, ∠GCD′=∠E′CD,CG=CE′,∴△GCD′≌△E′CD(SAS).∴GD′=E′D.=135°;(3)解:能.理由如下:
∵四边形ABCD为正方形,∴CB=CD.
∵CD=CD′,
∴△BCD′与△DCD′为腰相等的两等腰三角形.
当∠BCD′=∠DCD′时,△BCD′≌△DCD′.①当△BCD′与△DCD′为钝角三角形时,α=270°
2
名师点评:本题考查了旋转的性质:旋转前后两图形全等;
对应点到旋转中心的距离相等;对应点与旋转中心的连线段的
夹角等于旋转角.也考查了正方形、矩形的性质以及三角形全
等的判定与性质.
形位置、数量关系的 “变”与 “不变”性.就其运动对象而言,
有 “点动” “线动”和“面动”;就其运动形式而言,有“移
动”“滚动”“旋转”和“翻折”等. 动态几何问题常集几何、代数知识于一体,数形结合,有较
强的综合性,题目灵活多变,动中有静,动静结合,能够在运动
变化过程中发展学生思维和空间想象能力,是中考热点,常在中
考中以压轴题的形式出现. 点动
例 1:如图 Z10-1,在矩形 ABCD 中,AB=6,BC=8,点
E 是 BC 中点,点 F 是边 CD 上的任意一点,当△AEF 的周长最小时,则 DF 的长为()图 Z10-1A.1B.2C.3D.4解析:如图Z10-2,作点E 关于直线CD 的对称点E′,连接AE′交CD 于点F,图Z10-2∵在矩形 ABCD 中,AB=6,BC=8,点 E 是 BC 中点,
∴BE=CE=CE′=4.
∵AB⊥BC,CD⊥BC,
答案:D 名师点评:本题考查的是利用轴对称解决最短路线问题及
相似三角形的判定与性质,根据题意作出E 点关于直线CD 的
对称点,再根据轴对称的性质求出CE′的长,利用相似三角形
的对应边成比例即可得出结论.线动 例 2:(2013 年甘肃兰州)如图 Z10-3,量角器的直径与直角
三角板 ABC 的斜边 AB 重合,其中量角器 0 刻度线的端点 N 与
点 A 重合,射线 CP 从 CA 处出发沿顺时针方向以每秒 3°的速
度旋转,CP 与量角器的半圆弧交于点 E,第 24 秒,点 E 在量
角器上对应的读数是________.图 Z10-3解析:连接 OE,∵∠ACB=90°,∴A,B,C 在以点O 为圆心,AB 为直径的圆上.
∴点 E,A,B,C 共圆.
∵∠ACE=3×24=72°,
∴∠AOE=2∠ACE=144°.∴点E 在量角器上对应的读数是 144°.
答案:144°名师点评:本题考查的是圆周角定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.面动 例3:(2013 年山东潍坊)如图 Z10-4,将一个边长为 2 的正
方形 ABCD 和一个长为 2、宽为 1 的长方形 CEFD 拼在一起,
构成一个大的长方形 ABEF.现将小长方形 CEFD 绕点 C 按顺时
针旋转至 CE′F′D′,旋转角为α.(1)当点 D′恰好落在 EF 边上时,求旋转角α的值;
(2)如图 Z10-5,G 为 BC 中点,且 0°<α<90°,
求证:GD′=E′D; (3)小长方形 CEFD 绕点C 按顺时针旋转一周的过程中,
△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;
若不能,请说明理由.图 Z10-4图 Z10-5(1)解:∵长方形CEFD 绕点C 顺时针旋转至CE′F′D′,∴CD′=CD=2.在Rt△CED′中,CD′=2,CE=1,∴∠CD′E=30°.
∵CD∥EF,∴∠α=30°.(2)证明:∵G 为BC 中点,∴CG=1.∴CG=CE.
∵长方形CEFD 绕点C 顺时针旋转至CE′F′D′,
∴∠D′CE′=∠DCE=90°.CE=CE′=CG.
∴∠GCD′=∠DCE′=90°+α.CD′=CD,在GCD′ 和DCE′中, ∠GCD′=∠E′CD,CG=CE′,∴△GCD′≌△E′CD(SAS).∴GD′=E′D.=135°;(3)解:能.理由如下:
∵四边形ABCD为正方形,∴CB=CD.
∵CD=CD′,
∴△BCD′与△DCD′为腰相等的两等腰三角形.
当∠BCD′=∠DCD′时,△BCD′≌△DCD′.①当△BCD′与△DCD′为钝角三角形时,α=270°
2
名师点评:本题考查了旋转的性质:旋转前后两图形全等;
对应点到旋转中心的距离相等;对应点与旋转中心的连线段的
夹角等于旋转角.也考查了正方形、矩形的性质以及三角形全
等的判定与性质.
同课章节目录
