2014年中考数学总复习提能训练课件专题五方案与设计
文档属性
| 名称 | 2014年中考数学总复习提能训练课件专题五方案与设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 224.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 11:53:41 | ||
图片预览





文档简介
课件14张PPT。专题五 方案与设计 方案与设计问题是指解决问题的方案决策问题,同一个问
题往往有多种不同的解决方案,但其中最科学、最合理的方案
常常仅有一种.随着课程改革的全面展开和逐步深化,有利于
考查学生创新意识和实践能力的方案设计问题已经成为中考命
题的一大热点. 方案设计问题大多取材于生活背景,富有浓厚的生活气息,
能够让学生充分体验数学知识的应用价值,有利于激发学生学
习数学的乐趣和学好数学的动力,因此,这类问题必然在中考
中盛久不衰,它的出现改变了学生以往只依赖于模仿和记忆的
“重结果,轻过程”的学习方式,这不仅有利于培养学生动手
操作和实践活动的能力,更为重要的是能够让学生养成用数学
的意识.图案设计 例 1:(2013 年湖南衡阳)一种电讯信号转发装置的发射直
径为 31 km.现要求:在一边长为 30 km 的正方形城区选择若干
个安装点,每个点安装一个这种转发装置,使这些装置转发的
信号能完全覆盖这个城市.问: (1)能否找到这样的 4 个安装点,使得这些点安装了这种转
发装置后能达到预设的要求?在图 Z5-1(1)中画出安装点的示
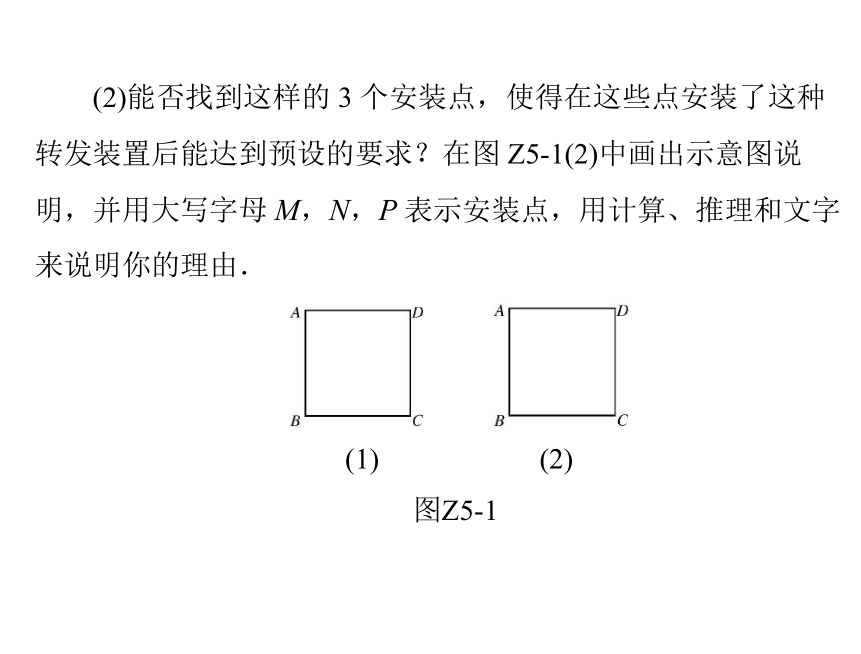
意图,并用大写字母 M,N,P,Q 表示安装点; (2)能否找到这样的 3 个安装点,使得在这些点安装了这种
转发装置后能达到预设的要求?在图 Z5-1(2)中画出示意图说
明,并用大写字母 M,N,P 表示安装点,用计算、推理和文字
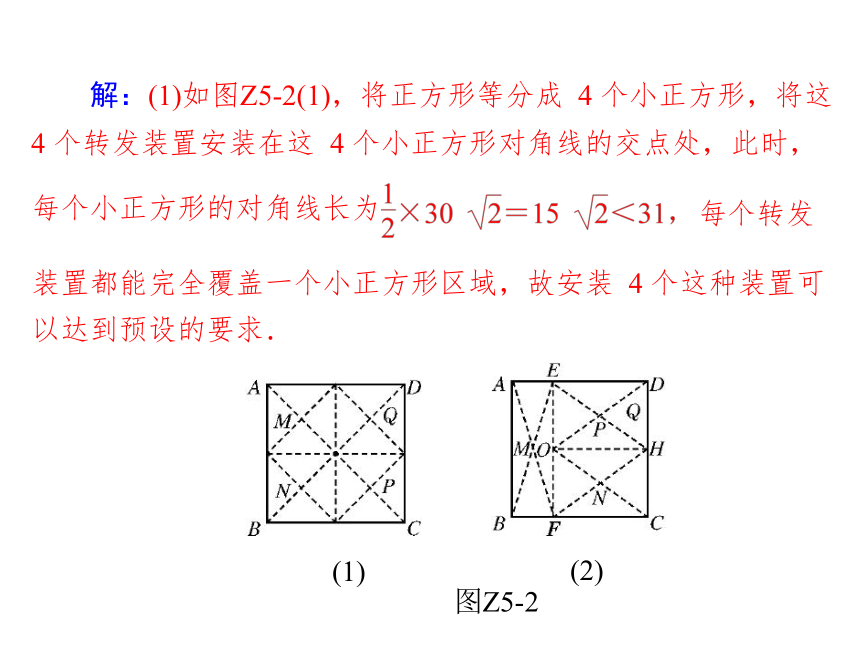
来说明你的理由.(1)(2)图Z5-1每个小正方形的对角线长为 解:(1)如图Z5-2(1),将正方形等分成 4 个小正方形,将这
4 个转发装置安装在这 4 个小正方形对角线的交点处,此时,每个转发装置都能完全覆盖一个小正方形区域,故安装 4 个这种装置可
以达到预设的要求.(1) (2)
图Z5-2 (2)方法一,将原正方形分割成如图 Z5-2(2)中的 3 个矩形,
使得 BE=OD=OC.将每个装置安装在这些矩形的对角线
交点处.
设 AE=x,则 ED=30-x,DH=15,
由 BE=OD,得 x2+302=(30-x)2+152,即如此安装3 个这种转发装置,能达到预设要求. 方法二,将原正方形割成如图Z5-2(2)中的3个矩形,使得
BE=31,H 是CD 的中点,将每个装置安装在这些矩形的对角
线交点处, 即如此安装3 个这个转发装置,也能达到预设要求.
名师点评:考查应用与设计作图.解决本题的关键是先利
用常见图形得到合适的计算方法和思路,然后根据类比方法利
用覆盖的最大距离得到相类似的解.方案设计 例2:(2013 年天津)甲、乙两商场以同样价格出售同样的
商品,并且又各自推出不同的优惠方案:在甲商场累计购物超
过 100 元后,超出 100 元的部分按 90%收费;在乙商场累计购
物超过 50 元后,超出 50 元的部分按 95%收费,设小红在同一
商场累计购物 x 元,其中 x>100.
(1)根据题意,填写下表(单位:元);(2)当 x 取何值时,小红在甲、乙两商场的实际花费相同?
(3)当小红在同一商场累计购物超过 100 元时,在哪家商场的实际花费少?解:(1)在甲商场:100+(290-100)×0.9=271,100+(x-100)×0.9=0.9x+10;在乙商场:50+(290-50)×0.95=278,50+(x-50)×0.95=0.95x+2.5.(2)根据题意,得0.9x+10=0.95x+2.5,
解得x=150.∴当x=150 时,小红在甲、乙两商场的实际花费相同.(3)由 0.9x+10<0.95x+2.5,解得 x>150.
0.9x+10>0.95x+2.5,解得 x<150.
∴当小红累计购物大于 150 上没封顶时,
选择甲商场实际花费少;当小红累计购物超过 100 元而不到 150 元时,
选择乙商场实际花费少;由(1),得当小红累计购物为 150 元时,
选择甲、乙商场花费一样. 名师点评:此题主要考查了一元一次方程的应用和一元一
次不等式的应用,问题较多,且有一定难度.涉及方案选择时
应与方程或不等式相联系.最值问题 例 3:(2012 年山东聊城)某电子厂商投产一种新型电子产
品,每件制造成本为 18 元,试销过程中发现,每月销售量 y(单
位:万件)与销售单价 x(单位:元)之间的关系可以近似地看作
一次函数 y=-2x+100(利润=售价-制造成本).(1)写出每月的利润 z(单位:万元)与销售单价 x(单位:元)之间的函数关系式; (2)当销售单价为多少元时,厂商每月能获得 350 万元的利
润?当销售单价为多少元时,厂商每月能获得最大利润?最大
利润是多少? (3)根据相关部门规定,这种电子产品的销售单价不能高于
32 元,如果厂商要获得每月不低于 350 万元的利润,那么制造
出这种产品每月的最低制造成本需要多少万元?解:(1)z=(x-18)y=(x-18)(-2x+100)
=-2x2+136x- 1800,∴z=-2x2+136x-1800.(2)由 z=350,得 350=-2x2+136x-1800,
解得 x1=25,x2=43.∴当销售单价定为25 元或43 元时,厂商每月能获得350万元的利润. 将z=-2x2+136x-1800 配方,
得z=-2(x-34)2+512.
因此,当销售单价定为34 元时,厂商每月能获得最大利润,
最大利润是512 万元.
(3)结合(2)及函数z=-2x2+136x-1800 的图象(如图 Z5-3)可知,图Z5-3当25≤x≤43 时,z≥350.
又由限价32 元,得25≤x≤32.
根据一次函数的性质,在 y=-2x+100 中y 随x 的增大而减小,∴当 x=32 时,厂商每月制造成本最低,此时,最低成本是 18×(-2×32+100)=648(万元).因此,如果厂商要获得每月不低于350 万元的利润,那么制造出这种产品每月的最低制造成本为648 万元.
题往往有多种不同的解决方案,但其中最科学、最合理的方案
常常仅有一种.随着课程改革的全面展开和逐步深化,有利于
考查学生创新意识和实践能力的方案设计问题已经成为中考命
题的一大热点. 方案设计问题大多取材于生活背景,富有浓厚的生活气息,
能够让学生充分体验数学知识的应用价值,有利于激发学生学
习数学的乐趣和学好数学的动力,因此,这类问题必然在中考
中盛久不衰,它的出现改变了学生以往只依赖于模仿和记忆的
“重结果,轻过程”的学习方式,这不仅有利于培养学生动手
操作和实践活动的能力,更为重要的是能够让学生养成用数学
的意识.图案设计 例 1:(2013 年湖南衡阳)一种电讯信号转发装置的发射直
径为 31 km.现要求:在一边长为 30 km 的正方形城区选择若干
个安装点,每个点安装一个这种转发装置,使这些装置转发的
信号能完全覆盖这个城市.问: (1)能否找到这样的 4 个安装点,使得这些点安装了这种转
发装置后能达到预设的要求?在图 Z5-1(1)中画出安装点的示
意图,并用大写字母 M,N,P,Q 表示安装点; (2)能否找到这样的 3 个安装点,使得在这些点安装了这种
转发装置后能达到预设的要求?在图 Z5-1(2)中画出示意图说
明,并用大写字母 M,N,P 表示安装点,用计算、推理和文字
来说明你的理由.(1)(2)图Z5-1每个小正方形的对角线长为 解:(1)如图Z5-2(1),将正方形等分成 4 个小正方形,将这
4 个转发装置安装在这 4 个小正方形对角线的交点处,此时,每个转发装置都能完全覆盖一个小正方形区域,故安装 4 个这种装置可
以达到预设的要求.(1) (2)
图Z5-2 (2)方法一,将原正方形分割成如图 Z5-2(2)中的 3 个矩形,
使得 BE=OD=OC.将每个装置安装在这些矩形的对角线
交点处.
设 AE=x,则 ED=30-x,DH=15,
由 BE=OD,得 x2+302=(30-x)2+152,即如此安装3 个这种转发装置,能达到预设要求. 方法二,将原正方形割成如图Z5-2(2)中的3个矩形,使得
BE=31,H 是CD 的中点,将每个装置安装在这些矩形的对角
线交点处, 即如此安装3 个这个转发装置,也能达到预设要求.
名师点评:考查应用与设计作图.解决本题的关键是先利
用常见图形得到合适的计算方法和思路,然后根据类比方法利
用覆盖的最大距离得到相类似的解.方案设计 例2:(2013 年天津)甲、乙两商场以同样价格出售同样的
商品,并且又各自推出不同的优惠方案:在甲商场累计购物超
过 100 元后,超出 100 元的部分按 90%收费;在乙商场累计购
物超过 50 元后,超出 50 元的部分按 95%收费,设小红在同一
商场累计购物 x 元,其中 x>100.
(1)根据题意,填写下表(单位:元);(2)当 x 取何值时,小红在甲、乙两商场的实际花费相同?
(3)当小红在同一商场累计购物超过 100 元时,在哪家商场的实际花费少?解:(1)在甲商场:100+(290-100)×0.9=271,100+(x-100)×0.9=0.9x+10;在乙商场:50+(290-50)×0.95=278,50+(x-50)×0.95=0.95x+2.5.(2)根据题意,得0.9x+10=0.95x+2.5,
解得x=150.∴当x=150 时,小红在甲、乙两商场的实际花费相同.(3)由 0.9x+10<0.95x+2.5,解得 x>150.
0.9x+10>0.95x+2.5,解得 x<150.
∴当小红累计购物大于 150 上没封顶时,
选择甲商场实际花费少;当小红累计购物超过 100 元而不到 150 元时,
选择乙商场实际花费少;由(1),得当小红累计购物为 150 元时,
选择甲、乙商场花费一样. 名师点评:此题主要考查了一元一次方程的应用和一元一
次不等式的应用,问题较多,且有一定难度.涉及方案选择时
应与方程或不等式相联系.最值问题 例 3:(2012 年山东聊城)某电子厂商投产一种新型电子产
品,每件制造成本为 18 元,试销过程中发现,每月销售量 y(单
位:万件)与销售单价 x(单位:元)之间的关系可以近似地看作
一次函数 y=-2x+100(利润=售价-制造成本).(1)写出每月的利润 z(单位:万元)与销售单价 x(单位:元)之间的函数关系式; (2)当销售单价为多少元时,厂商每月能获得 350 万元的利
润?当销售单价为多少元时,厂商每月能获得最大利润?最大
利润是多少? (3)根据相关部门规定,这种电子产品的销售单价不能高于
32 元,如果厂商要获得每月不低于 350 万元的利润,那么制造
出这种产品每月的最低制造成本需要多少万元?解:(1)z=(x-18)y=(x-18)(-2x+100)
=-2x2+136x- 1800,∴z=-2x2+136x-1800.(2)由 z=350,得 350=-2x2+136x-1800,
解得 x1=25,x2=43.∴当销售单价定为25 元或43 元时,厂商每月能获得350万元的利润. 将z=-2x2+136x-1800 配方,
得z=-2(x-34)2+512.
因此,当销售单价定为34 元时,厂商每月能获得最大利润,
最大利润是512 万元.
(3)结合(2)及函数z=-2x2+136x-1800 的图象(如图 Z5-3)可知,图Z5-3当25≤x≤43 时,z≥350.
又由限价32 元,得25≤x≤32.
根据一次函数的性质,在 y=-2x+100 中y 随x 的增大而减小,∴当 x=32 时,厂商每月制造成本最低,此时,最低成本是 18×(-2×32+100)=648(万元).因此,如果厂商要获得每月不低于350 万元的利润,那么制造出这种产品每月的最低制造成本为648 万元.
同课章节目录
