2014年中考总复习提能训练课件第六章 第1讲图形的轴对称
文档属性
| 名称 | 2014年中考总复习提能训练课件第六章 第1讲图形的轴对称 |

|
|
| 格式 | zip | ||
| 文件大小 | 1011.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 12:43:02 | ||
图片预览








文档简介
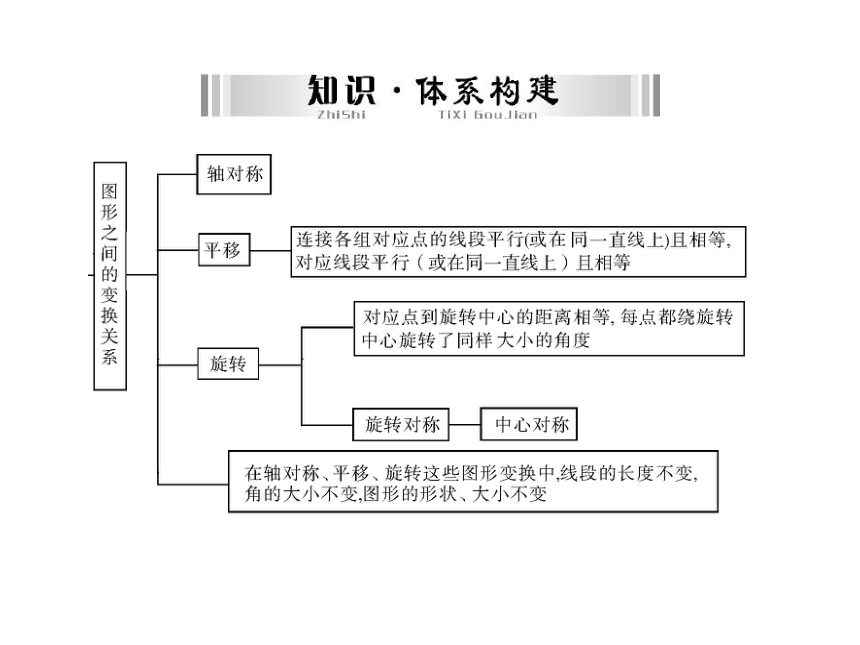
课件32张PPT。第六章 图形与变换第1讲 图形的轴对称、平移与旋转 1.了解轴对称、平移、旋转的概念,理解它们的基本性质.
2.能够按要求作出简单平面图形经过轴对称(或平移、旋
转)后的图形,能作出简单平面图形经过一次或两次轴对称后的
图形.3.能识别轴对称图形和中心对称图形. 4.探索图形之间的变换关系(轴对称、平移、旋转及其组
合);利用轴对称(或平移、旋转)及其组合进行图案设计;认识
和欣赏轴对称(或平移、旋转)在现实生活中的应用.考点1轴对称图形与中心对称图形 1.轴对称图形:如果一个图形沿某条直线对折,对折的两
部分能够完全重合,那么就称这样的图形为轴对称图形,这条直线为__________.对称轴180°对称中心 2.中心对称:把一个图形绕着某一点旋转________,如果
它能够与另一个图形重合,那么这两个图形关于这个点对称或
中心对称,该点叫做____________.考点2变换的概念及性质1.轴对称.相等垂直平分大小对称轴上 (1)定义:把一个图形沿某一条直线翻折过去,如果它能够
与另一个图形重合,那么就称这两个图形关于这条直线对称.
(2)性质:①对应线段相等,对应角______;对称点的连线
被对称轴__________;
②轴对称图形变换的特征是不改变图形的形状和_______,
只改变图形的位置,新旧图形具有对称性;
③轴对称的两个图形,它们对应线段或延长线相交,交点
在____________.2.图形的平移.距离相等平行相等形状 (1)定义:在平面内,将某个图形沿某个方向移动一定的
________,这样的图形运动称为平移.
(2)性质:①平移后,对应线段相等且平行,对应点所连的
线段 ________且________;
②平移后,对应角________且对应角的两边分别平行、方
向相同;
③平移不改变图形的________和大小, 只改变图形的位
置,平移后新旧两个图形全等.角度角度相等相等 3.图形的旋转.
(1)定义:在平面内,将一个图形绕一个定点沿某个方向旋
转一个________,这样的图形运动称为旋转,这个定点称为旋
转中心,转动的________称为旋转角.
(2)特征:在图形旋转过程中,图形上每一个点都绕旋转中
心沿相同方向转动了相同角度;注意每一对对应点与旋转中心
的连线所成的角度都叫旋转角,旋转角都________;对应点到
旋转中心的距离________.【学有奇招】 1.图形的轴对称、平移与旋转不改变图形的大小、形状,
只改变图形的位置,图形变换后与变换前是全等的,解题时必
须牢记这个结论. 2.在处理一些几何问题时,有时不能直接解答,可恰当地
运用旋转、平移、轴对称,使分散、不相关的几何图形重新组
合,将不规则图形转化为规则图形. 3.对称点坐标:对称点坐标要记牢,相反数位置莫混淆,
x 轴对称 y 相反;y 轴对称 x 相反;原点对称最好记,横纵坐标
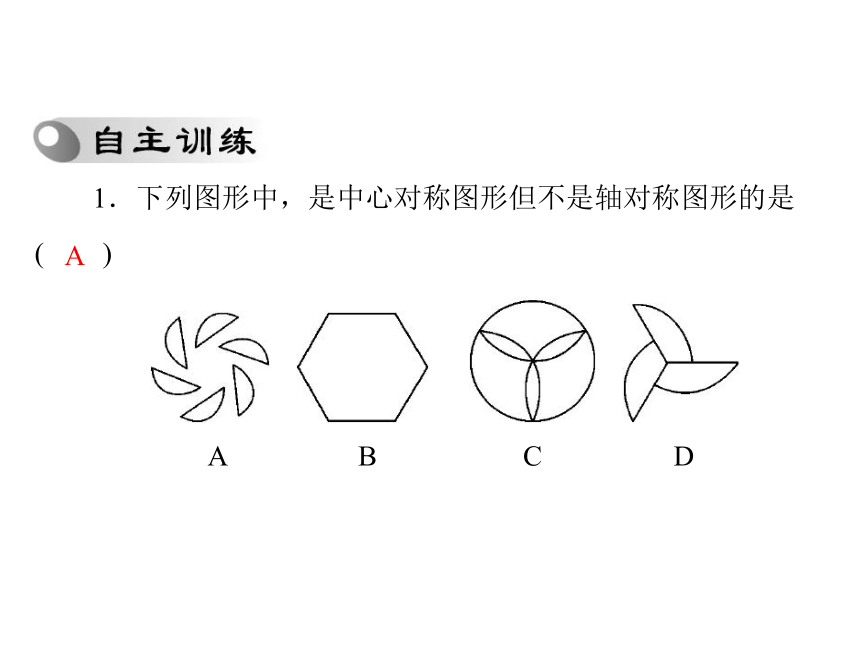
均变号.1.下列图形中,是中心对称图形但不是轴对称图形的是()AABCD 2.如图 6-1-1,在 Rt△ABC 中,∠ACB=90°,∠A=25°,
D 是 AB 上一点,将 Rt△ABC 沿 CD 折叠,使 B 点落在 AC 边)D上的 B′处,则∠ADB′=(
A.25°
B.30°
C.35°D.40°图 6-1-1 3.如图 6-1-2,香港特别行政区区徽是由五个同样的花瓣
组成的,它可以看作是由其中一个花瓣通过怎样的变换而得到的(C )
A.平移
B.轴对称
C.旋转D.先平移, 后旋转图 6-1-2 4.将点 M(3,-2)先向左平移 4 个单位长度,再向上平移
3 个单位长度后得到点 N,则点 N 的坐标是___________.
5.正方形 ABCD 在平面直角坐标系中的位置如图 6-1-3,
将正方形 ABCD 绕点D 按顺时针方向旋转90°后,点B 的坐标为__________.(-1,1)
图 6-1-3(4,0) 轴对称图形、中心对称图形的识别
1.(2013 年四川绵阳)下列“数字”图形中,有且仅有一条对称轴的是()AABCD 2.(2013 年江苏盐城)图 6-1-4(1)是 3×3 正方形方格,将其
中两个方格涂黑,并且使得涂黑后的整个图案是轴对称图形,
约定绕正方形 ABCD 的中心旋转能重合的图案都视为同一种图
案,例如图 6-1-4(2)中的四幅图就视为同一种图案,则得到的不同图案共有()图 6-1-4A.4 种B.5 种C.6 种D.7 种解:如图 33 所示.图 33综上所述,一共有 6 种不同图案.
答案:C 名师点评:判断轴对称图形,关键看对称轴两旁的部分能
够完全重合;判断中心对称图形关键看图形绕某一点旋转180°
后是否与原图形完全重合.x=—.故选 A. 轴对称及应用
3.(2013 年湖南常德)如图 6-1-5,将长方形纸片 ABCD 折
叠,使边 DC 落在对角线 AC 上,折痕为 CE,且 D 点落在 D′处,若 AB=3,AD=4,则 ED=()AA.3
2B. 3C.1D.4
3图 6-1-5 解析:设DE=x,由矩形的性质可知CD=AB=3,由勾股
定理可知AC=5,由折叠可知CD′=CD=3,ED′=ED=x,
∠ED′C=90°,在 Rt△AD′E 中,由勾股定理可得方程(4-x)2=(5-3)2+x2,解得3
2 4.(2013 年江苏苏州)如图6-1-6,在平面直角坐标系中,
Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ),
点 C 的坐标为,点 P 为斜边 OB 上的一动点,则 PA +PC的最小值为()B图 6-1-6 提示:作点 A 关于 OB 的对称点 A′,连接 CA′,与 OB
交于点 P,此时 PA +PC 最小. 名师点评:解决折叠问题的关键:一是折痕两边的折叠部
分全等;二是折叠的某点与所落位置之间的线段被折痕垂直平
分. 图形的平移与旋转
5.(2013 年福建莆田)如图 6-1-7,将 Rt△ABC(其中∠B=
35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1 的位置,使得点 C,A,B1 在同一条直线上,那么旋转角等于()图 6-1-7CA.55°B.70°C.125°D.145° 6.(2013 年浙江温州)如图 6-1-8,在方格纸中,△ABC 的
三个顶点和点 P 都在小方格的顶点上.按要求画一个三角形,
使它的顶点在方格的顶点上.(1)将△ABC 平移,使点 P 落在平移后的三角形内部,在图(1)中画出示意图;(2)以点 C 为旋转中心,将△ABC 旋转,使点 P 落在旋转后的三角形内部,在图(2)中画出示意图.图 6-1-8解:(1)如图 34.图 34(2)如图 35.图 35 名师点评:在平面直角坐标系中,将点(x,y)向右(或左)平
移 a 个单位长度,可以得到对应点(x+a,y)[或(x-a,y)];将
点(x,y)向上(或下)平移 b 个单位长度,可以得到对应点(x,y
+b)[或(x,y-b)].与变换有关的计算题,找准变换中的“变”
与“不变”;借助变换与相关图形的性质进行分析与求解.1.(2013 年广东)下列图形中,不是轴对称图形的是()ABCDC2.(2013 年广东茂名)下列食品商标中,既是轴对称图形又是中心对称图形的是()AABCD 3.(2013年广东广州)如图6-1-9,在 6×6方格中,将图(1)
中的图形 N 平移后的位置如图(2)所示,则图形 N 的平移方法中,正确的是()DA.向下移动 1 格
C. 向上移动 2 格 B. 向上移动 1 格
D. 向下移动 2 格
图 6-1-9 4.(2013 年广东广州)如图6-1-10,Rt△ABC 的斜边 AB=
16, Rt△ABC 绕点 O 顺时针旋转后得到 Rt△A′B′C′,则 Rt
△A ′B′C′的斜边 A′B′上的中线 C′D 的长度为____.
图 6-1-10
5.(2012 年广东肇庆)正方形绕其中心旋转一定的角度与原图形重合,则这个角至少为________度.908 6.(2013 年广东茂名)在格纸上按以下要求作图,不用写作法:
(1)在图 6-1-11 中作出“小旗子”向右平移 6 格后的图案;
(2)在图 6-1-11 中作出“小旗子”绕 O 点按逆时针方向旋转
90°后的图案.图 36 图 6-1-11
解:(1)(2)如图 36 所示. 7.(2013 年广东梅州)如图 6-1-12,在平面直角坐标系中,
A(-2,2),B(-3,-2).
(1)若点C与点A关于原点O对称,则点 C 的坐标为______;
(2)将点 A 向右平移 5 个单位得到
点 D,则点 D 的坐标为________;
(3)由点 A,B,C,D 组成的四
边形 ABCD 内(不包括边界)任取一个
横、纵坐标均为整数的点,求所取的点横、纵坐标之和恰好为零的概率.图 6-1-12= .解:(1)(2,-2)(2)(3,2) (3)如图 37,四边形 ABCD 内(不包括边界)任取一个横、纵
坐标均为整数的点有 15 个,
其中横、纵坐标之和恰好为零的有 3 个,所以所取的点横、纵坐标之和恰好为零的概率是 3 1
15 5图 37 8.(2012 年广东深圳)如图 6-1-13,将矩形 ABCD 沿直线
EF 折叠,使点 C 与点 A 重合,折痕交AD于点 E,交BC 于点
F,连接AF,CE.(1)求证:四边形AFCE为菱形;(2)设AE=a,ED=b,DC=c.请写出一个a,b,c 三者之间的数量关系式.图 6-1-13(1)证明:∵四边形 ABCD 是矩形,∴∠AEF=∠EFC.
由折叠的性质,可得∠AEF=∠CEF,AE=CE,AF=CF.
∴∠EFC=∠CEF.∴CF=CE.∴AF=CF=CE=AE.
∴四边形 AFCE 为菱形.(2)解:a,b,c 三者之间的数量关系式为:a2=b2+c2.
理由:由折叠的性质,得 CE=AE.
∵四边形 ABCD 是矩形,∴∠D=90°.
∵CE=AE=a,ED=b,DC=c,
在 Rt△DCE 中,CE2=CD2+DE2,∴a,b,c 三者之间的数量关系式为:a2=b2+c2.
2.能够按要求作出简单平面图形经过轴对称(或平移、旋
转)后的图形,能作出简单平面图形经过一次或两次轴对称后的
图形.3.能识别轴对称图形和中心对称图形. 4.探索图形之间的变换关系(轴对称、平移、旋转及其组
合);利用轴对称(或平移、旋转)及其组合进行图案设计;认识
和欣赏轴对称(或平移、旋转)在现实生活中的应用.考点1轴对称图形与中心对称图形 1.轴对称图形:如果一个图形沿某条直线对折,对折的两
部分能够完全重合,那么就称这样的图形为轴对称图形,这条直线为__________.对称轴180°对称中心 2.中心对称:把一个图形绕着某一点旋转________,如果
它能够与另一个图形重合,那么这两个图形关于这个点对称或
中心对称,该点叫做____________.考点2变换的概念及性质1.轴对称.相等垂直平分大小对称轴上 (1)定义:把一个图形沿某一条直线翻折过去,如果它能够
与另一个图形重合,那么就称这两个图形关于这条直线对称.
(2)性质:①对应线段相等,对应角______;对称点的连线
被对称轴__________;
②轴对称图形变换的特征是不改变图形的形状和_______,
只改变图形的位置,新旧图形具有对称性;
③轴对称的两个图形,它们对应线段或延长线相交,交点
在____________.2.图形的平移.距离相等平行相等形状 (1)定义:在平面内,将某个图形沿某个方向移动一定的
________,这样的图形运动称为平移.
(2)性质:①平移后,对应线段相等且平行,对应点所连的
线段 ________且________;
②平移后,对应角________且对应角的两边分别平行、方
向相同;
③平移不改变图形的________和大小, 只改变图形的位
置,平移后新旧两个图形全等.角度角度相等相等 3.图形的旋转.
(1)定义:在平面内,将一个图形绕一个定点沿某个方向旋
转一个________,这样的图形运动称为旋转,这个定点称为旋
转中心,转动的________称为旋转角.
(2)特征:在图形旋转过程中,图形上每一个点都绕旋转中
心沿相同方向转动了相同角度;注意每一对对应点与旋转中心
的连线所成的角度都叫旋转角,旋转角都________;对应点到
旋转中心的距离________.【学有奇招】 1.图形的轴对称、平移与旋转不改变图形的大小、形状,
只改变图形的位置,图形变换后与变换前是全等的,解题时必
须牢记这个结论. 2.在处理一些几何问题时,有时不能直接解答,可恰当地
运用旋转、平移、轴对称,使分散、不相关的几何图形重新组
合,将不规则图形转化为规则图形. 3.对称点坐标:对称点坐标要记牢,相反数位置莫混淆,
x 轴对称 y 相反;y 轴对称 x 相反;原点对称最好记,横纵坐标
均变号.1.下列图形中,是中心对称图形但不是轴对称图形的是()AABCD 2.如图 6-1-1,在 Rt△ABC 中,∠ACB=90°,∠A=25°,
D 是 AB 上一点,将 Rt△ABC 沿 CD 折叠,使 B 点落在 AC 边)D上的 B′处,则∠ADB′=(
A.25°
B.30°
C.35°D.40°图 6-1-1 3.如图 6-1-2,香港特别行政区区徽是由五个同样的花瓣
组成的,它可以看作是由其中一个花瓣通过怎样的变换而得到的(C )
A.平移
B.轴对称
C.旋转D.先平移, 后旋转图 6-1-2 4.将点 M(3,-2)先向左平移 4 个单位长度,再向上平移
3 个单位长度后得到点 N,则点 N 的坐标是___________.
5.正方形 ABCD 在平面直角坐标系中的位置如图 6-1-3,
将正方形 ABCD 绕点D 按顺时针方向旋转90°后,点B 的坐标为__________.(-1,1)
图 6-1-3(4,0) 轴对称图形、中心对称图形的识别
1.(2013 年四川绵阳)下列“数字”图形中,有且仅有一条对称轴的是()AABCD 2.(2013 年江苏盐城)图 6-1-4(1)是 3×3 正方形方格,将其
中两个方格涂黑,并且使得涂黑后的整个图案是轴对称图形,
约定绕正方形 ABCD 的中心旋转能重合的图案都视为同一种图
案,例如图 6-1-4(2)中的四幅图就视为同一种图案,则得到的不同图案共有()图 6-1-4A.4 种B.5 种C.6 种D.7 种解:如图 33 所示.图 33综上所述,一共有 6 种不同图案.
答案:C 名师点评:判断轴对称图形,关键看对称轴两旁的部分能
够完全重合;判断中心对称图形关键看图形绕某一点旋转180°
后是否与原图形完全重合.x=—.故选 A. 轴对称及应用
3.(2013 年湖南常德)如图 6-1-5,将长方形纸片 ABCD 折
叠,使边 DC 落在对角线 AC 上,折痕为 CE,且 D 点落在 D′处,若 AB=3,AD=4,则 ED=()AA.3
2B. 3C.1D.4
3图 6-1-5 解析:设DE=x,由矩形的性质可知CD=AB=3,由勾股
定理可知AC=5,由折叠可知CD′=CD=3,ED′=ED=x,
∠ED′C=90°,在 Rt△AD′E 中,由勾股定理可得方程(4-x)2=(5-3)2+x2,解得3
2 4.(2013 年江苏苏州)如图6-1-6,在平面直角坐标系中,
Rt△OAB 的顶点 A 在 x 轴的正半轴上,顶点 B 的坐标为(3, ),
点 C 的坐标为,点 P 为斜边 OB 上的一动点,则 PA +PC的最小值为()B图 6-1-6 提示:作点 A 关于 OB 的对称点 A′,连接 CA′,与 OB
交于点 P,此时 PA +PC 最小. 名师点评:解决折叠问题的关键:一是折痕两边的折叠部
分全等;二是折叠的某点与所落位置之间的线段被折痕垂直平
分. 图形的平移与旋转
5.(2013 年福建莆田)如图 6-1-7,将 Rt△ABC(其中∠B=
35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1 的位置,使得点 C,A,B1 在同一条直线上,那么旋转角等于()图 6-1-7CA.55°B.70°C.125°D.145° 6.(2013 年浙江温州)如图 6-1-8,在方格纸中,△ABC 的
三个顶点和点 P 都在小方格的顶点上.按要求画一个三角形,
使它的顶点在方格的顶点上.(1)将△ABC 平移,使点 P 落在平移后的三角形内部,在图(1)中画出示意图;(2)以点 C 为旋转中心,将△ABC 旋转,使点 P 落在旋转后的三角形内部,在图(2)中画出示意图.图 6-1-8解:(1)如图 34.图 34(2)如图 35.图 35 名师点评:在平面直角坐标系中,将点(x,y)向右(或左)平
移 a 个单位长度,可以得到对应点(x+a,y)[或(x-a,y)];将
点(x,y)向上(或下)平移 b 个单位长度,可以得到对应点(x,y
+b)[或(x,y-b)].与变换有关的计算题,找准变换中的“变”
与“不变”;借助变换与相关图形的性质进行分析与求解.1.(2013 年广东)下列图形中,不是轴对称图形的是()ABCDC2.(2013 年广东茂名)下列食品商标中,既是轴对称图形又是中心对称图形的是()AABCD 3.(2013年广东广州)如图6-1-9,在 6×6方格中,将图(1)
中的图形 N 平移后的位置如图(2)所示,则图形 N 的平移方法中,正确的是()DA.向下移动 1 格
C. 向上移动 2 格 B. 向上移动 1 格
D. 向下移动 2 格
图 6-1-9 4.(2013 年广东广州)如图6-1-10,Rt△ABC 的斜边 AB=
16, Rt△ABC 绕点 O 顺时针旋转后得到 Rt△A′B′C′,则 Rt
△A ′B′C′的斜边 A′B′上的中线 C′D 的长度为____.
图 6-1-10
5.(2012 年广东肇庆)正方形绕其中心旋转一定的角度与原图形重合,则这个角至少为________度.908 6.(2013 年广东茂名)在格纸上按以下要求作图,不用写作法:
(1)在图 6-1-11 中作出“小旗子”向右平移 6 格后的图案;
(2)在图 6-1-11 中作出“小旗子”绕 O 点按逆时针方向旋转
90°后的图案.图 36 图 6-1-11
解:(1)(2)如图 36 所示. 7.(2013 年广东梅州)如图 6-1-12,在平面直角坐标系中,
A(-2,2),B(-3,-2).
(1)若点C与点A关于原点O对称,则点 C 的坐标为______;
(2)将点 A 向右平移 5 个单位得到
点 D,则点 D 的坐标为________;
(3)由点 A,B,C,D 组成的四
边形 ABCD 内(不包括边界)任取一个
横、纵坐标均为整数的点,求所取的点横、纵坐标之和恰好为零的概率.图 6-1-12= .解:(1)(2,-2)(2)(3,2) (3)如图 37,四边形 ABCD 内(不包括边界)任取一个横、纵
坐标均为整数的点有 15 个,
其中横、纵坐标之和恰好为零的有 3 个,所以所取的点横、纵坐标之和恰好为零的概率是 3 1
15 5图 37 8.(2012 年广东深圳)如图 6-1-13,将矩形 ABCD 沿直线
EF 折叠,使点 C 与点 A 重合,折痕交AD于点 E,交BC 于点
F,连接AF,CE.(1)求证:四边形AFCE为菱形;(2)设AE=a,ED=b,DC=c.请写出一个a,b,c 三者之间的数量关系式.图 6-1-13(1)证明:∵四边形 ABCD 是矩形,∴∠AEF=∠EFC.
由折叠的性质,可得∠AEF=∠CEF,AE=CE,AF=CF.
∴∠EFC=∠CEF.∴CF=CE.∴AF=CF=CE=AE.
∴四边形 AFCE 为菱形.(2)解:a,b,c 三者之间的数量关系式为:a2=b2+c2.
理由:由折叠的性质,得 CE=AE.
∵四边形 ABCD 是矩形,∴∠D=90°.
∵CE=AE=a,ED=b,DC=c,
在 Rt△DCE 中,CE2=CD2+DE2,∴a,b,c 三者之间的数量关系式为:a2=b2+c2.
同课章节目录
