2014年中考总复习提能训练课件第六章 第2讲视图与投影
文档属性
| 名称 | 2014年中考总复习提能训练课件第六章 第2讲视图与投影 |

|
|
| 格式 | zip | ||
| 文件大小 | 493.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 12:44:42 | ||
图片预览




文档简介
课件21张PPT。第2讲视图与投影 1.会画基本几何体(直棱柱、圆柱、圆锥、球)的三视图(主
视图、左视图、俯视图),会判断简单物体的三视图,能根据三
视图描述基本几何体或实物原型.
2.了解直棱柱、圆锥的侧面展开图,能根据展开图判断和
制作立体模型.考点1三视图1.三视图的概念.正面上面左面(1)主视图:从________看到的图形.
(2)俯视图:从________看到的图形.
(3)左视图:从________看到的图形.2.三视图的对应关系.长相等高相等宽相等(1)长对正:主视图与俯视图的__________,且相互对正.
(2)高平齐:主视图与左视图的__________,且相互平齐.
(3)宽相等:俯视图与左视图的__________,且相互平行.考点2常见几何体的三视图正方形矩形1.正方体的三视图都是________.圆三角形2.圆柱的三视图有两个是________,另一个是_______.
3.圆锥的三视图中有两个是_______,另一个是________.4.球的三视图都是______.圆圆考点3投影投影平行同一点(点光源) 1.投影:在光线照射下,物体在某个平面(地面、墙壁等)
上留下的影子叫做物体的________.
2.平行投影:由________光线形成的投影.
3.中心投影:由_______________发出的光线形成的投影.【学有奇招】 1.解决三视图问题:首先应该清楚常见图形的三视图是怎
么形成的;其次,对于稍复杂的物体,要将其简化为几个简单
的图形;最后,由三视图判断物体的形状,一般要从三个方向
先判断每一个方向上所能判断的物块数量,然后进行叠加组合
确定物体的形状. 2.解决投影问题时,首先应该根据题意,分清楚是点光源
还是平行光源:①如果是点光源(常见的如灯泡),其影长、位
置不同,所组成的三角形也不同,根据解直角三角形相关知识
进行求解;②如果是平行光源(如太阳光),其影长与物高成正
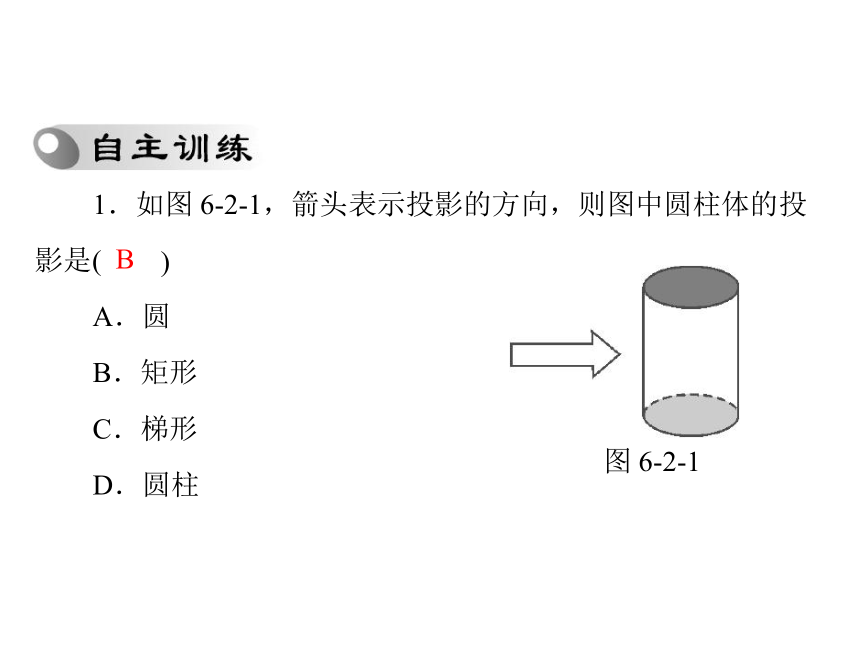
比例,根据相似知识进行求解.1.如图 6-2-1,箭头表示投影的方向,则图中圆柱体的投影是()B图 6-2-1A.圆
B.矩形
C.梯形
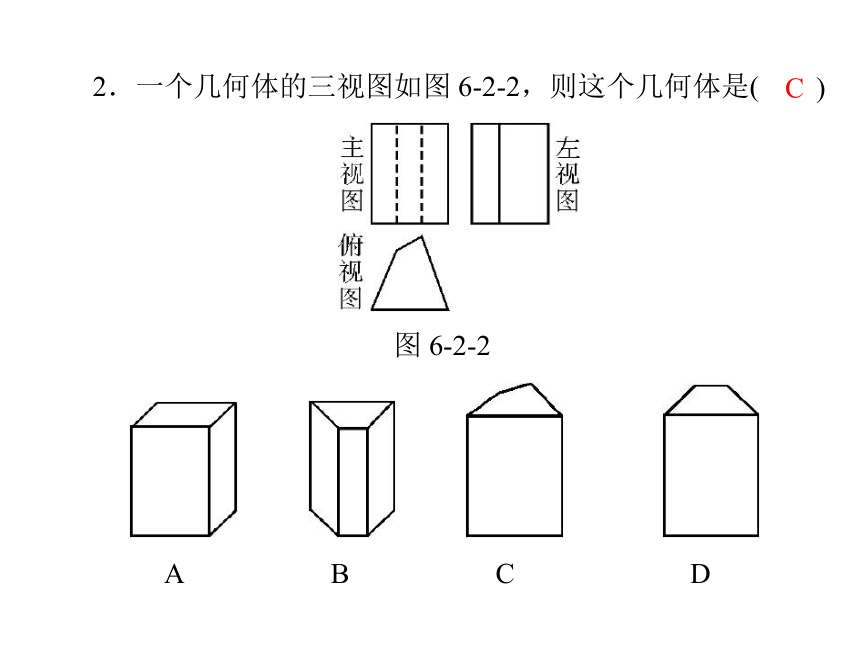
D.圆柱2.一个几何体的三视图如图 6-2-2,则这个几何体是()图 6-2-2CABCD 3.小刚身高1.7 m,测得他站立在阳光下的影子长为0.85 m,
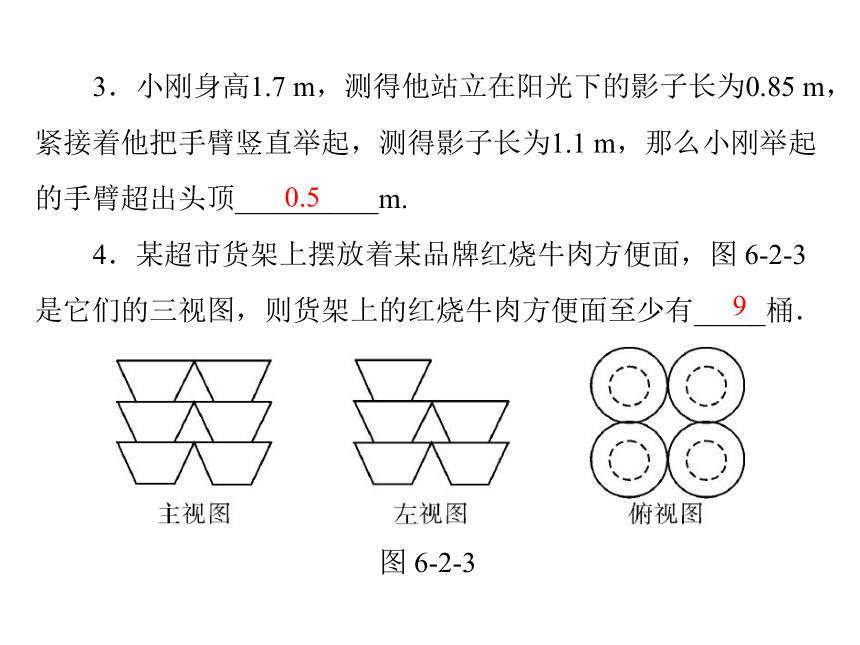
紧接着他把手臂竖直举起,测得影子长为1.1 m,那么小刚举起的手臂超出头顶__________m.0.59 4.某超市货架上摆放着某品牌红烧牛肉方便面,图 6-2-3
是它们的三视图,则货架上的红烧牛肉方便面至少有_____桶.
图 6-2-3 几何体与三视图
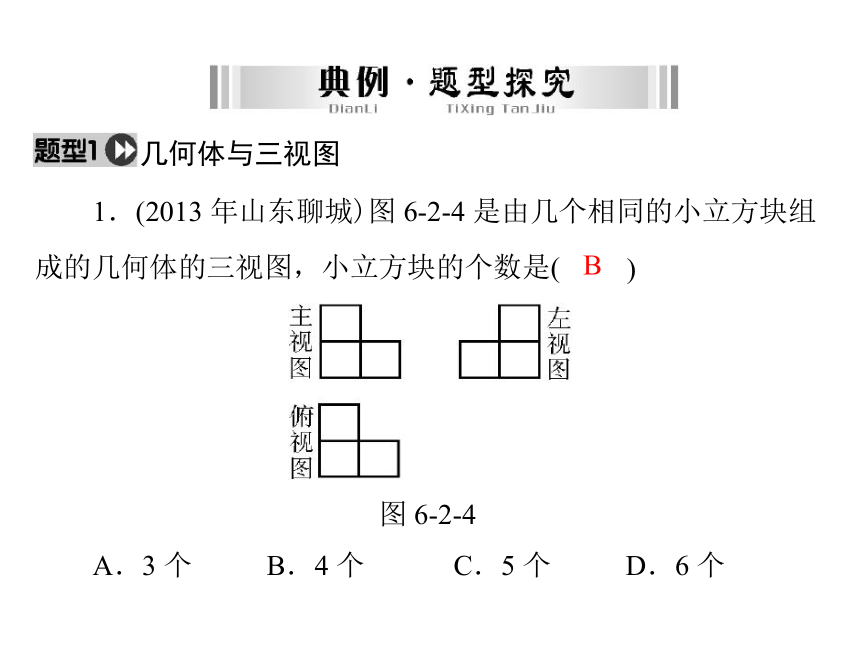
1.(2013 年山东聊城)图 6-2-4 是由几个相同的小立方块组)B成的几何体的三视图,小立方块的个数是(
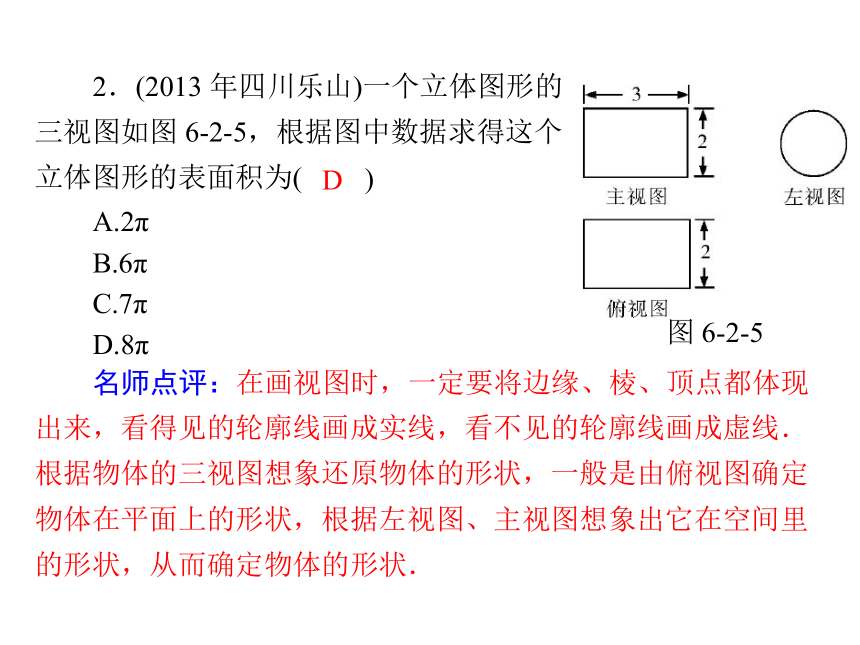
图 6-2-4A.3 个B.4 个C.5 个D.6 个 2.(2013 年四川乐山)一个立体图形的
三视图如图 6-2-5,根据图中数据求得这个)图 6-2-5立体图形的表面积为(
A.2π
B.6π
C.7π
D.8π 名师点评:在画视图时,一定要将边缘、棱、顶点都体现
出来,看得见的轮廓线画成实线,看不见的轮廓线画成虚线.
根据物体的三视图想象还原物体的形状,一般是由俯视图确定
物体在平面上的形状,根据左视图、主视图想象出它在空间里
的形状,从而确定物体的形状.D 几何体的展开图
3.(2013 年湖北随州)图 6-2-6 是一个长方体形状包装盒的
表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)()DA.40×40×70
B. 70×70×80
C. 80×80×40D. 40×70×80图 6-2-6 4.(2013 年四川自贡)如图 6-2-7,将一张边长为 3 的正方
形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,)A这个棱柱的侧面积为(
A.9-3
B.9C.9-5
2D.9-3
2图 6-2-7 投影
5.(2013 年四川达州)图 6-2-8 是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是()(1)(2)(3)(4)图 6-2-8A.(3)(1)(4)(2)
C.(3)(4)(1)(2)B.(3)(2)(1)(4)
D.(2)(4)(1)(3) 解析:观察四幅图根据影子的方向可知,(3)与(4)是建筑物
在上午时的影子,(1)与(2)是建筑物在下午时的影子,再根据影
子的长短可知 (3)早于(4) , (1)早于(2) , 整个先后顺序为
(3)(4)(1)(2).答案:C 6.(2013 年山东济宁)如图 6-2-9,放映幻灯时,通过光源,
把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为
20 cm,到屏幕的距离为 60 cm,且幻灯片中图形的高度为 6 cm,则屏幕上图形的高度为________cm.
图 6-2-9
图4118 名师点评:与中心投影有关的试题,主要涉及两个方面:
一是根据影子确定光源;二是根据相似的知识求影子的长.与
平行投影有关的试题,关键是紧扣光线平行.1.(2013 年广东湛江)图 6-2-10 是由 6 个大小相同的正方体组成的几何体,它的左视图是()A图 6-2-10ABCD2.(2013 年广东茂名) 如图 6-2-11,由两个相同的正方体)D和一个圆锥体组成一个立体图形,其俯视图是(
图 6-2-11ABCD3.(2012 年广东肇庆)图 6-2-12 是某几何体的三视图,则该几何体是()AA.圆锥
C.三棱柱 B.圆柱
D.三棱锥
图 6-2-12 4.(2012 年广东梅州)春蕾数学兴趣小组用一块正方形木板
在阳光下做投影实验,这块正方形木板在地面上形成的投影可
能是______________(写出符合题意的两个图形即可).
5.(2011 年广东广州)由5个棱长为1的正方体组成图 6-2-13所示的几何体.正方形、菱形522 (1)该几何体的体积是_____(立方单位),表面积是_____(平
方单位);
(2)画出该几何体的主视图和左视图.答案:略图 6-2-13 6.(2013 年广东深圳)如图 6-2-14,该小组发现 8 米高的旗
杆 DE 的影子 EF 落在了包含一圆弧型小桥在内的路上,于是他
们开展了测算小桥所在圆的半径的活动.小刚身高 1.6 米,测
得其影长为 2.4 米,同时测得 EG 的长为 3 米,HF 的长为 1 米,
测得拱高(弧 GH 的中点到弦 GH 的距离,即 MN 的长)为 2 米,
求小桥所在圆的半径.图 6-2-14=解:∵小刚身高 1.6 米,测得其影长为 2.4 米,由相似得DE 1.6
EF 2.4,解得 EF=12.∵EG=3,HF=1,∴GH=EF-EG-HF=8.
1
2
设半径 OG=R,则 OM=R-2.
在 Rt△OMG 中,由勾股定理,得
OM2+MG2=OG2.
即(R-2)2+42=R2,解得 R=5.
因此小桥所在的半径为 5 米.由垂径定理,得GM=—GH=4,又MN=2,
视图、左视图、俯视图),会判断简单物体的三视图,能根据三
视图描述基本几何体或实物原型.
2.了解直棱柱、圆锥的侧面展开图,能根据展开图判断和
制作立体模型.考点1三视图1.三视图的概念.正面上面左面(1)主视图:从________看到的图形.
(2)俯视图:从________看到的图形.
(3)左视图:从________看到的图形.2.三视图的对应关系.长相等高相等宽相等(1)长对正:主视图与俯视图的__________,且相互对正.
(2)高平齐:主视图与左视图的__________,且相互平齐.
(3)宽相等:俯视图与左视图的__________,且相互平行.考点2常见几何体的三视图正方形矩形1.正方体的三视图都是________.圆三角形2.圆柱的三视图有两个是________,另一个是_______.
3.圆锥的三视图中有两个是_______,另一个是________.4.球的三视图都是______.圆圆考点3投影投影平行同一点(点光源) 1.投影:在光线照射下,物体在某个平面(地面、墙壁等)
上留下的影子叫做物体的________.
2.平行投影:由________光线形成的投影.
3.中心投影:由_______________发出的光线形成的投影.【学有奇招】 1.解决三视图问题:首先应该清楚常见图形的三视图是怎
么形成的;其次,对于稍复杂的物体,要将其简化为几个简单
的图形;最后,由三视图判断物体的形状,一般要从三个方向
先判断每一个方向上所能判断的物块数量,然后进行叠加组合
确定物体的形状. 2.解决投影问题时,首先应该根据题意,分清楚是点光源
还是平行光源:①如果是点光源(常见的如灯泡),其影长、位
置不同,所组成的三角形也不同,根据解直角三角形相关知识
进行求解;②如果是平行光源(如太阳光),其影长与物高成正
比例,根据相似知识进行求解.1.如图 6-2-1,箭头表示投影的方向,则图中圆柱体的投影是()B图 6-2-1A.圆
B.矩形
C.梯形
D.圆柱2.一个几何体的三视图如图 6-2-2,则这个几何体是()图 6-2-2CABCD 3.小刚身高1.7 m,测得他站立在阳光下的影子长为0.85 m,
紧接着他把手臂竖直举起,测得影子长为1.1 m,那么小刚举起的手臂超出头顶__________m.0.59 4.某超市货架上摆放着某品牌红烧牛肉方便面,图 6-2-3
是它们的三视图,则货架上的红烧牛肉方便面至少有_____桶.
图 6-2-3 几何体与三视图
1.(2013 年山东聊城)图 6-2-4 是由几个相同的小立方块组)B成的几何体的三视图,小立方块的个数是(
图 6-2-4A.3 个B.4 个C.5 个D.6 个 2.(2013 年四川乐山)一个立体图形的
三视图如图 6-2-5,根据图中数据求得这个)图 6-2-5立体图形的表面积为(
A.2π
B.6π
C.7π
D.8π 名师点评:在画视图时,一定要将边缘、棱、顶点都体现
出来,看得见的轮廓线画成实线,看不见的轮廓线画成虚线.
根据物体的三视图想象还原物体的形状,一般是由俯视图确定
物体在平面上的形状,根据左视图、主视图想象出它在空间里
的形状,从而确定物体的形状.D 几何体的展开图
3.(2013 年湖北随州)图 6-2-6 是一个长方体形状包装盒的
表面展开图.折叠制作完成后得到长方体的容积是(包装材料厚度不计)()DA.40×40×70
B. 70×70×80
C. 80×80×40D. 40×70×80图 6-2-6 4.(2013 年四川自贡)如图 6-2-7,将一张边长为 3 的正方
形纸片按虚线裁剪后,恰好围成一个底面是正三角形的棱柱,)A这个棱柱的侧面积为(
A.9-3
B.9C.9-5
2D.9-3
2图 6-2-7 投影
5.(2013 年四川达州)图 6-2-8 是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是()(1)(2)(3)(4)图 6-2-8A.(3)(1)(4)(2)
C.(3)(4)(1)(2)B.(3)(2)(1)(4)
D.(2)(4)(1)(3) 解析:观察四幅图根据影子的方向可知,(3)与(4)是建筑物
在上午时的影子,(1)与(2)是建筑物在下午时的影子,再根据影
子的长短可知 (3)早于(4) , (1)早于(2) , 整个先后顺序为
(3)(4)(1)(2).答案:C 6.(2013 年山东济宁)如图 6-2-9,放映幻灯时,通过光源,
把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为
20 cm,到屏幕的距离为 60 cm,且幻灯片中图形的高度为 6 cm,则屏幕上图形的高度为________cm.
图 6-2-9
图4118 名师点评:与中心投影有关的试题,主要涉及两个方面:
一是根据影子确定光源;二是根据相似的知识求影子的长.与
平行投影有关的试题,关键是紧扣光线平行.1.(2013 年广东湛江)图 6-2-10 是由 6 个大小相同的正方体组成的几何体,它的左视图是()A图 6-2-10ABCD2.(2013 年广东茂名) 如图 6-2-11,由两个相同的正方体)D和一个圆锥体组成一个立体图形,其俯视图是(
图 6-2-11ABCD3.(2012 年广东肇庆)图 6-2-12 是某几何体的三视图,则该几何体是()AA.圆锥
C.三棱柱 B.圆柱
D.三棱锥
图 6-2-12 4.(2012 年广东梅州)春蕾数学兴趣小组用一块正方形木板
在阳光下做投影实验,这块正方形木板在地面上形成的投影可
能是______________(写出符合题意的两个图形即可).
5.(2011 年广东广州)由5个棱长为1的正方体组成图 6-2-13所示的几何体.正方形、菱形522 (1)该几何体的体积是_____(立方单位),表面积是_____(平
方单位);
(2)画出该几何体的主视图和左视图.答案:略图 6-2-13 6.(2013 年广东深圳)如图 6-2-14,该小组发现 8 米高的旗
杆 DE 的影子 EF 落在了包含一圆弧型小桥在内的路上,于是他
们开展了测算小桥所在圆的半径的活动.小刚身高 1.6 米,测
得其影长为 2.4 米,同时测得 EG 的长为 3 米,HF 的长为 1 米,
测得拱高(弧 GH 的中点到弦 GH 的距离,即 MN 的长)为 2 米,
求小桥所在圆的半径.图 6-2-14=解:∵小刚身高 1.6 米,测得其影长为 2.4 米,由相似得DE 1.6
EF 2.4,解得 EF=12.∵EG=3,HF=1,∴GH=EF-EG-HF=8.
1
2
设半径 OG=R,则 OM=R-2.
在 Rt△OMG 中,由勾股定理,得
OM2+MG2=OG2.
即(R-2)2+42=R2,解得 R=5.
因此小桥所在的半径为 5 米.由垂径定理,得GM=—GH=4,又MN=2,
同课章节目录
