2014年中考总复习提能训练课件第六章 第4讲图形的相似
文档属性
| 名称 | 2014年中考总复习提能训练课件第六章 第4讲图形的相似 |

|
|
| 格式 | zip | ||
| 文件大小 | 478.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 12:47:10 | ||
图片预览








文档简介
课件29张PPT。第4讲图形的相似 1.了解比例的基本性质,了解线段的比、成比例线段,通
过建筑、艺术上的实例了解黄金分割.
2.知道相似多边形的对应角相等、对应边成比例、面积的
比等于对应边比的平方.
3.了解两个三角形相似的概念,两个三角形相似的条件.
4.了解图形的位似,能够利用位似将一个图形放大或缩小.考点1比例线段及黄金分割1.在四条线段 a,b,c,d 中,如果 a 与 b 的比等于c 与d
a c
b d简称__________.成比例线段比例线段的比,即—=—,那么这四条线段a,b,c,d叫做___________, ______________________.ad=bc 3.黄金分割.
(1)定义:点 C 把线段 AB 分成两条线段 AC 和 BC,如果
____________,那么线段 AB 被点 C 黄金分割.其中点 C 叫做
线段 AB 的____________,AC 与 AB 的比叫做黄金比.(2)黄金比的比值为,约为 0.618.黄金分割点考点 2相似图形的性质与判定1.相似三角形的定义.相等成比例如果两个三角形的对应角________,对应边____________,那么这两个三角形叫做相似三角形.相等成比例2.相似多边形(三角形)的性质.相似比的平方(1)对应角_______,对应边__________.
(2)周长之比等于_______,面积之比等于______________.
(3)相似三角形对应高的比、对应角平分线的比和对应中线的比等于________.相似比相似比3.相似三角形的判定.两角对应相等 (1)__________________的两个三角形相似.
(2)____________________________的两个三角形相似.
(3)____________________的两个三角形相似.
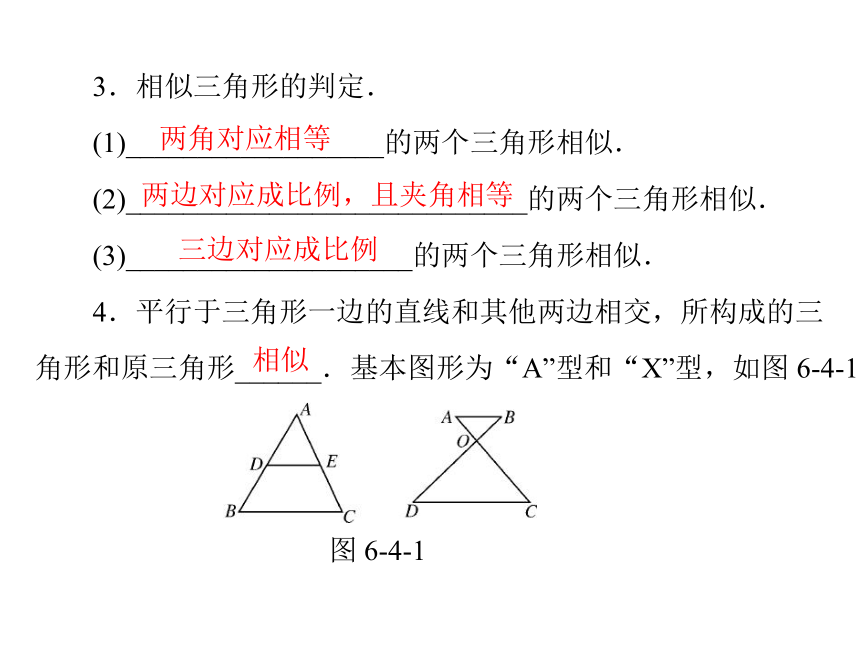
4.平行于三角形一边的直线和其他两边相交,所构成的三
角形和原三角形______.基本图形为“A”型和“X”型,如图 6-4-1.
图 6-4-1两边对应成比例,且夹角相等三边对应成比例相似考点 3位似图形 1.概念:如果两个多边形不仅________,而且对应顶点的
连线相交于__________,这样的图形叫做位似图形,这个点叫做____________.相似一点位似中心位似比 2.性质:位似图形上任意一对对应点到位似中心的距离之
比等于__________.
【学有奇招】
1.深刻理解并掌握“平行截比例”“平行截相似”“比例
出平行”等平行与相似的关系.
2.增强识图能力,能够从已知图形中找出相似三角形,从
中列出所需比例式. 1.在上科学课时,老师让同学利用手中的放大镜对蜗牛进
行观察,同学们在放大镜中看到蜗牛与实际的蜗牛属于什么变换(B.平移变换
D.对称变换A.3
2B.2
3C.3
5D.5
3A )
A.相似变换
C.旋转变换C3.若一个三角形的各边长扩大为原来的 5 倍,则此三角形的周长扩大为原来的________倍.530 4.高 6 m 的旗杆在水平地面上的影子长 4 m,同一时刻附
近有一建筑物的影子长 20 m,则该建筑物的高为_______m.
5.在△ABC 中,D,E分别是边AB 与AC的中点,BC=4,
下面四个结论:①DE=2;②△ADE∽△ABC;③△ADE 的面
积与△ABC 的面积之比为 1∶4;④△ADE 的周长与△ABC 的
周长之比为 1∶4.其中正确的有_____________(只填序号).
①②③相似三角形的判定图 6-4-2 例题:(2013 年湖南益阳)如图 6-4-2,在△ABC 中,AB=
AC,BD=CD,CE⊥AB 于 E.
求证:△ABD∽△CBE.
思路分析:要判断两三角形相似,
由图形可知∠B 是公共角,可再找到一组角相等.
证明:在△ABC 中,AB=AC,BD=CD,∴AD⊥BC.
∵CE⊥AB,∴∠ADB=∠CEB=90°,
又∠B=∠B,∴ △ABD∽△CBE.【试题精选】 1.(2013 年四川南充)如图 6-4-3,在等腰梯形 ABCD 中,
AD∥BC,AD=3,BC=7,∠B=60°,P 为BC边上一点(不与
B,C 重合),过点 P 作∠APE=∠B,PE 交CD 于 E.(1)求证:△APB∽△PEC;
(2)若 CE=3,求 BP 的长.图 6-4-3(1)证明:梯形 ABCD 中,AD∥BC,AB=DC,
∴∠B=∠C=60°.
∵∠APC=∠B+∠BAP,
即∠APE+∠EPC=∠B+∠BAP.
∵∠APE=∠B,∴∠BAP=∠EPC.∴△APB∽△PEC.图 54(2)解:如图 54,过点 A 作 AF∥CD 交 BC 于 F.
则四边形 ADCF 为平行四边形,△ABF 为等边三角形.
∴CF=AD=3,AB=BF=7-3=4.=∴—=∵△APB∽△PEC,∴BP AB
.
EC PC设 BP=x,则 PC=7-x,又 EC=3, AB=4,x
3 4
7-x.整理,得 x2-7x+12=0.解得 x1=3,x2=4.经检验, x1=3,x2=4 是所列方程的根. ∴BP 的长为 3 或 4.
名师点评:相似的判定方法可类比全等三角形的判定方法,
找对应边(角)时应遵循一定的对应原则,如长(大)对长(大),短
(小)对短(小),或找相等的角(边)帮助确定.相似三角形的性质及综合应用 例题:(2013 年福建莆田)定义:如图 6-4-4(1),点 C 在线
段 AB 上,若满足 AC2=BC·AB,则称点 C 为线段 AB 的黄金分
割点.如图 6-4-4(2),在△ABC 中,AB=AC=1,∠A=36°,
BD 平分∠ABC 交 AC 于点 D.(1)求证:点 D 是线段 AC的黄金分割点;(2)求出线段 AD 的长.图 6-4-4 思路分析:先证两三角形相似,借助相似三角形的对应边成
比例构建关系式,进而借助黄金分割点的定义进行判断与计算.
(1)证明:∵∠A=36°,AB=AC,∴∠ABC=∠C=72°.
又∵BD 平分∠ABC,∴∠DBC=∠ABD=36°.
在△ABC 与△BDC 中,∠A=∠DBC,∠C=∠C,【试题精选】
2.(2013 年湖南湘西)如图 6-4-5,在?ABCD 中,E 是 AD
边上的中点,连接 BE,并延长 BE 交 CD 延长线于点 F,则△EDF 与△BCF 的周长之比是()A图 6-4-5A.1∶2B.1∶3C.1∶4D.1∶5 3. (2013 年甘肃)如图 6-4-6,路灯距离地面 8 米,身高 1.6
米的小明站在距离灯的底部(点 O)20 米的 A 处,则小明的影子
AM 长__________米. 5图 6-4-6 名师点评:利用相似三角形的性质可以证明有关线段成比
例、角相等,也可计算三角形中边的长度或角的大小.关键是
要注意相似中的对应边的确认及性质的综合运用,尤其在运用
相似图形的面积比等于相似比的平方时,不要漏了“平方”. 图形的位似
4.(2013 年湖北孝感)在平面直角坐标系中,已知点 E(- 4,2),
1
2 △EFO 缩小,则点 E 的对应点 E′的坐标是()DA.(-2,1)
B.(-8,4)
C.(-8,4)或(8,-4)
D.(-2,1)或(2,-1) F(-2,-2),以原点O为位似中心,相似比为—,把=—,若△AEF 的面积为 2,5.(2013 年四川眉山)如图 6-4-7,在△ABC 中,E,F 分别是 AB,AC 上的两点,且AE
EB=AF
FC1
2则四边形 EBCF 的面积为________.16
名师点评:位似图形一定是相似图形,但相似图形不一定
是位似图形,位似图形是相似图形的特例.图 6-4-7 1.(2011 年广东肇庆)如图6-4-8,已知直线 a∥b∥c,直线
m,n 与 a,b,c 分别交于点 A,C,E,B,D,F,AC=4,CE=6,BD=3,则 BF=(B )
图 6-4-8A.7B.7.5C.8D.8.5 2.(2011 年广东广州)如图 6-4-9,以点 O 为位似中心,将
五边形 ABCDE 放大后得到五边形 A′B′C′D′E′,已知
OA=10 cm,OA′=20 cm,则五边形 ABCDE 的周长与五边形A′B′C′D′E′的周长的比值是_______.
图 6-4-9 3.(2010年广东茂名)如图6-4-10,已知△OAB 与△OA ′B′
是相似比为 1∶2 的位似图形,点 O 是位似中心,若△OAB 内
的一点 P(x,y)与△OA′B′内的一点P′是一对对应点,则点P′的坐标是_____________.
图 6-4-10(-2x,-2y) 4.(2013 年广东佛山)如图 6-4-11,网格图中每个方格都是
边长为 1 的正方形.若 A,B,C,D,E,F 都是格点,试说明
△ABC∽△DEF.
图 6-4-11 5.(2012 年广东梅州)如图 6-4-12,AC 是⊙O 的直径,弦
BD 交 AC 于点 E.
(1)求证:△ADE∽△BCE;图 6-4-12(2)如果 AD2=AE·AC,求证:CD=CB.
证明: (1)∵ = ,∴∠A=∠B.
又∵∠CEB=∠AED,∴△ADE∽△BCE.(2)由 AD2=AE·AC,得AE
AD=AD
.
AC又∵∠A=∠A,∴ △ADE∽△ACD.∴∠AED=∠ADC.
又∵AC是⊙O的直径,∴∠ADC=90°,即有∠AED=90°.
∴直径 AC⊥BD.∴CD=CB. 6.(2012 年广东肇庆)如图 6-4-13,在△ABC 中,AB=AC,
以 AB 为直径的⊙O 交 AC 于点 E,交 BC 于点 D,连接 BE,交
AD 于点 P.求证:(1)D 是 BC 的中点;
(2)△BEC∽△ADC;
(3)AB·CE=2DP·AD.图 6-4-13=,则 2BD2=AC·CE.①证明:(1)∵AB 是直径,∴∠ADB=90°,即 AD⊥BC.
又∵AB=AC,∴D 是 BC 的中点.
(2)在△BEC 与△ADC 中,
∵∠C=∠C,∠CAD=∠CBE,
∴△BEC∽△ADC.(3)∵△BEC∽△ADC,∴AC BC
.
CD CE又∵D 是 BC 的中点, ∴2BD=2CD=BC.∴AC
BD=2BD
CE=,则 BD2=PD·AD.②在△BPD 与△ABD 中,有∠BDP=∠BDA,
又∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD.
又∵∠CAD=∠CBE,∴∠DBP=∠BAD.
∴△BPD∽△ABD.∴BD AD
PD BD∴由①、②,得 AC·CE=2BD2=2PD·AD.
∴AB·CE=2DP·AD.
过建筑、艺术上的实例了解黄金分割.
2.知道相似多边形的对应角相等、对应边成比例、面积的
比等于对应边比的平方.
3.了解两个三角形相似的概念,两个三角形相似的条件.
4.了解图形的位似,能够利用位似将一个图形放大或缩小.考点1比例线段及黄金分割1.在四条线段 a,b,c,d 中,如果 a 与 b 的比等于c 与d
a c
b d简称__________.成比例线段比例线段的比,即—=—,那么这四条线段a,b,c,d叫做___________, ______________________.ad=bc 3.黄金分割.
(1)定义:点 C 把线段 AB 分成两条线段 AC 和 BC,如果
____________,那么线段 AB 被点 C 黄金分割.其中点 C 叫做
线段 AB 的____________,AC 与 AB 的比叫做黄金比.(2)黄金比的比值为,约为 0.618.黄金分割点考点 2相似图形的性质与判定1.相似三角形的定义.相等成比例如果两个三角形的对应角________,对应边____________,那么这两个三角形叫做相似三角形.相等成比例2.相似多边形(三角形)的性质.相似比的平方(1)对应角_______,对应边__________.
(2)周长之比等于_______,面积之比等于______________.
(3)相似三角形对应高的比、对应角平分线的比和对应中线的比等于________.相似比相似比3.相似三角形的判定.两角对应相等 (1)__________________的两个三角形相似.
(2)____________________________的两个三角形相似.
(3)____________________的两个三角形相似.
4.平行于三角形一边的直线和其他两边相交,所构成的三
角形和原三角形______.基本图形为“A”型和“X”型,如图 6-4-1.
图 6-4-1两边对应成比例,且夹角相等三边对应成比例相似考点 3位似图形 1.概念:如果两个多边形不仅________,而且对应顶点的
连线相交于__________,这样的图形叫做位似图形,这个点叫做____________.相似一点位似中心位似比 2.性质:位似图形上任意一对对应点到位似中心的距离之
比等于__________.
【学有奇招】
1.深刻理解并掌握“平行截比例”“平行截相似”“比例
出平行”等平行与相似的关系.
2.增强识图能力,能够从已知图形中找出相似三角形,从
中列出所需比例式. 1.在上科学课时,老师让同学利用手中的放大镜对蜗牛进
行观察,同学们在放大镜中看到蜗牛与实际的蜗牛属于什么变换(B.平移变换
D.对称变换A.3
2B.2
3C.3
5D.5
3A )
A.相似变换
C.旋转变换C3.若一个三角形的各边长扩大为原来的 5 倍,则此三角形的周长扩大为原来的________倍.530 4.高 6 m 的旗杆在水平地面上的影子长 4 m,同一时刻附
近有一建筑物的影子长 20 m,则该建筑物的高为_______m.
5.在△ABC 中,D,E分别是边AB 与AC的中点,BC=4,
下面四个结论:①DE=2;②△ADE∽△ABC;③△ADE 的面
积与△ABC 的面积之比为 1∶4;④△ADE 的周长与△ABC 的
周长之比为 1∶4.其中正确的有_____________(只填序号).
①②③相似三角形的判定图 6-4-2 例题:(2013 年湖南益阳)如图 6-4-2,在△ABC 中,AB=
AC,BD=CD,CE⊥AB 于 E.
求证:△ABD∽△CBE.
思路分析:要判断两三角形相似,
由图形可知∠B 是公共角,可再找到一组角相等.
证明:在△ABC 中,AB=AC,BD=CD,∴AD⊥BC.
∵CE⊥AB,∴∠ADB=∠CEB=90°,
又∠B=∠B,∴ △ABD∽△CBE.【试题精选】 1.(2013 年四川南充)如图 6-4-3,在等腰梯形 ABCD 中,
AD∥BC,AD=3,BC=7,∠B=60°,P 为BC边上一点(不与
B,C 重合),过点 P 作∠APE=∠B,PE 交CD 于 E.(1)求证:△APB∽△PEC;
(2)若 CE=3,求 BP 的长.图 6-4-3(1)证明:梯形 ABCD 中,AD∥BC,AB=DC,
∴∠B=∠C=60°.
∵∠APC=∠B+∠BAP,
即∠APE+∠EPC=∠B+∠BAP.
∵∠APE=∠B,∴∠BAP=∠EPC.∴△APB∽△PEC.图 54(2)解:如图 54,过点 A 作 AF∥CD 交 BC 于 F.
则四边形 ADCF 为平行四边形,△ABF 为等边三角形.
∴CF=AD=3,AB=BF=7-3=4.=∴—=∵△APB∽△PEC,∴BP AB
.
EC PC设 BP=x,则 PC=7-x,又 EC=3, AB=4,x
3 4
7-x.整理,得 x2-7x+12=0.解得 x1=3,x2=4.经检验, x1=3,x2=4 是所列方程的根. ∴BP 的长为 3 或 4.
名师点评:相似的判定方法可类比全等三角形的判定方法,
找对应边(角)时应遵循一定的对应原则,如长(大)对长(大),短
(小)对短(小),或找相等的角(边)帮助确定.相似三角形的性质及综合应用 例题:(2013 年福建莆田)定义:如图 6-4-4(1),点 C 在线
段 AB 上,若满足 AC2=BC·AB,则称点 C 为线段 AB 的黄金分
割点.如图 6-4-4(2),在△ABC 中,AB=AC=1,∠A=36°,
BD 平分∠ABC 交 AC 于点 D.(1)求证:点 D 是线段 AC的黄金分割点;(2)求出线段 AD 的长.图 6-4-4 思路分析:先证两三角形相似,借助相似三角形的对应边成
比例构建关系式,进而借助黄金分割点的定义进行判断与计算.
(1)证明:∵∠A=36°,AB=AC,∴∠ABC=∠C=72°.
又∵BD 平分∠ABC,∴∠DBC=∠ABD=36°.
在△ABC 与△BDC 中,∠A=∠DBC,∠C=∠C,【试题精选】
2.(2013 年湖南湘西)如图 6-4-5,在?ABCD 中,E 是 AD
边上的中点,连接 BE,并延长 BE 交 CD 延长线于点 F,则△EDF 与△BCF 的周长之比是()A图 6-4-5A.1∶2B.1∶3C.1∶4D.1∶5 3. (2013 年甘肃)如图 6-4-6,路灯距离地面 8 米,身高 1.6
米的小明站在距离灯的底部(点 O)20 米的 A 处,则小明的影子
AM 长__________米. 5图 6-4-6 名师点评:利用相似三角形的性质可以证明有关线段成比
例、角相等,也可计算三角形中边的长度或角的大小.关键是
要注意相似中的对应边的确认及性质的综合运用,尤其在运用
相似图形的面积比等于相似比的平方时,不要漏了“平方”. 图形的位似
4.(2013 年湖北孝感)在平面直角坐标系中,已知点 E(- 4,2),
1
2 △EFO 缩小,则点 E 的对应点 E′的坐标是()DA.(-2,1)
B.(-8,4)
C.(-8,4)或(8,-4)
D.(-2,1)或(2,-1) F(-2,-2),以原点O为位似中心,相似比为—,把=—,若△AEF 的面积为 2,5.(2013 年四川眉山)如图 6-4-7,在△ABC 中,E,F 分别是 AB,AC 上的两点,且AE
EB=AF
FC1
2则四边形 EBCF 的面积为________.16
名师点评:位似图形一定是相似图形,但相似图形不一定
是位似图形,位似图形是相似图形的特例.图 6-4-7 1.(2011 年广东肇庆)如图6-4-8,已知直线 a∥b∥c,直线
m,n 与 a,b,c 分别交于点 A,C,E,B,D,F,AC=4,CE=6,BD=3,则 BF=(B )
图 6-4-8A.7B.7.5C.8D.8.5 2.(2011 年广东广州)如图 6-4-9,以点 O 为位似中心,将
五边形 ABCDE 放大后得到五边形 A′B′C′D′E′,已知
OA=10 cm,OA′=20 cm,则五边形 ABCDE 的周长与五边形A′B′C′D′E′的周长的比值是_______.
图 6-4-9 3.(2010年广东茂名)如图6-4-10,已知△OAB 与△OA ′B′
是相似比为 1∶2 的位似图形,点 O 是位似中心,若△OAB 内
的一点 P(x,y)与△OA′B′内的一点P′是一对对应点,则点P′的坐标是_____________.
图 6-4-10(-2x,-2y) 4.(2013 年广东佛山)如图 6-4-11,网格图中每个方格都是
边长为 1 的正方形.若 A,B,C,D,E,F 都是格点,试说明
△ABC∽△DEF.
图 6-4-11 5.(2012 年广东梅州)如图 6-4-12,AC 是⊙O 的直径,弦
BD 交 AC 于点 E.
(1)求证:△ADE∽△BCE;图 6-4-12(2)如果 AD2=AE·AC,求证:CD=CB.
证明: (1)∵ = ,∴∠A=∠B.
又∵∠CEB=∠AED,∴△ADE∽△BCE.(2)由 AD2=AE·AC,得AE
AD=AD
.
AC又∵∠A=∠A,∴ △ADE∽△ACD.∴∠AED=∠ADC.
又∵AC是⊙O的直径,∴∠ADC=90°,即有∠AED=90°.
∴直径 AC⊥BD.∴CD=CB. 6.(2012 年广东肇庆)如图 6-4-13,在△ABC 中,AB=AC,
以 AB 为直径的⊙O 交 AC 于点 E,交 BC 于点 D,连接 BE,交
AD 于点 P.求证:(1)D 是 BC 的中点;
(2)△BEC∽△ADC;
(3)AB·CE=2DP·AD.图 6-4-13=,则 2BD2=AC·CE.①证明:(1)∵AB 是直径,∴∠ADB=90°,即 AD⊥BC.
又∵AB=AC,∴D 是 BC 的中点.
(2)在△BEC 与△ADC 中,
∵∠C=∠C,∠CAD=∠CBE,
∴△BEC∽△ADC.(3)∵△BEC∽△ADC,∴AC BC
.
CD CE又∵D 是 BC 的中点, ∴2BD=2CD=BC.∴AC
BD=2BD
CE=,则 BD2=PD·AD.②在△BPD 与△ABD 中,有∠BDP=∠BDA,
又∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD.
又∵∠CAD=∠CBE,∴∠DBP=∠BAD.
∴△BPD∽△ABD.∴BD AD
PD BD∴由①、②,得 AC·CE=2BD2=2PD·AD.
∴AB·CE=2DP·AD.
同课章节目录
