2014年中考总复习提能训练课件第三章 第3讲反比例函数
文档属性
| 名称 | 2014年中考总复习提能训练课件第三章 第3讲反比例函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 637.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 00:00:00 | ||
图片预览









文档简介
课件34张PPT。第3讲反比例函数 1.结合具体情境体会反比例函数的意义,能根据已知条件
确定反比例函数表达式.
2.能画出反比例函数的图象,根据图象和解析表达式 y=k
x(k≠0)探索并理解其性质(k>0 或 k<0 时,图象的变化).
3.能用反比例函数解决某些实际问题.考点1反比例函数的图象和性质1.反比例函数的概念. 定义:形如____________的函数称为反比例函数,其中 x 是
自变量,y 是函数,自变量的取值范围是不等于 0 的一切实数.
注意:另外两种形式为y=kx-1 (k≠0)、k=xy(k≠0).2.反比例函数的图象和性质.双曲线原点 (1)图象特征:
①由两条曲线组成,叫做__________;
②图象的两个分支都无限接近 x 轴和 y 轴,但都不会与 x
轴和 y 轴相交;
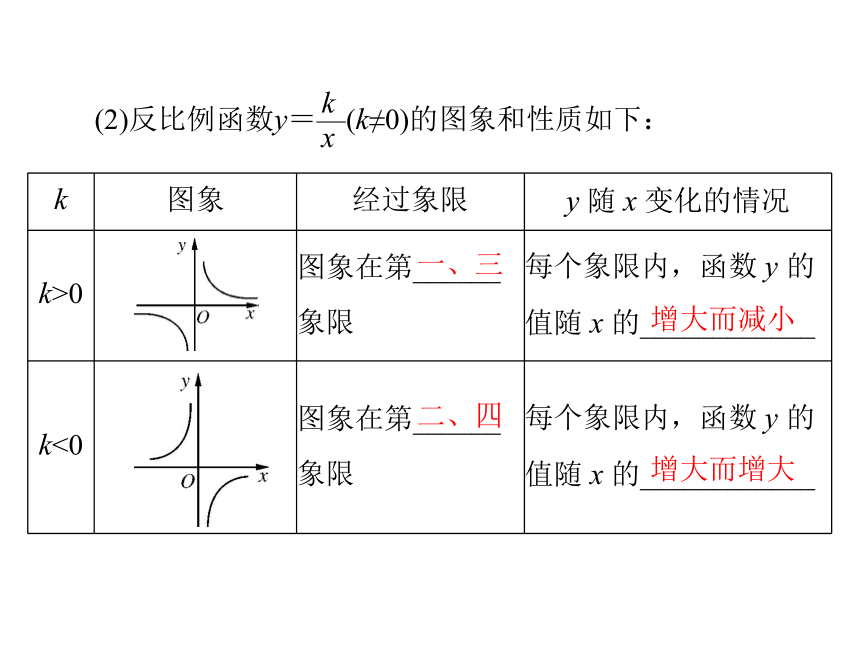
③图象是以______为对称中心的中心对称图形.(2)反比例函数y=—(k≠0)的图象和性质如下:k
x一、三增大而减小二、四增大而增大考点2确定反比例函数的表达式与确定一次函数表达式的方法一样,即用待定系数法.考点3k 的几何意义|xy|=|k| 如图 3-3-1,过双曲线上任一点 P 作 x 轴、y 轴的垂线 PM、
PN,所得矩形 PMON 的面积为____________.
图 3-3-1【学有奇招】 1. 求反比例函数的解析式一般用待定系数法,充分利用反
比例函数定义解决反比例函数与一次函数的综合应用问题,通
过专题复习与训练加深对具体问题的分析、理解,得出解决问
题的方法和途径. 2.口决:反比例函数双曲线,待定只需一个点,正 k 落在
一三限,x 增大 y 在减,负 k 落在二四限,x 减小 y 才减,图象
上面任意点,矩形面积都不变.1.如果函数 y=x2m-1 为反比例函数,那么 m 的值是()A.-1B. 0C.1
2D.1Bk
x函数的图象应在()AA.第一、三象限
C.第二、四象限B.第一、二象限
D.第三、四象限2.如果反比例函数y=—的图象经过点(-3,-4),那么此 k
x图象大致是()D2
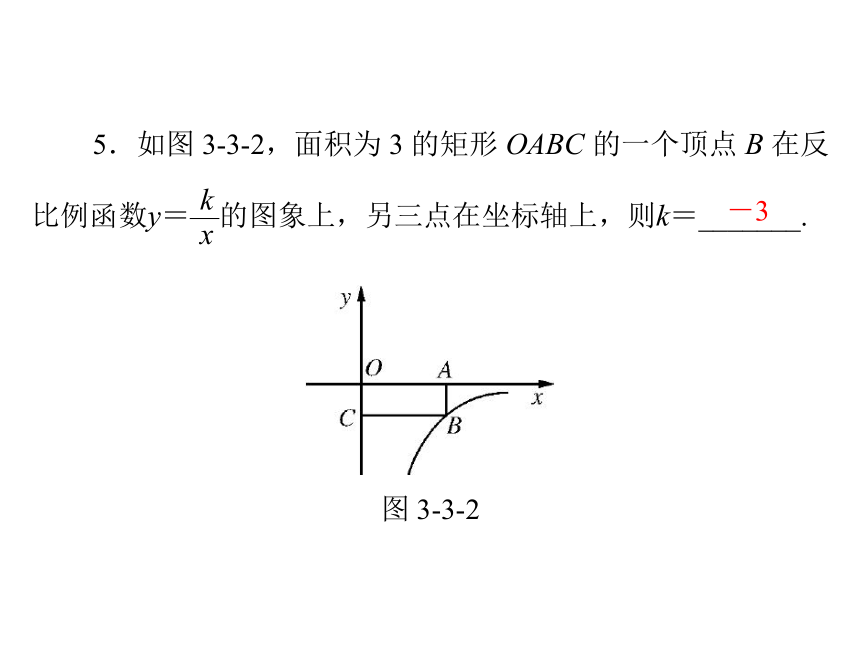
x大小关系为__________.y1x图 3-3-2反比例函数的图象和性质1.(2013年福建厦门)已知反比例函数 y=m-1
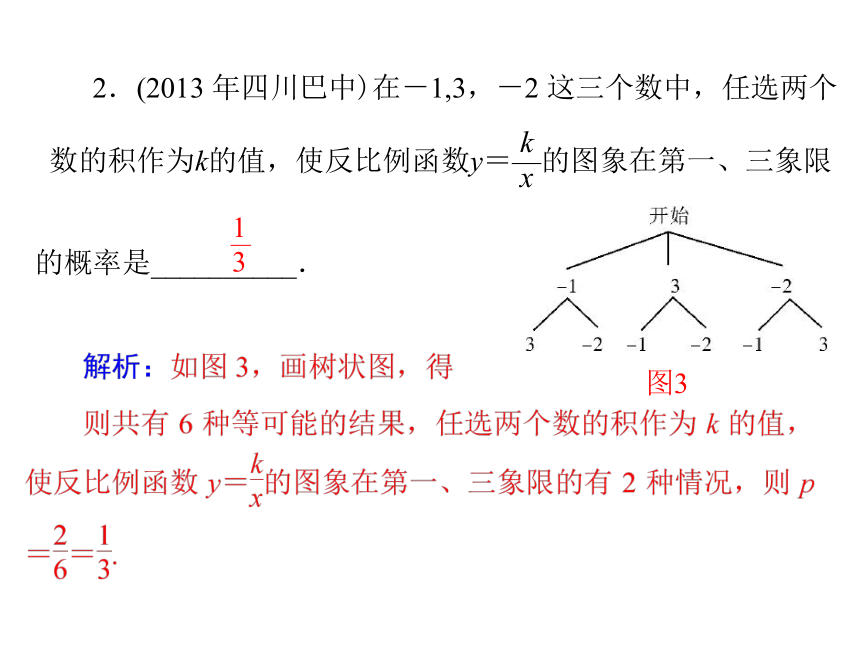
x的图象的一支位于第一象限,则常数 m 的取值范围是______.m>12.(2013 年四川巴中)在-1,3,-2 这三个数中,任选两个
k
x的概率是__________.数的积作为k的值,使反比例函数y=—的图象在第一、三象限 图3 3.(2013 年湖南株洲)已知点 A(1,y1),B(2,y2),C(-3,
6
x()DA.y3<y1<y2
C.y2<y1<y3B.y1<y2<y3
D.y3<y2<y1 名师点评:利用反比例函数的图象解题时,关键是先根据
k 的值确定其图象分布在哪几个象限,弄清楚y 随x 的变化情况,
才能有效地解决问题.y3)都在反比例函数y=—的图象上,则y1,y2,y3的大小关系是 确定反比例函数的表达式
k
x(1,- 2),则 k 的值为________.-24.(2013年江苏徐州)反比例函数y=—的图象经过点(2)直接写出不等式 ax+b≥— 的解集.(1)求该反比例函数和一次函数的解析式;k
x图 3-3-3 名师点评:用待定系数法求反比例函数的解析式,要充分
利用一次函数与反比例函数的交点,交点即在一次函数的图象
上,又在反比例函数的图象上,分别代入得到方程和方程组即
可得解,难度适中.反比例函数的综合运用轴上任意一点,求△PAB 的面积.
思路分析:先分别求出 A,B 两点的
坐标,得到 AB 的长度,再根据三角形的
面积公式即可得出△PAB 的面积.图3-3-4【试题精选】
6.(2013 年山东泰安)如图 3-3-5,四边形 ABCD 为正方形,
k
x
图象经过点 C,一次函数 y=ax+b 的图象经过点 A,C.
(1)求反比例函数与一次函数的解析式;
(2)点 P 是反比例函数图象上的一点,
△OAP 的面积恰好等于正方形 ABCD 的面积,求点 P 的坐标.图 3-3-5点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=—的 名师点评:反比例函数与一次函数的交点问题,是考试的
一个热点.关键是确定它们一个交点的坐标,然后就可以用待
定系数法求解析式,最后解决问题.1.(2011 年广东茂名)若函数 y=m+2
x的图象在其象限内 y的值随 x 的增大而增大,则 m 的取值范围是()BA.m>-2
C.m>2B.m<-2
D.m<22.(2013 年广东)已知 k1<0 x的图象大致是()Ak
xA(1,2),则 k=________.2 k
x
在第一象限内交于 P,Q 两点,分别过 P,
Q 两点向 x 轴和 y 轴作垂线,已知点 P 的
坐标为(1,3),则图中阴影部分的面积为________.4图 3-3-64.(2012年广东深圳)如图3-3-6,双曲线y=—(k>0)与⊙O 3.(2013年广东湛江)若反比例函数y=—的图象经过点 y=—的图象有一个公共点 A(1,2).5.(2013 年广东佛山)已知正比例函数 y=ax 与反比例函数b
x(1)求这两个函数的表达式;(2)在图 3-3-7 中画出草图,根据图象写出正比例函数值大于反比例函数值
时 x 的取值范围.图 3-3-7把A(1,2)代入y=—得b=1×2=2,所以反比例函数解析式为y=—.解:(1)把 A(1,2)代入 y=ax 得 a=2,
所以正比例函数解析式为 y=2x.b
x2
x(2)如图 4,当-1<x<0 或x>1 时,正比例函数值大于反比
例函数值.OB,函数 y=- —的图象与线段 AB 交于 M 点,且 AM=BM. 6.(2013 年广东珠海)如图3-3-8,在平面直角坐标系 xOy
中,点 A 在 x 轴的负半轴上,点 B 在 y 轴的正半轴上,OA=8
x(1)求点 M 的坐标;(2)求直线 AB 的解析式.图 3-3-8把点M(-a,a)代入函数y=-—中,解得a=2 .解:(1)如图 5,过点 M 作 MC⊥x 轴,MD⊥y 轴,∵AM=BM,∴点 M 为 AB 的中点.∵MC⊥x 轴,MD⊥y 轴,
∴MC∥OB,MD∥OA.∴点 C 和点 D 分别为 OA 与 OB 的中点,
∴MC=MD.则点 M 的坐标可以表示为(-a,a),8
x图5 7.(2013 年广东广州)如图 3-3-9,在平面直角坐标系中,
点 O 为坐标原点,正方形 OABC 的边 OA、OC 分别在 x 轴、y
k
x
象经过线段 BC 的中点 D.
(1)求 k 的值;
(2)若点 P(x,y)在该反比例函
数的图象上运动(不与点 D 重合),
过点 P 作 PR⊥y 轴于点 R,作 PQ⊥BC
所在直线于点 Q,记四边形 CQPR 的面积为 S,求 S 关于 x 的解析式,并写出 x 的取值范围.图 3-3-9轴上,点B的坐标为(2, 2),反比例函数y=—(x>0,k≠0)的图 图 7
确定反比例函数表达式.
2.能画出反比例函数的图象,根据图象和解析表达式 y=k
x(k≠0)探索并理解其性质(k>0 或 k<0 时,图象的变化).
3.能用反比例函数解决某些实际问题.考点1反比例函数的图象和性质1.反比例函数的概念. 定义:形如____________的函数称为反比例函数,其中 x 是
自变量,y 是函数,自变量的取值范围是不等于 0 的一切实数.
注意:另外两种形式为y=kx-1 (k≠0)、k=xy(k≠0).2.反比例函数的图象和性质.双曲线原点 (1)图象特征:
①由两条曲线组成,叫做__________;
②图象的两个分支都无限接近 x 轴和 y 轴,但都不会与 x
轴和 y 轴相交;
③图象是以______为对称中心的中心对称图形.(2)反比例函数y=—(k≠0)的图象和性质如下:k
x一、三增大而减小二、四增大而增大考点2确定反比例函数的表达式与确定一次函数表达式的方法一样,即用待定系数法.考点3k 的几何意义|xy|=|k| 如图 3-3-1,过双曲线上任一点 P 作 x 轴、y 轴的垂线 PM、
PN,所得矩形 PMON 的面积为____________.
图 3-3-1【学有奇招】 1. 求反比例函数的解析式一般用待定系数法,充分利用反
比例函数定义解决反比例函数与一次函数的综合应用问题,通
过专题复习与训练加深对具体问题的分析、理解,得出解决问
题的方法和途径. 2.口决:反比例函数双曲线,待定只需一个点,正 k 落在
一三限,x 增大 y 在减,负 k 落在二四限,x 减小 y 才减,图象
上面任意点,矩形面积都不变.1.如果函数 y=x2m-1 为反比例函数,那么 m 的值是()A.-1B. 0C.1
2D.1Bk
x函数的图象应在()AA.第一、三象限
C.第二、四象限B.第一、二象限
D.第三、四象限2.如果反比例函数y=—的图象经过点(-3,-4),那么此 k
x图象大致是()D2
x大小关系为__________.y1
x的图象的一支位于第一象限,则常数 m 的取值范围是______.m>12.(2013 年四川巴中)在-1,3,-2 这三个数中,任选两个
k
x的概率是__________.数的积作为k的值,使反比例函数y=—的图象在第一、三象限 图3 3.(2013 年湖南株洲)已知点 A(1,y1),B(2,y2),C(-3,
6
x()DA.y3<y1<y2
C.y2<y1<y3B.y1<y2<y3
D.y3<y2<y1 名师点评:利用反比例函数的图象解题时,关键是先根据
k 的值确定其图象分布在哪几个象限,弄清楚y 随x 的变化情况,
才能有效地解决问题.y3)都在反比例函数y=—的图象上,则y1,y2,y3的大小关系是 确定反比例函数的表达式
k
x(1,- 2),则 k 的值为________.-24.(2013年江苏徐州)反比例函数y=—的图象经过点(2)直接写出不等式 ax+b≥— 的解集.(1)求该反比例函数和一次函数的解析式;k
x图 3-3-3 名师点评:用待定系数法求反比例函数的解析式,要充分
利用一次函数与反比例函数的交点,交点即在一次函数的图象
上,又在反比例函数的图象上,分别代入得到方程和方程组即
可得解,难度适中.反比例函数的综合运用轴上任意一点,求△PAB 的面积.
思路分析:先分别求出 A,B 两点的
坐标,得到 AB 的长度,再根据三角形的
面积公式即可得出△PAB 的面积.图3-3-4【试题精选】
6.(2013 年山东泰安)如图 3-3-5,四边形 ABCD 为正方形,
k
x
图象经过点 C,一次函数 y=ax+b 的图象经过点 A,C.
(1)求反比例函数与一次函数的解析式;
(2)点 P 是反比例函数图象上的一点,
△OAP 的面积恰好等于正方形 ABCD 的面积,求点 P 的坐标.图 3-3-5点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=—的 名师点评:反比例函数与一次函数的交点问题,是考试的
一个热点.关键是确定它们一个交点的坐标,然后就可以用待
定系数法求解析式,最后解决问题.1.(2011 年广东茂名)若函数 y=m+2
x的图象在其象限内 y的值随 x 的增大而增大,则 m 的取值范围是()BA.m>-2
C.m>2B.m<-2
D.m<22.(2013 年广东)已知 k1<0
xA(1,2),则 k=________.2 k
x
在第一象限内交于 P,Q 两点,分别过 P,
Q 两点向 x 轴和 y 轴作垂线,已知点 P 的
坐标为(1,3),则图中阴影部分的面积为________.4图 3-3-64.(2012年广东深圳)如图3-3-6,双曲线y=—(k>0)与⊙O 3.(2013年广东湛江)若反比例函数y=—的图象经过点 y=—的图象有一个公共点 A(1,2).5.(2013 年广东佛山)已知正比例函数 y=ax 与反比例函数b
x(1)求这两个函数的表达式;(2)在图 3-3-7 中画出草图,根据图象写出正比例函数值大于反比例函数值
时 x 的取值范围.图 3-3-7把A(1,2)代入y=—得b=1×2=2,所以反比例函数解析式为y=—.解:(1)把 A(1,2)代入 y=ax 得 a=2,
所以正比例函数解析式为 y=2x.b
x2
x(2)如图 4,当-1<x<0 或x>1 时,正比例函数值大于反比
例函数值.OB,函数 y=- —的图象与线段 AB 交于 M 点,且 AM=BM. 6.(2013 年广东珠海)如图3-3-8,在平面直角坐标系 xOy
中,点 A 在 x 轴的负半轴上,点 B 在 y 轴的正半轴上,OA=8
x(1)求点 M 的坐标;(2)求直线 AB 的解析式.图 3-3-8把点M(-a,a)代入函数y=-—中,解得a=2 .解:(1)如图 5,过点 M 作 MC⊥x 轴,MD⊥y 轴,∵AM=BM,∴点 M 为 AB 的中点.∵MC⊥x 轴,MD⊥y 轴,
∴MC∥OB,MD∥OA.∴点 C 和点 D 分别为 OA 与 OB 的中点,
∴MC=MD.则点 M 的坐标可以表示为(-a,a),8
x图5 7.(2013 年广东广州)如图 3-3-9,在平面直角坐标系中,
点 O 为坐标原点,正方形 OABC 的边 OA、OC 分别在 x 轴、y
k
x
象经过线段 BC 的中点 D.
(1)求 k 的值;
(2)若点 P(x,y)在该反比例函
数的图象上运动(不与点 D 重合),
过点 P 作 PR⊥y 轴于点 R,作 PQ⊥BC
所在直线于点 Q,记四边形 CQPR 的面积为 S,求 S 关于 x 的解析式,并写出 x 的取值范围.图 3-3-9轴上,点B的坐标为(2, 2),反比例函数y=—(x>0,k≠0)的图 图 7
同课章节目录
