2014年中考总复习提能训练课件第四章 第2讲第1课时三角形
文档属性
| 名称 | 2014年中考总复习提能训练课件第四章 第2讲第1课时三角形 |

|
|
| 格式 | zip | ||
| 文件大小 | 335.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 12:41:19 | ||
图片预览







文档简介
课件25张PPT。第2讲 三角形第 1 课时三角形 1.了解三角形有关概念(内角、外角、中线、高、角平分
线),会画出任意三角形的角平分线、中线和高,了解三角形的
稳定性.
2.掌握三角形中位线的性质.
3.了解全等三角形的概念,掌握两个三角形全等的条件.考点1三角形及其边角关系1.边与边的关系.大于小于 三角形任意两边之和______第三边,任意两边之差_______
第三边.2.角与角的关系.180°360°等于(1)三角形的内角和等于_______,外角和等于_______.
(2)三角形的一个外角______与它不相邻的两个内角和. 3.三角形中的重要线段.
三角形的角平分线、三角形的中线、三角形的高、三角形
的中位线.
(1)三角形的中位线:连接三角形两边__________的线段.
(2) 三角形的中位线平行于第三边,并且等于第三边的__________.中点一半考点2三角形的分类1.按角的关系分类.
直角三角形
三角形 斜三角形
2.按边的关系分类.
不等边三角形
三角形 等腰三角形 底和腰不相等的等腰三角形等边三角形锐角三角形
钝角三角形考点3三角形全等的判定与性质1.全等三角形:能完全重合的两个三角形.
2.三角形全等的判定方法.
(1)SSS:三边对应相等的两个三角形全等.
(2)SAS:两边和它们的______对应相等的两个三角形全等.
(3)ASA:两角和它们的_____对应相等的两个三角形全等.
(4)AAS:两角和其中一个角的对边对应相等的两个三角形全等.夹角夹边一条直角边(5)HL:斜边和___________对应相等的两个直角三角形全等.3.全等三角形的性质.
(1)全等三角形的对应边、对应角________.
(2) 全等三角形的对应角平分线、对应中线、对应高线________.相等相等相等相等(3)全等三角形的周长________、面积________.【学有奇招】 1.利用全等三角形解答有关问题的证明思路是:根据已知
条件,得到全等三角形,再得到线段关系或角的关系,其中判
断线段关系分为数量关系和位置关系. 2.三角形全等口诀:全等判定三条件,总得有边方实现.
已知元素图上标,边角关系清晰见;三边对等最易找,两边一
角需夹角,两角一边任意边,角角边或角边角;三角抑或边边
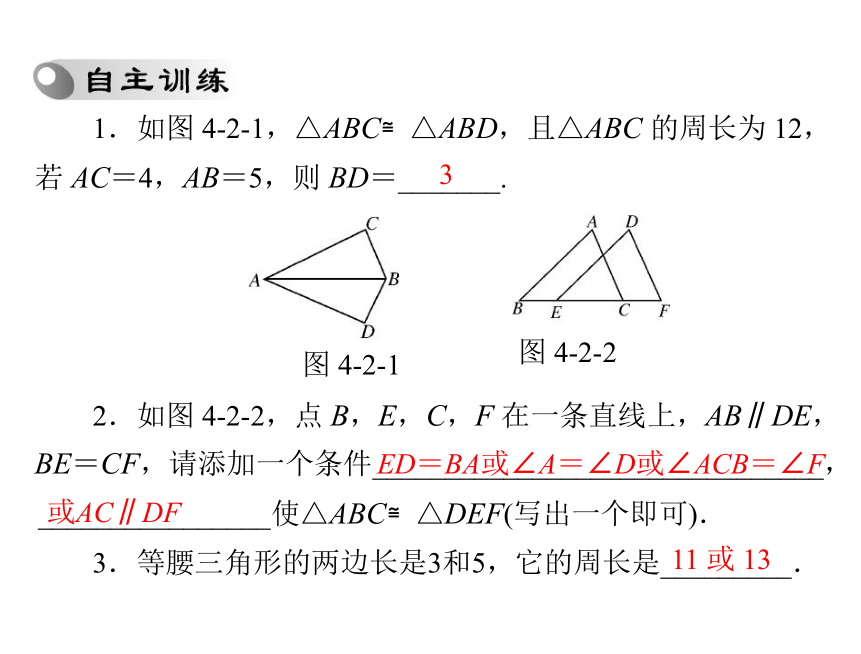
角,不能全等莫推导.1.如图 4-2-1,△ABC≌△ABD,且△ABC 的周长为 12,若 AC=4,AB=5,则 BD=_______.
图 4-2-1
图 4-2-2 2.如图 4-2-2,点 B,E,C,F 在一条直线上,AB∥DE,
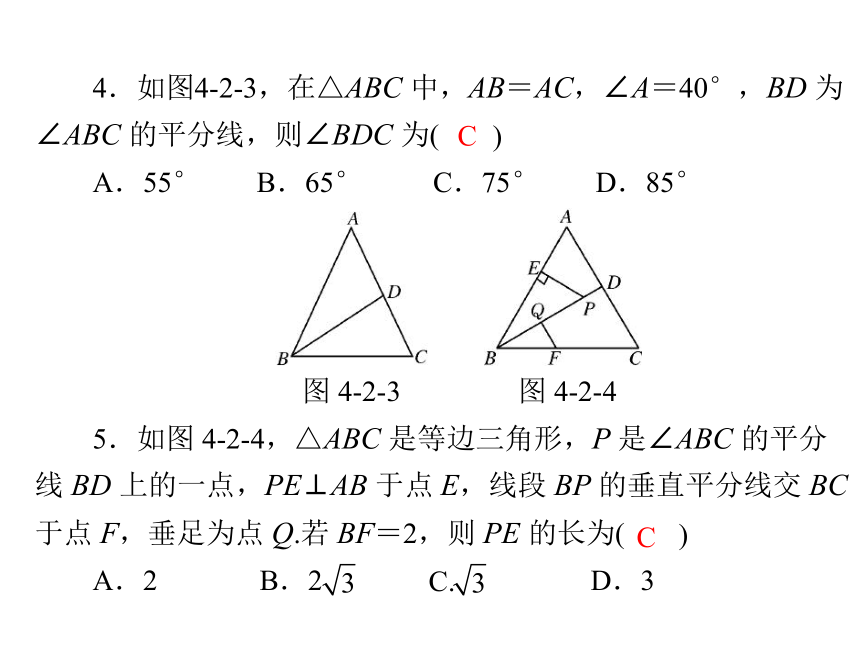
BE=CF,请添加一个条件_______________________________,________________使△ABC≌△DEF(写出一个即可).11 或 133.等腰三角形的两边长是3和5,它的周长是_________.3ED=BA或∠A=∠D或∠ACB=∠F或AC∥DF4.如图4-2-3,在△ABC 中,AB=AC,∠A=40°,BD 为∠ABC 的平分线,则∠BDC 为()CA.55°B.65°C.75°D.85°图 4-2-3图 4-2-4 5.如图 4-2-4,△ABC 是等边三角形,P 是∠ABC 的平分
线 BD 上的一点,PE⊥AB 于点 E,线段 BP 的垂直平分线交 BC于点 F,垂足为点 Q.若 BF=2,则 PE 的长为()CA.2B.2C. D.3 三角形有关边、面积的计算
例题:(2013 年江苏南通)有3 cm、6 cm、8 cm、9 cm 的四
条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为()A.1 个B.2 个C.3 个D.4 个 解析:根据三角形三边关系定理可知,能组成的三角形的
情况是:①3 cm、6 cm、8 cm;②3 cm、8 cm、9 cm;③6 cm、
8 cm、9 cm 三种情况.故选 C.
答案:C【试题精选】
1.(2013 年湖南长沙)如果一个三角形两边的长分别是2 和4,则第三边长可能是()BA.2B.4C.6D.8 名师点评:三角形三边关系主要体现在:一是判断三边能
否构成三角形;二是已知三角形两边的长,确定第三边的取值
范围;三是证明线段间的不等关系.在计算三角形的周长时,
注意不能盲目地将三边长相加起来,而应养成检验三边长能否
组成三角形的好习惯,把不符合题意的舍去. 三角形有关角的计算
2.(2013 年湖北鄂州)一副三角板有两个直角三角形,如图4-2-5 叠放在一起,则∠α的度数是()AA.165°B.120° C.150°D.135° 图 4-2-5
提示:∠α 可看成是△ DPB 的一外角. 3.(2013 年四川乐山)如图 4-2-6,
在四边形 ABCD 中,∠A=45°.直线 l
与边 AB,AD 分别相交于点 M,N,则∠1+∠2=________.225°图 4-2-6 解析:由三角形的外角和定理,得∠1=∠A+∠AMN,
∠2=∠A+∠ANM,又∵∠A=45°,∴∠AMN+∠ANM=
135°, ∴∠1+∠2=2∠A+135°=225°.
名师点评:计算角的度数,往往转化与利用三角形的内角
和或外角,有时还要灵活应用多边形的内角和定理.全等三角形的性质与判定例题:(2013 年湖北十堰)如图 4-2-7,点 D,E 在△ABC 的边 BC 上,AB=AC,BD=CE.求证:AD=AE.图 4-2-7 思路分析:利用等腰三角形的性质“等边对等角”及条件,
借助“边角边”易证△ABD≌△ACE,根据全等三角形的性质
得 AD=AE.【试题精选】 4.(2013 年湖北仙桃)如图 4-2-8,已知△ABC≌△ADE,
AB 与 ED 交于点 M,BC 与 ED,AD 分别交于点 F,N.请写出
图中两对全等三角形(△ABC≌△ADE 除外),并选择其中的一
对加以证明.图 4-2-8解:AEM≌△ACN,△BMF≌△DNF,△ABN≌△ADM(三对任写两对即可).①选择△AEM≌△ACN,理由如下:
∵△ADE≌△ABC,∴AE=AC,∠E=∠C,∠EAD=∠CAB.
∴∠EAM=∠CAN.∴△AEM≌△ACN(ASA)②选择△ABN≌△ADM,理由如下:∵△ADE≌△ABC,∴AB=AD,∠B=∠D.
∵∠BAN=∠DAM,∴△ABN≌△ADM(ASA).③选择△BMF≌△DNF,理由如下:
∵△ABN≌△ADM(由②可证),
∴AM=AN.∴BM=DN.∵∠B=∠D,∠BFM=∠DFN,
∴△BMF≌△DNF(AAS). 名师点评:证明有关线段或角相等,通常证三角形全等.
三角形全等的证明方法有 SAS,ASA,AAS,SSS.直角三角形
还有另外一种“HL”判定方法.1.(2012 年广东)已知三角形两边的长分别是 4 和 10,则此三角形第三边的长可能是()CA.5B.6C.11D.162.(2011 年广东茂名)如图 4-2-9,在△ABC 中,D,E 分别是 AB,AC 的中点,若 DE=5,则 BC=()A.6B.8C.10D.12图 4-2-9C 3.(2012 年广东梅州)如图 4-2-10,在折纸活动中,小明制
作了一张△ABC 纸片,点 D,E 分别在边 AB,AC 上,将△ABC
沿着 DE 折叠压平,A 与 A′重合,若∠A=75°,则∠1+∠2=()A图 4-2-10A.150°B.210°C.105°D.75°4.(2013 年广东珠海)如图4-2-11,已知,EC=AC,∠BCE图 4-2-11=∠DCA,∠A=∠E,求证:BC=DC.
证明:∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ACE,
即∠BCA=∠DCE.
∵AC=EC,∠A=∠E,
∴△BCA≌△DCE(ASA).
∴BC=DC. 5.(2013 年广东佛山)课本指出:公认的真命题称为公理,
除了公理外,其他的真命题(如推论、定理等)的正确性都需要
通过推理的方法证实(如图 4-2-12).(1) 叙述三角形全等的判定方法中的推论 AAS;
(2) 证明推论 AAS.要求:叙述推论用文字表达;用图形中的符号表达已知、求证,并证明,证明对各步骤要注明依据.图 4-2-12解:(1)一个三角形的两个角和其中一个角的对边分别相等的两个三角形全等.(2)已知:在△ABC 和△DEF 中,
∠A=∠D,∠B=∠E,BC=EF,
求证:△ABC≌△DEF.证明:因为∠A +∠B +∠C =180° ,∠D +∠E +∠F =180°(三角形内角和定理),又∠A=∠D,∠B=∠E(已知),
所以∠C=∠F(等式的性质).在△ABC 和△DEF 中,∠B=∠E(已知),BC=EF(已知),∠C=∠F(已证),所以△ABC≌△DEF(ASA). 6.(2013年广东茂名)如图 4-2-13,已知:在矩形ABCD 中,
F 是 BC 上的一点,且 AF=BC , DE⊥AF ,垂足是 E,连接
DF.
求证:(1)△ABF≌△DEA;(2) DF 是∠EDC 的平分线.图 4-2-13证明:(1)∵四边形 ABCD 是矩形,
∴∠B=90°,AD=BC,AD∥BC.
∴∠DAE=∠AFB.
∵DE⊥AF, ∴∠DEA=∠B=90°.
∵AF=BC,∴AF=AD ∴. △ ABF≌△DEA.(2)证法一,由(1)知△ABF≌△DEA,∴DE=AB.
∵四边形 ABCD 是矩形,∴∠C=90°,DC=AB.∴DC=DE.∵∠DEA=90°,∴∠C=∠DEF=90°.
∵DF= DF ,∴ △ DCF≌ △ DEF.∴∠EDF=∠CDF.∴DF 是∠EDC 的平分线.
证法二,由(1)知△ABF≌△DEA,∴BF=EA.
∵AF=BC,∴EF=CF.∵∠DEA=90°,∴∠C=∠DEF=90°.
∴DF 是∠EDC 的平分线.
线),会画出任意三角形的角平分线、中线和高,了解三角形的
稳定性.
2.掌握三角形中位线的性质.
3.了解全等三角形的概念,掌握两个三角形全等的条件.考点1三角形及其边角关系1.边与边的关系.大于小于 三角形任意两边之和______第三边,任意两边之差_______
第三边.2.角与角的关系.180°360°等于(1)三角形的内角和等于_______,外角和等于_______.
(2)三角形的一个外角______与它不相邻的两个内角和. 3.三角形中的重要线段.
三角形的角平分线、三角形的中线、三角形的高、三角形
的中位线.
(1)三角形的中位线:连接三角形两边__________的线段.
(2) 三角形的中位线平行于第三边,并且等于第三边的__________.中点一半考点2三角形的分类1.按角的关系分类.
直角三角形
三角形 斜三角形
2.按边的关系分类.
不等边三角形
三角形 等腰三角形 底和腰不相等的等腰三角形等边三角形锐角三角形
钝角三角形考点3三角形全等的判定与性质1.全等三角形:能完全重合的两个三角形.
2.三角形全等的判定方法.
(1)SSS:三边对应相等的两个三角形全等.
(2)SAS:两边和它们的______对应相等的两个三角形全等.
(3)ASA:两角和它们的_____对应相等的两个三角形全等.
(4)AAS:两角和其中一个角的对边对应相等的两个三角形全等.夹角夹边一条直角边(5)HL:斜边和___________对应相等的两个直角三角形全等.3.全等三角形的性质.
(1)全等三角形的对应边、对应角________.
(2) 全等三角形的对应角平分线、对应中线、对应高线________.相等相等相等相等(3)全等三角形的周长________、面积________.【学有奇招】 1.利用全等三角形解答有关问题的证明思路是:根据已知
条件,得到全等三角形,再得到线段关系或角的关系,其中判
断线段关系分为数量关系和位置关系. 2.三角形全等口诀:全等判定三条件,总得有边方实现.
已知元素图上标,边角关系清晰见;三边对等最易找,两边一
角需夹角,两角一边任意边,角角边或角边角;三角抑或边边
角,不能全等莫推导.1.如图 4-2-1,△ABC≌△ABD,且△ABC 的周长为 12,若 AC=4,AB=5,则 BD=_______.
图 4-2-1
图 4-2-2 2.如图 4-2-2,点 B,E,C,F 在一条直线上,AB∥DE,
BE=CF,请添加一个条件_______________________________,________________使△ABC≌△DEF(写出一个即可).11 或 133.等腰三角形的两边长是3和5,它的周长是_________.3ED=BA或∠A=∠D或∠ACB=∠F或AC∥DF4.如图4-2-3,在△ABC 中,AB=AC,∠A=40°,BD 为∠ABC 的平分线,则∠BDC 为()CA.55°B.65°C.75°D.85°图 4-2-3图 4-2-4 5.如图 4-2-4,△ABC 是等边三角形,P 是∠ABC 的平分
线 BD 上的一点,PE⊥AB 于点 E,线段 BP 的垂直平分线交 BC于点 F,垂足为点 Q.若 BF=2,则 PE 的长为()CA.2B.2C. D.3 三角形有关边、面积的计算
例题:(2013 年江苏南通)有3 cm、6 cm、8 cm、9 cm 的四
条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为()A.1 个B.2 个C.3 个D.4 个 解析:根据三角形三边关系定理可知,能组成的三角形的
情况是:①3 cm、6 cm、8 cm;②3 cm、8 cm、9 cm;③6 cm、
8 cm、9 cm 三种情况.故选 C.
答案:C【试题精选】
1.(2013 年湖南长沙)如果一个三角形两边的长分别是2 和4,则第三边长可能是()BA.2B.4C.6D.8 名师点评:三角形三边关系主要体现在:一是判断三边能
否构成三角形;二是已知三角形两边的长,确定第三边的取值
范围;三是证明线段间的不等关系.在计算三角形的周长时,
注意不能盲目地将三边长相加起来,而应养成检验三边长能否
组成三角形的好习惯,把不符合题意的舍去. 三角形有关角的计算
2.(2013 年湖北鄂州)一副三角板有两个直角三角形,如图4-2-5 叠放在一起,则∠α的度数是()AA.165°B.120° C.150°D.135° 图 4-2-5
提示:∠α 可看成是△ DPB 的一外角. 3.(2013 年四川乐山)如图 4-2-6,
在四边形 ABCD 中,∠A=45°.直线 l
与边 AB,AD 分别相交于点 M,N,则∠1+∠2=________.225°图 4-2-6 解析:由三角形的外角和定理,得∠1=∠A+∠AMN,
∠2=∠A+∠ANM,又∵∠A=45°,∴∠AMN+∠ANM=
135°, ∴∠1+∠2=2∠A+135°=225°.
名师点评:计算角的度数,往往转化与利用三角形的内角
和或外角,有时还要灵活应用多边形的内角和定理.全等三角形的性质与判定例题:(2013 年湖北十堰)如图 4-2-7,点 D,E 在△ABC 的边 BC 上,AB=AC,BD=CE.求证:AD=AE.图 4-2-7 思路分析:利用等腰三角形的性质“等边对等角”及条件,
借助“边角边”易证△ABD≌△ACE,根据全等三角形的性质
得 AD=AE.【试题精选】 4.(2013 年湖北仙桃)如图 4-2-8,已知△ABC≌△ADE,
AB 与 ED 交于点 M,BC 与 ED,AD 分别交于点 F,N.请写出
图中两对全等三角形(△ABC≌△ADE 除外),并选择其中的一
对加以证明.图 4-2-8解:AEM≌△ACN,△BMF≌△DNF,△ABN≌△ADM(三对任写两对即可).①选择△AEM≌△ACN,理由如下:
∵△ADE≌△ABC,∴AE=AC,∠E=∠C,∠EAD=∠CAB.
∴∠EAM=∠CAN.∴△AEM≌△ACN(ASA)②选择△ABN≌△ADM,理由如下:∵△ADE≌△ABC,∴AB=AD,∠B=∠D.
∵∠BAN=∠DAM,∴△ABN≌△ADM(ASA).③选择△BMF≌△DNF,理由如下:
∵△ABN≌△ADM(由②可证),
∴AM=AN.∴BM=DN.∵∠B=∠D,∠BFM=∠DFN,
∴△BMF≌△DNF(AAS). 名师点评:证明有关线段或角相等,通常证三角形全等.
三角形全等的证明方法有 SAS,ASA,AAS,SSS.直角三角形
还有另外一种“HL”判定方法.1.(2012 年广东)已知三角形两边的长分别是 4 和 10,则此三角形第三边的长可能是()CA.5B.6C.11D.162.(2011 年广东茂名)如图 4-2-9,在△ABC 中,D,E 分别是 AB,AC 的中点,若 DE=5,则 BC=()A.6B.8C.10D.12图 4-2-9C 3.(2012 年广东梅州)如图 4-2-10,在折纸活动中,小明制
作了一张△ABC 纸片,点 D,E 分别在边 AB,AC 上,将△ABC
沿着 DE 折叠压平,A 与 A′重合,若∠A=75°,则∠1+∠2=()A图 4-2-10A.150°B.210°C.105°D.75°4.(2013 年广东珠海)如图4-2-11,已知,EC=AC,∠BCE图 4-2-11=∠DCA,∠A=∠E,求证:BC=DC.
证明:∵∠BCE=∠DCA,
∴∠BCE+∠ACE=∠DCA+∠ACE,
即∠BCA=∠DCE.
∵AC=EC,∠A=∠E,
∴△BCA≌△DCE(ASA).
∴BC=DC. 5.(2013 年广东佛山)课本指出:公认的真命题称为公理,
除了公理外,其他的真命题(如推论、定理等)的正确性都需要
通过推理的方法证实(如图 4-2-12).(1) 叙述三角形全等的判定方法中的推论 AAS;
(2) 证明推论 AAS.要求:叙述推论用文字表达;用图形中的符号表达已知、求证,并证明,证明对各步骤要注明依据.图 4-2-12解:(1)一个三角形的两个角和其中一个角的对边分别相等的两个三角形全等.(2)已知:在△ABC 和△DEF 中,
∠A=∠D,∠B=∠E,BC=EF,
求证:△ABC≌△DEF.证明:因为∠A +∠B +∠C =180° ,∠D +∠E +∠F =180°(三角形内角和定理),又∠A=∠D,∠B=∠E(已知),
所以∠C=∠F(等式的性质).在△ABC 和△DEF 中,∠B=∠E(已知),BC=EF(已知),∠C=∠F(已证),所以△ABC≌△DEF(ASA). 6.(2013年广东茂名)如图 4-2-13,已知:在矩形ABCD 中,
F 是 BC 上的一点,且 AF=BC , DE⊥AF ,垂足是 E,连接
DF.
求证:(1)△ABF≌△DEA;(2) DF 是∠EDC 的平分线.图 4-2-13证明:(1)∵四边形 ABCD 是矩形,
∴∠B=90°,AD=BC,AD∥BC.
∴∠DAE=∠AFB.
∵DE⊥AF, ∴∠DEA=∠B=90°.
∵AF=BC,∴AF=AD ∴. △ ABF≌△DEA.(2)证法一,由(1)知△ABF≌△DEA,∴DE=AB.
∵四边形 ABCD 是矩形,∴∠C=90°,DC=AB.∴DC=DE.∵∠DEA=90°,∴∠C=∠DEF=90°.
∵DF= DF ,∴ △ DCF≌ △ DEF.∴∠EDF=∠CDF.∴DF 是∠EDC 的平分线.
证法二,由(1)知△ABF≌△DEA,∴BF=EA.
∵AF=BC,∴EF=CF.∵∠DEA=90°,∴∠C=∠DEF=90°.
∴DF 是∠EDC 的平分线.
同课章节目录
