2014年中考总复习提能训练课件第四章 第3讲 第3课时梯形
文档属性
| 名称 | 2014年中考总复习提能训练课件第四章 第3讲 第3课时梯形 |

|
|
| 格式 | zip | ||
| 文件大小 | 340.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 12:40:03 | ||
图片预览





文档简介
课件19张PPT。第3课时梯形1.掌握梯形的概念和性质.
2.了解等腰梯形的有关性质和四边形是等腰梯形的条件.考点1梯形的有关概念及性质不平行 1.定义:一组对边平行,另一组对边____________的四边
形叫做梯形.
2.梯形的分类:
一般梯形
特殊梯形等腰梯形
直角梯形梯形考点2等腰梯形的性质与判定1.等腰梯形的性质.平行相等相等相等(1)两底__________,两腰__________.
(2)同一底上的两角__________.
(3)两条对角线____________.
(4)是轴对称图形.2.等腰梯形的判定.相等相等相等(1)两腰__________的梯形.
(2)同一底上的两角__________的梯形.
(3)对角线__________的梯形.【学有奇招】 1.梯形添加辅助线编成顺口溜为:有时平移腰,有时作出
高,有时平移对角线,有时延长两腰到相交,腰上有中点,赶
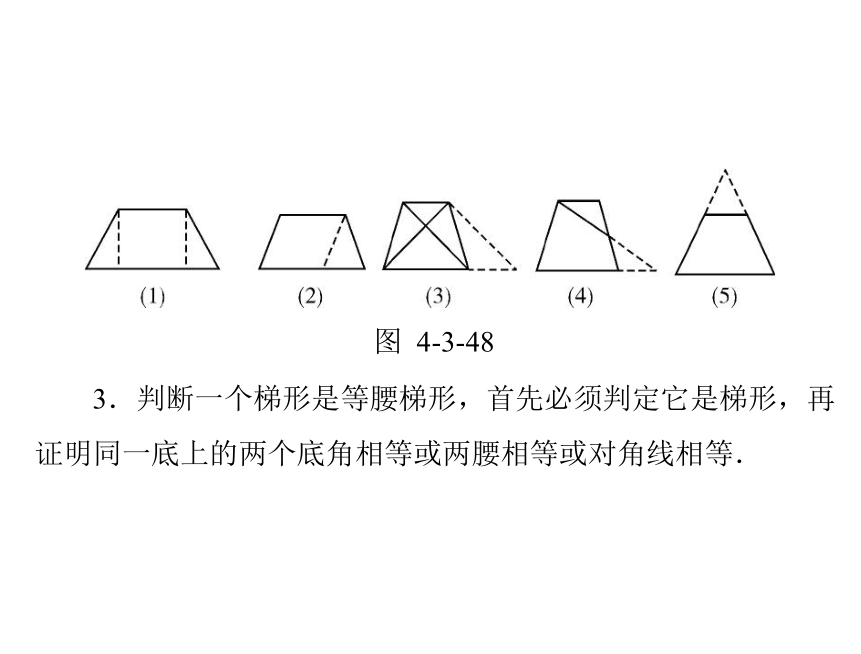
快作旋转,构造新图形,变得更明显.2.梯形中常见的辅助线作法: 解决梯形问题的基本思路和方法是添加适当的辅助线,将
梯形转化为四边形和三角形来研究和解决,添加辅助线的基本
思路是通过平移或旋转来实现.转化形式一般有以下几种(如图
4-3-48):图 4-3-48 3.判断一个梯形是等腰梯形,首先必须判定它是梯形,再
证明同一底上的两个底角相等或两腰相等或对角线相等.1.下列说法正确的是()BA.平行四边形是一种特殊的梯形
B.等腰梯形的两底角相等
C.等腰梯形可能是直角梯形
D.有两邻角相等的梯形是等腰梯形
2.在梯形ABCD中,AB∥DC,AD=DC=CB,若∠ABD=25°,则∠BAD 的大小是()CA.40°B.45°C.50°D.60°3.等腰梯形的中位线长是15 ,一条对角线平分一个60°的底角,则梯形的周长为______.50菱4.顺次连接等腰梯形四边中点所得的四边形是______形.B. 与梯形有关的计算
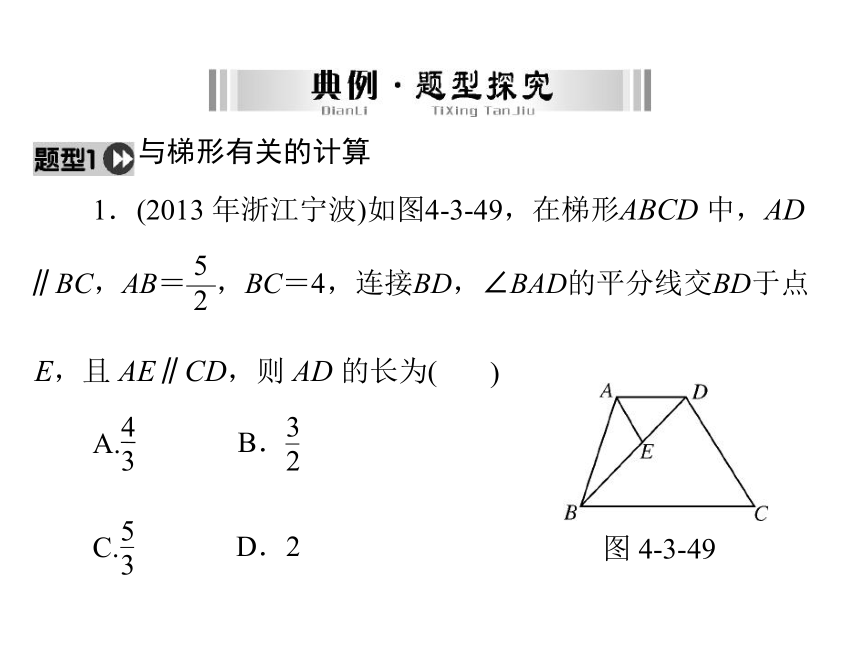
1.(2013 年浙江宁波)如图4-3-49,在梯形ABCD 中,AD
5
2E,且 AE∥CD,则 AD 的长为()A.4
33
2C.5
3D.2图 4-3-49∥BC,AB=—,BC=4,连接BD,∠BAD的平分线交BD于点 解析:延长 AE 交 BC 于 F,则容易得出四边形 ADCF 为平
行四边形,且∠BAF=∠AFB,则有 AD=FC=BC-BF=BC-答案:B2.已知:如图 4-3-50,在等腰梯形 ABCD 中,AD∥BC,)AAC⊥BD,AD=3,BC=7,则梯形的面积是(
图 4-3-50 名师点评:有关梯形的计算题型有三类:一是角的计算;
二是边的计算;三是面积的计算.等腰梯形的性质与判定 例题:(2013 年浙江杭州)如图 4-3-51,在等腰梯形 ABCD
中,AB∥DC,线段 AG,BG 分别交 CD 于点 E,F,DE=CF.求证:△GAB 是等腰三角形.图 4-3-51 思路分析:首先根据等腰梯形的性质得到AD=BC,∠D
=∠C,然后再根据SAS 证明△DEA≌△CFB,从而得到相关
角相等,进一步根据“等角对等边”的性质得出 AG=BG.解: ∵在等腰梯形ABCD 中,AD=BC,∠D=∠C,而 DE=CF,∴△DEA≌△CFB(SAS),则∠DAE=∠CBF.
又∵在等腰梯形ABCD 中,∠DAB=∠CBA,∴∠EAB=∠FBA,∴GA=GB.
则△GAB 为等腰三角形.【试题精选】
3.(2013 年广西钦州)如图 4-3-52,在梯形ABCD 中,AD
∥BC,AB∥DE,∠DEC=∠C.求证:梯形 ABCD 是等腰梯形.图 4-3-52证明:∵AB∥DE,∴∠B=∠DEC.
∵∠DEC=∠C,∴∠B=∠C.
又∵四边形 ABCD 是梯形,
∴梯形 ABCD 是等腰梯形. 1.(2012 年广东广州)如图 4-3-53,在等腰梯形 ABCD 中,
BC∥AD,AD=5,DC=4,DE∥AB 交 BC 于点 E,且 EC=3,则梯形 ABCD 的周长是()CA.26B.25C.21D.20图 4-3-53 2.(2013 年广东深圳)如图 4-3-54,在等腰梯形 ABCD 中,
已知 AD∥BC,AB=DC,AC 与 BD 交于点 O,延长 BC 到 E,
使得 CE=AD,连接 DE.(1)求证:BD=DE;(2)若 AC⊥BD,AD=3,S梯形 ABCD=16,求 AB 的长.图 4-3-54(1)证明:∵AD∥BC,AD=CE,
∴四边形 ADEC 为平行四边形.
∴AC=DE.
又∵ABCD 为等腰梯形,∴AC=DB.
∴BD=DE.
(2)解:分别过 A,D 作 AA′⊥BC,DD′⊥BC,如图 21,∴AA′=DD′,图 21在△BAD 和△DCE 中,
AD=CE,AB=CD,BD=DE,∴△BAD≌△DCE. 3.(2011 年广东茂名)如图 4-3-55,在等腰三角形 ABC 中,
点 D,E 分别是两腰 AC,BC 上的点,连接 AE,BD 相交于点
O,∠1=∠2.(1)求证:OD=OE;(2)求证:四边形 ABED 是等腰梯形;(3)若 AB=3DE, △DCE 的面积为 2, 求四边形 ABED 的面积.图 4-3-55(1)证明:∵△ABC 是等腰三角形,∴AC=BC.
∴∠BAD=∠ABE.
又∵AB=BA,∠2=∠1,
∴△ABD≌△BAE(ASA).∴BD=AE.
又∵∠1=∠2,∴OA=OB.
∴BD-OB=AE-OA,即 OD=OE.
(2)证明:由(1)知:OD=OE,∴∠OED=∠ODE.∴∠OED=1
2(180°-∠DOE).1
2 同理:∠1=—(180°-∠AOB).又∵∠DOE=∠AOB,∴∠1=∠OED.∴DE∥AB.
∵AD,BE 是等腰三角形两腰所在的线段,
∴AD 与 BE 不平行.∴四边形 ABED 是梯形.
又∵由(1)知,△ABD≌△BAE,∴AD=BE.
∴梯形 ABED 是等腰梯形.
(3)解:由(2)可知:DE∥AB,
∴∠CED=∠CBA,∠CDE=∠CAB ∴.DCE∽△ACB.
2.了解等腰梯形的有关性质和四边形是等腰梯形的条件.考点1梯形的有关概念及性质不平行 1.定义:一组对边平行,另一组对边____________的四边
形叫做梯形.
2.梯形的分类:
一般梯形
特殊梯形等腰梯形
直角梯形梯形考点2等腰梯形的性质与判定1.等腰梯形的性质.平行相等相等相等(1)两底__________,两腰__________.
(2)同一底上的两角__________.
(3)两条对角线____________.
(4)是轴对称图形.2.等腰梯形的判定.相等相等相等(1)两腰__________的梯形.
(2)同一底上的两角__________的梯形.
(3)对角线__________的梯形.【学有奇招】 1.梯形添加辅助线编成顺口溜为:有时平移腰,有时作出
高,有时平移对角线,有时延长两腰到相交,腰上有中点,赶
快作旋转,构造新图形,变得更明显.2.梯形中常见的辅助线作法: 解决梯形问题的基本思路和方法是添加适当的辅助线,将
梯形转化为四边形和三角形来研究和解决,添加辅助线的基本
思路是通过平移或旋转来实现.转化形式一般有以下几种(如图
4-3-48):图 4-3-48 3.判断一个梯形是等腰梯形,首先必须判定它是梯形,再
证明同一底上的两个底角相等或两腰相等或对角线相等.1.下列说法正确的是()BA.平行四边形是一种特殊的梯形
B.等腰梯形的两底角相等
C.等腰梯形可能是直角梯形
D.有两邻角相等的梯形是等腰梯形
2.在梯形ABCD中,AB∥DC,AD=DC=CB,若∠ABD=25°,则∠BAD 的大小是()CA.40°B.45°C.50°D.60°3.等腰梯形的中位线长是15 ,一条对角线平分一个60°的底角,则梯形的周长为______.50菱4.顺次连接等腰梯形四边中点所得的四边形是______形.B. 与梯形有关的计算
1.(2013 年浙江宁波)如图4-3-49,在梯形ABCD 中,AD
5
2E,且 AE∥CD,则 AD 的长为()A.4
33
2C.5
3D.2图 4-3-49∥BC,AB=—,BC=4,连接BD,∠BAD的平分线交BD于点 解析:延长 AE 交 BC 于 F,则容易得出四边形 ADCF 为平
行四边形,且∠BAF=∠AFB,则有 AD=FC=BC-BF=BC-答案:B2.已知:如图 4-3-50,在等腰梯形 ABCD 中,AD∥BC,)AAC⊥BD,AD=3,BC=7,则梯形的面积是(
图 4-3-50 名师点评:有关梯形的计算题型有三类:一是角的计算;
二是边的计算;三是面积的计算.等腰梯形的性质与判定 例题:(2013 年浙江杭州)如图 4-3-51,在等腰梯形 ABCD
中,AB∥DC,线段 AG,BG 分别交 CD 于点 E,F,DE=CF.求证:△GAB 是等腰三角形.图 4-3-51 思路分析:首先根据等腰梯形的性质得到AD=BC,∠D
=∠C,然后再根据SAS 证明△DEA≌△CFB,从而得到相关
角相等,进一步根据“等角对等边”的性质得出 AG=BG.解: ∵在等腰梯形ABCD 中,AD=BC,∠D=∠C,而 DE=CF,∴△DEA≌△CFB(SAS),则∠DAE=∠CBF.
又∵在等腰梯形ABCD 中,∠DAB=∠CBA,∴∠EAB=∠FBA,∴GA=GB.
则△GAB 为等腰三角形.【试题精选】
3.(2013 年广西钦州)如图 4-3-52,在梯形ABCD 中,AD
∥BC,AB∥DE,∠DEC=∠C.求证:梯形 ABCD 是等腰梯形.图 4-3-52证明:∵AB∥DE,∴∠B=∠DEC.
∵∠DEC=∠C,∴∠B=∠C.
又∵四边形 ABCD 是梯形,
∴梯形 ABCD 是等腰梯形. 1.(2012 年广东广州)如图 4-3-53,在等腰梯形 ABCD 中,
BC∥AD,AD=5,DC=4,DE∥AB 交 BC 于点 E,且 EC=3,则梯形 ABCD 的周长是()CA.26B.25C.21D.20图 4-3-53 2.(2013 年广东深圳)如图 4-3-54,在等腰梯形 ABCD 中,
已知 AD∥BC,AB=DC,AC 与 BD 交于点 O,延长 BC 到 E,
使得 CE=AD,连接 DE.(1)求证:BD=DE;(2)若 AC⊥BD,AD=3,S梯形 ABCD=16,求 AB 的长.图 4-3-54(1)证明:∵AD∥BC,AD=CE,
∴四边形 ADEC 为平行四边形.
∴AC=DE.
又∵ABCD 为等腰梯形,∴AC=DB.
∴BD=DE.
(2)解:分别过 A,D 作 AA′⊥BC,DD′⊥BC,如图 21,∴AA′=DD′,图 21在△BAD 和△DCE 中,
AD=CE,AB=CD,BD=DE,∴△BAD≌△DCE. 3.(2011 年广东茂名)如图 4-3-55,在等腰三角形 ABC 中,
点 D,E 分别是两腰 AC,BC 上的点,连接 AE,BD 相交于点
O,∠1=∠2.(1)求证:OD=OE;(2)求证:四边形 ABED 是等腰梯形;(3)若 AB=3DE, △DCE 的面积为 2, 求四边形 ABED 的面积.图 4-3-55(1)证明:∵△ABC 是等腰三角形,∴AC=BC.
∴∠BAD=∠ABE.
又∵AB=BA,∠2=∠1,
∴△ABD≌△BAE(ASA).∴BD=AE.
又∵∠1=∠2,∴OA=OB.
∴BD-OB=AE-OA,即 OD=OE.
(2)证明:由(1)知:OD=OE,∴∠OED=∠ODE.∴∠OED=1
2(180°-∠DOE).1
2 同理:∠1=—(180°-∠AOB).又∵∠DOE=∠AOB,∴∠1=∠OED.∴DE∥AB.
∵AD,BE 是等腰三角形两腰所在的线段,
∴AD 与 BE 不平行.∴四边形 ABED 是梯形.
又∵由(1)知,△ABD≌△BAE,∴AD=BE.
∴梯形 ABED 是等腰梯形.
(3)解:由(2)可知:DE∥AB,
∴∠CED=∠CBA,∠CDE=∠CAB ∴.DCE∽△ACB.
同课章节目录
