2014年中考总复习提能训练课件第五章 第1讲圆的基本性质
文档属性
| 名称 | 2014年中考总复习提能训练课件第五章 第1讲圆的基本性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 541.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 12:38:03 | ||
图片预览







文档简介
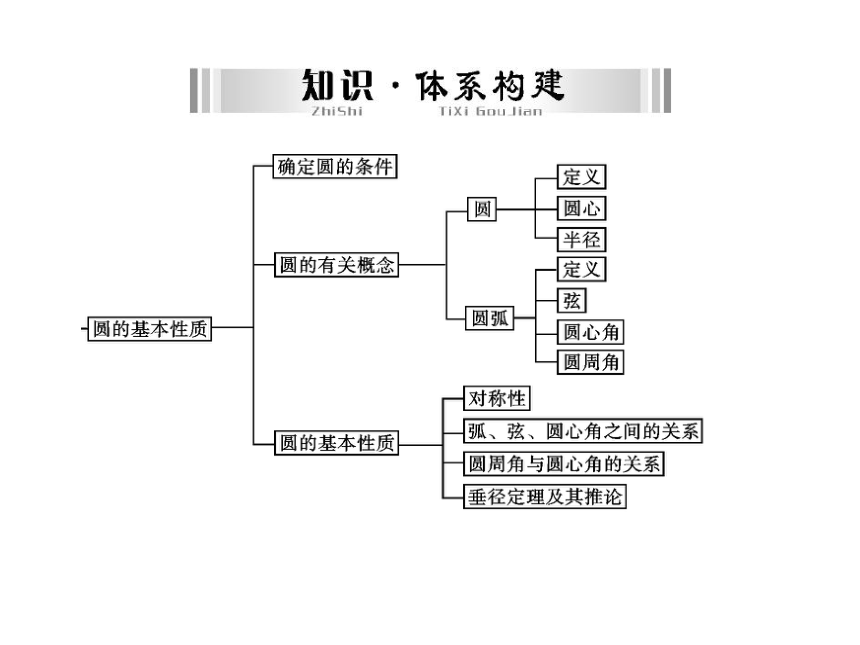
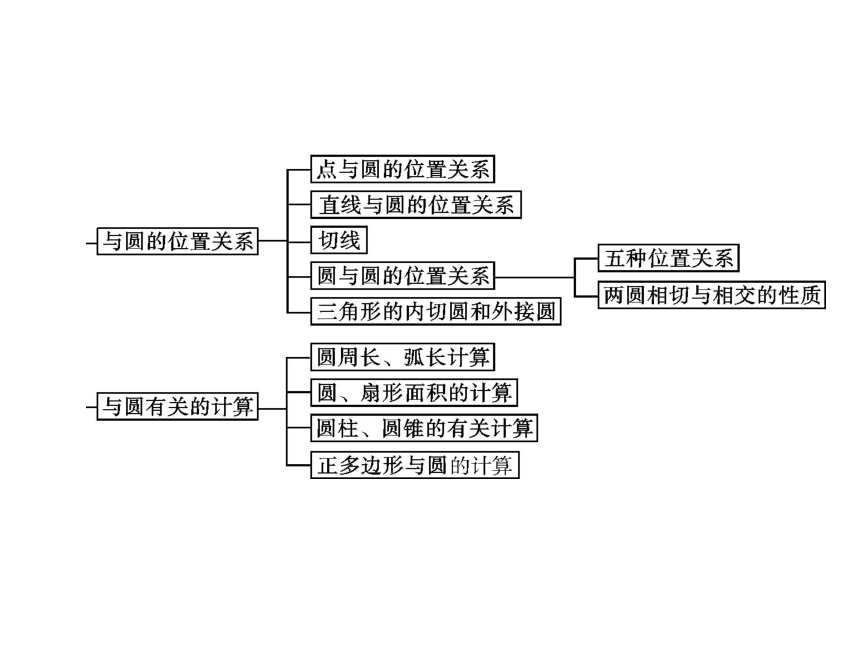
课件25张PPT。第五章 圆第1讲圆的基本性质1.理解圆及其有关概念、了解弧、弦、圆心角的关系.
2.了解圆周角与圆心角的关系、直径所对圆周角的特征.考点1圆的有关概念及性质1.圆.定点定长轴中心三点 (1) 平面上到__________ 的距离等于________ 的所有点组
成的图形叫做圆.
(2)圆是________对称图形,也是__________对称图形.
(3)不共线的________可确定一个圆.2.垂径定理及其推论.
(1)定理:垂直于弦的直径______这条弦,并且______弦所对的弧.平分平分垂直弧圆心(2)推论 1:弦弧 ①平分弦(不是直径)的直径______于弦,并且平分弦所对
的________;
②弦的垂直平分线经过______,并且平分弦所对的两条弧;
③平分弦所对的一条弧的直径垂直平分_____,并且平分弦
所对的另一条弧.
(3)推论 2:圆的两条平行弦所夹的_____相等.(4)垂径定理及其推论可概括为:
过圆心
垂直于弦平分弦知二推三 平分弦所对的优弧
平分弦所对的劣弧
3.圆心角、弧、弦的关系.
(1)定理:在同圆或等圆中,相等的__________所对的弧相等,所对的弦相等.圆心角两条弧 (2)推论:在同圆或等圆中,如果两个圆心角、_______、两条
弦中有一组量相等,那么它们所对应的其余各组量都分别相等.考点2与圆有关的角及其性质 1.圆心角:顶点在__________,角的两边和圆相交的角.
圆周角:顶点在__________,角的两边和圆相交的角.
2.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周
角相等,等于它所对的圆心角的________.
推论:直径所对的圆周角是________,90°的圆周角所对的弦是直径.圆心圆上一半直角【学有奇招】1.在应用垂径定理及其推论进行计算时,往往要构造直角三角形,根据垂径定理及勾股定理进行求解. 2.圆中解题不要嫌,常把半径直径连;有弦可作弦心距,
肯定垂直平分弦;弧有中点圆心连,垂径定理要记全;直径是
圆最大弦,直圆周角立上边,直径如果垂直弦,垂径定理在手
边;还有与圆相关角,勿忘相互有关联,同弧圆周角相等,证
题用它最常见.1.如图 5-1-1,AB 是⊙O 的直径,CD 为⊙O 的弦,CD⊥)DAB 于 E,则下列结论不成立的是(
A.∠A=∠D
B.CE=DE
C. ∠ACB=90°
D.BD=CE图 5-1-12.如图 5-1-2,⊙O 的弦AB垂直平分半径OC,若 AB= ,则⊙O 的半径为()A图 5-1-2图 5-1-33.如图 5-1-3,∠AOB=100°,点 C 在⊙O 上,且点 C 不与点 A,B 重合,则∠ACB 的度数为()DA.50°B.80°或 50°C.130°D.50°或 130° 4.如图 5-1-4,C 是劣弧 AB 的中点,过点 C 分别作 CD⊥
OA,CE⊥OB,点 D,E 分别是垂足,试判断 CD,CE 的大小
关系,并证明你的结论.
解:CD=CE.理由:连接 CO.
∵C 是弧 AB 的中点,
∵CD⊥AO,CE⊥BO,∴∠CDO=∠CEO=90°.
又∵CO=CO,∴△COD≌△COE.∴CD=CE.图5-1-4 垂径定理的简单应用
例题:(2013 年甘肃兰州)图 5-1-5 是一圆柱形输水管的横截
面,阴影部分为有水部分,如果水面 AB 宽为 8 cm,水的最大)深度为 2 cm,则该输水管的半径为(
A.3 cm
B.4 cm
C.5 cm
D.6 cm图 5-1-5∵OD⊥AB,∴AD=—AB=—×8=4(cm).解析:如图5-1-5,过点O 作OD⊥AB 于点D,连接OA.1 1
2 2设 OA=r,则 OD=r-2.在Rt△AOD 中,OA2=OD2+AD2,
即r2=(r-2)2+42,解得 r=5 cm.
答案:C【试题精选】
1.( 2013 年黑龙江牡丹江)在半径为 13 的⊙O 中,弦 AB∥CD,弦 AB 和 CD 的距离为 7.若 AB=24,则 CD 的长为()(1)(2)图22答案:D 2.(2013 年湖南邵阳)如图 5-1-6,某窗户是由矩形和弓形
组成,已知弓形的跨度 AB=3 m,弓形的高 EF=1 m,现计划图 5-1-6安装玻璃,请帮工程师求出 所在圆 O 的半径 r.
名师点评:垂径定理及其推论是证明两线段相等,两条弧
相等及两直线垂直的重要依据之一,在有关弦长的计算中常常
需要添加辅助线(半径或弦心距).利用垂径定理及其推论(“平
分弦”为条件时,弦不能是直径),将其转化为直角三角形,应
用勾股定理计算. 圆心角与圆周角之间的关系
3. (2013 年福建厦门)如图 5-1-7,在⊙O 中, = ,∠A=30°,则∠B=()BA.150°B.75°C.60°D.15°图 5-1-7 4. (2013 年湖南株洲)如图5-1-8,AB 是⊙O的直径,∠BAC
=42°,点 D 是弦 AC 的中点,则∠DOC 的度数是_____度.图 5-1-8名师点评:当涉及弦所对的弧时应分两种情况:弦所对的弧可能是优弧,也可能是劣弧.481.(2013 年广东佛山)半径为3的圆中,一条弦长为 4,则圆心到这条弦的距离是()C2.(2013年广东湛江)如图5-1-9,AB 是⊙O 的直径,∠AOC=110°,则∠D=(
A.25°
C.55° )
B.35°
D.70°
图 5-1-9B 3.(2013 年广东珠海)如图 5-1-10,?ABCD 的顶点 A,B,
D 在⊙O 上,顶点C在⊙O的直径 BE 上,∠ADC=54°,连接BE,则∠AEB 的度数为()AA.36°B.46°C.27°D.63°图 5-1-10图 5-1-114.(2013 年广东佛山)图 5-1-11 中的圆心角∠AOB=30°,弦 CA∥OB,延长 CO 与圆交于点 D,则∠BOD=_____.30° 5.(2013 年广东广州)如图 5-1-12,在平面直角坐标系中,
点 O 为坐标原点,点 P 在第一象限,⊙P 与 x 轴交于 O,A 两
点,点 A 的坐标为(6,0),⊙P 的半径为 ,则点 P 的坐标为____________.(3,2)图 5-1-12解析:作 PB⊥OA 于点 B,连接 PO.
∵点 A 的坐标为(6,0),∴OB=3.
在 Rt△POB 中,PO= ,OB=3,
∴由勾股定理求得 PB=2,则点 P 的坐标是(3,2),
故答案填(3,2). 6.(2012 年广东河源)如图 5-1-13,AC是⊙O的直径,弦
BD 交 AC 于点 E.
(1)求证:△ADE∽△BCE;图 5-1-13(2)如果 AD2=AE·AC,求证:CD=CB.
证明:(1)∵ = ,
∴∠ADE=∠BCE.
又∵∠AED=∠BEC,
∴△ADE∽△BCE.
2.了解圆周角与圆心角的关系、直径所对圆周角的特征.考点1圆的有关概念及性质1.圆.定点定长轴中心三点 (1) 平面上到__________ 的距离等于________ 的所有点组
成的图形叫做圆.
(2)圆是________对称图形,也是__________对称图形.
(3)不共线的________可确定一个圆.2.垂径定理及其推论.
(1)定理:垂直于弦的直径______这条弦,并且______弦所对的弧.平分平分垂直弧圆心(2)推论 1:弦弧 ①平分弦(不是直径)的直径______于弦,并且平分弦所对
的________;
②弦的垂直平分线经过______,并且平分弦所对的两条弧;
③平分弦所对的一条弧的直径垂直平分_____,并且平分弦
所对的另一条弧.
(3)推论 2:圆的两条平行弦所夹的_____相等.(4)垂径定理及其推论可概括为:
过圆心
垂直于弦平分弦知二推三 平分弦所对的优弧
平分弦所对的劣弧
3.圆心角、弧、弦的关系.
(1)定理:在同圆或等圆中,相等的__________所对的弧相等,所对的弦相等.圆心角两条弧 (2)推论:在同圆或等圆中,如果两个圆心角、_______、两条
弦中有一组量相等,那么它们所对应的其余各组量都分别相等.考点2与圆有关的角及其性质 1.圆心角:顶点在__________,角的两边和圆相交的角.
圆周角:顶点在__________,角的两边和圆相交的角.
2.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周
角相等,等于它所对的圆心角的________.
推论:直径所对的圆周角是________,90°的圆周角所对的弦是直径.圆心圆上一半直角【学有奇招】1.在应用垂径定理及其推论进行计算时,往往要构造直角三角形,根据垂径定理及勾股定理进行求解. 2.圆中解题不要嫌,常把半径直径连;有弦可作弦心距,
肯定垂直平分弦;弧有中点圆心连,垂径定理要记全;直径是
圆最大弦,直圆周角立上边,直径如果垂直弦,垂径定理在手
边;还有与圆相关角,勿忘相互有关联,同弧圆周角相等,证
题用它最常见.1.如图 5-1-1,AB 是⊙O 的直径,CD 为⊙O 的弦,CD⊥)DAB 于 E,则下列结论不成立的是(
A.∠A=∠D
B.CE=DE
C. ∠ACB=90°
D.BD=CE图 5-1-12.如图 5-1-2,⊙O 的弦AB垂直平分半径OC,若 AB= ,则⊙O 的半径为()A图 5-1-2图 5-1-33.如图 5-1-3,∠AOB=100°,点 C 在⊙O 上,且点 C 不与点 A,B 重合,则∠ACB 的度数为()DA.50°B.80°或 50°C.130°D.50°或 130° 4.如图 5-1-4,C 是劣弧 AB 的中点,过点 C 分别作 CD⊥
OA,CE⊥OB,点 D,E 分别是垂足,试判断 CD,CE 的大小
关系,并证明你的结论.
解:CD=CE.理由:连接 CO.
∵C 是弧 AB 的中点,
∵CD⊥AO,CE⊥BO,∴∠CDO=∠CEO=90°.
又∵CO=CO,∴△COD≌△COE.∴CD=CE.图5-1-4 垂径定理的简单应用
例题:(2013 年甘肃兰州)图 5-1-5 是一圆柱形输水管的横截
面,阴影部分为有水部分,如果水面 AB 宽为 8 cm,水的最大)深度为 2 cm,则该输水管的半径为(
A.3 cm
B.4 cm
C.5 cm
D.6 cm图 5-1-5∵OD⊥AB,∴AD=—AB=—×8=4(cm).解析:如图5-1-5,过点O 作OD⊥AB 于点D,连接OA.1 1
2 2设 OA=r,则 OD=r-2.在Rt△AOD 中,OA2=OD2+AD2,
即r2=(r-2)2+42,解得 r=5 cm.
答案:C【试题精选】
1.( 2013 年黑龙江牡丹江)在半径为 13 的⊙O 中,弦 AB∥CD,弦 AB 和 CD 的距离为 7.若 AB=24,则 CD 的长为()(1)(2)图22答案:D 2.(2013 年湖南邵阳)如图 5-1-6,某窗户是由矩形和弓形
组成,已知弓形的跨度 AB=3 m,弓形的高 EF=1 m,现计划图 5-1-6安装玻璃,请帮工程师求出 所在圆 O 的半径 r.
名师点评:垂径定理及其推论是证明两线段相等,两条弧
相等及两直线垂直的重要依据之一,在有关弦长的计算中常常
需要添加辅助线(半径或弦心距).利用垂径定理及其推论(“平
分弦”为条件时,弦不能是直径),将其转化为直角三角形,应
用勾股定理计算. 圆心角与圆周角之间的关系
3. (2013 年福建厦门)如图 5-1-7,在⊙O 中, = ,∠A=30°,则∠B=()BA.150°B.75°C.60°D.15°图 5-1-7 4. (2013 年湖南株洲)如图5-1-8,AB 是⊙O的直径,∠BAC
=42°,点 D 是弦 AC 的中点,则∠DOC 的度数是_____度.图 5-1-8名师点评:当涉及弦所对的弧时应分两种情况:弦所对的弧可能是优弧,也可能是劣弧.481.(2013 年广东佛山)半径为3的圆中,一条弦长为 4,则圆心到这条弦的距离是()C2.(2013年广东湛江)如图5-1-9,AB 是⊙O 的直径,∠AOC=110°,则∠D=(
A.25°
C.55° )
B.35°
D.70°
图 5-1-9B 3.(2013 年广东珠海)如图 5-1-10,?ABCD 的顶点 A,B,
D 在⊙O 上,顶点C在⊙O的直径 BE 上,∠ADC=54°,连接BE,则∠AEB 的度数为()AA.36°B.46°C.27°D.63°图 5-1-10图 5-1-114.(2013 年广东佛山)图 5-1-11 中的圆心角∠AOB=30°,弦 CA∥OB,延长 CO 与圆交于点 D,则∠BOD=_____.30° 5.(2013 年广东广州)如图 5-1-12,在平面直角坐标系中,
点 O 为坐标原点,点 P 在第一象限,⊙P 与 x 轴交于 O,A 两
点,点 A 的坐标为(6,0),⊙P 的半径为 ,则点 P 的坐标为____________.(3,2)图 5-1-12解析:作 PB⊥OA 于点 B,连接 PO.
∵点 A 的坐标为(6,0),∴OB=3.
在 Rt△POB 中,PO= ,OB=3,
∴由勾股定理求得 PB=2,则点 P 的坐标是(3,2),
故答案填(3,2). 6.(2012 年广东河源)如图 5-1-13,AC是⊙O的直径,弦
BD 交 AC 于点 E.
(1)求证:△ADE∽△BCE;图 5-1-13(2)如果 AD2=AE·AC,求证:CD=CB.
证明:(1)∵ = ,
∴∠ADE=∠BCE.
又∵∠AED=∠BEC,
∴△ADE∽△BCE.
同课章节目录
