2014年中考总复习提能训练课件高频错题集锦(共39张PPT)
文档属性
| 名称 | 2014年中考总复习提能训练课件高频错题集锦(共39张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 394.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 12:14:50 | ||
图片预览










文档简介
课件39张PPT。高频错题集锦易错点1:对绝对值的几何意义理解不透例题:点 A 在数轴上表示的数是-1,点 B 表示的数的绝对值是 3.则线段 AB 的距离是__________. 分析:B 点表示的数的绝对值是 3,说明B 点到原点的距
离是3,这样的 B 点有2 个,位于原点的左右两边,分别是-3
和 3.所以线段AB 的距离也有2 种情况,如图G-1图 G-1正解:4 或 2 失误与防范:易错误地认为点 B 表示的数只有 3,而忽略
-3,防范这种错误的方法是牢记绝对值的几何意义.易错点2:混淆幂的运算法则例题:下列运算中,正确的是() 分析:A 中a5+a5 合并同类项后等于2a5;B中(a2)3 是幂
的乘方运算,指数相乘等于a6 ;C 是同底数幂相除指数相减等
于a4;D 中 a2a3 是同底数幂相乘指数相加等于a5.
正解:D
失误与防范:易混淆幂的运算法则,幂的运算法则较多,
一定要分清楚记牢.A.a5+a5=2a10 B.(a2)3=a5
C.a6÷a2=a3 D.a2a3=a5易错点3:完全平方公式中的交叉项可正可负例题:如果 a2-ka+1 是一个完全平方式,那么 k 的值是________. 分析:当k=2 时,a2-ka+1=a2-2a+1 是一个完全平方
式;当k=-2 时,a2-ka+1=a2+2a+1 也是一个完全平方式.正解:k=2 或-2 失误与防范:错误的原因是没有注意到完全平方公式中的
交叉项可正可负,防范这种错误的方法是牢记公式.易错点 4:二次根式化简时,没注意字母中隐含的负号数,所以化简的结果一定是正数,所以 D 错误.
正解:B失误与防范:错误的原因是没注意字母 a 中隐含的负号,把 a 当成一个正数来计算. 防范这种错误的方法注意字母中隐含的负号,同时注
意中的两个非负性:①被开方数非负;②表示的是一个算
术平方根,是一个非负数.易错点 5:方程两边同时除以一个等于 0 的代数式例题:方程 x(x-1)=x 的根是()A.x=1
C.x1=0,x2=2B.x=2
D.x1=0,x2=1 分析:当x=0 时,方程两边相等,即x=0 是方程的一个
根;当 x≠0 时,原方程同时除以 x,得x-1=1,即x=2.
正解:C
失误与防范:错误的原因是方程两边同时除以 x,忽略 x
可能为 0,这时就造成了失根.防范这种错误的方法是解方程
时,如果方程的两边同时除以一个代数式,一定要注意它是否
会等于 0. 易错点6:确定不等式组的解集时,要注意其中的字母是
否可以等于边界值例题:已知不等式组3+2x≥1,
x-a<0无解,则 a 的取值范围是________.
分析:由不等式3+2x≥1,得x≥-1,由不等式x-a<0,
得 x<a,依据不等式组解集的确定法则确定 a 的值.
正解:a≤-1失误与防范:错误的原因是在确定x≥-1,
x值范围定为 a<-1.这是此类题最容易犯的一个错误.防范这种
错误的方法是确定不等式组的解集时要注意其中的字母是否可
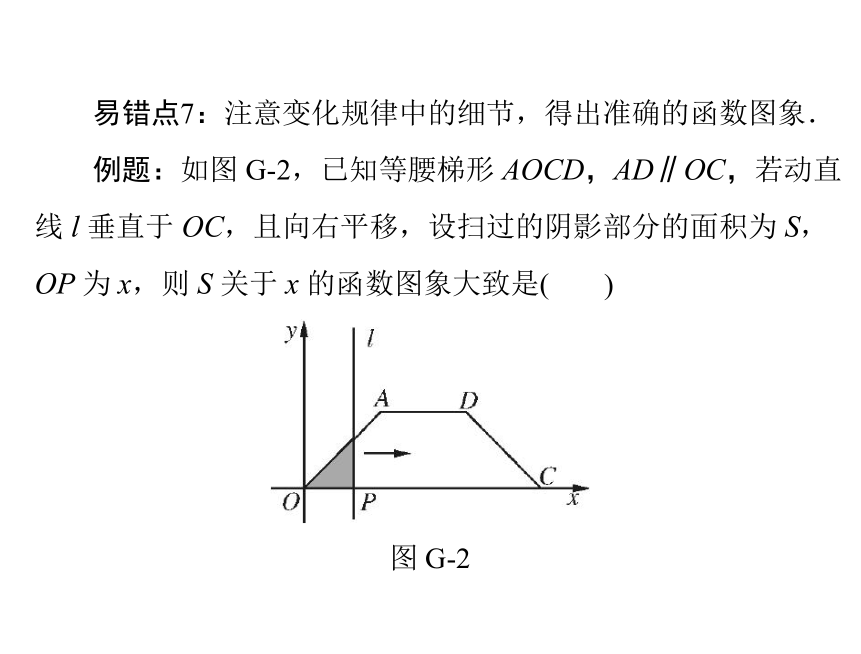
以取边界值. 易错点7:注意变化规律中的细节,得出准确的函数图象.
例题:如图 G-2,已知等腰梯形 AOCD,AD∥OC,若动直
线 l 垂直于 OC,且向右平移,设扫过的阴影部分的面积为 S,)OP 为 x,则 S 关于 x 的函数图象大致是(
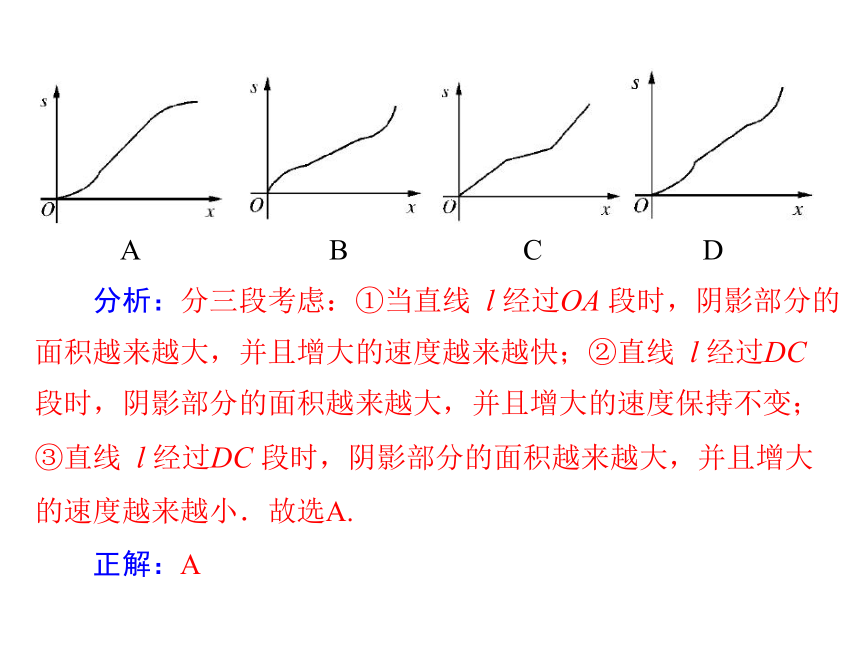
图 G-2ABCD 分析:分三段考虑:①当直线 l 经过OA 段时,阴影部分的
面积越来越大,并且增大的速度越来越快;②直线 l 经过DC
段时,阴影部分的面积越来越大,并且增大的速度保持不变;
③直线 l 经过DC 段时,阴影部分的面积越来越大,并且增大
的速度越来越小.故选A.
正解:A 失误与防范:错误的原因是忽略对阴影部分的面积增加的
速度进行细节分析,从而选择错误的选项 C.防范这种错误的方
法是仔细观察图形的变化细节,才能更准确地得出函数图象的
变化特点.例题:反比例函数 y=—,当 x≤3 时,y 的取值范围是(C.y≥—或 y<0易错点 8:注意反比例函数的图象有两支2
x)A.y≤2
3B.y≥2
32
3D.03 正解:C 易错点9:不清楚二次函数 y=ax2+bx+c(a≠0)的图象特
点与系数 a,b,c 的关系
例题:已知二次函数 y=ax2+bx+c 的图象如图 G-3,对称
轴是直线 x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac)图 G-3<0;④4a+2b+c>0.其中正确的是(
A.①③
B.只有②
C.②④
D.③④
正解:C 失误与防范:错误的原因:二次函数y=ax2+bx+c(a≠0)
的图象特点与系数a,b,c 的关系不是很熟悉,特别容易因为
一个符号的错误造成整个题目的错误.防范这种错误的方法:
记住:①a 的符号决定抛物线的开口方向;②a,b 的符号共同
决定对称轴的位置.a,b 同号对称轴在 y 轴的左侧,a,b 异号
对称轴在y 轴的右侧;③c的符号决定抛物线与 y 轴的交点(0,
c)的位置,c>0 交点在y 轴的正半轴,c<0 交点在 y 轴的负半轴.易错点10:对平行线判定不准确)例题:如图 G-4,在下列条件中,能判断 AD∥BC 的是(
A.∠DAC=∠BCA
B.∠DCB+∠ABC=180°
C.∠ABD=∠BDCD.∠BAC=∠ACD图 G-4 分析:∠DAC 和∠BCA 是直线 AD 和直线 BC 被 AC 所截
形成的内错角,又∵∠DAC=∠BCA,∴AD∥BC.
正解:A 失误与防范:关键是判断选项中两个角是不是直线 AD,
BC 被第三条直线所截形成的两角(同位角、内错角、同旁内角),
再观察是不是符合 AD∥BC 的判定方法. 易错点 11:涉及等腰三角形的高时出现的漏解
例题:等腰三角形一腰上的高与另一腰所成的夹角为 45°,
求这个等腰三角形的顶角的度数.
分析:容易出现漏解.如图G-5(1),因为 CD 是腰AB 边上
的高,且∠ACD=45°,则这个等腰三角形的顶角为45°.(1)(2)图G-5正解:依题意可画出图 G-5(1)(2)两种情形,显然,易求得图(1)中的顶角为 45°和(2)中的顶角为135°. 失误与防范:三角形的高是由三角形的形状所决定的.对
于等腰三角形,当顶角是锐角时,腰上的高在三角形内;当顶
角是钝角时,腰上的高在三角形外.所以应分两种情况进行讨
论. 易错点 12:对平行四边形的判定方法把握不准导致漏解
例题:四边形 ABCD 中,对角线 AC,BD 相交于点 O,给
出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB
=OD.
从中任选两个条件,能使四边形 ABCD 为平行四边形的选法有()A.3 种
C.5 种B.4 种
D.6 种 分析:从一组对边平行且相等(①②),对角线互相平分(③
④),以及条件组合(①③、①④),通过判定三角形全等进一步
判定四边形为平行四边形,仅仅满足条件②③或者是②④不能
证明三角形全等,故选法有 4 种.正解:B易错点13:概念不清,审题不到位导致推理不严密 例题:如图G-6,在菱形ABCD 中,对角线 AC 和 BD 相交
于点 O,OE⊥AB 于点 E,OF⊥BC 于点 F,OG⊥CD 于点 G,
OH⊥AD于点 H,依次连接 EF,FG,GH,HE,试说明四边形
EFGH 为矩形.图 G-6正解:因为OG⊥CD,AB∥CD,所以 OG⊥AB.又OE⊥AB,由垂直公理,得直线OE 和OG 为同一条直线,则E,O,G 三点共线.从而EG 为四边形EFGH 的对角线.同理,可得FH 也是四边形EFGH 的对角线.
因为BD为菱形ABCD 的对角线,
所以∠ABD=∠CBD.又因为OE⊥AB,OF⊥BC,由角平分线性质定理,可得 OE=OF.同理,可得OF=OG,OG=OH,OH=OE.
即OE=OF=OG=OH.所以四边形 EFGH 为平行四边形.因为 OE+OG=OF+OH,即 EG=FH.
所以四边形 EFGH 为矩形. 失误与防范:本题估计很多同学会先说明四边形EFGH 的
“对角线EG 和FH 互相平分”,可得四边形EFGH 为平行四
边形,再说明“对角线EG=FH”,从而得到结论:四边形EFGH
为矩形.表面上看来似乎推理严谨,无懈可击,其实不然.解
本题的关键是说明E,O,G 和 F,O,H 分别是同一条直线上
的三点(也就是三点共线). 易错点14:概念模糊
例题:已知在四边形 ABCD 中,AB =DC ,AC =BD ,
AD≠BC,试说明四边形 ABCD 是等腰梯形.
正解:如图G-7,过点D 作 DE∥AC,交BC 的延长线于点 E,图G-7在△ABC 和△DCB 中,
AB=DC,AC=DB,BC=CB,
所以△ABC≌△DCB.所以∠ACB=∠DBC.
因为DE ∥ AC,所以∠DEC=∠ACB=∠DBC.
所以DE=DB=AC.因为DE ∥ AC,DE=AC,所以四边形ACED 为平行四边形.
所以AD ∥ CE,即AD ∥ BC.因为AD≠BC,所以延长BA,CD 必相交.
所以AB 与DC 不平行.四边形ABCD 的一组对边AD,BC 平行,而另一组对边AB与 DC 不平行,所以四边形ABCD 为梯形.又因为AB=DC,所以四边形ABCD 为等腰梯形. 失误与防范:由于概念模糊,根据一组对边平行,就认定
这个四边形是梯形,这是不正确的.因为满足这个条件的四边
形既可能是梯形,也可能是平行四边形.因此还须说明这个四
边形的另一组对边不平行. 易错点 15:一条弦所对圆周角的值有两个
例题:在半径为 R 的圆内,求长为 R 的弦所对的圆周角.
正解:如图G-8,当圆周角的顶点在优弧上时,⊙O 的半
径为R,AB=R,∠ACB 为弦AB 所对的圆周角,连接OA,OB,
则 OA=OB=AB=R,∴ △OAB 为等边三角形.
1
2图G-8图G-9∴∠AOB=60°,∴∠ACB=—∠AOB=30°.如图G-9,当长为 R 的弦AB 所对的圆周角的顶点在劣弧AB 上时,连接OA,OB,同理可得△OAB 为等边三角形,
∴∠AOB=60°.∴优弧AMB 所对的圆心角为360°-60°=300°.
∴优弧AMB 所对的圆周角∠ACB=150°.
∴长为R 的弦所对的圆周角为30°或150°. 失误与防范:产生错解的原因是只考虑了长为 R 的弦所对
的圆周角的顶点在优弧上,而忽略了圆周角的顶点在劣弧上的
情况.易错点16:误认为若圆与线段只有一个公共点,则圆与线段相切 例题:如图G-10,在Rt△ABC中,∠C=90°,AC=3,BC
=4,若以 C 为圆心,R 为半径的圆与斜边只有一个公共点,则
R 的取值范围是______________________________.图 G-10 正解:①如图G-11,以C为圆心,R为半径的圆与斜边AB
相切.图G-11图 G-12AC·BC 3×4 12∴R=CD=AB 5 5= = =2.4. ②如图 G-12 所示,以点 C 为圆心,R 为半径的圆与斜边
AB 相交于一点,那么 R 应满足 AC<R≤ BC,即 3<R≤ 4.所以当 R=2.4 或 3<R≤4 时,圆与线段只有一个公共点. 失误与防范:产生错解的原因是误认为圆与斜边只有一个
公共点与圆与斜边相切等价,本题圆与斜边只有一个公共点分
两种情况:斜边与圆相切和线段与圆相交,都只有一个公共点.易错点 17:三视图中虚实线意义不明
例题:如图 G-13,正方体表面上画有一圈黑色线条,则它的左视图是()图 G-13ABCD正解:B 失误与防范:正方体中左边的虚线表示在观察时看不到的
轮廓线,而在它的左视图中是可见的实线,故在画左视图中应
画成实线.易错点18:应用性质解题时出现的错误
例题:如图G-14,在△ABC中,DE∥BC, S△ADE:S梯形BCED=1∶3,求 AD∶DB 的值.图 G-14 失误与防范:(1)相似三角形的面积比等于相似比的平方;
(2)由面积求相似比时,是开方求算术平方根,而不是平方.-x+2 x2-4易错点19:不清楚分式的基本性质致误例题:化简分式2 x-6. 失误与防范:分式的化简容易与解分式方程混淆,方式方
程根据等式的基本性质,需要去分母进行化简,分式的化简只
能通分和约分,不能随便去分母,解题时注意每一步过程都有
据可依,就不会出错.易错点20:不清楚分式有意义和除式有意义的条件致误三个数中选一个合适的,代入求值. 失误与防范:解分式化简后代入求值问题时,必须把即将
代入的值先代入原式,检查原式是否有意义.本题中要求分式
离是3,这样的 B 点有2 个,位于原点的左右两边,分别是-3
和 3.所以线段AB 的距离也有2 种情况,如图G-1图 G-1正解:4 或 2 失误与防范:易错误地认为点 B 表示的数只有 3,而忽略
-3,防范这种错误的方法是牢记绝对值的几何意义.易错点2:混淆幂的运算法则例题:下列运算中,正确的是() 分析:A 中a5+a5 合并同类项后等于2a5;B中(a2)3 是幂
的乘方运算,指数相乘等于a6 ;C 是同底数幂相除指数相减等
于a4;D 中 a2a3 是同底数幂相乘指数相加等于a5.
正解:D
失误与防范:易混淆幂的运算法则,幂的运算法则较多,
一定要分清楚记牢.A.a5+a5=2a10 B.(a2)3=a5
C.a6÷a2=a3 D.a2a3=a5易错点3:完全平方公式中的交叉项可正可负例题:如果 a2-ka+1 是一个完全平方式,那么 k 的值是________. 分析:当k=2 时,a2-ka+1=a2-2a+1 是一个完全平方
式;当k=-2 时,a2-ka+1=a2+2a+1 也是一个完全平方式.正解:k=2 或-2 失误与防范:错误的原因是没有注意到完全平方公式中的
交叉项可正可负,防范这种错误的方法是牢记公式.易错点 4:二次根式化简时,没注意字母中隐含的负号数,所以化简的结果一定是正数,所以 D 错误.
正解:B失误与防范:错误的原因是没注意字母 a 中隐含的负号,把 a 当成一个正数来计算. 防范这种错误的方法注意字母中隐含的负号,同时注
意中的两个非负性:①被开方数非负;②表示的是一个算
术平方根,是一个非负数.易错点 5:方程两边同时除以一个等于 0 的代数式例题:方程 x(x-1)=x 的根是()A.x=1
C.x1=0,x2=2B.x=2
D.x1=0,x2=1 分析:当x=0 时,方程两边相等,即x=0 是方程的一个
根;当 x≠0 时,原方程同时除以 x,得x-1=1,即x=2.
正解:C
失误与防范:错误的原因是方程两边同时除以 x,忽略 x
可能为 0,这时就造成了失根.防范这种错误的方法是解方程
时,如果方程的两边同时除以一个代数式,一定要注意它是否
会等于 0. 易错点6:确定不等式组的解集时,要注意其中的字母是
否可以等于边界值例题:已知不等式组3+2x≥1,
x-a<0无解,则 a 的取值范围是________.
分析:由不等式3+2x≥1,得x≥-1,由不等式x-a<0,
得 x<a,依据不等式组解集的确定法则确定 a 的值.
正解:a≤-1失误与防范:错误的原因是在确定x≥-1,
x
错误的方法是确定不等式组的解集时要注意其中的字母是否可
以取边界值. 易错点7:注意变化规律中的细节,得出准确的函数图象.
例题:如图 G-2,已知等腰梯形 AOCD,AD∥OC,若动直
线 l 垂直于 OC,且向右平移,设扫过的阴影部分的面积为 S,)OP 为 x,则 S 关于 x 的函数图象大致是(
图 G-2ABCD 分析:分三段考虑:①当直线 l 经过OA 段时,阴影部分的
面积越来越大,并且增大的速度越来越快;②直线 l 经过DC
段时,阴影部分的面积越来越大,并且增大的速度保持不变;
③直线 l 经过DC 段时,阴影部分的面积越来越大,并且增大
的速度越来越小.故选A.
正解:A 失误与防范:错误的原因是忽略对阴影部分的面积增加的
速度进行细节分析,从而选择错误的选项 C.防范这种错误的方
法是仔细观察图形的变化细节,才能更准确地得出函数图象的
变化特点.例题:反比例函数 y=—,当 x≤3 时,y 的取值范围是(C.y≥—或 y<0易错点 8:注意反比例函数的图象有两支2
x)A.y≤2
3B.y≥2
32
3D.0
点与系数 a,b,c 的关系
例题:已知二次函数 y=ax2+bx+c 的图象如图 G-3,对称
轴是直线 x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac)图 G-3<0;④4a+2b+c>0.其中正确的是(
A.①③
B.只有②
C.②④
D.③④
正解:C 失误与防范:错误的原因:二次函数y=ax2+bx+c(a≠0)
的图象特点与系数a,b,c 的关系不是很熟悉,特别容易因为
一个符号的错误造成整个题目的错误.防范这种错误的方法:
记住:①a 的符号决定抛物线的开口方向;②a,b 的符号共同
决定对称轴的位置.a,b 同号对称轴在 y 轴的左侧,a,b 异号
对称轴在y 轴的右侧;③c的符号决定抛物线与 y 轴的交点(0,
c)的位置,c>0 交点在y 轴的正半轴,c<0 交点在 y 轴的负半轴.易错点10:对平行线判定不准确)例题:如图 G-4,在下列条件中,能判断 AD∥BC 的是(
A.∠DAC=∠BCA
B.∠DCB+∠ABC=180°
C.∠ABD=∠BDCD.∠BAC=∠ACD图 G-4 分析:∠DAC 和∠BCA 是直线 AD 和直线 BC 被 AC 所截
形成的内错角,又∵∠DAC=∠BCA,∴AD∥BC.
正解:A 失误与防范:关键是判断选项中两个角是不是直线 AD,
BC 被第三条直线所截形成的两角(同位角、内错角、同旁内角),
再观察是不是符合 AD∥BC 的判定方法. 易错点 11:涉及等腰三角形的高时出现的漏解
例题:等腰三角形一腰上的高与另一腰所成的夹角为 45°,
求这个等腰三角形的顶角的度数.
分析:容易出现漏解.如图G-5(1),因为 CD 是腰AB 边上
的高,且∠ACD=45°,则这个等腰三角形的顶角为45°.(1)(2)图G-5正解:依题意可画出图 G-5(1)(2)两种情形,显然,易求得图(1)中的顶角为 45°和(2)中的顶角为135°. 失误与防范:三角形的高是由三角形的形状所决定的.对
于等腰三角形,当顶角是锐角时,腰上的高在三角形内;当顶
角是钝角时,腰上的高在三角形外.所以应分两种情况进行讨
论. 易错点 12:对平行四边形的判定方法把握不准导致漏解
例题:四边形 ABCD 中,对角线 AC,BD 相交于点 O,给
出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB
=OD.
从中任选两个条件,能使四边形 ABCD 为平行四边形的选法有()A.3 种
C.5 种B.4 种
D.6 种 分析:从一组对边平行且相等(①②),对角线互相平分(③
④),以及条件组合(①③、①④),通过判定三角形全等进一步
判定四边形为平行四边形,仅仅满足条件②③或者是②④不能
证明三角形全等,故选法有 4 种.正解:B易错点13:概念不清,审题不到位导致推理不严密 例题:如图G-6,在菱形ABCD 中,对角线 AC 和 BD 相交
于点 O,OE⊥AB 于点 E,OF⊥BC 于点 F,OG⊥CD 于点 G,
OH⊥AD于点 H,依次连接 EF,FG,GH,HE,试说明四边形
EFGH 为矩形.图 G-6正解:因为OG⊥CD,AB∥CD,所以 OG⊥AB.又OE⊥AB,由垂直公理,得直线OE 和OG 为同一条直线,则E,O,G 三点共线.从而EG 为四边形EFGH 的对角线.同理,可得FH 也是四边形EFGH 的对角线.
因为BD为菱形ABCD 的对角线,
所以∠ABD=∠CBD.又因为OE⊥AB,OF⊥BC,由角平分线性质定理,可得 OE=OF.同理,可得OF=OG,OG=OH,OH=OE.
即OE=OF=OG=OH.所以四边形 EFGH 为平行四边形.因为 OE+OG=OF+OH,即 EG=FH.
所以四边形 EFGH 为矩形. 失误与防范:本题估计很多同学会先说明四边形EFGH 的
“对角线EG 和FH 互相平分”,可得四边形EFGH 为平行四
边形,再说明“对角线EG=FH”,从而得到结论:四边形EFGH
为矩形.表面上看来似乎推理严谨,无懈可击,其实不然.解
本题的关键是说明E,O,G 和 F,O,H 分别是同一条直线上
的三点(也就是三点共线). 易错点14:概念模糊
例题:已知在四边形 ABCD 中,AB =DC ,AC =BD ,
AD≠BC,试说明四边形 ABCD 是等腰梯形.
正解:如图G-7,过点D 作 DE∥AC,交BC 的延长线于点 E,图G-7在△ABC 和△DCB 中,
AB=DC,AC=DB,BC=CB,
所以△ABC≌△DCB.所以∠ACB=∠DBC.
因为DE ∥ AC,所以∠DEC=∠ACB=∠DBC.
所以DE=DB=AC.因为DE ∥ AC,DE=AC,所以四边形ACED 为平行四边形.
所以AD ∥ CE,即AD ∥ BC.因为AD≠BC,所以延长BA,CD 必相交.
所以AB 与DC 不平行.四边形ABCD 的一组对边AD,BC 平行,而另一组对边AB与 DC 不平行,所以四边形ABCD 为梯形.又因为AB=DC,所以四边形ABCD 为等腰梯形. 失误与防范:由于概念模糊,根据一组对边平行,就认定
这个四边形是梯形,这是不正确的.因为满足这个条件的四边
形既可能是梯形,也可能是平行四边形.因此还须说明这个四
边形的另一组对边不平行. 易错点 15:一条弦所对圆周角的值有两个
例题:在半径为 R 的圆内,求长为 R 的弦所对的圆周角.
正解:如图G-8,当圆周角的顶点在优弧上时,⊙O 的半
径为R,AB=R,∠ACB 为弦AB 所对的圆周角,连接OA,OB,
则 OA=OB=AB=R,∴ △OAB 为等边三角形.
1
2图G-8图G-9∴∠AOB=60°,∴∠ACB=—∠AOB=30°.如图G-9,当长为 R 的弦AB 所对的圆周角的顶点在劣弧AB 上时,连接OA,OB,同理可得△OAB 为等边三角形,
∴∠AOB=60°.∴优弧AMB 所对的圆心角为360°-60°=300°.
∴优弧AMB 所对的圆周角∠ACB=150°.
∴长为R 的弦所对的圆周角为30°或150°. 失误与防范:产生错解的原因是只考虑了长为 R 的弦所对
的圆周角的顶点在优弧上,而忽略了圆周角的顶点在劣弧上的
情况.易错点16:误认为若圆与线段只有一个公共点,则圆与线段相切 例题:如图G-10,在Rt△ABC中,∠C=90°,AC=3,BC
=4,若以 C 为圆心,R 为半径的圆与斜边只有一个公共点,则
R 的取值范围是______________________________.图 G-10 正解:①如图G-11,以C为圆心,R为半径的圆与斜边AB
相切.图G-11图 G-12AC·BC 3×4 12∴R=CD=AB 5 5= = =2.4. ②如图 G-12 所示,以点 C 为圆心,R 为半径的圆与斜边
AB 相交于一点,那么 R 应满足 AC<R≤ BC,即 3<R≤ 4.所以当 R=2.4 或 3<R≤4 时,圆与线段只有一个公共点. 失误与防范:产生错解的原因是误认为圆与斜边只有一个
公共点与圆与斜边相切等价,本题圆与斜边只有一个公共点分
两种情况:斜边与圆相切和线段与圆相交,都只有一个公共点.易错点 17:三视图中虚实线意义不明
例题:如图 G-13,正方体表面上画有一圈黑色线条,则它的左视图是()图 G-13ABCD正解:B 失误与防范:正方体中左边的虚线表示在观察时看不到的
轮廓线,而在它的左视图中是可见的实线,故在画左视图中应
画成实线.易错点18:应用性质解题时出现的错误
例题:如图G-14,在△ABC中,DE∥BC, S△ADE:S梯形BCED=1∶3,求 AD∶DB 的值.图 G-14 失误与防范:(1)相似三角形的面积比等于相似比的平方;
(2)由面积求相似比时,是开方求算术平方根,而不是平方.-x+2 x2-4易错点19:不清楚分式的基本性质致误例题:化简分式2 x-6. 失误与防范:分式的化简容易与解分式方程混淆,方式方
程根据等式的基本性质,需要去分母进行化简,分式的化简只
能通分和约分,不能随便去分母,解题时注意每一步过程都有
据可依,就不会出错.易错点20:不清楚分式有意义和除式有意义的条件致误三个数中选一个合适的,代入求值. 失误与防范:解分式化简后代入求值问题时,必须把即将
代入的值先代入原式,检查原式是否有意义.本题中要求分式
同课章节目录
