第七章 观察、猜想与证明 期末试题选编 (含解析)2021-2022学年北京市各地京改版数学七年级下册
文档属性
| 名称 | 第七章 观察、猜想与证明 期末试题选编 (含解析)2021-2022学年北京市各地京改版数学七年级下册 |  | |
| 格式 | zip | ||
| 文件大小 | 840.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 13:17:39 | ||
图片预览


文档简介
第七章 观察、猜想与证明
一、单选题
1.(2022春·北京海淀·七年级统考期末)下列命题是真命题的是( )
A.同位角相等 B.内错角相等 C.同旁内角互补 D.邻补角互补
2.(2022春·北京朝阳·七年级统考期末)下列图形中,∠1和∠2是邻补角的是( )
A. B. C. D.
3.(2022春·北京延庆·七年级统考期末)如图,点O在直线CD上,OB⊥OA.若∠BOD=110°,则∠AOC的度数为( )
A.10° B.20°
C.60° D.70°
4.(2022春·北京顺义·七年级统考期末)如图,∠AOB=50° ,则∠AOB的余角的度数是( )
A.40° B.50° C.130° D.140°
5.(2022春·北京房山·七年级统考期末)若,则的对顶角的大小为( )
A.40° B.50° C.130° D.140°
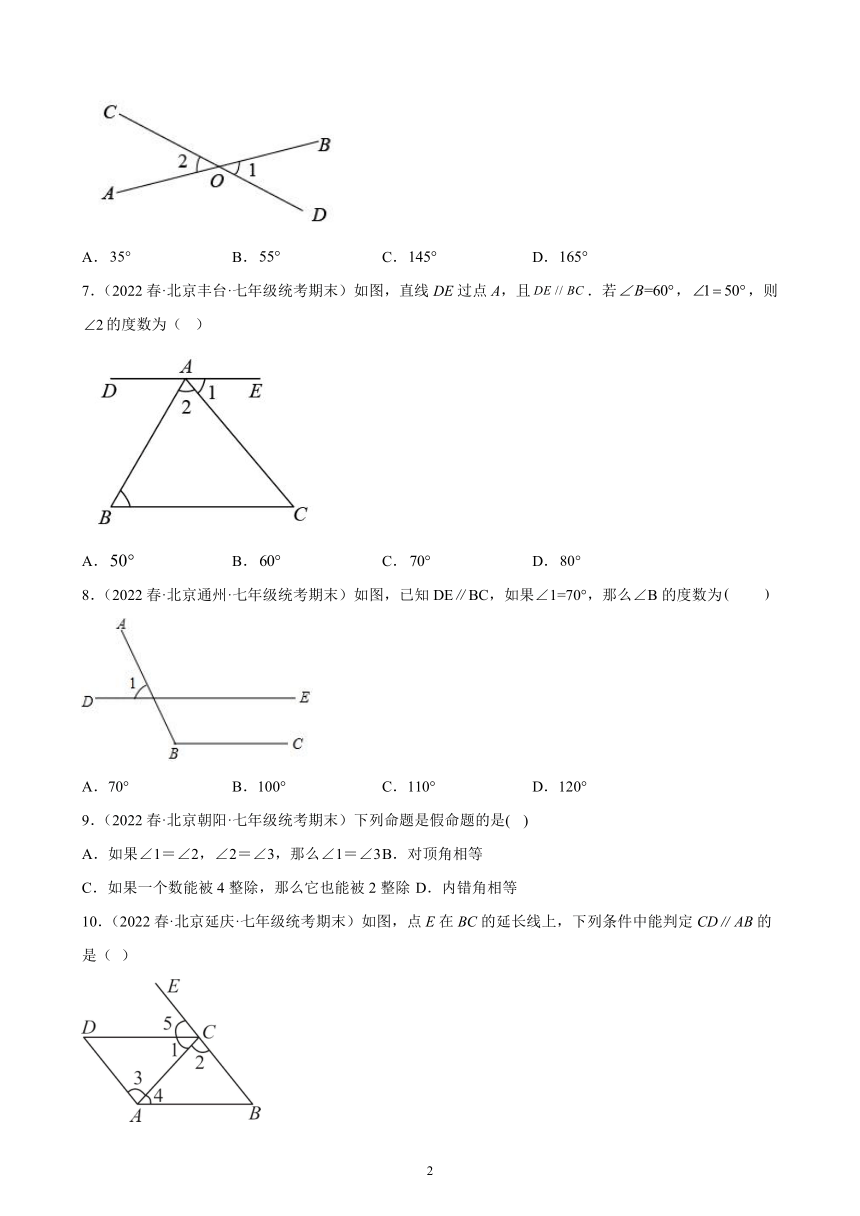
6.(2022春·北京延庆·七年级统考期末)如图,直线AB,CD相交于点O,如果∠1=35°,那么∠2的度数是( )
A. B. C. D.
7.(2022春·北京丰台·七年级统考期末)如图,直线DE过点A,且.若,,则的度数为( )
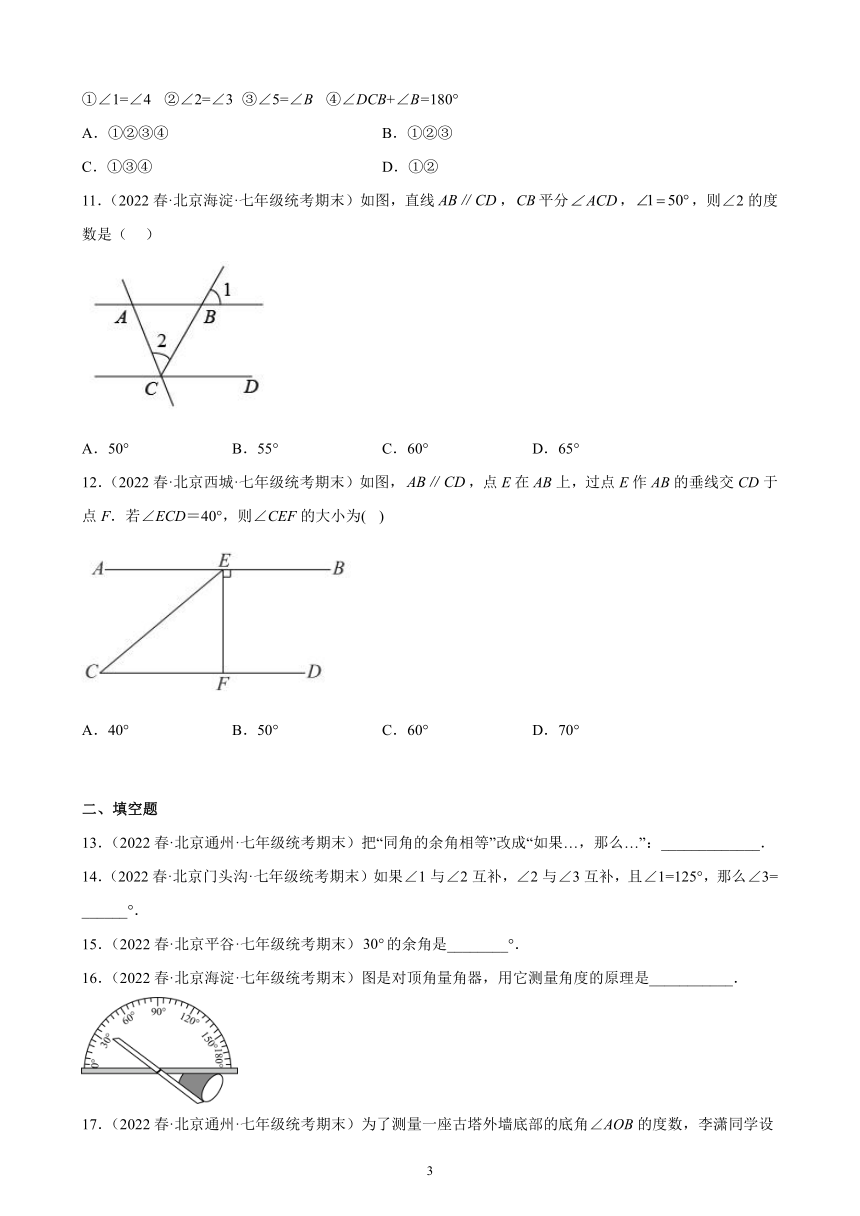
A. B. C. D.
8.(2022春·北京通州·七年级统考期末)如图,已知DE∥BC,如果∠1=70°,那么∠B的度数为
A.70° B.100° C.110° D.120°
9.(2022春·北京朝阳·七年级统考期末)下列命题是假命题的是( )
A.如果∠1=∠2,∠2=∠3,那么∠1=∠3 B.对顶角相等
C.如果一个数能被4整除,那么它也能被2整除 D.内错角相等
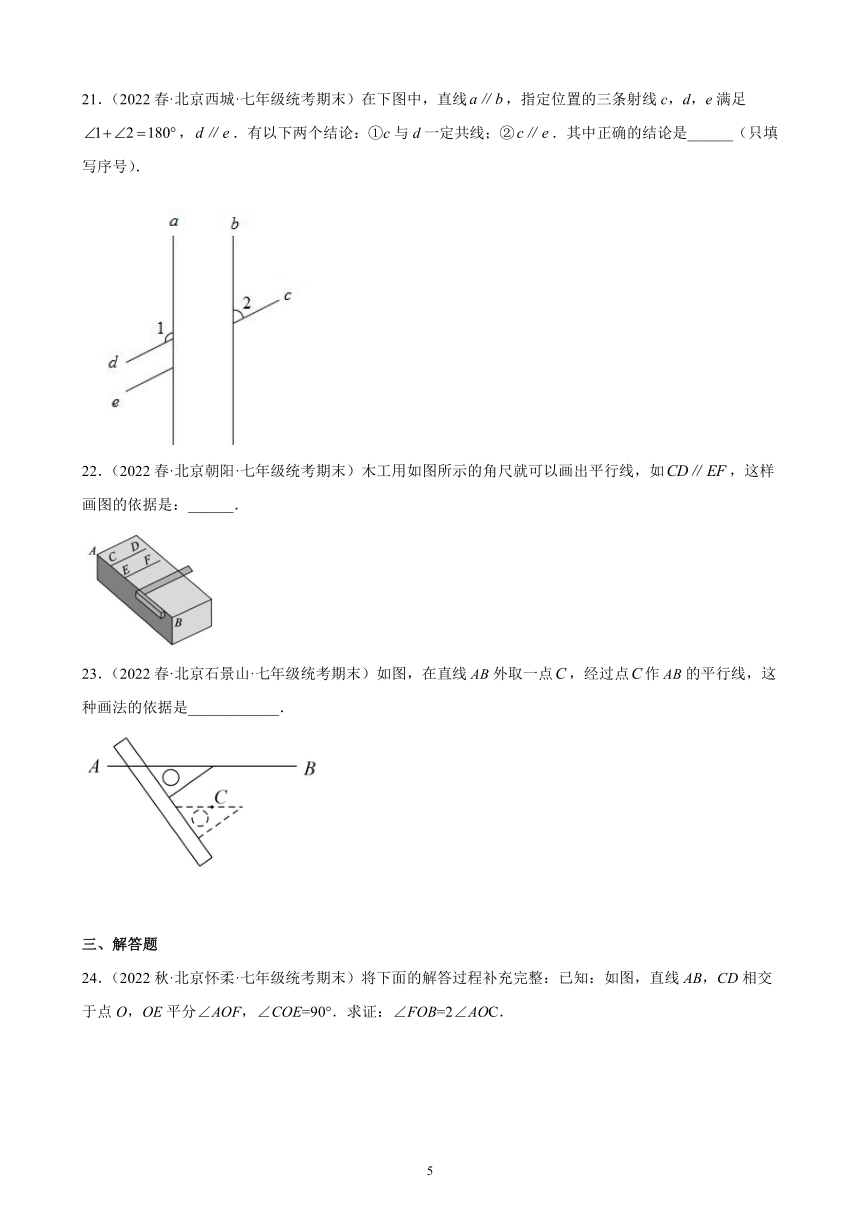
10.(2022春·北京延庆·七年级统考期末)如图,点E在BC的延长线上,下列条件中能判定CDAB的是( )
①∠1=∠4 ②∠2=∠3 ③∠5=∠B ④∠DCB+∠B=180°
A.①②③④ B.①②③
C.①③④ D.①②
11.(2022春·北京海淀·七年级统考期末)如图,直线,平分,,则∠2的度数是( )
A.50° B.55° C.60° D.65°
12.(2022春·北京西城·七年级统考期末)如图,,点E在AB上,过点E作AB的垂线交CD于点F.若∠ECD=40°,则∠CEF的大小为( )
A.40° B.50° C.60° D.70°
二、填空题
13.(2022春·北京通州·七年级统考期末)把“同角的余角相等”改成“如果…,那么…”:_____________.
14.(2022春·北京门头沟·七年级统考期末)如果∠1与∠2互补,∠2与∠3互补,且∠1=125°,那么∠3= ______°.
15.(2022春·北京平谷·七年级统考期末)的余角是________°.
16.(2022春·北京海淀·七年级统考期末)图是对顶角量角器,用它测量角度的原理是___________.
17.(2022春·北京通州·七年级统考期末)为了测量一座古塔外墙底部的底角∠AOB的度数,李潇同学设计了如下测量方案:作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是_______________.
18.(2022春·北京延庆·七年级统考期末)已知:在同一平面内,三条直线a,b,c.下列四个命题为真命题的是_____________.(填写所有真命题的序号)
①如果ab,,那么; ②如果,,那么;
③如果ab,cb,那么ac; ④如果,,那么bc.
19.(2022春·北京丰台·七年级统考期末)如图,点C在射线BD上,请你添加一个条件_____,使得AB∥CE.
20.(2022春·北京海淀·七年级统考期末)埃拉托斯特尼是古希腊著名的地理学家,他曾巧妙估算出地球的周长.如图,处是塞尼城中的一口深井,夏至日中午12时,太阳光可直射井底.处为亚历山大城,它与塞尼城几乎司一条经线上,两地距离约为800km,于是地球周长可近似为,太阳光线看作平行光线,他在亚历山大城测得天顶方向与太阳光线的夹角为7.2°.根据可以推导出的大小,依据是_____________________;埃拉托斯特尼估算得到的地球周长约为___________km.
21.(2022春·北京西城·七年级统考期末)在下图中,直线,指定位置的三条射线c,d,e满足,.有以下两个结论:①c与d一定共线;②.其中正确的结论是______(只填写序号).
22.(2022春·北京朝阳·七年级统考期末)木工用如图所示的角尺就可以画出平行线,如,这样画图的依据是:______.
23.(2022春·北京石景山·七年级统考期末)如图,在直线外取一点,经过点作的平行线,这种画法的依据是____________.
三、解答题
24.(2022秋·北京怀柔·七年级统考期末)将下面的解答过程补充完整:已知:如图,直线AB,CD相交于点O,OE平分∠AOF,∠COE=90°.求证:∠FOB=2∠AOC.
证明:因为OE平分∠AOF,所以∠AOE=∠EOF.( )
因为∠COE=90°,
所以∠AOC+∠AOE=90°
因为直线AB,CD相交于点O.
所以∠EOD=180°-∠COE=90°
所以.∠EOF+∠FOD=90°.
所以∠AOC=_ ___.( )
因为直线AB,CD相交于O,
所以 .( )
所以∠FOB=∠FOD+∠BOD=2∠AOC
25.(2022春·北京石景山·七年级统考期末)如图,点、、、在一条直线上,与交于点,,,求证:
26.(2022春·北京延庆·七年级统考期末)如图,∠B+∠BAD=180°,∠1=∠2. 求证:ABCD.请将下面的证明过程补充完整.
证明:
∵∠B+∠BAD=180°(已知),
∠1+∠BAD=180°( ),
∴∠1=∠B( ).
∵∠1=∠2(已知),
∴∠2= ( ).
∴ABCD( ).
27.(2022春·北京海淀·七年级统考期末)下图所示的格线彼此平行.小明在格线中作已知角,探究角的两边与格线形成的锐角所满足的数量关系.他先作出,
(1)①如图1,点在一条格线上,当∠1=20°时,∠2=________°;
②如图2,点在两条格线之间,用等式表示∠1与∠2之间的数量关系,并证明;
(2)在图3中,小明作射线,使得.记与图中一条格线形成的锐角为,与图中另一条格线形成的锐角为,请直接用等式表示α与B之间的数量关系.
28.(2022春·北京东城·七年级统考期末)如图,直线与直线,分别交于点,,是它的补角的3倍,.判断与的位置关系,并说明理由.
29.(2022春·北京丰台·七年级统考期末)补全解题过程.
已知:如图,于点,于点,.
求证:.
证明:∵,,
∴.
∴(______)(填推理依据).
∴(______)(填推理依据).
又∵,
∴.
∴(______)(填推理依据).
30.(2022春·北京海淀·七年级统考期末)如图,已知,于点,.
(1)求证:;
(2)连接,若,且,求的度数.
参考答案:
1.D
【分析】根据同位角、内错角、同旁内角、邻补角的定义逐项判断即可得.
【详解】解:A.同位角不一定相等,则此项是假命题,不符题意;
B.内错角不一定相等,则此项是假命题,不符题意;
C.同旁内角不一定互补,则此项是假命题,不符题意;
D.邻补角互补,则此项是真命题,符合题意;
故选:D.
【点睛】本题考查了同位角、内错角、同旁内角、邻补角、命题,熟记各概念是解题关键.
2.B
【分析】根据邻补角的概念进行判定即可得出答案.
【详解】解:A.与是对顶角,故选项不符合题意;
B.与是邻补角,故选项符合题意;
C.与不存在公共边,不是邻补角,故选项不符合题意;
D.与是同旁内角,故选项不符合题意;
故选:B.
【点睛】本题主要考查的是邻补角的定义,熟练掌握邻补角的定义是解题的关键.
3.B
【分析】利用互余的角的关系和邻补角的关系进行计算即可.
【详解】解:∵∠BOD=110°,
∴∠BOC=180°-110°=70°,
∵OB⊥OA,
∴∠AOB=90°,
∴∠AOC=90°-∠BOC=90°-70°=20°,
故选:B.
【点睛】本题考查的是互余两角、邻补角的定义,解题的关键是找准互余的两角和互补的两角.
4.A
【分析】根据互余的两个角和为90°解答即可.
【详解】解:因为互余的两个角和为90°,
所以∠AOB的余角的度数为90°-50°=40°.
故选:A.
【点睛】此题考查的是余角的性质,掌握互余的两个角和为90°是解题的关键.
5.B
【分析】根据对顶角相等直接可得答案.
【详解】解:∵,
∴的对顶角的大小为
故选B
【点睛】本题考查的是对顶角的性质,掌握“对顶角相等”是解本题的关键.
6.A
【分析】根据对顶角的性质解答 .
【详解】解:由对顶角的性质可得:∠1=∠2,
∵∠1=35°,
∴∠2=35°,
故选A.
【点睛】本题考查对顶角的应用,熟练掌握对顶角的性质是解题关键 .
7.C
【分析】根据两直线平行同旁内角互补求出∠BAE,即可求出∠2.
【详解】∵,
∴,
∴,
即:,
∴,
故选:C.
【点睛】本题考查平行线的性质,熟记平行线的基本性质是解题关键.
8.C
【分析】根据平行线的性质可知∠B与∠2互补,再根据对顶角的性质可知∠2=∠1=70°,据此即可得答案.
【详解】解:如图,
∵DE//BC,
∴∠2+∠B=180°,
∵∠2=∠1=70°,
∴∠B=180°-70°=110°,
故选C.
【点睛】本题考查了平行线的性质、对顶角的性质,熟练掌握平行线的性质是解题的关键.
9.D
【分析】利用对顶角的性质、实数的性质、平行线的性质分别判断后即可确定正确的选项.
【详解】解:A、如果,,那么,正确,是真命题,不符合题意;
B、对顶角相等,正确,是真命题,不符合题意;
C、如果一个数能被4整除,那么它也能被2整除,正确,是真命题,不符合题意;
D、两直线平行,内错角相等,故原命题错误,是假命题,符合题意.
故选:D.
【点睛】本题考查了命题与定理的知识,解题的关键是了解对顶角的性质、实数的性质、平行线的性质,难度不大.
10.C
【分析】根据平行线的判定方法对① ② ③④每一选项的正确性进行判断即可得到解答 .
【详解】解:因为∠1和∠4是内错角,所以由∠1=∠4 可以得到CD ∥ AB,①正确;
因为∠2和∠3是DA与CB的内错角,不是CD 与 AB的内错角,所以由∠2=∠3不能得到CD ∥ AB,②错误;
因为∠5和∠B是同位角,所以由∠5=∠B可以得到CD ∥ AB,③正确;
因为∠DCB和∠B是同旁内角,所以由∠DCB+∠B=180°可以得到CD ∥ AB,④正确;
故选:C.
【点睛】本题考查平行线的应用,熟练掌握平行线的判定方法是解题关键.
11.A
【分析】先根据平行线的性质可得,再根据角平分线的定义即可得.
【详解】解:,
,
平分,
,
故选:A.
【点睛】本题考查了平行线的性质、角平分线,熟练掌握平行线的性质是解题关键.
12.B
【分析】由垂直可得∠AEF=90°,再由平行线的性质得∠AEC=∠ECD=40°,从而可求∠CEF的度数.
【详解】解:∵过点E作AB的垂线交CD于点F,
∴∠AEF=90°,
∵AB∥CD,∠ECD=40°,
∴∠AEC=∠ECD=40°,
∴∠CEF=∠AEF-∠AEC=50°.
故选:B.
【点睛】本题主要考查平行线的性质,解答的关键是熟记平行线的性质并灵活运用.
13.如果两个角是同一个角的余角,那么这两个角相等
【分析】找到命题的条件和结论进行改写即可.
【详解】根据命题的特点,可以改写为:“如果两个角是同一个角的余角,那么这两个角相等”
故答案为:如果两个角是同一个角的余角,那么这两个角相等.
【点睛】本题考查了命题的特点,解题的关键是“如果”后面接题设,“那么”后面接结论.
14.125
【分析】由于∠1、∠3都与∠2互补,应当联想到用“同角的补角相等”来解决.
【详解】∵∠1与∠2互补,∠2与∠3互补,
∴∠1+∠2=180°,∠2+∠3=180°,
∴∠3=∠1=125°.
故答案为:125.
【点睛】本题考查同角的补角相等,解此题时要认真观察,只要发现∠1、∠3都与∠2互补,即可大功告成.
15.
【分析】从余角的定义出发:两个角和为,则这两个角互余;由此可得解.
【详解】解:由两个角和为,则这两个角互余可得:
故答案为.
【点睛】本题考查余角的定义;关键在于知道两个角和为,则这两个角互余.
16.对顶角相等
【分析】由题意得,扇形零件的圆心角与其两边的反向延长线组的角是对顶角,根据对顶角的性质解答即可.
【详解】解:由题意得,扇形零件的圆心角与其两边的反向延长线组的角是对顶角.
因为对顶角相等,
所以利用图中的量角器可以量出这个扇形零件的圆心角的度数.
故答案为对顶角相等.
【点睛】本题考查了对顶角的性质,正确掌握对顶角的性质是解题的关键.
17.对顶角相等
【分析】由对顶角相等即可得出结论.
【详解】这个测量方案的依据是:对顶角相等;
故答案是:对顶角相等.
【点睛】本题考查的是对顶角相等的性质和作图;根据题意正确作出图形、设计出测量方案是解题的关键.
18.①③④
【分析】分别根据每种情况画出符合条件的图形,再结合垂直的定义,平行线的判定逐一判断即可.
【详解】解:如图,ab,,
则,故①符合题意;
如图,,,
则 故②不符合题意;④符合题意;
如图,ab,cb,
则ac;故③符合题意;
故答案为:①③④
【点睛】本题考查的是平面内直线与直线的位置关系,平行线的性质,垂直的定义,命题真假的判断,掌握“平行公理,平面内垂直于同一直线的两直线平行”是解本题的关键.
19.∠B=∠ECD(答案不唯一)
【详解】解:当∠B=∠ECD时,AB∥CE;
当∠B+∠BCE=180°时,AB∥CE;
当∠A=∠ACE时,AB∥CE.
故答案为∠B=∠ECD(答案不唯一).
【点睛】本题主要考查平行线的判定,熟练掌握平行线的判定定理是解题的关键.
20. 两直线平行,同位角相等 40000
【分析】根据太阳光线互为平行线,则亚历山大城、赛尼城与地球中心所成角和天顶方向与太阳光线的夹角为同位角,利用两直线平行,同位角相等求出,再代入计算求解.
【详解】解:由题意知,太阳光线互为平行线,则亚历山大城、赛尼城与地球中心所成角和天顶方向与太阳光线的夹角为同位角,
则亚历山大城、赛伊尼与地球中心所成角为=7.2°,
理由是两直线平行,同位角相等.
因为亚历山大城、赛尼城间距离为800km,
所以地球周长为km.
故答案为:两直线平行,同位角相等;40000.
【点睛】本题主要考查了平行线的性质,有理数的乘除运算,确定出=7.2°是解答关键.
21.②
【分析】根据平行线的性质对各结论进行分析即可.
【详解】解:如图,延长射线c交直线a于点A,直线b于点C,
①∵a∥b,
∴∠2=∠CAD,
∵∠CAD+∠BAD=180°,∠1+∠2=180°,
∴∠BAD=∠1,
∴c∥d,故①结论错误;
②∵d∥e,c∥d,
∴c∥e,故②结论正确.
故答案为:②.
【点睛】本题主要考查平行线的性质,解答的关键是熟记平行线的性质并灵活运用.
22.同位角相等,两直线平行
【分析】根据平行线的判定,同位角相等,两直线平行作答.
【详解】解:木工用角尺画出,其依据是同位角相等,两直线平行,
故答案为:同位角相等,两直线平行.
【点睛】此题主要考查了平行线的判定,正确掌握平行线的判定方法是解题关键.
23.同位角相等,两直线平行
【分析】根据画法得到同位角相等,然后根据平行线的判定方法可得到经过点C的直线与AB平行.
【详解】解:如图,
由图形痕迹可得∠BDE=∠CEF,则根据同位角相等,两直线平行可判断经过点C的直线与AB平行.
故答案为:同位角相等,两直线平行.
【点睛】本题考查了作图一复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行线的判定.
24.角平分线的定义; ;等角的余角相等;∠BOD=∠AOC;对顶角相等
【分析】根据题目提供的解析过程结合具体问题进行解答即可.
【详解】证明:∵OE平分∠AOF,
∴∠AOE=∠EOF,(角平分线的定义)
∵∠COE=90°,
∴∠AOC+∠AOE=90°,
∵直线AB,CD相交于点O,
∴∠EOD=180°-∠COE=90°,
∴∠EOF+∠FOD=90°,
∴∠AOC=∠FOD(等角的余角相等)
∵直线AB,CD相交于O,
∴∠BOD=∠AOC,(对顶角相等)
∴∠FOB=∠FOD+∠BOD=2∠AOC.
故答案为:角平分线的定义;;等角的余角相等;∠BOD=∠AOC;对顶角相等.
【点睛】本题主要考查了角平分线的定义,对顶角,邻补角,熟练掌握同角或等角的余角相等是解题的关键.
25.证明见解析
【分析】根据同位角相等,两直线平行可得AE//BF,进而可得∠E=∠2,由CE//DF可得∠F=∠2,最后根据等量代换即可证明结论.
【详解】∵,
∴,
∴.
∵CE//DF,
∴.
∴.
【点睛】本题考查了平行线的判定与性质,熟练掌握平行线的判定定理与性质定理是解题的关键.
26.见解析
【分析】根据平行的判定定理证明即可.
【详解】∵∠B+∠BAD=180°(已知),
∠1+∠BAD=180°(平角定义),
∴∠1=∠B(同角的补角相等).
∵∠1=∠2(已知),
∴∠2=∠B(等量代换).
∴ABCD(同位角相等,两条直线平行).
【点睛】本题考查平行线的判定定理,解题的关键是掌握平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
27.(1)①40;②∠1+∠2=60°,证明见解析;
(2)α+β=105°或α-β=15°
【分析】(1)①先标出∠3和∠4,然后再根据平行的性质可得∠1=∠3,∠2=∠4,然后再利用角的和差解答即可;
②如图:过点C作一条直线平行于格线,标出∠3和∠4 ,再根据平行的性质可得∠1=∠3,∠2=∠4,然后再利用角和差解答即可;
(2)分两种情况:当射线OC在∠AOB的内部,当射线OC在∠AOB的外部,然后利用平行线的性质和三角形的外角的性质进行计算,即可解答.
(1)
解:①如图1:标出∠3和∠4
由格线平行,利用平行的性质可得:∠1=∠3,∠2=∠4
∵∠3+∠4=∠AOB=60°,∠1=20°
∴∠1+∠2=60°
∴∠2=60°-20°=40°
故答案为:40;
②∠1+∠2=60°,证明如下:
证明:如图:过点C作一条直线平行于格线,标出∠3和∠4
由格线平行可得∠1=∠3,∠2=∠4
∵∠3+∠4=∠AOB=60°
∴∠1+∠2=60°.
(2)
解:设OA与图中一条格线形成的锐角为,OC与另一条格线形成的锐角为
当射线OC在∠AOB的内部,如图:
在图中随意选择两条格线标出、且过O点作平行于格线的辅助线,并标出∠1和∠2
由格线平行可得∠2=,∠1+∠2=
∵∠AOB=60°,∠COB=45°
∴∠AOC=15°即∠1=15°,∠1+=
∴=15°+
即
当射线OC在∠AOB的外部,如图:
∵∠COB=45°,∠AOB=60°
∴∠AOC=∠AOB+∠COB=105°
由(1)中②知,∠AOC=α+β
∴α+β=105°
综上所述:α+β=105°或α-β=15°.
【点睛】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.难点是作辅助线,第(2)要分类讨论,不要出现遗漏情况.
28.;理由见解析
【分析】先根据补角的定义求出的度数,然后求出∠CFE和∠2的度数,最后根据平行线的判定进行解答即可.
【详解】解:;理由如下:
∵是它的补角的3倍,
∴设,则的补角为,
∴,
解得:,
∴,
∴,
∵,
∴,
∴,
∴.
【点睛】本题主要考查了补角的有关计算,平行线的判定,根据题意求出,是解题的关键.
29.;同位角相等,两直线平行;;两直线平行,同位角相等;;内错角相等,两直线平行
【分析】先证明,可得,再证明,从而可得结论.
【详解】证明:∵,,
∴.
∴(同位角相等,两直线平行).
∴(两直线平行,同位角相等).
又∵,
∴.
∴(内错角相等,两直线平行).
【点睛】本题考查的是平行线的性质与判定,掌握“平行线的性质与平行线的判定方法以及简单的逻辑思维推理”是解本题的关键.
30.(1)证明见解析
(2)
【分析】(1)先根据垂直的定义可得,再根据平行线的判定可得,然后根据平行线的性质可得,从而可得,最后根据平行线的判定即可得证;
(2)连接,设,则,再根据建立方程,解方程可得,然后根据平行线的性质即可得.
(1)
证明:,
,
,
,
,
,
,
,
.
(2)
解:如图,连接,
设,
,
,
,
由(1)已得:,
,
,
解得,
即,
由(1)已证:,
.
【点睛】本题考查了平行线的判定与性质、垂直等知识点,熟练掌握平行线的判定与性质是解题关键.
一、单选题
1.(2022春·北京海淀·七年级统考期末)下列命题是真命题的是( )
A.同位角相等 B.内错角相等 C.同旁内角互补 D.邻补角互补
2.(2022春·北京朝阳·七年级统考期末)下列图形中,∠1和∠2是邻补角的是( )
A. B. C. D.
3.(2022春·北京延庆·七年级统考期末)如图,点O在直线CD上,OB⊥OA.若∠BOD=110°,则∠AOC的度数为( )
A.10° B.20°
C.60° D.70°
4.(2022春·北京顺义·七年级统考期末)如图,∠AOB=50° ,则∠AOB的余角的度数是( )
A.40° B.50° C.130° D.140°
5.(2022春·北京房山·七年级统考期末)若,则的对顶角的大小为( )
A.40° B.50° C.130° D.140°
6.(2022春·北京延庆·七年级统考期末)如图,直线AB,CD相交于点O,如果∠1=35°,那么∠2的度数是( )
A. B. C. D.
7.(2022春·北京丰台·七年级统考期末)如图,直线DE过点A,且.若,,则的度数为( )
A. B. C. D.
8.(2022春·北京通州·七年级统考期末)如图,已知DE∥BC,如果∠1=70°,那么∠B的度数为
A.70° B.100° C.110° D.120°
9.(2022春·北京朝阳·七年级统考期末)下列命题是假命题的是( )
A.如果∠1=∠2,∠2=∠3,那么∠1=∠3 B.对顶角相等
C.如果一个数能被4整除,那么它也能被2整除 D.内错角相等
10.(2022春·北京延庆·七年级统考期末)如图,点E在BC的延长线上,下列条件中能判定CDAB的是( )
①∠1=∠4 ②∠2=∠3 ③∠5=∠B ④∠DCB+∠B=180°
A.①②③④ B.①②③
C.①③④ D.①②
11.(2022春·北京海淀·七年级统考期末)如图,直线,平分,,则∠2的度数是( )
A.50° B.55° C.60° D.65°
12.(2022春·北京西城·七年级统考期末)如图,,点E在AB上,过点E作AB的垂线交CD于点F.若∠ECD=40°,则∠CEF的大小为( )
A.40° B.50° C.60° D.70°
二、填空题
13.(2022春·北京通州·七年级统考期末)把“同角的余角相等”改成“如果…,那么…”:_____________.
14.(2022春·北京门头沟·七年级统考期末)如果∠1与∠2互补,∠2与∠3互补,且∠1=125°,那么∠3= ______°.
15.(2022春·北京平谷·七年级统考期末)的余角是________°.
16.(2022春·北京海淀·七年级统考期末)图是对顶角量角器,用它测量角度的原理是___________.
17.(2022春·北京通州·七年级统考期末)为了测量一座古塔外墙底部的底角∠AOB的度数,李潇同学设计了如下测量方案:作AO,BO的延长线OD,OC,量出∠COD的度数,从而得到∠AOB的度数.这个测量方案的依据是_______________.
18.(2022春·北京延庆·七年级统考期末)已知:在同一平面内,三条直线a,b,c.下列四个命题为真命题的是_____________.(填写所有真命题的序号)
①如果ab,,那么; ②如果,,那么;
③如果ab,cb,那么ac; ④如果,,那么bc.
19.(2022春·北京丰台·七年级统考期末)如图,点C在射线BD上,请你添加一个条件_____,使得AB∥CE.
20.(2022春·北京海淀·七年级统考期末)埃拉托斯特尼是古希腊著名的地理学家,他曾巧妙估算出地球的周长.如图,处是塞尼城中的一口深井,夏至日中午12时,太阳光可直射井底.处为亚历山大城,它与塞尼城几乎司一条经线上,两地距离约为800km,于是地球周长可近似为,太阳光线看作平行光线,他在亚历山大城测得天顶方向与太阳光线的夹角为7.2°.根据可以推导出的大小,依据是_____________________;埃拉托斯特尼估算得到的地球周长约为___________km.
21.(2022春·北京西城·七年级统考期末)在下图中,直线,指定位置的三条射线c,d,e满足,.有以下两个结论:①c与d一定共线;②.其中正确的结论是______(只填写序号).
22.(2022春·北京朝阳·七年级统考期末)木工用如图所示的角尺就可以画出平行线,如,这样画图的依据是:______.
23.(2022春·北京石景山·七年级统考期末)如图,在直线外取一点,经过点作的平行线,这种画法的依据是____________.
三、解答题
24.(2022秋·北京怀柔·七年级统考期末)将下面的解答过程补充完整:已知:如图,直线AB,CD相交于点O,OE平分∠AOF,∠COE=90°.求证:∠FOB=2∠AOC.
证明:因为OE平分∠AOF,所以∠AOE=∠EOF.( )
因为∠COE=90°,
所以∠AOC+∠AOE=90°
因为直线AB,CD相交于点O.
所以∠EOD=180°-∠COE=90°
所以.∠EOF+∠FOD=90°.
所以∠AOC=_ ___.( )
因为直线AB,CD相交于O,
所以 .( )
所以∠FOB=∠FOD+∠BOD=2∠AOC
25.(2022春·北京石景山·七年级统考期末)如图,点、、、在一条直线上,与交于点,,,求证:
26.(2022春·北京延庆·七年级统考期末)如图,∠B+∠BAD=180°,∠1=∠2. 求证:ABCD.请将下面的证明过程补充完整.
证明:
∵∠B+∠BAD=180°(已知),
∠1+∠BAD=180°( ),
∴∠1=∠B( ).
∵∠1=∠2(已知),
∴∠2= ( ).
∴ABCD( ).
27.(2022春·北京海淀·七年级统考期末)下图所示的格线彼此平行.小明在格线中作已知角,探究角的两边与格线形成的锐角所满足的数量关系.他先作出,
(1)①如图1,点在一条格线上,当∠1=20°时,∠2=________°;
②如图2,点在两条格线之间,用等式表示∠1与∠2之间的数量关系,并证明;
(2)在图3中,小明作射线,使得.记与图中一条格线形成的锐角为,与图中另一条格线形成的锐角为,请直接用等式表示α与B之间的数量关系.
28.(2022春·北京东城·七年级统考期末)如图,直线与直线,分别交于点,,是它的补角的3倍,.判断与的位置关系,并说明理由.
29.(2022春·北京丰台·七年级统考期末)补全解题过程.
已知:如图,于点,于点,.
求证:.
证明:∵,,
∴.
∴(______)(填推理依据).
∴(______)(填推理依据).
又∵,
∴.
∴(______)(填推理依据).
30.(2022春·北京海淀·七年级统考期末)如图,已知,于点,.
(1)求证:;
(2)连接,若,且,求的度数.
参考答案:
1.D
【分析】根据同位角、内错角、同旁内角、邻补角的定义逐项判断即可得.
【详解】解:A.同位角不一定相等,则此项是假命题,不符题意;
B.内错角不一定相等,则此项是假命题,不符题意;
C.同旁内角不一定互补,则此项是假命题,不符题意;
D.邻补角互补,则此项是真命题,符合题意;
故选:D.
【点睛】本题考查了同位角、内错角、同旁内角、邻补角、命题,熟记各概念是解题关键.
2.B
【分析】根据邻补角的概念进行判定即可得出答案.
【详解】解:A.与是对顶角,故选项不符合题意;
B.与是邻补角,故选项符合题意;
C.与不存在公共边,不是邻补角,故选项不符合题意;
D.与是同旁内角,故选项不符合题意;
故选:B.
【点睛】本题主要考查的是邻补角的定义,熟练掌握邻补角的定义是解题的关键.
3.B
【分析】利用互余的角的关系和邻补角的关系进行计算即可.
【详解】解:∵∠BOD=110°,
∴∠BOC=180°-110°=70°,
∵OB⊥OA,
∴∠AOB=90°,
∴∠AOC=90°-∠BOC=90°-70°=20°,
故选:B.
【点睛】本题考查的是互余两角、邻补角的定义,解题的关键是找准互余的两角和互补的两角.
4.A
【分析】根据互余的两个角和为90°解答即可.
【详解】解:因为互余的两个角和为90°,
所以∠AOB的余角的度数为90°-50°=40°.
故选:A.
【点睛】此题考查的是余角的性质,掌握互余的两个角和为90°是解题的关键.
5.B
【分析】根据对顶角相等直接可得答案.
【详解】解:∵,
∴的对顶角的大小为
故选B
【点睛】本题考查的是对顶角的性质,掌握“对顶角相等”是解本题的关键.
6.A
【分析】根据对顶角的性质解答 .
【详解】解:由对顶角的性质可得:∠1=∠2,
∵∠1=35°,
∴∠2=35°,
故选A.
【点睛】本题考查对顶角的应用,熟练掌握对顶角的性质是解题关键 .
7.C
【分析】根据两直线平行同旁内角互补求出∠BAE,即可求出∠2.
【详解】∵,
∴,
∴,
即:,
∴,
故选:C.
【点睛】本题考查平行线的性质,熟记平行线的基本性质是解题关键.
8.C
【分析】根据平行线的性质可知∠B与∠2互补,再根据对顶角的性质可知∠2=∠1=70°,据此即可得答案.
【详解】解:如图,
∵DE//BC,
∴∠2+∠B=180°,
∵∠2=∠1=70°,
∴∠B=180°-70°=110°,
故选C.
【点睛】本题考查了平行线的性质、对顶角的性质,熟练掌握平行线的性质是解题的关键.
9.D
【分析】利用对顶角的性质、实数的性质、平行线的性质分别判断后即可确定正确的选项.
【详解】解:A、如果,,那么,正确,是真命题,不符合题意;
B、对顶角相等,正确,是真命题,不符合题意;
C、如果一个数能被4整除,那么它也能被2整除,正确,是真命题,不符合题意;
D、两直线平行,内错角相等,故原命题错误,是假命题,符合题意.
故选:D.
【点睛】本题考查了命题与定理的知识,解题的关键是了解对顶角的性质、实数的性质、平行线的性质,难度不大.
10.C
【分析】根据平行线的判定方法对① ② ③④每一选项的正确性进行判断即可得到解答 .
【详解】解:因为∠1和∠4是内错角,所以由∠1=∠4 可以得到CD ∥ AB,①正确;
因为∠2和∠3是DA与CB的内错角,不是CD 与 AB的内错角,所以由∠2=∠3不能得到CD ∥ AB,②错误;
因为∠5和∠B是同位角,所以由∠5=∠B可以得到CD ∥ AB,③正确;
因为∠DCB和∠B是同旁内角,所以由∠DCB+∠B=180°可以得到CD ∥ AB,④正确;
故选:C.
【点睛】本题考查平行线的应用,熟练掌握平行线的判定方法是解题关键.
11.A
【分析】先根据平行线的性质可得,再根据角平分线的定义即可得.
【详解】解:,
,
平分,
,
故选:A.
【点睛】本题考查了平行线的性质、角平分线,熟练掌握平行线的性质是解题关键.
12.B
【分析】由垂直可得∠AEF=90°,再由平行线的性质得∠AEC=∠ECD=40°,从而可求∠CEF的度数.
【详解】解:∵过点E作AB的垂线交CD于点F,
∴∠AEF=90°,
∵AB∥CD,∠ECD=40°,
∴∠AEC=∠ECD=40°,
∴∠CEF=∠AEF-∠AEC=50°.
故选:B.
【点睛】本题主要考查平行线的性质,解答的关键是熟记平行线的性质并灵活运用.
13.如果两个角是同一个角的余角,那么这两个角相等
【分析】找到命题的条件和结论进行改写即可.
【详解】根据命题的特点,可以改写为:“如果两个角是同一个角的余角,那么这两个角相等”
故答案为:如果两个角是同一个角的余角,那么这两个角相等.
【点睛】本题考查了命题的特点,解题的关键是“如果”后面接题设,“那么”后面接结论.
14.125
【分析】由于∠1、∠3都与∠2互补,应当联想到用“同角的补角相等”来解决.
【详解】∵∠1与∠2互补,∠2与∠3互补,
∴∠1+∠2=180°,∠2+∠3=180°,
∴∠3=∠1=125°.
故答案为:125.
【点睛】本题考查同角的补角相等,解此题时要认真观察,只要发现∠1、∠3都与∠2互补,即可大功告成.
15.
【分析】从余角的定义出发:两个角和为,则这两个角互余;由此可得解.
【详解】解:由两个角和为,则这两个角互余可得:
故答案为.
【点睛】本题考查余角的定义;关键在于知道两个角和为,则这两个角互余.
16.对顶角相等
【分析】由题意得,扇形零件的圆心角与其两边的反向延长线组的角是对顶角,根据对顶角的性质解答即可.
【详解】解:由题意得,扇形零件的圆心角与其两边的反向延长线组的角是对顶角.
因为对顶角相等,
所以利用图中的量角器可以量出这个扇形零件的圆心角的度数.
故答案为对顶角相等.
【点睛】本题考查了对顶角的性质,正确掌握对顶角的性质是解题的关键.
17.对顶角相等
【分析】由对顶角相等即可得出结论.
【详解】这个测量方案的依据是:对顶角相等;
故答案是:对顶角相等.
【点睛】本题考查的是对顶角相等的性质和作图;根据题意正确作出图形、设计出测量方案是解题的关键.
18.①③④
【分析】分别根据每种情况画出符合条件的图形,再结合垂直的定义,平行线的判定逐一判断即可.
【详解】解:如图,ab,,
则,故①符合题意;
如图,,,
则 故②不符合题意;④符合题意;
如图,ab,cb,
则ac;故③符合题意;
故答案为:①③④
【点睛】本题考查的是平面内直线与直线的位置关系,平行线的性质,垂直的定义,命题真假的判断,掌握“平行公理,平面内垂直于同一直线的两直线平行”是解本题的关键.
19.∠B=∠ECD(答案不唯一)
【详解】解:当∠B=∠ECD时,AB∥CE;
当∠B+∠BCE=180°时,AB∥CE;
当∠A=∠ACE时,AB∥CE.
故答案为∠B=∠ECD(答案不唯一).
【点睛】本题主要考查平行线的判定,熟练掌握平行线的判定定理是解题的关键.
20. 两直线平行,同位角相等 40000
【分析】根据太阳光线互为平行线,则亚历山大城、赛尼城与地球中心所成角和天顶方向与太阳光线的夹角为同位角,利用两直线平行,同位角相等求出,再代入计算求解.
【详解】解:由题意知,太阳光线互为平行线,则亚历山大城、赛尼城与地球中心所成角和天顶方向与太阳光线的夹角为同位角,
则亚历山大城、赛伊尼与地球中心所成角为=7.2°,
理由是两直线平行,同位角相等.
因为亚历山大城、赛尼城间距离为800km,
所以地球周长为km.
故答案为:两直线平行,同位角相等;40000.
【点睛】本题主要考查了平行线的性质,有理数的乘除运算,确定出=7.2°是解答关键.
21.②
【分析】根据平行线的性质对各结论进行分析即可.
【详解】解:如图,延长射线c交直线a于点A,直线b于点C,
①∵a∥b,
∴∠2=∠CAD,
∵∠CAD+∠BAD=180°,∠1+∠2=180°,
∴∠BAD=∠1,
∴c∥d,故①结论错误;
②∵d∥e,c∥d,
∴c∥e,故②结论正确.
故答案为:②.
【点睛】本题主要考查平行线的性质,解答的关键是熟记平行线的性质并灵活运用.
22.同位角相等,两直线平行
【分析】根据平行线的判定,同位角相等,两直线平行作答.
【详解】解:木工用角尺画出,其依据是同位角相等,两直线平行,
故答案为:同位角相等,两直线平行.
【点睛】此题主要考查了平行线的判定,正确掌握平行线的判定方法是解题关键.
23.同位角相等,两直线平行
【分析】根据画法得到同位角相等,然后根据平行线的判定方法可得到经过点C的直线与AB平行.
【详解】解:如图,
由图形痕迹可得∠BDE=∠CEF,则根据同位角相等,两直线平行可判断经过点C的直线与AB平行.
故答案为:同位角相等,两直线平行.
【点睛】本题考查了作图一复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了平行线的判定.
24.角平分线的定义; ;等角的余角相等;∠BOD=∠AOC;对顶角相等
【分析】根据题目提供的解析过程结合具体问题进行解答即可.
【详解】证明:∵OE平分∠AOF,
∴∠AOE=∠EOF,(角平分线的定义)
∵∠COE=90°,
∴∠AOC+∠AOE=90°,
∵直线AB,CD相交于点O,
∴∠EOD=180°-∠COE=90°,
∴∠EOF+∠FOD=90°,
∴∠AOC=∠FOD(等角的余角相等)
∵直线AB,CD相交于O,
∴∠BOD=∠AOC,(对顶角相等)
∴∠FOB=∠FOD+∠BOD=2∠AOC.
故答案为:角平分线的定义;;等角的余角相等;∠BOD=∠AOC;对顶角相等.
【点睛】本题主要考查了角平分线的定义,对顶角,邻补角,熟练掌握同角或等角的余角相等是解题的关键.
25.证明见解析
【分析】根据同位角相等,两直线平行可得AE//BF,进而可得∠E=∠2,由CE//DF可得∠F=∠2,最后根据等量代换即可证明结论.
【详解】∵,
∴,
∴.
∵CE//DF,
∴.
∴.
【点睛】本题考查了平行线的判定与性质,熟练掌握平行线的判定定理与性质定理是解题的关键.
26.见解析
【分析】根据平行的判定定理证明即可.
【详解】∵∠B+∠BAD=180°(已知),
∠1+∠BAD=180°(平角定义),
∴∠1=∠B(同角的补角相等).
∵∠1=∠2(已知),
∴∠2=∠B(等量代换).
∴ABCD(同位角相等,两条直线平行).
【点睛】本题考查平行线的判定定理,解题的关键是掌握平行线的判定定理:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
27.(1)①40;②∠1+∠2=60°,证明见解析;
(2)α+β=105°或α-β=15°
【分析】(1)①先标出∠3和∠4,然后再根据平行的性质可得∠1=∠3,∠2=∠4,然后再利用角的和差解答即可;
②如图:过点C作一条直线平行于格线,标出∠3和∠4 ,再根据平行的性质可得∠1=∠3,∠2=∠4,然后再利用角和差解答即可;
(2)分两种情况:当射线OC在∠AOB的内部,当射线OC在∠AOB的外部,然后利用平行线的性质和三角形的外角的性质进行计算,即可解答.
(1)
解:①如图1:标出∠3和∠4
由格线平行,利用平行的性质可得:∠1=∠3,∠2=∠4
∵∠3+∠4=∠AOB=60°,∠1=20°
∴∠1+∠2=60°
∴∠2=60°-20°=40°
故答案为:40;
②∠1+∠2=60°,证明如下:
证明:如图:过点C作一条直线平行于格线,标出∠3和∠4
由格线平行可得∠1=∠3,∠2=∠4
∵∠3+∠4=∠AOB=60°
∴∠1+∠2=60°.
(2)
解:设OA与图中一条格线形成的锐角为,OC与另一条格线形成的锐角为
当射线OC在∠AOB的内部,如图:
在图中随意选择两条格线标出、且过O点作平行于格线的辅助线,并标出∠1和∠2
由格线平行可得∠2=,∠1+∠2=
∵∠AOB=60°,∠COB=45°
∴∠AOC=15°即∠1=15°,∠1+=
∴=15°+
即
当射线OC在∠AOB的外部,如图:
∵∠COB=45°,∠AOB=60°
∴∠AOC=∠AOB+∠COB=105°
由(1)中②知,∠AOC=α+β
∴α+β=105°
综上所述:α+β=105°或α-β=15°.
【点睛】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.难点是作辅助线,第(2)要分类讨论,不要出现遗漏情况.
28.;理由见解析
【分析】先根据补角的定义求出的度数,然后求出∠CFE和∠2的度数,最后根据平行线的判定进行解答即可.
【详解】解:;理由如下:
∵是它的补角的3倍,
∴设,则的补角为,
∴,
解得:,
∴,
∴,
∵,
∴,
∴,
∴.
【点睛】本题主要考查了补角的有关计算,平行线的判定,根据题意求出,是解题的关键.
29.;同位角相等,两直线平行;;两直线平行,同位角相等;;内错角相等,两直线平行
【分析】先证明,可得,再证明,从而可得结论.
【详解】证明:∵,,
∴.
∴(同位角相等,两直线平行).
∴(两直线平行,同位角相等).
又∵,
∴.
∴(内错角相等,两直线平行).
【点睛】本题考查的是平行线的性质与判定,掌握“平行线的性质与平行线的判定方法以及简单的逻辑思维推理”是解本题的关键.
30.(1)证明见解析
(2)
【分析】(1)先根据垂直的定义可得,再根据平行线的判定可得,然后根据平行线的性质可得,从而可得,最后根据平行线的判定即可得证;
(2)连接,设,则,再根据建立方程,解方程可得,然后根据平行线的性质即可得.
(1)
证明:,
,
,
,
,
,
,
,
.
(2)
解:如图,连接,
设,
,
,
,
由(1)已得:,
,
,
解得,
即,
由(1)已证:,
.
【点睛】本题考查了平行线的判定与性质、垂直等知识点,熟练掌握平行线的判定与性质是解题关键.
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
