第五章 二元一次方程组 期末试题选编 (含解析)2021-2022学年北京市各地京改版数学七年级下册
文档属性
| 名称 | 第五章 二元一次方程组 期末试题选编 (含解析)2021-2022学年北京市各地京改版数学七年级下册 |  | |
| 格式 | zip | ||
| 文件大小 | 394.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 13:19:56 | ||
图片预览




文档简介
第五章 二元一次方程组
一、单选题
1.(2022春·北京怀柔·七年级校考期末)若方程ax+3y=2+4x是关于的二元一次方程,则a满足( )
A.a≠1 B.a≠2 C.a≠3 D.a≠4
2.(2022春·北京朝阳·七年级统考期末)若是二元一次方程的一个解,则m的值为( )
A. B. C.1 D.
3.(2022春·北京顺义·七年级统考期末)下列方程组中,解是的是( )
A. B. C. D.
4.(2022春·北京通州·七年级统考期末)已知二元一次方程的解,又是下列哪个方程的解( )
A. B. C. D.
5.(2022春·北京西城·七年级统考期末)解方程组的思路可用如图的框图表示,圈中应填写的对方程①②所做的变形为( )
A.①×2+②×3 B.①×2-②×3 C.①×3-②×2 D.①×3+②×2
6.(2022春·北京丰台·七年级统考期末)被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.书中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”原文大意为:“现在有5只雀、6只燕,分别集中放在天平上称重,聚在一起的雀重燕轻.将一只雀一只燕交换位置而放,重量相等,5只雀和6只燕共重1斤,问雀和燕各重多少?”设雀每只斤,燕每只斤,则可列出方程组为( )
A. B.
C. D.
二、填空题
7.(2022春·北京西城·七年级统考期末)若是方程的解,则a的值为______.
8.(2022春·北京丰台·七年级统考期末)已知是关于,的二元一次方程的解,则的值为______.
9.(2022春·北京平谷·七年级统考期末)观察下列表格,写出方程组的解是____________.
… …
… 2 …
… …
… 2 …
10.(2022春·北京石景山·七年级统考期末)已知是方程的一个解,则m的值是______.
11.(2022春·北京门头沟·七年级统考期末)把方程写成用含y的代数式表示x的形式,_____.
12.(2022春·北京房山·七年级统考期末)若有理数a,b满足,则a+b的值为______.
13.(2022秋·北京朝阳·七年级统考期末)下表是某校七年级各班某月课外兴趣小组活动时间的统计表,其中各班同一兴趣小组每次活动时间相同.
体育小组 活动次数 科技小组 活动次数 文艺小组 活动次数 课外兴趣小组 活动总时间(单位:h)
1 4 6 5 11.5
2 4 6 4 11
3 4 7 4 12
4 6 13
(说明:活动次数为正整数)
科技小组每次活动时间为____________h,该年级4班这个月体育小组活动次数最多是____________次.
14.(2022春·北京密云·七年级统考期末)《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现有30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,则可列二元一次方程组为_____.
15.(2022秋·北京平谷·七年级统考期末)《孙子算经》记载:今有3人共车,二车空;二人共车,九人步,问人与车各几何?译文:今有若干人乘车,若每三人共乘一辆车,最终剩余2辆车;若每2人共乘一辆车,最终剩余9人无车可乘.问共有多少人?多少辆车?若设有x辆车,有y人,则可列方程组为_____.
16.(2022春·北京昌平·七年级统考期末)某中学为积极开展校园足球运动,计划购买和两种品牌的足球,已知一个品牌足球价格为120元,一个品牌足球价格为150元.学校准备用3000元购买这两种足球(两种足球都买),并且3000元全部用完,请写出一种购买方案:买_______个品牌足球,买________个品牌足球.
17.(2022春·北京东城·七年级统考期末)2018年全国滑冰场地与滑雪场地共有1133个.到了2021年,全国滑冰场地与滑雪场地共有2261个,其中滑冰场地比2018年滑冰场地的2倍多232个,滑雪场地比2018年滑雪场地增加了287个.求2018年全国滑冰场地和滑雪场地各有多少个.设2018年全国滑冰场地和滑雪场地分别有个,个,依据题意,可列二元一次方程组为______.
三、解答题
18.(2022春·北京平谷·七年级统考期末)解方程组:
19.(2022春·北京丰台·七年级统考期末)解方程组:.
20.(2022春·北京海淀·七年级统考期末)解方程组:
21.(2022春·北京密云·七年级统考期末)已知关于x,y的二元一次方程组的解为,求的值.
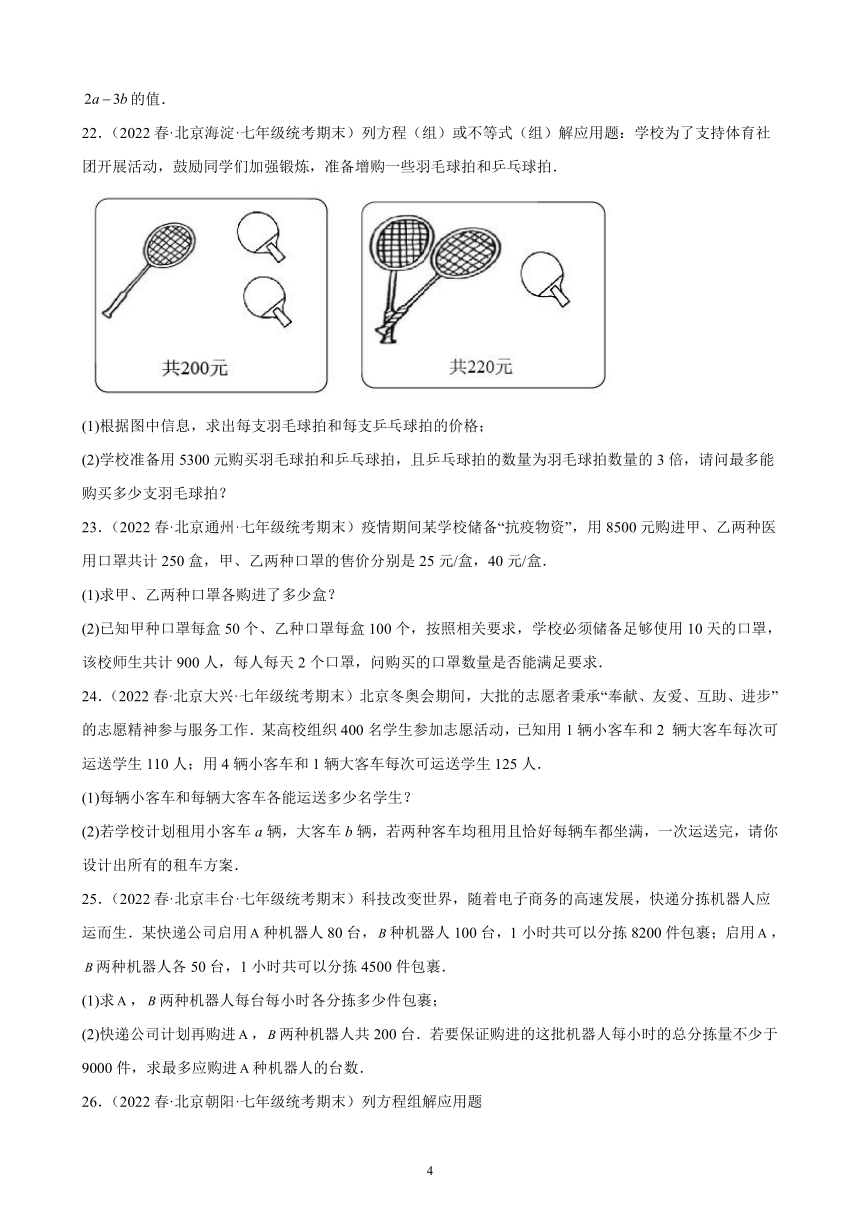
22.(2022春·北京海淀·七年级统考期末)列方程(组)或不等式(组)解应用题:学校为了支持体育社团开展活动,鼓励同学们加强锻炼,准备增购一些羽毛球拍和乒乓球拍.
(1)根据图中信息,求出每支羽毛球拍和每支乒乓球拍的价格;
(2)学校准备用5300元购买羽毛球拍和乒乓球拍,且乒乓球拍的数量为羽毛球拍数量的3倍,请问最多能购买多少支羽毛球拍?
23.(2022春·北京通州·七年级统考期末)疫情期间某学校储备“抗疫物资”,用8500元购进甲、乙两种医用口罩共计250盒,甲、乙两种口罩的售价分别是25元/盒,40元/盒.
(1)求甲、乙两种口罩各购进了多少盒?
(2)已知甲种口罩每盒50个、乙种口罩每盒100个,按照相关要求,学校必须储备足够使用10天的口罩,该校师生共计900人,每人每天2个口罩,问购买的口罩数量是否能满足要求.
24.(2022春·北京大兴·七年级统考期末)北京冬奥会期间,大批的志愿者秉承“奉献、友爱、互助、进步”的志愿精神参与服务工作.某高校组织400名学生参加志愿活动,已知用1辆小客车和2 辆大客车每次可运送学生110人;用4辆小客车和1辆大客车每次可运送学生125人.
(1)每辆小客车和每辆大客车各能运送多少名学生?
(2)若学校计划租用小客车a辆,大客车b辆,若两种客车均租用且恰好每辆车都坐满,一次运送完,请你设计出所有的租车方案.
25.(2022春·北京丰台·七年级统考期末)科技改变世界,随着电子商务的高速发展,快递分拣机器人应运而生.某快递公司启用种机器人80台,种机器人100台,1小时共可以分拣8200件包裹;启用,两种机器人各50台,1小时共可以分拣4500件包裹.
(1)求,两种机器人每台每小时各分拣多少件包裹;
(2)快递公司计划再购进,两种机器人共200台.若要保证购进的这批机器人每小时的总分拣量不少于9000件,求最多应购进种机器人的台数.
26.(2022春·北京朝阳·七年级统考期末)列方程组解应用题
根据一次市场调查,了解到某种消毒液的大瓶装(1500g)和小瓶装(500g)两种产品的销售数量(按瓶计算)比为4:3,某工厂每天生产这种消毒液30t(1t=1 000 000 g),这些消毒液应该分装大、小瓶两种产品各多少瓶?
27.(2022春·北京延庆·七年级统考期末)某校七年级(1)班、(2)班的同学积极参加全民健身活动,为此两班到同一商店购买体育用品.已知七年级(1)班买了3个篮球和4副羽毛球拍共用了270元;七年级(2)班买了同样的5个篮球和6副羽毛球拍共用了430元;问每个篮球和每副羽毛球拍各多少元?
28.(2022春·北京平谷·七年级统考期末)列方程(组)解应用题:
平谷区某食用菌种植合作社将废弃树枝秸秆粉碎后制作成蘑菇菌棒.废菌棒经过高温灭虫后还田,生产性废料循环利用还可以改善土壤PH值(土壤酸碱度)和板结的情况,抑制杂草生长,改善蔬果口感.合作社积极鼓励村民用废弃树枝秸秆换取菌棒,培训推广科学种植菌菇技术,扩大种植规模,让更多的村民能够拥有一技之长,形成一条绿色循环生态产业链,实现生态效益与经济效益双赢.现合作社准备购进一批加工菌棒的设备,现有A,B两种型号的设备,经调查购买一台A型号的设备比购买一台B型号的设备多2万元;购买2台A型号的设备比购买3台B型号的设备少1万元.求A,B两种型号的设备每台各多少万元?
29.(2022春·北京西城·七年级统考期末)随着我国物流行业市场的成熟发展和技术成熟度的显著提升,物流无人机的市场价格下降很快,物流无人机得到了广泛的应用.已知1架甲型物流无人机与7架乙型物流无人机总价为435万元,2架甲型物流无人机与9架乙型物流无人机总价为845万元.甲型和乙型物流无人机每架各多少万元?
30.(2022春·北京顺义·七年级统考期末)列方程组解应用题:
已知1支百合和2支康乃馨共14元,2支百合和3支康乃馨共24元.求一支百合和一支康乃馨各多少元
参考答案:
1.D
【分析】移项整理给出的方程,根据二元一次方程的定义确定a的范围.
【详解】解:移项,得ax 4x+3y 2=0,
整理,得(a 4)x+3y 2=0.
∵方程是关于x、y的二元一次方程,
∴a 4≠0.
∴a≠4.
故选:D.
【点睛】本题考查了二元一次方程的定义,理解二元一次方程的定义是解决本题的关键.二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程.
2.C
【分析】把与的值代入方程计算即可求出的值.
【详解】解:把代入方程得:,
解得:,
故选:C.
【点睛】此题考查了二元一次方程的解,方程组的解即为能使方程左右两边相等的未知数的值.
3.A
【分析】把代入各方程组两个方程检验,即可作出判断.
【详解】解:A、,
把代入①得:左边,右边,成立;
代入②得:左边,右边,成立,符合题意;
B、,
把代入①得:,右边,不符合题意;
C、,
把代入①得:左边,右边,不符合题意;
D、,
把代入①得:左边,右边;
把代入②得:左边,右边,不符合题意.
故选:A.
【点睛】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.
4.B
【分析】把x、y的值代入方程,看看方程两边是否相等即可.
【详解】解:A、把代入方程y=x+1,左边≠右边,
所以不是方程y=x+1的解,故本选项不符合题意;
B、把代入方程y=x-1,左边=右边,
所以是方程y=x-1的解,故本选项符合题意;
C、把代入方程y=-x+1,左边≠右边,
所以不是方程y=-x+1的解,故本选项不符合题意;
D、把代入方程y=-x-1,左边=右边,
所以不是方程y=-x-1的解,故本选项不符合题意.
故选B.
【点睛】本题考查了二元一次方程的解,能理解二元一次方程的解的意义是解此题的关键.
5.C
【分析】消去未知数x,变形思路是①×3-②×2,再得出选项即可.
【详解】解:,
①×3,得6x+9y=24③,
②×2,得6x-4y=-2④,
③-④,得(6x+9y)-(6x-4y)=24-(-2),
即变形的思路是①×3-②×2,
故选:C.
【点睛】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.
6.A
【分析】根据将一只雀一只燕交换位置而放,重量相等,可得4x+y=5y+x,根据5只雀、6只燕重量共一斤,可得5x+6y=1,从而可以得到相应的方程组,本题得以解决.
【详解】解:设每只雀有x斤,每只燕有y斤,
由题意得,.
故选:A.
【点睛】本题考查了有实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
7.3
【分析】把代入方程,得到关于a的一元一次方程,解方程即可求出a的值.
【详解】解:把代入方程得:2+2a=8,
∴a=3,
故答案为:3.
【点睛】本题考查了二元一次方程的解,把方程的解代入方程,得到关于a的一元一次方程是解题的关键.
8.
【分析】把代入方程,再解关于a的方程,从而可得答案.
【详解】解:∵是关于,的二元一次方程的解,
∴
解得:
故答案为:
【点睛】本题考查的是二元一次方程组的解的含义,掌握“方程的解使方程的左右两边的值相等”是解本题的关键.
9.
【分析】观察表格找出两个方程的公共解,即可得到方程组的解.
【详解】解:观察表格可以发现,
x=8和是两方程的公共解,
∴原方程组的解为;
故答案为:.
【点睛】本题考查了二元一次方程组的解,解题的关键是理解方程组的解.
10.4
【分析】已知方程组的解,将代入原方程即可求出m.
【详解】将代入得:-2+3m=10,解得:m=4
故答案为:4
【点睛】本题主要考查了二元一次方程得解,已知方程的解则可以把解代入原方程得到一个新的参数方程,正确的理解和掌握方程的解的概念是解题的关键.
11.
【分析】把y看作已知数表示出x即可.
【详解】方程,
移项得:
系数化1得:
故答案为:.
【点睛】此题考查了解二元一次方程,解题的关键是将一个未知数看作已知数求出另一个未知数.
12.-2
【分析】根据,可知,,故可求出a+b.
【详解】解:∵,
∴,令①+②可得:,
∴,
故答案为: 2
【点睛】本题对于绝对值和平方的非负性及求二元一次方程组的解的考查,理解两个非负数的和等于零时每一个非负数必为零的特点是解题的关键.
13. 1 8
【分析】设体育小组每次活动时间为a小时,科技小组每次活动时间为b小时,文艺小组每次活动时间为c小时,根据1、2、3班每班活动总时间列方程组求解即可;设该年级4班这个月体育小组活动次数为m,文艺小组活动次数为n,根据4班总活动时间列方程求得方程的正整数解即可;
【详解】解:设体育小组每次活动时间为a小时,科技小组每次活动时间为b小时,文艺小组每次活动时间为c小时,则
①-②得:c=0.5,
c=0.5代入①得:4a+6b=9,
③-②得: b=1,
4a+6b=9,a=0.75,
∴体育小组每次活动时间为0.75小时,科技小组每次活动时间为1小时,文艺小组每次活动时间为0.5小时;
设该年级4班这个月体育小组活动次数为m,文艺小组活动次数为n,则
0.75m+6+0.5n=13,
0.75m+0.5n=7,
1.5m+n=14,
∵m,n为正整数,
∴m=2,n=11或m=4,n=8或m=6,n=5或m=8,n=2;
m最大值为8次,
故答案为:1,8;
【点睛】本题考查了三元一次方程的实际应用,二元一次方程的正整数解,利用加减消元法解方程是解题关键.
14.
【分析】设买美酒x斗,买普通酒y斗,根据“美酒一斗的价格是50钱、买两种酒2斗共付30钱”列出方程组.
【详解】设买美酒x斗,买普通酒y斗,
依题意得:,
故答案是:.
【点睛】考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
15.
【分析】根据两种乘车方式,找出等量关系,由此建立方程组即可.
【详解】由题意,可列方程组为:,
故答案为:.
【点睛】本题考查了列二元一次方程组,依据题意,正确找出等量关系是解题关键.
16. 10 12
【分析】设买个品牌足球,买个品牌足球,根据题意列出二元一次方程,根据整数解确定的值即可求解.
【详解】解:设买个品牌足球,买个品牌足球,根据题意得,
,
整理得:,
,是正整数,
是5的倍数,
.
故答案为:(答案不唯一).
【点睛】本题考查了二元一次方程的应用,整除,根据题意列出方程是解题的关键.
17.
【分析】根据2018年全国滑冰场地与滑雪场地共有1133个;到了2021年,全国滑冰场地与滑雪场地共有2261个,列方程组即可.
【详解】解:由题意得:.
故答案为:.
【点睛】本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
18.
【分析】先把方程①化为,再代入方程②求解y,再求解x,即可得到答案.
【详解】解:
由①得③
把③代入②,得.
解得 ,
把代入③得: ,
所以这个方程组的解是
【点睛】本题考查的是二元一次方程组的解法,掌握“代入消元法解二元一次方程组”是解本题的关键.
19.
【分析】利用加减消元法解方程组即可.
【详解】解:方程组:,
①×2得,
②+③得,
解得,
把代入①得.
所以是原方程组的解.
【点睛】此题主要考查了二元一次方程组的解法,根据题目特点灵活选用加减消元法或代入消元法求解是关键.
20.
【分析】利用加减消元法消去y,再解一元一次方程即可.
【详解】解:
将得:,
∴,
将代入②得:,
∴,
∴该方程组的解为.
【点睛】本题考查了二元一次方程组的解法,解题关键是正确运用加减消元法消去y,得到关于x的一元一次方程.
21.
【分析】先将方程组的解代入原方程组得到关于a,b的方程组,求出a,b的值代入求值即可.
【详解】解:由题意得:
解关于、的方程组得:
∴.
【点睛】本题考查二元一次方程组的解及求代数式的值,熟悉二元一次方程组的解法是解题关键.
22.(1)每支羽毛球拍80元,每支乒乓球拍60元
(2)最多能购买20支羽毛球拍
【分析】(1)设每支羽毛球拍x元,每支乒乓球拍y元,根据图中信息列出方程组,解方程即可;
(2)设羽毛球拍数量m个,则乒乓球拍的数量3m个,根据题意列出不等式解得即可.
(1)
设每支羽毛球拍x元,每支乒乓球拍y元,
,
解得,
答:每支羽毛球拍80元,每支乒乓球拍60元;
(2)
设羽毛球拍数量m个,则乒乓球拍的数量3m个,
由题意得:,
解得,
∴整式m的最大值为20,
∴最多能购买20支羽毛球拍.
【点睛】本题考查了二元一次方程组和一元一次不等式的应用,解题的关键是读懂题意列出方程和不等式.
23.(1)甲种口罩购进了100盒,乙种口罩购进了150盒;
(2)购买的口罩数量能满足相关要求.
【分析】(1)设甲种口罩购进了x盒,乙种口罩购进了y盒,根据口罩总盒数和总花费列方程组计算求值即可;
(2)根据(1)解答可得口罩总数量,再求得10天内所需口罩总数量进行比较即可解答;
(1)
解:设甲种口罩购进了x盒,乙种口罩购进了y盒,
据题意得:,
①×40-②得:15x=1500,
解得:x=100,
x=100代入x+y=250得:y=150,
方程组的解为:,
答:甲种口罩购进了100盒,乙种口罩购进了150盒.
(2)
解:由题意得:
口罩总数量=(个),
10天内所需口罩总数量=(个),
∵20000>18000,
∴购买的口罩数量能满足相关要求;
【点睛】本题考查了二元一次方程组的实际应用,找准题中等量关系列方程是解题关键.
24.(1)每辆小客车能运送20名学生,每辆大客车能运送45名学生
(2)租车方案为:小客车11辆,大客车4辆或小客车2辆,大客车8辆
【分析】(1)设每辆小客车能坐x名学生,每辆大客车能坐y名学生,根据“用1辆小客车和2辆大客车每次可运送学生110人;用4辆小客车和1辆大客车每次可运送学生125人”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)①根据“一次运送400名学生,且恰好每辆车都坐满”,即可得出关于a,b的二元一次方程,结合a,b均为正整数,即可得出各租车方案;
(1)
设每辆小客车能运送x名学生,每辆大客车能运送y名学生.
根据题意,得:.
解得:.
答:每辆小客车能运送20名学生,每辆大客车能运送45名学生.
(2)
根据题意,得.
∴.
∵a,b为正整数,两种客车均租用且恰好每辆车都坐满
∴或.
答:租车方案为:小客车11辆,大客车4辆或小客车2辆,大客车8辆.
【点睛】本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程.
25.(1)A种机器人每台每小时分拣40件包裹,B种机器人每台每小时分拣50件包裹
(2)最多应购进A种机器人100台
【分析】(1)设A种机器人每台每小时分拣x件包裹,B种机器人每台每小时分拣y件包裹,列方程组,解出即可;
(2)设购进A种机器人m台,则购进B种机器人(200-m)台,根据题意列不等式40m+50(200-m)≥9000,求最大整数解即可.
(1)
设A种机器人每台每小时分拣x件包裹,B种机器人每台每小时分拣y件包裹,
根据题意,得
解得,
答:A种机器人每台每小时分拣40件包裹,B种机器人每台每小时分拣50件包裹.
(2)
设购进A种机器人m台,则购进B种机器人(200-m)台.
根据题意,得40m+50(200-m)≥9000,
解得m≤100.
答:最多应购进A种机器人100台.
【点睛】本题考查了一元一次不等式的应用、二元一次方程组的应用,正确理解题意是解题关键.
26.大瓶产品16000瓶,小瓶产品12000瓶
【分析】设这些消毒液应分装大瓶产品瓶,小瓶产品瓶,根据题意列二元一次方程组,求解即可.
【详解】解:设这些消毒液应分装大瓶产品瓶,小瓶产品瓶,
根据题意,得,
解得,
答:这些消毒液应分装大瓶产品16000瓶,小瓶产品12000瓶.
【点睛】本题考查了二元一次方程组的应用,根据题意建立合适的等量关系是解题的关键.
27.每个篮球50元,每副羽毛球拍30元
【分析】设每个篮球元,每副羽毛球拍元,由题意:七年级(1)班购买了3个篮球和4副羽毛球拍共用了270元,七年级(2)班购买了同样的5个篮球和6副羽毛球拍共用了430元,列出二元一次方程组,解方程组即可.
【详解】解:设每个篮球元,每副羽毛球拍元,
根据题意列方程组,得,
解这个方程组,得.
答:每个篮球50元,每副羽毛球拍30元.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
28.A型号设备7万元/台,B型号设备5万元/台
【分析】由题意,设A型号设备x万元/台,B型号设备y万元/台,然后列出方程组,解方程组即可得到答案.
【详解】解:设A型号设备x万元/台,B型号设备y万元/台.
根据题意列方程组,得:
解方程得:.
答:A型号设备7万元/台,B型号设备5万元/台.
【点睛】本题考查了二元一次方程组的应用,解题的关键是熟练掌握题意,正确的理解题意,从而进行解题.
29.甲型物流无人机每架400万元,乙型物流无人机每架5万元
【分析】设甲型物流无人机每架x万元,乙型物流无人机每架y万元,根据“1架甲型物流无人机与7架乙型物流无人机总价为435万元,2架甲型物流无人机与9架乙型物流无人机总价为845万元”即可列出二元一次方程组.
【详解】解:设甲型物流无人机每架x万元,乙型物流无人机每架y万元,
根据题意得,,
解得:,
答:甲型物流无人机每架400万元,乙型物流无人机每架5万元.
【点睛】本题主要考查了二元一次方程组的应用,根据总价找出等量关系是解决问题的关键.
30.一支百合6元,一支康乃馨4元
【分析】设一支百合x 元,一支康乃馨y元,由题意:1支百合和2支康乃馨共14元,2支百合和3支康乃馨共24元.列出二元一次方程组,解方程组即可.
【详解】解:设一支百合x 元,一支康乃馨y元,
依题意得:,
解得:,
答:一支百合6元,一支康乃馨4元.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
一、单选题
1.(2022春·北京怀柔·七年级校考期末)若方程ax+3y=2+4x是关于的二元一次方程,则a满足( )
A.a≠1 B.a≠2 C.a≠3 D.a≠4
2.(2022春·北京朝阳·七年级统考期末)若是二元一次方程的一个解,则m的值为( )
A. B. C.1 D.
3.(2022春·北京顺义·七年级统考期末)下列方程组中,解是的是( )
A. B. C. D.
4.(2022春·北京通州·七年级统考期末)已知二元一次方程的解,又是下列哪个方程的解( )
A. B. C. D.
5.(2022春·北京西城·七年级统考期末)解方程组的思路可用如图的框图表示,圈中应填写的对方程①②所做的变形为( )
A.①×2+②×3 B.①×2-②×3 C.①×3-②×2 D.①×3+②×2
6.(2022春·北京丰台·七年级统考期末)被历代数学家尊为“算经之首”的《九章算术》是中国古代算法的扛鼎之作.书中记载:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”原文大意为:“现在有5只雀、6只燕,分别集中放在天平上称重,聚在一起的雀重燕轻.将一只雀一只燕交换位置而放,重量相等,5只雀和6只燕共重1斤,问雀和燕各重多少?”设雀每只斤,燕每只斤,则可列出方程组为( )
A. B.
C. D.
二、填空题
7.(2022春·北京西城·七年级统考期末)若是方程的解,则a的值为______.
8.(2022春·北京丰台·七年级统考期末)已知是关于,的二元一次方程的解,则的值为______.
9.(2022春·北京平谷·七年级统考期末)观察下列表格,写出方程组的解是____________.
… …
… 2 …
… …
… 2 …
10.(2022春·北京石景山·七年级统考期末)已知是方程的一个解,则m的值是______.
11.(2022春·北京门头沟·七年级统考期末)把方程写成用含y的代数式表示x的形式,_____.
12.(2022春·北京房山·七年级统考期末)若有理数a,b满足,则a+b的值为______.
13.(2022秋·北京朝阳·七年级统考期末)下表是某校七年级各班某月课外兴趣小组活动时间的统计表,其中各班同一兴趣小组每次活动时间相同.
体育小组 活动次数 科技小组 活动次数 文艺小组 活动次数 课外兴趣小组 活动总时间(单位:h)
1 4 6 5 11.5
2 4 6 4 11
3 4 7 4 12
4 6 13
(说明:活动次数为正整数)
科技小组每次活动时间为____________h,该年级4班这个月体育小组活动次数最多是____________次.
14.(2022春·北京密云·七年级统考期末)《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现有30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,则可列二元一次方程组为_____.
15.(2022秋·北京平谷·七年级统考期末)《孙子算经》记载:今有3人共车,二车空;二人共车,九人步,问人与车各几何?译文:今有若干人乘车,若每三人共乘一辆车,最终剩余2辆车;若每2人共乘一辆车,最终剩余9人无车可乘.问共有多少人?多少辆车?若设有x辆车,有y人,则可列方程组为_____.
16.(2022春·北京昌平·七年级统考期末)某中学为积极开展校园足球运动,计划购买和两种品牌的足球,已知一个品牌足球价格为120元,一个品牌足球价格为150元.学校准备用3000元购买这两种足球(两种足球都买),并且3000元全部用完,请写出一种购买方案:买_______个品牌足球,买________个品牌足球.
17.(2022春·北京东城·七年级统考期末)2018年全国滑冰场地与滑雪场地共有1133个.到了2021年,全国滑冰场地与滑雪场地共有2261个,其中滑冰场地比2018年滑冰场地的2倍多232个,滑雪场地比2018年滑雪场地增加了287个.求2018年全国滑冰场地和滑雪场地各有多少个.设2018年全国滑冰场地和滑雪场地分别有个,个,依据题意,可列二元一次方程组为______.
三、解答题
18.(2022春·北京平谷·七年级统考期末)解方程组:
19.(2022春·北京丰台·七年级统考期末)解方程组:.
20.(2022春·北京海淀·七年级统考期末)解方程组:
21.(2022春·北京密云·七年级统考期末)已知关于x,y的二元一次方程组的解为,求的值.
22.(2022春·北京海淀·七年级统考期末)列方程(组)或不等式(组)解应用题:学校为了支持体育社团开展活动,鼓励同学们加强锻炼,准备增购一些羽毛球拍和乒乓球拍.
(1)根据图中信息,求出每支羽毛球拍和每支乒乓球拍的价格;
(2)学校准备用5300元购买羽毛球拍和乒乓球拍,且乒乓球拍的数量为羽毛球拍数量的3倍,请问最多能购买多少支羽毛球拍?
23.(2022春·北京通州·七年级统考期末)疫情期间某学校储备“抗疫物资”,用8500元购进甲、乙两种医用口罩共计250盒,甲、乙两种口罩的售价分别是25元/盒,40元/盒.
(1)求甲、乙两种口罩各购进了多少盒?
(2)已知甲种口罩每盒50个、乙种口罩每盒100个,按照相关要求,学校必须储备足够使用10天的口罩,该校师生共计900人,每人每天2个口罩,问购买的口罩数量是否能满足要求.
24.(2022春·北京大兴·七年级统考期末)北京冬奥会期间,大批的志愿者秉承“奉献、友爱、互助、进步”的志愿精神参与服务工作.某高校组织400名学生参加志愿活动,已知用1辆小客车和2 辆大客车每次可运送学生110人;用4辆小客车和1辆大客车每次可运送学生125人.
(1)每辆小客车和每辆大客车各能运送多少名学生?
(2)若学校计划租用小客车a辆,大客车b辆,若两种客车均租用且恰好每辆车都坐满,一次运送完,请你设计出所有的租车方案.
25.(2022春·北京丰台·七年级统考期末)科技改变世界,随着电子商务的高速发展,快递分拣机器人应运而生.某快递公司启用种机器人80台,种机器人100台,1小时共可以分拣8200件包裹;启用,两种机器人各50台,1小时共可以分拣4500件包裹.
(1)求,两种机器人每台每小时各分拣多少件包裹;
(2)快递公司计划再购进,两种机器人共200台.若要保证购进的这批机器人每小时的总分拣量不少于9000件,求最多应购进种机器人的台数.
26.(2022春·北京朝阳·七年级统考期末)列方程组解应用题
根据一次市场调查,了解到某种消毒液的大瓶装(1500g)和小瓶装(500g)两种产品的销售数量(按瓶计算)比为4:3,某工厂每天生产这种消毒液30t(1t=1 000 000 g),这些消毒液应该分装大、小瓶两种产品各多少瓶?
27.(2022春·北京延庆·七年级统考期末)某校七年级(1)班、(2)班的同学积极参加全民健身活动,为此两班到同一商店购买体育用品.已知七年级(1)班买了3个篮球和4副羽毛球拍共用了270元;七年级(2)班买了同样的5个篮球和6副羽毛球拍共用了430元;问每个篮球和每副羽毛球拍各多少元?
28.(2022春·北京平谷·七年级统考期末)列方程(组)解应用题:
平谷区某食用菌种植合作社将废弃树枝秸秆粉碎后制作成蘑菇菌棒.废菌棒经过高温灭虫后还田,生产性废料循环利用还可以改善土壤PH值(土壤酸碱度)和板结的情况,抑制杂草生长,改善蔬果口感.合作社积极鼓励村民用废弃树枝秸秆换取菌棒,培训推广科学种植菌菇技术,扩大种植规模,让更多的村民能够拥有一技之长,形成一条绿色循环生态产业链,实现生态效益与经济效益双赢.现合作社准备购进一批加工菌棒的设备,现有A,B两种型号的设备,经调查购买一台A型号的设备比购买一台B型号的设备多2万元;购买2台A型号的设备比购买3台B型号的设备少1万元.求A,B两种型号的设备每台各多少万元?
29.(2022春·北京西城·七年级统考期末)随着我国物流行业市场的成熟发展和技术成熟度的显著提升,物流无人机的市场价格下降很快,物流无人机得到了广泛的应用.已知1架甲型物流无人机与7架乙型物流无人机总价为435万元,2架甲型物流无人机与9架乙型物流无人机总价为845万元.甲型和乙型物流无人机每架各多少万元?
30.(2022春·北京顺义·七年级统考期末)列方程组解应用题:
已知1支百合和2支康乃馨共14元,2支百合和3支康乃馨共24元.求一支百合和一支康乃馨各多少元
参考答案:
1.D
【分析】移项整理给出的方程,根据二元一次方程的定义确定a的范围.
【详解】解:移项,得ax 4x+3y 2=0,
整理,得(a 4)x+3y 2=0.
∵方程是关于x、y的二元一次方程,
∴a 4≠0.
∴a≠4.
故选:D.
【点睛】本题考查了二元一次方程的定义,理解二元一次方程的定义是解决本题的关键.二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程.
2.C
【分析】把与的值代入方程计算即可求出的值.
【详解】解:把代入方程得:,
解得:,
故选:C.
【点睛】此题考查了二元一次方程的解,方程组的解即为能使方程左右两边相等的未知数的值.
3.A
【分析】把代入各方程组两个方程检验,即可作出判断.
【详解】解:A、,
把代入①得:左边,右边,成立;
代入②得:左边,右边,成立,符合题意;
B、,
把代入①得:,右边,不符合题意;
C、,
把代入①得:左边,右边,不符合题意;
D、,
把代入①得:左边,右边;
把代入②得:左边,右边,不符合题意.
故选:A.
【点睛】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.
4.B
【分析】把x、y的值代入方程,看看方程两边是否相等即可.
【详解】解:A、把代入方程y=x+1,左边≠右边,
所以不是方程y=x+1的解,故本选项不符合题意;
B、把代入方程y=x-1,左边=右边,
所以是方程y=x-1的解,故本选项符合题意;
C、把代入方程y=-x+1,左边≠右边,
所以不是方程y=-x+1的解,故本选项不符合题意;
D、把代入方程y=-x-1,左边=右边,
所以不是方程y=-x-1的解,故本选项不符合题意.
故选B.
【点睛】本题考查了二元一次方程的解,能理解二元一次方程的解的意义是解此题的关键.
5.C
【分析】消去未知数x,变形思路是①×3-②×2,再得出选项即可.
【详解】解:,
①×3,得6x+9y=24③,
②×2,得6x-4y=-2④,
③-④,得(6x+9y)-(6x-4y)=24-(-2),
即变形的思路是①×3-②×2,
故选:C.
【点睛】本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键.
6.A
【分析】根据将一只雀一只燕交换位置而放,重量相等,可得4x+y=5y+x,根据5只雀、6只燕重量共一斤,可得5x+6y=1,从而可以得到相应的方程组,本题得以解决.
【详解】解:设每只雀有x斤,每只燕有y斤,
由题意得,.
故选:A.
【点睛】本题考查了有实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
7.3
【分析】把代入方程,得到关于a的一元一次方程,解方程即可求出a的值.
【详解】解:把代入方程得:2+2a=8,
∴a=3,
故答案为:3.
【点睛】本题考查了二元一次方程的解,把方程的解代入方程,得到关于a的一元一次方程是解题的关键.
8.
【分析】把代入方程,再解关于a的方程,从而可得答案.
【详解】解:∵是关于,的二元一次方程的解,
∴
解得:
故答案为:
【点睛】本题考查的是二元一次方程组的解的含义,掌握“方程的解使方程的左右两边的值相等”是解本题的关键.
9.
【分析】观察表格找出两个方程的公共解,即可得到方程组的解.
【详解】解:观察表格可以发现,
x=8和是两方程的公共解,
∴原方程组的解为;
故答案为:.
【点睛】本题考查了二元一次方程组的解,解题的关键是理解方程组的解.
10.4
【分析】已知方程组的解,将代入原方程即可求出m.
【详解】将代入得:-2+3m=10,解得:m=4
故答案为:4
【点睛】本题主要考查了二元一次方程得解,已知方程的解则可以把解代入原方程得到一个新的参数方程,正确的理解和掌握方程的解的概念是解题的关键.
11.
【分析】把y看作已知数表示出x即可.
【详解】方程,
移项得:
系数化1得:
故答案为:.
【点睛】此题考查了解二元一次方程,解题的关键是将一个未知数看作已知数求出另一个未知数.
12.-2
【分析】根据,可知,,故可求出a+b.
【详解】解:∵,
∴,令①+②可得:,
∴,
故答案为: 2
【点睛】本题对于绝对值和平方的非负性及求二元一次方程组的解的考查,理解两个非负数的和等于零时每一个非负数必为零的特点是解题的关键.
13. 1 8
【分析】设体育小组每次活动时间为a小时,科技小组每次活动时间为b小时,文艺小组每次活动时间为c小时,根据1、2、3班每班活动总时间列方程组求解即可;设该年级4班这个月体育小组活动次数为m,文艺小组活动次数为n,根据4班总活动时间列方程求得方程的正整数解即可;
【详解】解:设体育小组每次活动时间为a小时,科技小组每次活动时间为b小时,文艺小组每次活动时间为c小时,则
①-②得:c=0.5,
c=0.5代入①得:4a+6b=9,
③-②得: b=1,
4a+6b=9,a=0.75,
∴体育小组每次活动时间为0.75小时,科技小组每次活动时间为1小时,文艺小组每次活动时间为0.5小时;
设该年级4班这个月体育小组活动次数为m,文艺小组活动次数为n,则
0.75m+6+0.5n=13,
0.75m+0.5n=7,
1.5m+n=14,
∵m,n为正整数,
∴m=2,n=11或m=4,n=8或m=6,n=5或m=8,n=2;
m最大值为8次,
故答案为:1,8;
【点睛】本题考查了三元一次方程的实际应用,二元一次方程的正整数解,利用加减消元法解方程是解题关键.
14.
【分析】设买美酒x斗,买普通酒y斗,根据“美酒一斗的价格是50钱、买两种酒2斗共付30钱”列出方程组.
【详解】设买美酒x斗,买普通酒y斗,
依题意得:,
故答案是:.
【点睛】考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
15.
【分析】根据两种乘车方式,找出等量关系,由此建立方程组即可.
【详解】由题意,可列方程组为:,
故答案为:.
【点睛】本题考查了列二元一次方程组,依据题意,正确找出等量关系是解题关键.
16. 10 12
【分析】设买个品牌足球,买个品牌足球,根据题意列出二元一次方程,根据整数解确定的值即可求解.
【详解】解:设买个品牌足球,买个品牌足球,根据题意得,
,
整理得:,
,是正整数,
是5的倍数,
.
故答案为:(答案不唯一).
【点睛】本题考查了二元一次方程的应用,整除,根据题意列出方程是解题的关键.
17.
【分析】根据2018年全国滑冰场地与滑雪场地共有1133个;到了2021年,全国滑冰场地与滑雪场地共有2261个,列方程组即可.
【详解】解:由题意得:.
故答案为:.
【点睛】本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组.
18.
【分析】先把方程①化为,再代入方程②求解y,再求解x,即可得到答案.
【详解】解:
由①得③
把③代入②,得.
解得 ,
把代入③得: ,
所以这个方程组的解是
【点睛】本题考查的是二元一次方程组的解法,掌握“代入消元法解二元一次方程组”是解本题的关键.
19.
【分析】利用加减消元法解方程组即可.
【详解】解:方程组:,
①×2得,
②+③得,
解得,
把代入①得.
所以是原方程组的解.
【点睛】此题主要考查了二元一次方程组的解法,根据题目特点灵活选用加减消元法或代入消元法求解是关键.
20.
【分析】利用加减消元法消去y,再解一元一次方程即可.
【详解】解:
将得:,
∴,
将代入②得:,
∴,
∴该方程组的解为.
【点睛】本题考查了二元一次方程组的解法,解题关键是正确运用加减消元法消去y,得到关于x的一元一次方程.
21.
【分析】先将方程组的解代入原方程组得到关于a,b的方程组,求出a,b的值代入求值即可.
【详解】解:由题意得:
解关于、的方程组得:
∴.
【点睛】本题考查二元一次方程组的解及求代数式的值,熟悉二元一次方程组的解法是解题关键.
22.(1)每支羽毛球拍80元,每支乒乓球拍60元
(2)最多能购买20支羽毛球拍
【分析】(1)设每支羽毛球拍x元,每支乒乓球拍y元,根据图中信息列出方程组,解方程即可;
(2)设羽毛球拍数量m个,则乒乓球拍的数量3m个,根据题意列出不等式解得即可.
(1)
设每支羽毛球拍x元,每支乒乓球拍y元,
,
解得,
答:每支羽毛球拍80元,每支乒乓球拍60元;
(2)
设羽毛球拍数量m个,则乒乓球拍的数量3m个,
由题意得:,
解得,
∴整式m的最大值为20,
∴最多能购买20支羽毛球拍.
【点睛】本题考查了二元一次方程组和一元一次不等式的应用,解题的关键是读懂题意列出方程和不等式.
23.(1)甲种口罩购进了100盒,乙种口罩购进了150盒;
(2)购买的口罩数量能满足相关要求.
【分析】(1)设甲种口罩购进了x盒,乙种口罩购进了y盒,根据口罩总盒数和总花费列方程组计算求值即可;
(2)根据(1)解答可得口罩总数量,再求得10天内所需口罩总数量进行比较即可解答;
(1)
解:设甲种口罩购进了x盒,乙种口罩购进了y盒,
据题意得:,
①×40-②得:15x=1500,
解得:x=100,
x=100代入x+y=250得:y=150,
方程组的解为:,
答:甲种口罩购进了100盒,乙种口罩购进了150盒.
(2)
解:由题意得:
口罩总数量=(个),
10天内所需口罩总数量=(个),
∵20000>18000,
∴购买的口罩数量能满足相关要求;
【点睛】本题考查了二元一次方程组的实际应用,找准题中等量关系列方程是解题关键.
24.(1)每辆小客车能运送20名学生,每辆大客车能运送45名学生
(2)租车方案为:小客车11辆,大客车4辆或小客车2辆,大客车8辆
【分析】(1)设每辆小客车能坐x名学生,每辆大客车能坐y名学生,根据“用1辆小客车和2辆大客车每次可运送学生110人;用4辆小客车和1辆大客车每次可运送学生125人”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)①根据“一次运送400名学生,且恰好每辆车都坐满”,即可得出关于a,b的二元一次方程,结合a,b均为正整数,即可得出各租车方案;
(1)
设每辆小客车能运送x名学生,每辆大客车能运送y名学生.
根据题意,得:.
解得:.
答:每辆小客车能运送20名学生,每辆大客车能运送45名学生.
(2)
根据题意,得.
∴.
∵a,b为正整数,两种客车均租用且恰好每辆车都坐满
∴或.
答:租车方案为:小客车11辆,大客车4辆或小客车2辆,大客车8辆.
【点睛】本题考查了二元一次方程组的应用以及二元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出二元一次方程.
25.(1)A种机器人每台每小时分拣40件包裹,B种机器人每台每小时分拣50件包裹
(2)最多应购进A种机器人100台
【分析】(1)设A种机器人每台每小时分拣x件包裹,B种机器人每台每小时分拣y件包裹,列方程组,解出即可;
(2)设购进A种机器人m台,则购进B种机器人(200-m)台,根据题意列不等式40m+50(200-m)≥9000,求最大整数解即可.
(1)
设A种机器人每台每小时分拣x件包裹,B种机器人每台每小时分拣y件包裹,
根据题意,得
解得,
答:A种机器人每台每小时分拣40件包裹,B种机器人每台每小时分拣50件包裹.
(2)
设购进A种机器人m台,则购进B种机器人(200-m)台.
根据题意,得40m+50(200-m)≥9000,
解得m≤100.
答:最多应购进A种机器人100台.
【点睛】本题考查了一元一次不等式的应用、二元一次方程组的应用,正确理解题意是解题关键.
26.大瓶产品16000瓶,小瓶产品12000瓶
【分析】设这些消毒液应分装大瓶产品瓶,小瓶产品瓶,根据题意列二元一次方程组,求解即可.
【详解】解:设这些消毒液应分装大瓶产品瓶,小瓶产品瓶,
根据题意,得,
解得,
答:这些消毒液应分装大瓶产品16000瓶,小瓶产品12000瓶.
【点睛】本题考查了二元一次方程组的应用,根据题意建立合适的等量关系是解题的关键.
27.每个篮球50元,每副羽毛球拍30元
【分析】设每个篮球元,每副羽毛球拍元,由题意:七年级(1)班购买了3个篮球和4副羽毛球拍共用了270元,七年级(2)班购买了同样的5个篮球和6副羽毛球拍共用了430元,列出二元一次方程组,解方程组即可.
【详解】解:设每个篮球元,每副羽毛球拍元,
根据题意列方程组,得,
解这个方程组,得.
答:每个篮球50元,每副羽毛球拍30元.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
28.A型号设备7万元/台,B型号设备5万元/台
【分析】由题意,设A型号设备x万元/台,B型号设备y万元/台,然后列出方程组,解方程组即可得到答案.
【详解】解:设A型号设备x万元/台,B型号设备y万元/台.
根据题意列方程组,得:
解方程得:.
答:A型号设备7万元/台,B型号设备5万元/台.
【点睛】本题考查了二元一次方程组的应用,解题的关键是熟练掌握题意,正确的理解题意,从而进行解题.
29.甲型物流无人机每架400万元,乙型物流无人机每架5万元
【分析】设甲型物流无人机每架x万元,乙型物流无人机每架y万元,根据“1架甲型物流无人机与7架乙型物流无人机总价为435万元,2架甲型物流无人机与9架乙型物流无人机总价为845万元”即可列出二元一次方程组.
【详解】解:设甲型物流无人机每架x万元,乙型物流无人机每架y万元,
根据题意得,,
解得:,
答:甲型物流无人机每架400万元,乙型物流无人机每架5万元.
【点睛】本题主要考查了二元一次方程组的应用,根据总价找出等量关系是解决问题的关键.
30.一支百合6元,一支康乃馨4元
【分析】设一支百合x 元,一支康乃馨y元,由题意:1支百合和2支康乃馨共14元,2支百合和3支康乃馨共24元.列出二元一次方程组,解方程组即可.
【详解】解:设一支百合x 元,一支康乃馨y元,
依题意得:,
解得:,
答:一支百合6元,一支康乃馨4元.
【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
