人教版七年级数学下册--5.2.2 平行线的判定 课件(共34张PPT)
文档属性
| 名称 | 人教版七年级数学下册--5.2.2 平行线的判定 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 15:43:57 | ||
图片预览









文档简介
(共34张PPT)
5.3 平行线的性质
5.3.1 平行线的性质(第1课时)
人教版 数学 七年级 下册
【思考】根据同位角相等可以判定两直线平行,反过来如果两直线平行,同位角之间有什么关系呢?内错角、同旁内角之间又有什么关系呢?
导入新知
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能够根据平行线的性质进行简单的推理.
学习目标
3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力.
如何判断两条直线是否平行?
(1) 根据定义.
(2) 根据平行公理的推论.
探究新知
知识点1
平行线的判定方法 1、2、3
思考
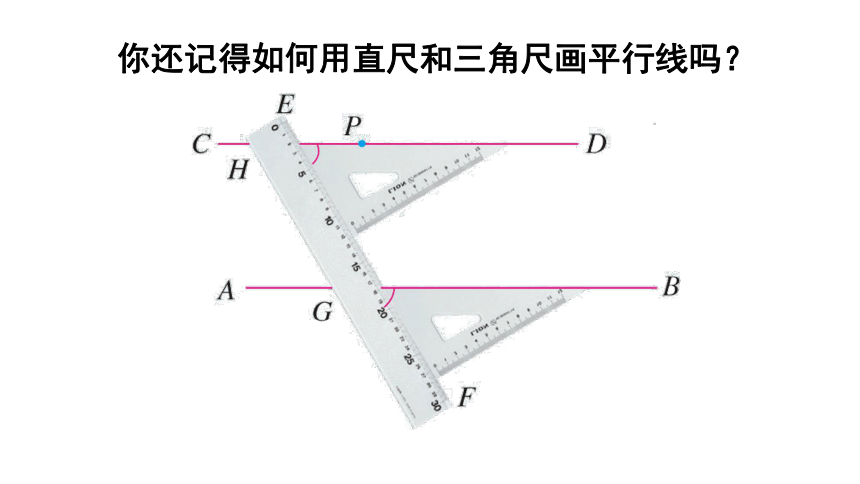
你还记得如何用直尺和三角尺画平行线吗?
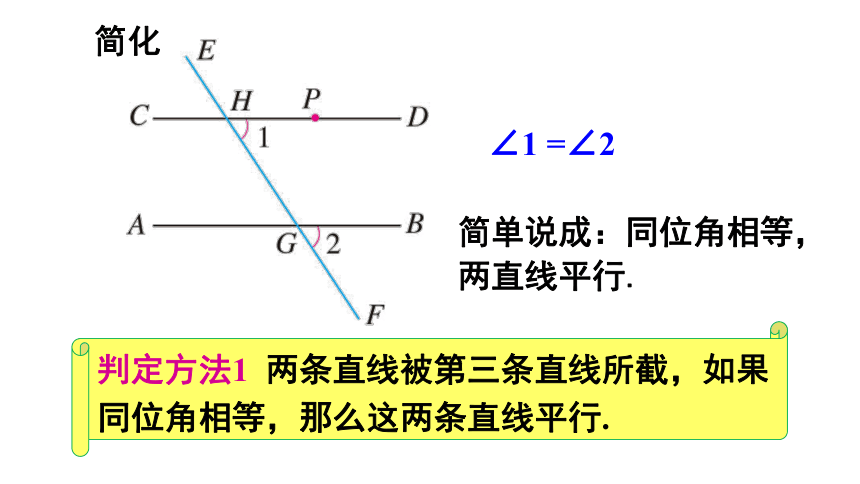
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
∠1 =∠2
简化
同位角相等,两直线平行.
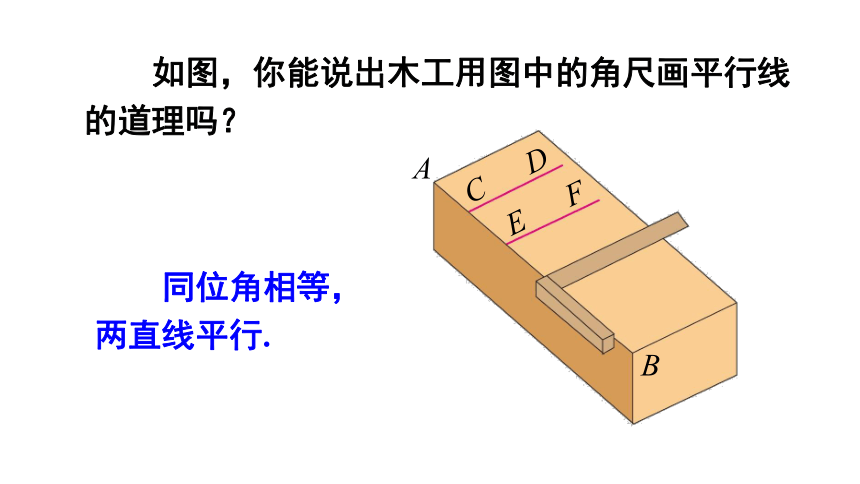
如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?
思考
如图,如果∠2 =∠3,那么 a 与 b 平行吗?
因为∠2 =∠3,∠3 =∠1,
所以∠1 =∠2,
所以 a∥b .
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?
思考
如图,如果∠2 +∠4 = 180°,那么 a 与 b 平行吗?
因为∠2 +∠4 = 180°,
∠1 +∠4 = 180°,
所以∠1 = ∠2,
所以 a∥b .
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
判定方法 1 同位角相等,两直线平行.
判定方法 2 内错角相等,两直线平行.
判定方法 3 同旁内角互补,两直线平行.
平行线的判定
归纳
例 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
知识点2
同一平面内,同垂直于第三条直线的两直线平行
已知条件:直线 b 与直线 c 都垂直于直线 a .
要说明的结论:直线 b 与直线 c 平行吗?
答:直线 b 与直线 c 平行.
理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1 和∠2 是同位角,
∴ b∥c(同位角相等,两直线平行).
你还能用其他方法说明理由吗?
1. 如图, BE 是 AB 的延长线.
(1)由∠CBE =∠A 可以判定哪两条直线平行?根据是什么?
答: AD∥BC . 根据同位角相等,两直线平行.
练习
(2)由∠CBE =∠C 可以判定哪两条直线平行?根据是什么?
答: AE∥CD . 根据内错角相等,两直线平行.
答: AE∥CD . 根据同旁内角互补,两直线平行.
(3)由∠D +∠A = 180°可以判定哪两条直线平行?根据是什么?
2. 在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2 是直角,那么再度量图中已标出的哪个角,就可以判断两条直轨是否平行?为什么?
解:①可度量∠3 的度数,因为∠3 与∠2是同旁内角,若∠3=90°,则∠3+∠2=180°.根据“同旁内角互补,两直线平行”可得两条直轨平行.
②也可度量∠4 的度数,因为∠4 与∠2 是同位角,若∠4=90°,则∠4=∠2. 根据“同位角相等,两直线平行”可得两条直轨平行.
③还可度量∠5 的度数,因为∠5 与∠2 是内错角,若∠5=90°,则∠5=∠2. 根据“内错角相等,两直线平行”可得两条直轨平行.
3.如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横线互相平行吗?你有多少种判别方法?
答:平行 . 理由不唯一.
如图,下列推理正确的有( )
①因为∠2=∠4,所以 AD∥BC;
②因为∠BAD+∠D=180°,所以 AD∥BC;
③因为∠1=∠3,所以 AD∥BC;
④因为∠1+∠2+∠B=180°,所以 AD∥BC.
A.1个 B.2个 C.3个 D.4个
错 解
正 解
A 或 C 或 D
B
误区 不能准确识别截线和被截线,从而误判两直线平行
错因分析
错解错在没有分清截线和被截线.①中∠2 和∠4 的公共边所在的直线(截线)是AC,另外两边所在的直线(被截线)分别是 AB 和 CD,所以由∠2=∠4 得 AB∥CD,所以①错误;同理由∠BAD+∠D=180°,可得 AD∥BC,所以②错误.
错因分析
两条直线位置关系的判定,主要是通过角的关系来实现的.要识别是哪两条直线被第三条直线所截而成的角,要从组成角的两边入手:两个角的公共边所在的直线就是截线,即第三条直线,另外两条边所在的直线就是被截线.正确区分截线和被截线是判断两条直线平行的关键.
如图,将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为( )
A.35° B.45°
C.55° D.65°
C
3
链接中考
1.如图所示,直线a∥b,直线c与直线a,b相交,若∠1=56°,则∠2等于 ( )
A. 24°
B. 34°
C. 56°
D. 124°
C
课堂检测
基础巩固题
1
2
a
c
b
2.如图所示,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
A. ∠EMB=∠END
B. ∠BMN=∠MNC
C. ∠CNH=∠BPG
D. ∠DNG=∠AME
D
课堂检测
3. 如图所示,直线a∥b,点B在直线a上,AB⊥BC,若
∠1=38°,则∠2的度数为 ( )
A. 38° B. 52°
C. 76° D. 142°
B
课堂检测
4.如图所示,AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
A. 60° B. 80° C. 75° D. 70°
D
课堂检测
5. 如图所示,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= °.
70
课堂检测
解: ∵ AB∥DE( ),
∴∠A= ______ ( ).
∵AC∥DF( ),
∴∠D+ _______=180o ( ).
∴∠A+∠D=180o( ).
有这样一道题:如图,若AB∥DE , AC∥DF,试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据.
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
能力提升题
课堂检测
如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3.
∵两直线平行,内错角相等,
∴∠2=∠3.
∴∠1=∠2=∠3=∠4.
∴进入潜望镜的光线和离开潜望镜
的光线平行.
拓广探索题
课堂检测
∵∠1=∠2,∠3=∠4,
∴ ∠5=∠6.
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
课堂小结
5.3 平行线的性质
5.3.1 平行线的性质(第1课时)
人教版 数学 七年级 下册
【思考】根据同位角相等可以判定两直线平行,反过来如果两直线平行,同位角之间有什么关系呢?内错角、同旁内角之间又有什么关系呢?
导入新知
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.
2. 能够根据平行线的性质进行简单的推理.
学习目标
3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力.
如何判断两条直线是否平行?
(1) 根据定义.
(2) 根据平行公理的推论.
探究新知
知识点1
平行线的判定方法 1、2、3
思考
你还记得如何用直尺和三角尺画平行线吗?
判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
∠1 =∠2
简化
同位角相等,两直线平行.
如图,你能说出木工用图中的角尺画平行线的道理吗?
A
B
C D
E F
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢?
思考
如图,如果∠2 =∠3,那么 a 与 b 平行吗?
因为∠2 =∠3,∠3 =∠1,
所以∠1 =∠2,
所以 a∥b .
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢?
思考
如图,如果∠2 +∠4 = 180°,那么 a 与 b 平行吗?
因为∠2 +∠4 = 180°,
∠1 +∠4 = 180°,
所以∠1 = ∠2,
所以 a∥b .
判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
判定方法 1 同位角相等,两直线平行.
判定方法 2 内错角相等,两直线平行.
判定方法 3 同旁内角互补,两直线平行.
平行线的判定
归纳
例 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
知识点2
同一平面内,同垂直于第三条直线的两直线平行
已知条件:直线 b 与直线 c 都垂直于直线 a .
要说明的结论:直线 b 与直线 c 平行吗?
答:直线 b 与直线 c 平行.
理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1 和∠2 是同位角,
∴ b∥c(同位角相等,两直线平行).
你还能用其他方法说明理由吗?
1. 如图, BE 是 AB 的延长线.
(1)由∠CBE =∠A 可以判定哪两条直线平行?根据是什么?
答: AD∥BC . 根据同位角相等,两直线平行.
练习
(2)由∠CBE =∠C 可以判定哪两条直线平行?根据是什么?
答: AE∥CD . 根据内错角相等,两直线平行.
答: AE∥CD . 根据同旁内角互补,两直线平行.
(3)由∠D +∠A = 180°可以判定哪两条直线平行?根据是什么?
2. 在铺设铁轨时,两条直轨必须是互相平行的.如图,已经知道∠2 是直角,那么再度量图中已标出的哪个角,就可以判断两条直轨是否平行?为什么?
解:①可度量∠3 的度数,因为∠3 与∠2是同旁内角,若∠3=90°,则∠3+∠2=180°.根据“同旁内角互补,两直线平行”可得两条直轨平行.
②也可度量∠4 的度数,因为∠4 与∠2 是同位角,若∠4=90°,则∠4=∠2. 根据“同位角相等,两直线平行”可得两条直轨平行.
③还可度量∠5 的度数,因为∠5 与∠2 是内错角,若∠5=90°,则∠5=∠2. 根据“内错角相等,两直线平行”可得两条直轨平行.
3.如图,这是小明同学自己制作的英语抄写纸的一部分,其中的横线互相平行吗?你有多少种判别方法?
答:平行 . 理由不唯一.
如图,下列推理正确的有( )
①因为∠2=∠4,所以 AD∥BC;
②因为∠BAD+∠D=180°,所以 AD∥BC;
③因为∠1=∠3,所以 AD∥BC;
④因为∠1+∠2+∠B=180°,所以 AD∥BC.
A.1个 B.2个 C.3个 D.4个
错 解
正 解
A 或 C 或 D
B
误区 不能准确识别截线和被截线,从而误判两直线平行
错因分析
错解错在没有分清截线和被截线.①中∠2 和∠4 的公共边所在的直线(截线)是AC,另外两边所在的直线(被截线)分别是 AB 和 CD,所以由∠2=∠4 得 AB∥CD,所以①错误;同理由∠BAD+∠D=180°,可得 AD∥BC,所以②错误.
错因分析
两条直线位置关系的判定,主要是通过角的关系来实现的.要识别是哪两条直线被第三条直线所截而成的角,要从组成角的两边入手:两个角的公共边所在的直线就是截线,即第三条直线,另外两条边所在的直线就是被截线.正确区分截线和被截线是判断两条直线平行的关键.
如图,将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为( )
A.35° B.45°
C.55° D.65°
C
3
链接中考
1.如图所示,直线a∥b,直线c与直线a,b相交,若∠1=56°,则∠2等于 ( )
A. 24°
B. 34°
C. 56°
D. 124°
C
课堂检测
基础巩固题
1
2
a
c
b
2.如图所示,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
A. ∠EMB=∠END
B. ∠BMN=∠MNC
C. ∠CNH=∠BPG
D. ∠DNG=∠AME
D
课堂检测
3. 如图所示,直线a∥b,点B在直线a上,AB⊥BC,若
∠1=38°,则∠2的度数为 ( )
A. 38° B. 52°
C. 76° D. 142°
B
课堂检测
4.如图所示,AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
A. 60° B. 80° C. 75° D. 70°
D
课堂检测
5. 如图所示,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= °.
70
课堂检测
解: ∵ AB∥DE( ),
∴∠A= ______ ( ).
∵AC∥DF( ),
∴∠D+ _______=180o ( ).
∴∠A+∠D=180o( ).
有这样一道题:如图,若AB∥DE , AC∥DF,试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据.
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
能力提升题
课堂检测
如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3.
∵两直线平行,内错角相等,
∴∠2=∠3.
∴∠1=∠2=∠3=∠4.
∴进入潜望镜的光线和离开潜望镜
的光线平行.
拓广探索题
课堂检测
∵∠1=∠2,∠3=∠4,
∴ ∠5=∠6.
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
课堂小结
