2014年新人教版八年级数学下18.2.1矩形(第1课时)课件ppt
文档属性
| 名称 | 2014年新人教版八年级数学下18.2.1矩形(第1课时)课件ppt |  | |
| 格式 | zip | ||
| 文件大小 | 253.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 17:32:01 | ||
图片预览

文档简介
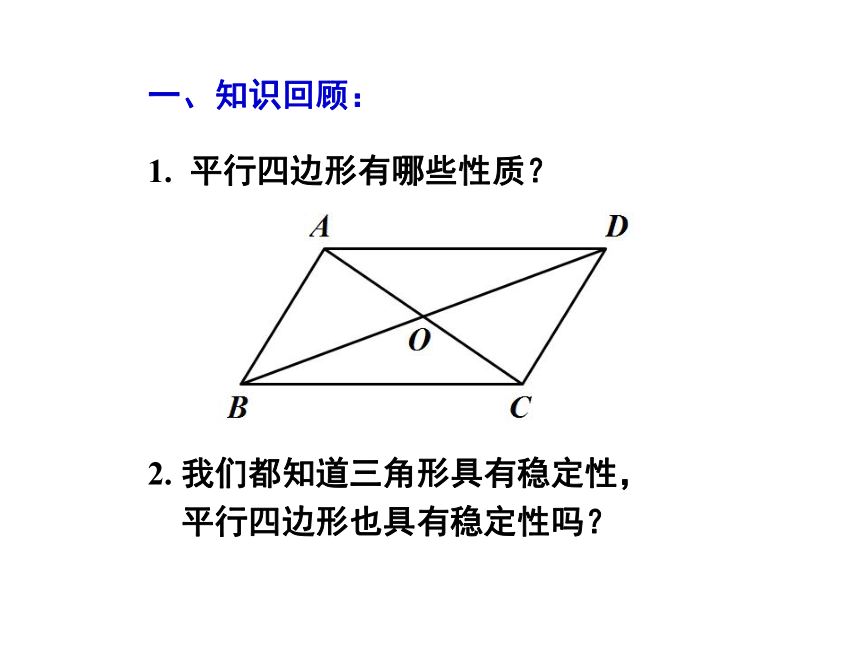
课件16张PPT。第十八章 平行四边形zx``x``k18.2.1 矩形(一)一、知识回顾:1. 平行四边形有哪些性质?2. 我们都知道三角形具有稳定性,
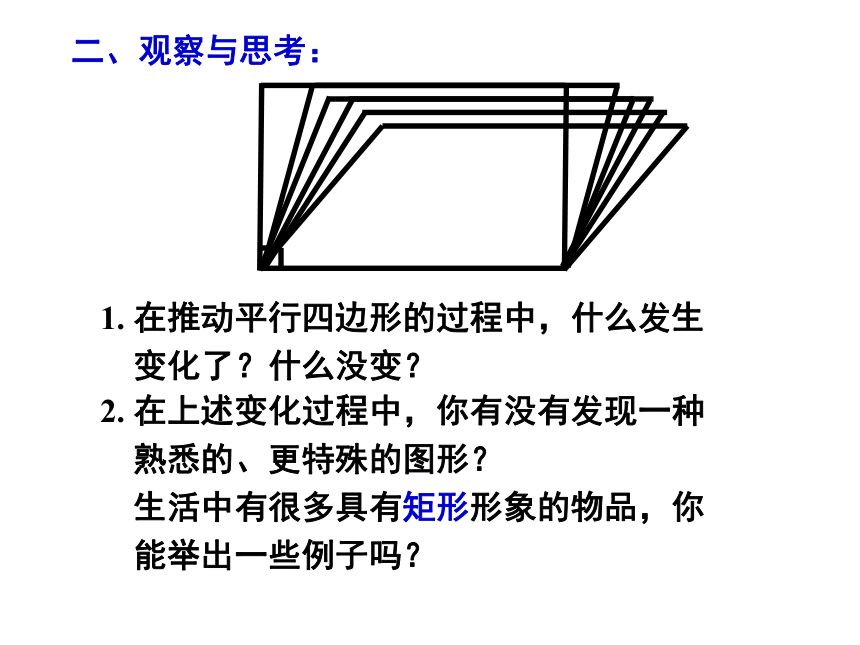
平行四边形也具有稳定性吗?二、观察与思考:1. 在推动平行四边形的过程中,什么发生
变化了?什么没变?2. 在上述变化过程中,你有没有发现一种
熟悉的、更特殊的图形?
生活中有很多具有矩形形象的物品,你
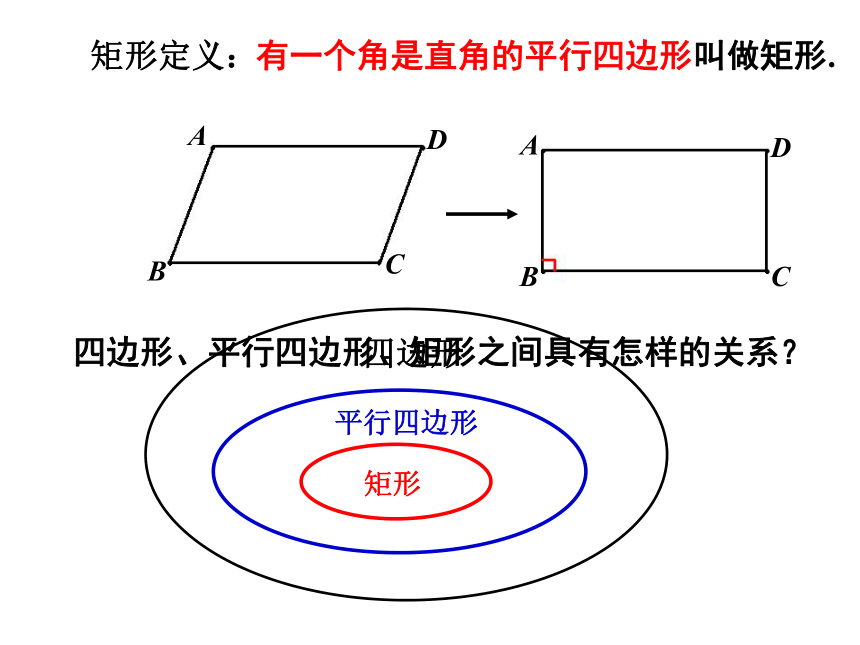
能举出一些例子吗?Z```x``xk有一个角是直角的平行四边形叫做矩形.四边形平行四边形矩形矩形定义:四边形、平行四边形、矩形之间具有怎样的关系?三、合作探究:
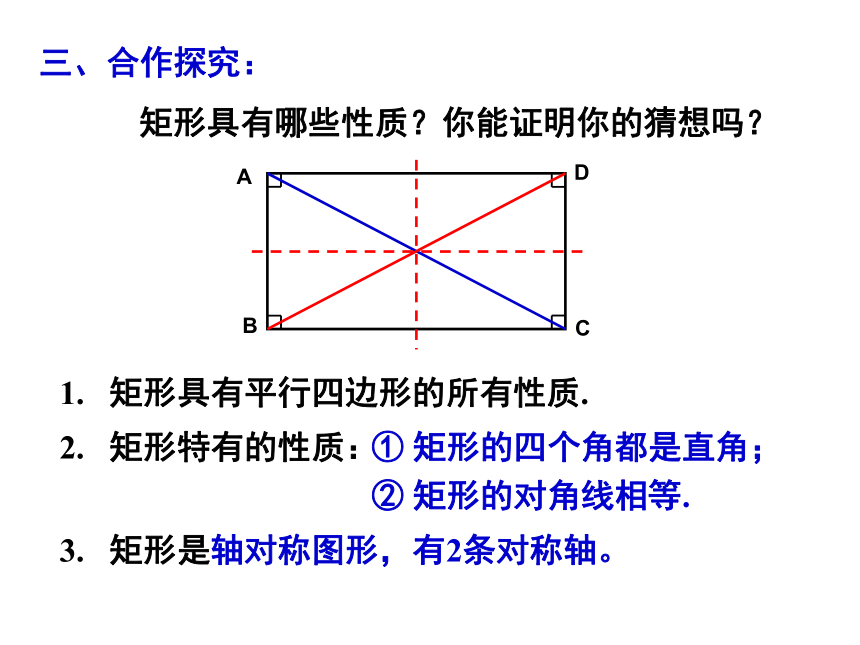
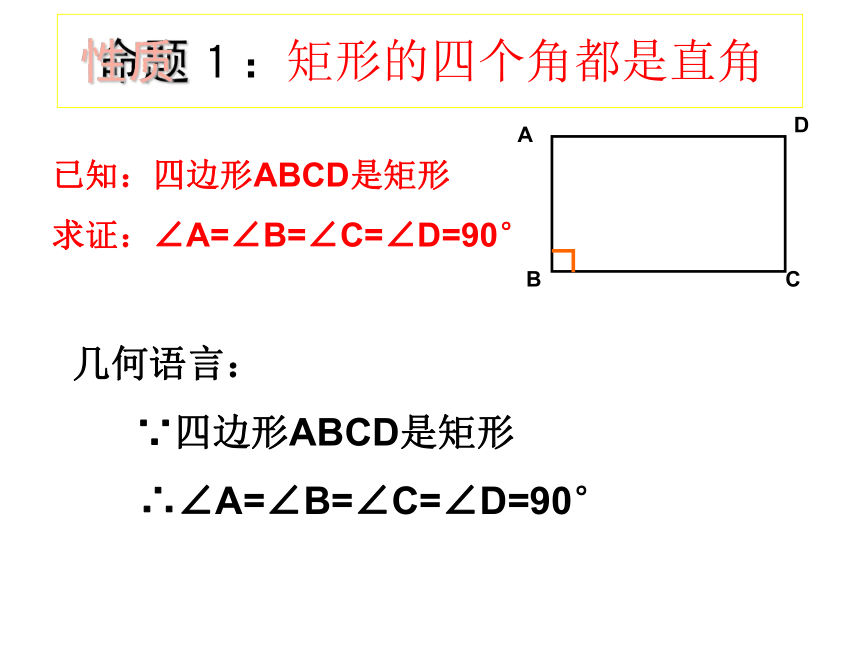
矩形具有哪些性质?你能证明你的猜想吗?1. 矩形具有平行四边形的所有性质.2. 矩形特有的性质:① 矩形的四个角都是直角;② 矩形的对角线相等.3. 矩形的对称性:3. 矩形是轴对称图形,有2条对称轴。ABCD 1:矩形的四个角都是直角已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°DCBA几何语言:
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°命题性质ABCD几何语言:
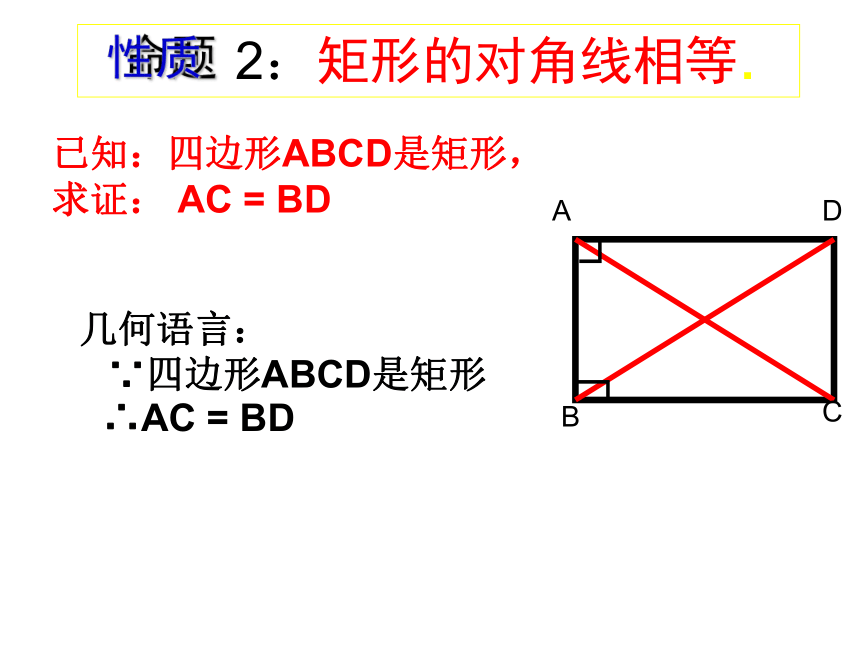
∵四边形ABCD是矩形∴AC = BD 2:矩形的对角线相等.命题性质已知:四边形ABCD是矩形,
求证: AC = BD ◆ 两对全等的等腰三角形.你在矩形中还发现了哪些基本图形?◆ 四个全等的直角三角形.你在矩形中还发现了哪些基本图形?你在矩形中还发现了哪些基本图形?◆ 两对全等的等腰三角形. ````zx``xk◆ 四个全等的直角三角形.四、思考:
观察矩形中的Rt△ABC,
在Rt△ABC中,BO是
斜边AC上的中线,BO
与AC有什么关系? 根据矩形的性质,可以得到:归纳:直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.例 如图,矩形ABCD的两条对角线AC,BD相交于点O,∠AOB=60°,AB=4.
求矩形对角线的长.练习: 如图,把矩形纸片ABCD沿对角线AC
折叠,点B落在点E处,EC与AD相交于点F.
(1)求证:△FAC是等腰三角形;
(2)若AB=4,BC=6,求△FAC的周长和
面积.五、课堂小结1. 什么叫矩形?
矩形有哪些性质? 有一个角是直角的平行四边形叫做矩形. 对边平行且相等对角相等对角线互相平分 对角线相等且
互相平分四个角都是直角对边平行且相等课堂小结2. 解题策略:
矩形的问题经常转化到等腰三角形或直角三角形中解决. 2. 如图,在矩形ABCD中,AB=8,对角线BD比AD长4.求:① AD的长;
② 点A到BD的距离
AE的长. 作业:
1. 教材练习第1、2题.
平行四边形也具有稳定性吗?二、观察与思考:1. 在推动平行四边形的过程中,什么发生
变化了?什么没变?2. 在上述变化过程中,你有没有发现一种
熟悉的、更特殊的图形?
生活中有很多具有矩形形象的物品,你
能举出一些例子吗?Z```x``xk有一个角是直角的平行四边形叫做矩形.四边形平行四边形矩形矩形定义:四边形、平行四边形、矩形之间具有怎样的关系?三、合作探究:
矩形具有哪些性质?你能证明你的猜想吗?1. 矩形具有平行四边形的所有性质.2. 矩形特有的性质:① 矩形的四个角都是直角;② 矩形的对角线相等.3. 矩形的对称性:3. 矩形是轴对称图形,有2条对称轴。ABCD 1:矩形的四个角都是直角已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°DCBA几何语言:
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°命题性质ABCD几何语言:
∵四边形ABCD是矩形∴AC = BD 2:矩形的对角线相等.命题性质已知:四边形ABCD是矩形,
求证: AC = BD ◆ 两对全等的等腰三角形.你在矩形中还发现了哪些基本图形?◆ 四个全等的直角三角形.你在矩形中还发现了哪些基本图形?你在矩形中还发现了哪些基本图形?◆ 两对全等的等腰三角形. ````zx``xk◆ 四个全等的直角三角形.四、思考:
观察矩形中的Rt△ABC,
在Rt△ABC中,BO是
斜边AC上的中线,BO
与AC有什么关系? 根据矩形的性质,可以得到:归纳:直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半.例 如图,矩形ABCD的两条对角线AC,BD相交于点O,∠AOB=60°,AB=4.
求矩形对角线的长.练习: 如图,把矩形纸片ABCD沿对角线AC
折叠,点B落在点E处,EC与AD相交于点F.
(1)求证:△FAC是等腰三角形;
(2)若AB=4,BC=6,求△FAC的周长和
面积.五、课堂小结1. 什么叫矩形?
矩形有哪些性质? 有一个角是直角的平行四边形叫做矩形. 对边平行且相等对角相等对角线互相平分 对角线相等且
互相平分四个角都是直角对边平行且相等课堂小结2. 解题策略:
矩形的问题经常转化到等腰三角形或直角三角形中解决. 2. 如图,在矩形ABCD中,AB=8,对角线BD比AD长4.求:① AD的长;
② 点A到BD的距离
AE的长. 作业:
1. 教材练习第1、2题.
