【江苏版】2014届中考数学专题(12)探索性问题
文档属性
| 名称 | 【江苏版】2014届中考数学专题(12)探索性问题 |
|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 00:00:00 | ||
图片预览





文档简介
( http: / / www.21cnjy.com )
选择题
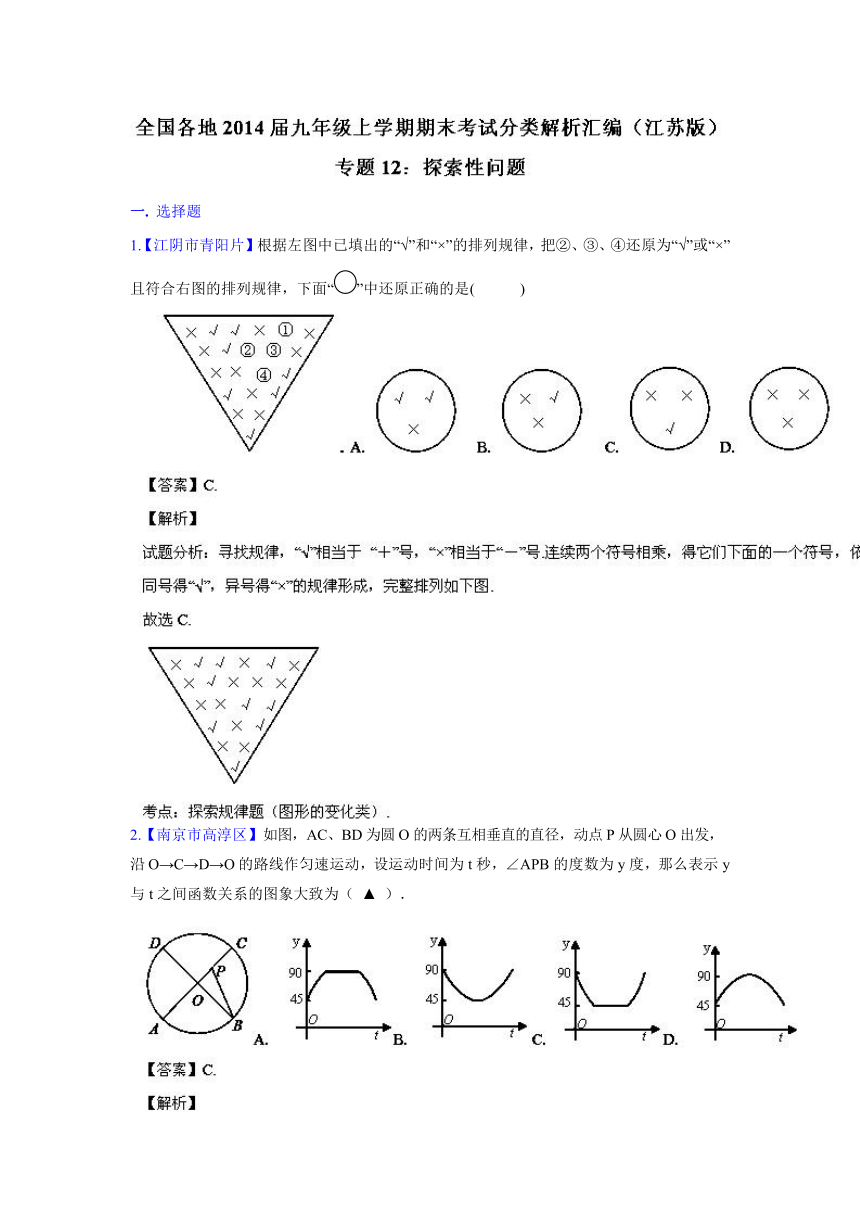
1.【江阴市青阳片】根据左图中已填出的“ ( http: / / www.21cnjy.com )√”和“×”的排列规律,把②、③、④还原为“√”或“×”且符合右图的排列规律,下面“”中还原正确的是( )
( http: / / www.21cnjy.com )2.【南京市高淳区】如图,AC、BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( ▲ ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )3.【无锡市惠山北片】定义:,,例如,,则等于 ( )
A.(-6,5) B.(-5,6) C.(6,-5) D.(-5,6)
( http: / / www.21cnjy.com )
4.【扬州市邗江区】如图,已知抛物线 HYPERLINK "http://www.21cnjy.com" 和直线 HYPERLINK "http://www.21cnjy.com" .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.下列判断: ①当x>2时,M=y2; ②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x= 1 .其中正确的有 ( )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
5.【无锡市前洲中学】一只跳蚤在第一象限及 ( http: / / www.21cnjy.com )x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第2014秒时跳蚤所在位置的坐标是( )
A.(0,672 ) B.(672,0) C.(44,10) D.(10,44)
( http: / / www.21cnjy.com )二。填空题
1.【无锡市滨湖中学】已知二次函数y=ax ( http: / / www.21cnjy.com )2+bx+c(a≠0)的图象如图所示,给出以下4个结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0.其中正确的结论有__________________.(填写序号)
( http: / / www.21cnjy.com )
2.【兴化市茅山中心校】已 ( http: / / www.21cnjy.com )知集合A中的数与集合B中对应的数之间的关系是某个二次函数.若用x表示集合A中的数,用y表示集合B中的数,由于粗心,小聪算错了集合B中的一个y值,请你指出这个算错的y值为 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
3.【兴化市茅山中心校】如图,利用两面 ( http: / / www.21cnjy.com )夹角为135°且足够长的墙,围成梯形围栏ABCD,∠C=90°,新建墙BCD总长为15米,则当CD= 米时,梯形围栏的面积为36平方米.
( http: / / www.21cnjy.com )∴梯形ABCD面积S=(AD+BC) CD=(15-2x+15-x) x=36
解得:x1=4,x2=6
考点: 一元二次方程的应用.
4.【兴化市茅山中心校】如图,在等 ( http: / / www.21cnjy.com )腰Rt△ABC中,∠A=90°,AC=7,点O在AC上,且AO=2,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转90°,得到线段OD,要使点D恰好落在BC上,则AP的长等于 .
( http: / / www.21cnjy.com )5.【江阴市青阳片】读一读:式子“1+2+3+4+……+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,这里“ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ”是求和符号,通过以上材料的阅读,计算 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =
( http: / / www.21cnjy.com )
6.【南京市高淳区】某公园草坪的防 ( http: / / www.21cnjy.com )护栏形状是抛物线形.为了牢固起见,每段护栏按0.4m的间距加装不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则其中防护栏支柱A2B2的长度为 ▲ m.
( http: / / www.21cnjy.com )7.【南京市高淳区】如图,点A、B在直线MN上,AB=8cm,⊙A、⊙B的半径均为1cm.⊙A以每秒1cm的速度自左向右运动;与此同时,⊙B的半径也随之增大,其半径r(cm)与时间t(秒)之间满足关系式r=1+t(t≥0) .则当点A出发后 ▲ 秒,两圆相切.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )8.【无锡市惠山北片】设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是 .(填写所有正确结论的序号)
①[0)=0 ②[x)-x的最小值是0 ③[x)-x的最大值是0 ④存在实数x,使[x)-x=0.5成立.
( http: / / www.21cnjy.com )
9.【扬州市邗江区】我们知道,一元二次方程 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 没有实数根,即不存在一个实数的平方等于 ( http: / / www.21cnjy.com ).若我们规定一个新数“ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ”,使其满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (即方程 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 有一个根为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,从而对于任意正整数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,我们可以得到 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 同理可得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .那么 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值为 .
( http: / / www.21cnjy.com )三。解答题
1.【无锡市滨湖中学】某公司销售一种新型节能电子小产品,现准备从国内和国外两种销售方案中选择一种进行销售:①若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y =- HYPERLINK "http://www.21cnjy.com" x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 HYPERLINK "http://www.21cnjy.com" x2元的附加费,月利润为W外(元).
(1)若只在国内销售,当x=1000(件)时,y= (元/件);
(2)分别求出W内、W外与x间的函数关系式(不必写x的取值范围);
(3)若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
2.【泰州市姜堰区】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
( http: / / www.21cnjy.com )
3.【无锡市滨湖中学】探究一:如图1,已知正 ( http: / / www.21cnjy.com )方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.
( http: / / www.21cnjy.com )
探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出 HYPERLINK "http://www.21cnjy.com" 的值.
( http: / / www.21cnjy.com )
探究三:小明思考这样一个问 ( http: / / www.21cnjy.com )题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
∵AB=GM=3,FN=BC=4,
∴;
( http: / / www.21cnjy.com )
4.【兴化市茅山中心校】如图, AB是⊙O的直径,点C在⊙O上,D是AB延长线上的一点,AE⊥DC交DC的延长线于E,AC平分∠DAE.
(1)直线DE与⊙O有怎样的位置关系?为什么?
(2)若AC=,⊙O的半径为1,求CD的长及由弧BC、线段BD、CD所围成的阴影部分的面积.
( http: / / www.21cnjy.com )∵DC=AC,∠CAB=30°,
( http: / / www.21cnjy.com )
(2)连接BC.
∵AB是⊙O的直径,
( http: / / www.21cnjy.com )
5.【兴化市茅山中心校】 ( http: / / www.21cnjy.com )如图,在△ABC中,∠C=90°,CD⊥AB,垂足为D,AC=20,BC=15.动点P从A开始,以每秒2个单位长的速度沿AB方向向终点B运动,过点P分别作AC、BC边的垂线,垂足为E、F.
(1)求AB与CD的长;
(2)当矩形PECF的面积最大时,求点P运动的时间t;
(3)以点C为圆心,r为半径画圆,若圆C与斜边AB有且只有一个公共点时,求r的取值范围.
( http: / / www.21cnjy.com )
∴
(2)∵△APE∽△ABC,
( http: / / www.21cnjy.com )
6.【江阴市青阳片】如图①,梯形ABC ( http: / / www.21cnjy.com )D中,∠C=90°.动点E、F同时从点B出发,点E沿折线 BA—AD—DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1 cm/s.设E、F出发t s时,△EBF的面积为y cm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.请根据图中的信息,解答下列问题:
(1)梯形上底的长AD=_____cm,梯形ABCD的面积_____cm2;
(2)当点E在BA、DC上运动时,分别求出y与t的函数关系式(注明自变量的取值范围);
(3)当t为何值时,△EBF与梯形ABCD的面积之比为1:2.
( http: / / www.21cnjy.com )试题解析:(1)2,14.
( http: / / www.21cnjy.com )7.【江阴市青阳片】小明遇到这样一个问题:如图1,在边长为啊a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积;
小明发现:分别延长QE,MF,NG,P ( http: / / www.21cnjy.com )H,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
( http: / / www.21cnjy.com )
请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积;
参考小明思考问题的方法,解决问题:
(3)如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则AD的长为__________.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )8.【靖江市】如图所示,在梯形ABCD中,AD∥BC,∠BDC=90°,E为DC上一点,∠BDE=∠DBC.
(1)求证: DE=CE;
(2)若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 \* MERGEFORMAT ,试判断四边形ABED的形状,并说明理由.
( http: / / www.21cnjy.com )∵ HYPERLINK "http://www.21cnjy.com" ,∴AD=BE.
( http: / / www.21cnjy.com )
9.【靖江市】在平面直角坐标系xOy中,二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象过A(-1,-2)、 B(1,0)两点.
(1)求此二次函数的解析式并画出二次函数图象;
(2)点P(t,0)是x轴上的一个 ( http: / / www.21cnjy.com )动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
( http: / / www.21cnjy.com )作图如下:
( http: / / www.21cnjy.com )
10.【靖江市】已知⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为( HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 \* MERGEFORMAT ,0), HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 CAB=90°, AC=AB,顶点A在⊙O上运动.
(1)设点A的横坐标为x,△ABC的面积 ( http: / / www.21cnjy.com )为S,求S与x之间的函数关系式,并求出S的最大值与最小值;(2)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
( http: / / www.21cnjy.com )AB的长,进而求出面积的表达式,结合定义域,根据一次函数的性质确定最大最小值;
( http: / / www.21cnjy.com )②当点A位于第四象限时(如图2),点A的坐标为(,),
( http: / / www.21cnjy.com )12.【靖江市】如图,抛物线过x轴上两点A(9,0) , C(-3,0), 且与y轴交于点B(0,-12).
(1)求抛物线的解析式;
(2)若动点P从点A出发,以每秒2个 ( http: / / www.21cnjy.com )单位沿射线AC方向运动;同时,点Q从点B出发,以每秒1个单位沿射线BA方向运动,当点P到达点C处时,两点同时停止运动.问当t为何值时,△APQ∽△AOB?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBNA面积的最大值.
( http: / / www.21cnjy.com )又∵AC=12,∴0≤t≤6.
∵△APQ∽△AOB,∴ HYPERLINK "http://www.21cnjy.com" ,即 HYPERLINK "http://www.21cnjy.com" ,解得 HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )13.【南京市高淳区】如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.
(1)当t为何值时,△PBQ是直角三角形
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为x cm,试求y与x的函数关系式.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )(2)①过P作PH⊥BC,在Rt△PHB中,BP=4-t ,PH= HYPERLINK "http://www.21cnjy.com" ,
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
14.【无锡市塔影中学】一家图文广告公 ( http: / / www.21cnjy.com )司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
画板的边长(dm) 10 20
出售价(元/张) 160 220
(1)求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
15.【无锡市塔影中学】如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
(1)如图2,⊙O与Rt△AB ( http: / / www.21cnjy.com )C的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的 ( http: / / www.21cnjy.com )动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )∴y=;
③如图4,
( http: / / www.21cnjy.com )
16.【无锡市塔影中学】在平面直角坐标系中 ( http: / / www.21cnjy.com ),O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
( http: / / www.21cnjy.com )确定出解析式;
( http: / / www.21cnjy.com )∴OB=AB,BC=BD,
( http: / / www.21cnjy.com ) HYPERLINK "http://www.21cnjy.com"
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
17.【无锡市惠山北片】翻转 ( http: / / www.21cnjy.com )类的计算问题在全国各地的中考试卷中出现的频率很大,因此初三(5)班聪慧的小菲同学结合2011年苏州市数学中考卷的倒数第二题对这类问题进行了专门的研究。你能和小菲一起解决下列各问题吗?(以下各问只要求写出必要的计算过程和简洁的文字说明即可。)
(1)如图①,小菲同学把一个边长为1的 ( http: / / www.21cnjy.com )正三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片向右翻转一周回到初始位置,求顶点O所经过的路程;并求顶点O所经过的路线;
(2)小菲进行类比研究:如图②,她把边 ( http: / / www.21cnjy.com )长为1的正方形纸片OABC放在直线l2上,OA边与直线l2重合,然后将正方形纸片向右翻转若干次.她提出了如下问题:
问题①:若正方形纸片OABC接上述方法翻转一周回到初始位置,求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 。
(3)①小菲又进行了进一步的拓展研究,若 ( http: / / www.21cnjy.com )把这个正三角形的一边OA与这个正方形的一边OA重合(如图3),然后让这个正三角形在正方形上翻转,直到正三角形第一次回到初始位置(即OAB的相对位置和初始时一样),求顶点O所经过的总路程。
②若把边长为1的正方形OABC放在边 ( http: / / www.21cnjy.com )长为1的正五边形OABCD上翻转(如图④),直到正方形第一次回到初始位置,求顶点O所经过的总路程。
(4)规律总结,边长相等的两个正多边 ( http: / / www.21cnjy.com )形,其中一个在另一个上翻转,当翻转后第一次回到初始位置时,该正多边形翻转的次数一定是两正多边形边数的___________。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )18.【无锡市惠山北片】如图,二次函数的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标:
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
( http: / / www.21cnjy.com )试题解析:(1)(﹣3,4);
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
19.【扬州市邗江区】如图①,已知线段 ( http: / / www.21cnjy.com )AB=8,以AB为直径作半圆O,再以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D。
(1)判断线段AP与PD的大小关系,并说明理由;
(2)连接PC,当∠ACP=600时,求弧AD的长;
(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.
( http: / / www.21cnjy.com )又∵OA=OD,∴AP=PD.
( http: / / www.21cnjy.com )
连接OP,同①可得,△APO∽△AED.∴ HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )际问题列函数关系式;8.相似三角形的判定和性质;9.分类思想的应用.
20.【扬州市邗江区】如图,抛物线 HYPERLINK "http://www.21cnjy.com" 与x轴交于点A(—2,0),交y轴于点B(0, HYPERLINK "http://www.21cnjy.com" ).直 HYPERLINK "http://www.21cnjy.com" 过点A与y轴交于点C,与抛物线的另一个交点是D.
(1)求抛物线 HYPERLINK "http://www.21cnjy.com" 与直线 HYPERLINK "http://www.21cnjy.com" 的解析式;
(2)设点P是直线AD下方的抛物线上一动 ( http: / / www.21cnjy.com )点(不与点A、D重合),过点P作 y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m与x的函数关系式,并求出m的最大值.
( http: / / www.21cnjy.com )试题解析:(1)∵ HYPERLINK "http://www.21cnjy.com" 经过点A(—2,0)和B(0, HYPERLINK "http://www.21cnjy.com" )
( http: / / www.21cnjy.com )
当x=2时,y=—3; 当x=4时,y= HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )∴ HYPERLINK "http://www.21cnjy.com" ,即 HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )21.【泰州市姜堰区】正常水位时,抛物线拱桥下的水面宽为BC=20m,水面上升3m达到该地警戒水位DE时,桥下水面宽为10m. 若以BC所在直线为x轴,BC的垂直平分线为y轴,建立如图所示的平面直角坐标系.
(1)求桥孔抛物线的函数关系式;
(2)如果水位以0.2m/h的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没;
(3)当达到警戒水位时,一艘装有防汛器材的船,露出水面部分的宽为4m,高为0.75m,通过计算说明该船能否顺利通过此拱桥?
( http: / / www.21cnjy.com )22.【泰州市姜堰区】如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P,Q分别从O、B两点同时出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,设动点P、Q运动时间为t(单位:s)
(1)当t为何值时,四边形PABQ是平行四边形,请写出推理过程;
(2)通过推理论证:在P、Q的运动过程中,线段DE的长度不变;
( http: / / www.21cnjy.com )23.【泰州市姜堰区】如图,在⊙O中,AB为⊙O的直径,AC为弦,OC=4,∠OAC=60°.
(1)求∠AOC的度数;
(2)在图(1)中,P为直径BA的延长线上一点,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,求证:PC为⊙O的切线.
(3)如图(2),一动点M从A点出发,在⊙O上按逆时针方向运动一周(点M不与点C重合),当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,求动点M所经过的弧长.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为 HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )24.【泰州市姜堰区】已知,关于x的二次函数, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (k为正整数).
(1)若二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象与x轴有两个交点,求k的值.
(2)若关于x的一元二次方程 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.
(3)将(2)中的抛物线平移,当顶 ( http: / / www.21cnjy.com )点至原点时,直线y=2x+b交抛物线于A(-1,n)、B(2,t)两点,问在y轴上是否存在一点C,使得△ABC的内心在y轴上.若存在,求出点C的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )即为所求C点,坐标为(0,-4).
考点: 1. 二次函数的图象与x轴交点问题;2. 一元二次方程根的判别式;3. 二次函数与不等式组;4.轴对称的应用.
25.【无锡市前洲中学】如图,一条抛 ( http: / / www.21cnjy.com )物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,OA=5,AB=2.点E在线段OC上,作∠MEN=∠AOC,使∠MEN的一边始终经过点A,另一边交线段BC于点F,连接AF.
(1)求抛物线的解析式;
(2)当点F是BC的中点时,求点E的坐标;
(3)当△AEF是等腰三角形时,求点E的坐标.
( http: / / www.21cnjy.com )从而点E的坐标为(,0)
(3)由(2)中相似还可知AO:EC=AE:EF,若△AEF为等腰三角形,则有三种可能.
( http: / / www.21cnjy.com )
26.【无锡市前洲中学】如图①,正方形 ( http: / / www.21cnjy.com )ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A B C D匀速运动,同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,设运动的时间为t秒.
(1)当P点在边AB上运动时 ( http: / / www.21cnjy.com ),点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)如果点P、Q保持原速 ( http: / / www.21cnjy.com )度不变,当点P沿A B C D匀速运动时,OP与PQ能否相等?若能,求出所有符合条件的t的值;若不能,请说明理由.
( http: / / www.21cnjy.com )设△OPQ的面积为S,计算可得答案.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
E
选择题
1.【江阴市青阳片】根据左图中已填出的“ ( http: / / www.21cnjy.com )√”和“×”的排列规律,把②、③、④还原为“√”或“×”且符合右图的排列规律,下面“”中还原正确的是( )
( http: / / www.21cnjy.com )2.【南京市高淳区】如图,AC、BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( ▲ ).
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )3.【无锡市惠山北片】定义:,,例如,,则等于 ( )
A.(-6,5) B.(-5,6) C.(6,-5) D.(-5,6)
( http: / / www.21cnjy.com )
4.【扬州市邗江区】如图,已知抛物线 HYPERLINK "http://www.21cnjy.com" 和直线 HYPERLINK "http://www.21cnjy.com" .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.下列判断: ①当x>2时,M=y2; ②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x= 1 .其中正确的有 ( )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
5.【无锡市前洲中学】一只跳蚤在第一象限及 ( http: / / www.21cnjy.com )x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后接着按图中箭头所示方向跳动[即(0,0)→(0,1) →(1,1) →(1,0)→…],且每秒跳动一个单位,那么第2014秒时跳蚤所在位置的坐标是( )
A.(0,672 ) B.(672,0) C.(44,10) D.(10,44)
( http: / / www.21cnjy.com )二。填空题
1.【无锡市滨湖中学】已知二次函数y=ax ( http: / / www.21cnjy.com )2+bx+c(a≠0)的图象如图所示,给出以下4个结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0.其中正确的结论有__________________.(填写序号)
( http: / / www.21cnjy.com )
2.【兴化市茅山中心校】已 ( http: / / www.21cnjy.com )知集合A中的数与集合B中对应的数之间的关系是某个二次函数.若用x表示集合A中的数,用y表示集合B中的数,由于粗心,小聪算错了集合B中的一个y值,请你指出这个算错的y值为 .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
3.【兴化市茅山中心校】如图,利用两面 ( http: / / www.21cnjy.com )夹角为135°且足够长的墙,围成梯形围栏ABCD,∠C=90°,新建墙BCD总长为15米,则当CD= 米时,梯形围栏的面积为36平方米.
( http: / / www.21cnjy.com )∴梯形ABCD面积S=(AD+BC) CD=(15-2x+15-x) x=36
解得:x1=4,x2=6
考点: 一元二次方程的应用.
4.【兴化市茅山中心校】如图,在等 ( http: / / www.21cnjy.com )腰Rt△ABC中,∠A=90°,AC=7,点O在AC上,且AO=2,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转90°,得到线段OD,要使点D恰好落在BC上,则AP的长等于 .
( http: / / www.21cnjy.com )5.【江阴市青阳片】读一读:式子“1+2+3+4+……+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,这里“ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ”是求和符号,通过以上材料的阅读,计算 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =
( http: / / www.21cnjy.com )
6.【南京市高淳区】某公园草坪的防 ( http: / / www.21cnjy.com )护栏形状是抛物线形.为了牢固起见,每段护栏按0.4m的间距加装不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则其中防护栏支柱A2B2的长度为 ▲ m.
( http: / / www.21cnjy.com )7.【南京市高淳区】如图,点A、B在直线MN上,AB=8cm,⊙A、⊙B的半径均为1cm.⊙A以每秒1cm的速度自左向右运动;与此同时,⊙B的半径也随之增大,其半径r(cm)与时间t(秒)之间满足关系式r=1+t(t≥0) .则当点A出发后 ▲ 秒,两圆相切.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )8.【无锡市惠山北片】设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是 .(填写所有正确结论的序号)
①[0)=0 ②[x)-x的最小值是0 ③[x)-x的最大值是0 ④存在实数x,使[x)-x=0.5成立.
( http: / / www.21cnjy.com )
9.【扬州市邗江区】我们知道,一元二次方程 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 没有实数根,即不存在一个实数的平方等于 ( http: / / www.21cnjy.com ).若我们规定一个新数“ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ”,使其满足 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (即方程 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 有一个根为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,从而对于任意正整数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,我们可以得到 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 同理可得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .那么 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值为 .
( http: / / www.21cnjy.com )三。解答题
1.【无锡市滨湖中学】某公司销售一种新型节能电子小产品,现准备从国内和国外两种销售方案中选择一种进行销售:①若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y =- HYPERLINK "http://www.21cnjy.com" x+150,成本为20元/件,月利润为W内(元);②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳 HYPERLINK "http://www.21cnjy.com" x2元的附加费,月利润为W外(元).
(1)若只在国内销售,当x=1000(件)时,y= (元/件);
(2)分别求出W内、W外与x间的函数关系式(不必写x的取值范围);
(3)若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
2.【泰州市姜堰区】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为x m,窗户的透光面积为y m2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.
( http: / / www.21cnjy.com )
3.【无锡市滨湖中学】探究一:如图1,已知正 ( http: / / www.21cnjy.com )方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.
( http: / / www.21cnjy.com )
探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出 HYPERLINK "http://www.21cnjy.com" 的值.
( http: / / www.21cnjy.com )
探究三:小明思考这样一个问 ( http: / / www.21cnjy.com )题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
∵AB=GM=3,FN=BC=4,
∴;
( http: / / www.21cnjy.com )
4.【兴化市茅山中心校】如图, AB是⊙O的直径,点C在⊙O上,D是AB延长线上的一点,AE⊥DC交DC的延长线于E,AC平分∠DAE.
(1)直线DE与⊙O有怎样的位置关系?为什么?
(2)若AC=,⊙O的半径为1,求CD的长及由弧BC、线段BD、CD所围成的阴影部分的面积.
( http: / / www.21cnjy.com )∵DC=AC,∠CAB=30°,
( http: / / www.21cnjy.com )
(2)连接BC.
∵AB是⊙O的直径,
( http: / / www.21cnjy.com )
5.【兴化市茅山中心校】 ( http: / / www.21cnjy.com )如图,在△ABC中,∠C=90°,CD⊥AB,垂足为D,AC=20,BC=15.动点P从A开始,以每秒2个单位长的速度沿AB方向向终点B运动,过点P分别作AC、BC边的垂线,垂足为E、F.
(1)求AB与CD的长;
(2)当矩形PECF的面积最大时,求点P运动的时间t;
(3)以点C为圆心,r为半径画圆,若圆C与斜边AB有且只有一个公共点时,求r的取值范围.
( http: / / www.21cnjy.com )
∴
(2)∵△APE∽△ABC,
( http: / / www.21cnjy.com )
6.【江阴市青阳片】如图①,梯形ABC ( http: / / www.21cnjy.com )D中,∠C=90°.动点E、F同时从点B出发,点E沿折线 BA—AD—DC运动到点C时停止运动,点F沿BC运动到点C时停止运动,它们运动时的速度都是1 cm/s.设E、F出发t s时,△EBF的面积为y cm2.已知y与t的函数图象如图②所示,其中曲线OM为抛物线的一部分,MN、NP为线段.请根据图中的信息,解答下列问题:
(1)梯形上底的长AD=_____cm,梯形ABCD的面积_____cm2;
(2)当点E在BA、DC上运动时,分别求出y与t的函数关系式(注明自变量的取值范围);
(3)当t为何值时,△EBF与梯形ABCD的面积之比为1:2.
( http: / / www.21cnjy.com )试题解析:(1)2,14.
( http: / / www.21cnjy.com )7.【江阴市青阳片】小明遇到这样一个问题:如图1,在边长为啊a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积;
小明发现:分别延长QE,MF,NG,P ( http: / / www.21cnjy.com )H,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
( http: / / www.21cnjy.com )
请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积;
参考小明思考问题的方法,解决问题:
(3)如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则AD的长为__________.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )8.【靖江市】如图所示,在梯形ABCD中,AD∥BC,∠BDC=90°,E为DC上一点,∠BDE=∠DBC.
(1)求证: DE=CE;
(2)若 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 \* MERGEFORMAT ,试判断四边形ABED的形状,并说明理由.
( http: / / www.21cnjy.com )∵ HYPERLINK "http://www.21cnjy.com" ,∴AD=BE.
( http: / / www.21cnjy.com )
9.【靖江市】在平面直角坐标系xOy中,二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象过A(-1,-2)、 B(1,0)两点.
(1)求此二次函数的解析式并画出二次函数图象;
(2)点P(t,0)是x轴上的一个 ( http: / / www.21cnjy.com )动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
( http: / / www.21cnjy.com )作图如下:
( http: / / www.21cnjy.com )
10.【靖江市】已知⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为( HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 \* MERGEFORMAT ,0), HYPERLINK "http://www.21cnjy.com" EMBED Equation.3 CAB=90°, AC=AB,顶点A在⊙O上运动.
(1)设点A的横坐标为x,△ABC的面积 ( http: / / www.21cnjy.com )为S,求S与x之间的函数关系式,并求出S的最大值与最小值;(2)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.
( http: / / www.21cnjy.com )AB的长,进而求出面积的表达式,结合定义域,根据一次函数的性质确定最大最小值;
( http: / / www.21cnjy.com )②当点A位于第四象限时(如图2),点A的坐标为(,),
( http: / / www.21cnjy.com )12.【靖江市】如图,抛物线过x轴上两点A(9,0) , C(-3,0), 且与y轴交于点B(0,-12).
(1)求抛物线的解析式;
(2)若动点P从点A出发,以每秒2个 ( http: / / www.21cnjy.com )单位沿射线AC方向运动;同时,点Q从点B出发,以每秒1个单位沿射线BA方向运动,当点P到达点C处时,两点同时停止运动.问当t为何值时,△APQ∽△AOB?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBNA面积的最大值.
( http: / / www.21cnjy.com )又∵AC=12,∴0≤t≤6.
∵△APQ∽△AOB,∴ HYPERLINK "http://www.21cnjy.com" ,即 HYPERLINK "http://www.21cnjy.com" ,解得 HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )13.【南京市高淳区】如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t s,四边形APQC的面积为y cm2.
(1)当t为何值时,△PBQ是直角三角形
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为x cm,试求y与x的函数关系式.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )(2)①过P作PH⊥BC,在Rt△PHB中,BP=4-t ,PH= HYPERLINK "http://www.21cnjy.com" ,
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
14.【无锡市塔影中学】一家图文广告公 ( http: / / www.21cnjy.com )司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
画板的边长(dm) 10 20
出售价(元/张) 160 220
(1)求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
15.【无锡市塔影中学】如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
(1)如图2,⊙O与Rt△AB ( http: / / www.21cnjy.com )C的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的 ( http: / / www.21cnjy.com )动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )∴y=;
③如图4,
( http: / / www.21cnjy.com )
16.【无锡市塔影中学】在平面直角坐标系中 ( http: / / www.21cnjy.com ),O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
( http: / / www.21cnjy.com )确定出解析式;
( http: / / www.21cnjy.com )∴OB=AB,BC=BD,
( http: / / www.21cnjy.com ) HYPERLINK "http://www.21cnjy.com"
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
17.【无锡市惠山北片】翻转 ( http: / / www.21cnjy.com )类的计算问题在全国各地的中考试卷中出现的频率很大,因此初三(5)班聪慧的小菲同学结合2011年苏州市数学中考卷的倒数第二题对这类问题进行了专门的研究。你能和小菲一起解决下列各问题吗?(以下各问只要求写出必要的计算过程和简洁的文字说明即可。)
(1)如图①,小菲同学把一个边长为1的 ( http: / / www.21cnjy.com )正三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片向右翻转一周回到初始位置,求顶点O所经过的路程;并求顶点O所经过的路线;
(2)小菲进行类比研究:如图②,她把边 ( http: / / www.21cnjy.com )长为1的正方形纸片OABC放在直线l2上,OA边与直线l2重合,然后将正方形纸片向右翻转若干次.她提出了如下问题:
问题①:若正方形纸片OABC接上述方法翻转一周回到初始位置,求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 。
(3)①小菲又进行了进一步的拓展研究,若 ( http: / / www.21cnjy.com )把这个正三角形的一边OA与这个正方形的一边OA重合(如图3),然后让这个正三角形在正方形上翻转,直到正三角形第一次回到初始位置(即OAB的相对位置和初始时一样),求顶点O所经过的总路程。
②若把边长为1的正方形OABC放在边 ( http: / / www.21cnjy.com )长为1的正五边形OABCD上翻转(如图④),直到正方形第一次回到初始位置,求顶点O所经过的总路程。
(4)规律总结,边长相等的两个正多边 ( http: / / www.21cnjy.com )形,其中一个在另一个上翻转,当翻转后第一次回到初始位置时,该正多边形翻转的次数一定是两正多边形边数的___________。
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )18.【无锡市惠山北片】如图,二次函数的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
(1)请直接写出点D的坐标:
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
( http: / / www.21cnjy.com )试题解析:(1)(﹣3,4);
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
19.【扬州市邗江区】如图①,已知线段 ( http: / / www.21cnjy.com )AB=8,以AB为直径作半圆O,再以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D。
(1)判断线段AP与PD的大小关系,并说明理由;
(2)连接PC,当∠ACP=600时,求弧AD的长;
(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.
( http: / / www.21cnjy.com )又∵OA=OD,∴AP=PD.
( http: / / www.21cnjy.com )
连接OP,同①可得,△APO∽△AED.∴ HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )际问题列函数关系式;8.相似三角形的判定和性质;9.分类思想的应用.
20.【扬州市邗江区】如图,抛物线 HYPERLINK "http://www.21cnjy.com" 与x轴交于点A(—2,0),交y轴于点B(0, HYPERLINK "http://www.21cnjy.com" ).直 HYPERLINK "http://www.21cnjy.com" 过点A与y轴交于点C,与抛物线的另一个交点是D.
(1)求抛物线 HYPERLINK "http://www.21cnjy.com" 与直线 HYPERLINK "http://www.21cnjy.com" 的解析式;
(2)设点P是直线AD下方的抛物线上一动 ( http: / / www.21cnjy.com )点(不与点A、D重合),过点P作 y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m与x的函数关系式,并求出m的最大值.
( http: / / www.21cnjy.com )试题解析:(1)∵ HYPERLINK "http://www.21cnjy.com" 经过点A(—2,0)和B(0, HYPERLINK "http://www.21cnjy.com" )
( http: / / www.21cnjy.com )
当x=2时,y=—3; 当x=4时,y= HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )∴ HYPERLINK "http://www.21cnjy.com" ,即 HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )21.【泰州市姜堰区】正常水位时,抛物线拱桥下的水面宽为BC=20m,水面上升3m达到该地警戒水位DE时,桥下水面宽为10m. 若以BC所在直线为x轴,BC的垂直平分线为y轴,建立如图所示的平面直角坐标系.
(1)求桥孔抛物线的函数关系式;
(2)如果水位以0.2m/h的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没;
(3)当达到警戒水位时,一艘装有防汛器材的船,露出水面部分的宽为4m,高为0.75m,通过计算说明该船能否顺利通过此拱桥?
( http: / / www.21cnjy.com )22.【泰州市姜堰区】如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P,Q分别从O、B两点同时出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,设动点P、Q运动时间为t(单位:s)
(1)当t为何值时,四边形PABQ是平行四边形,请写出推理过程;
(2)通过推理论证:在P、Q的运动过程中,线段DE的长度不变;
( http: / / www.21cnjy.com )23.【泰州市姜堰区】如图,在⊙O中,AB为⊙O的直径,AC为弦,OC=4,∠OAC=60°.
(1)求∠AOC的度数;
(2)在图(1)中,P为直径BA的延长线上一点,且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,求证:PC为⊙O的切线.
(3)如图(2),一动点M从A点出发,在⊙O上按逆时针方向运动一周(点M不与点C重合),当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,求动点M所经过的弧长.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为 HYPERLINK "http://www.21cnjy.com" .
( http: / / www.21cnjy.com )24.【泰州市姜堰区】已知,关于x的二次函数, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (k为正整数).
(1)若二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象与x轴有两个交点,求k的值.
(2)若关于x的一元二次方程 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.
(3)将(2)中的抛物线平移,当顶 ( http: / / www.21cnjy.com )点至原点时,直线y=2x+b交抛物线于A(-1,n)、B(2,t)两点,问在y轴上是否存在一点C,使得△ABC的内心在y轴上.若存在,求出点C的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )即为所求C点,坐标为(0,-4).
考点: 1. 二次函数的图象与x轴交点问题;2. 一元二次方程根的判别式;3. 二次函数与不等式组;4.轴对称的应用.
25.【无锡市前洲中学】如图,一条抛 ( http: / / www.21cnjy.com )物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,OA=5,AB=2.点E在线段OC上,作∠MEN=∠AOC,使∠MEN的一边始终经过点A,另一边交线段BC于点F,连接AF.
(1)求抛物线的解析式;
(2)当点F是BC的中点时,求点E的坐标;
(3)当△AEF是等腰三角形时,求点E的坐标.
( http: / / www.21cnjy.com )从而点E的坐标为(,0)
(3)由(2)中相似还可知AO:EC=AE:EF,若△AEF为等腰三角形,则有三种可能.
( http: / / www.21cnjy.com )
26.【无锡市前洲中学】如图①,正方形 ( http: / / www.21cnjy.com )ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A B C D匀速运动,同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,设运动的时间为t秒.
(1)当P点在边AB上运动时 ( http: / / www.21cnjy.com ),点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)如果点P、Q保持原速 ( http: / / www.21cnjy.com )度不变,当点P沿A B C D匀速运动时,OP与PQ能否相等?若能,求出所有符合条件的t的值;若不能,请说明理由.
( http: / / www.21cnjy.com )设△OPQ的面积为S,计算可得答案.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
E
同课章节目录
