2022—2023学年北师大版数学七年级下册2.2.2利用内错角、同旁内角判定两条直线平行课件(共20张PPT)
文档属性
| 名称 | 2022—2023学年北师大版数学七年级下册2.2.2利用内错角、同旁内角判定两条直线平行课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 251.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
2.2 探索直线平行的条件
第二章 相交线与平行线
第2课时 利用内错角、同旁内角判定两条直线平行
教学目标:
1,进一步理解内错角、同旁内角的意义及对直线平行判定的作用。
(重点)
2,几何证明题的逻辑推理、应用是本节学习的难点。
自主学习1:
自主学习p47的内容,回答下列问题:
1,内错角的概念是什么?怎么用几何图形表示?
2,同旁内角的概念是什么?怎么用几何图形表示?
A
C
B
D
E
F
1
2
3
4
5
6
7
8
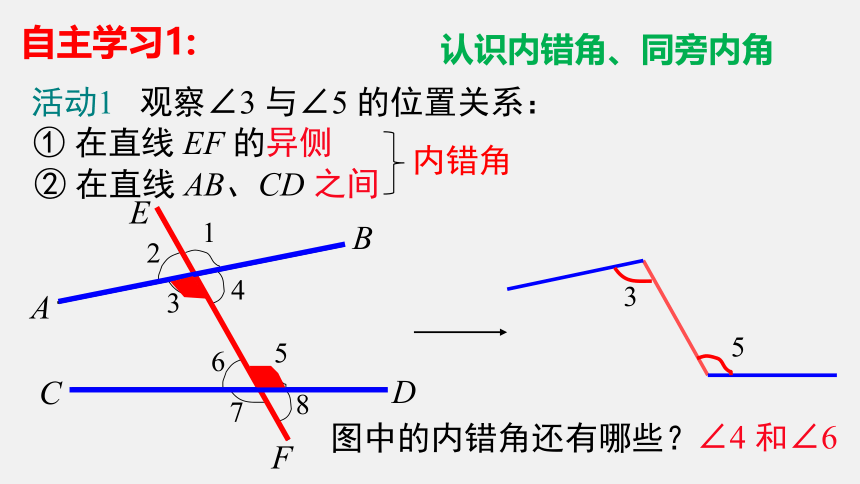
活动1 观察∠3 与∠5 的位置关系:
① 在直线 EF 的异侧
② 在直线 AB、CD 之间
3
5
∠4 和∠6
图中的内错角还有哪些?
内错角
认识内错角、同旁内角
自主学习1:
A
C
B
D
E
F
1
2
3
4
5
6
7
8
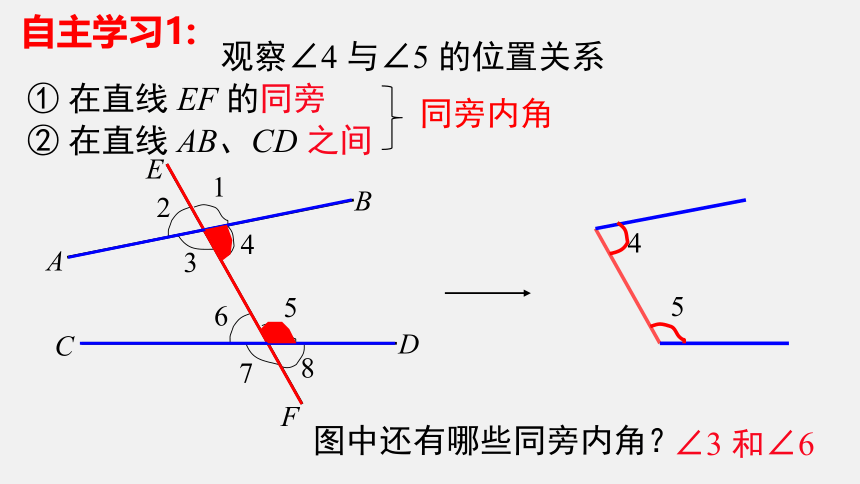
观察∠4 与∠5 的位置关系
① 在直线 EF 的同旁
② 在直线 AB、CD 之间
4
5
图中还有哪些同旁内角?
同旁内角
∠3 和∠6
自主学习1:
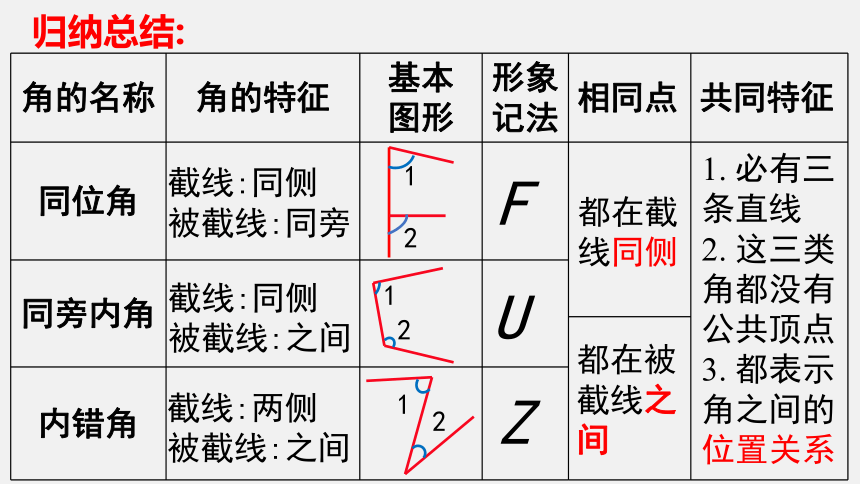
角的名称 角的特征 基本 图形 形象记法 相同点 共同特征
同位角
同旁内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
1. 必有三条直线
2. 这三类角都没有公共顶点
3. 都表示角之间的位置关系
归纳总结:
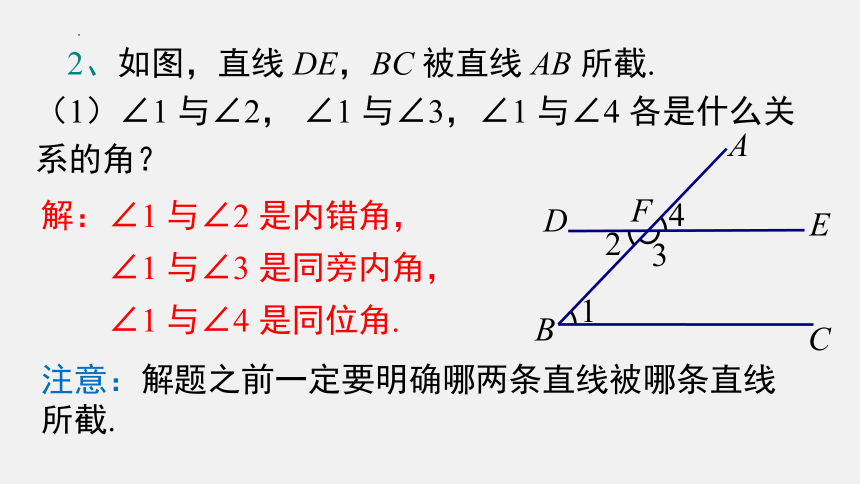
1、如图,直线 DE 截 AB,AC,构成 8 个角,指出其中所有的同位角,内错角,同旁内角.
解:两条直线 AB,AC 被直线 DE 所截,所以 8 个角中,同位角有:∠1 与∠8,∠2 与∠5,∠3 与∠6,∠4 与∠7;内错角有:∠1 与∠6,∠4 与∠5;同旁内角有:∠1 与∠5,∠4 与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
自主练习:
2、如图,直线 DE,BC 被直线 AB 所截.
(1)∠1 与∠2, ∠1 与∠3,∠1 与∠4 各是什么关系的角?
4
3
2
1
F
E
D
C
B
A
解:∠1 与∠2 是内错角,
∠1 与∠3 是同旁内角,
∠1 与∠4 是同位角.
注意:解题之前一定要明确哪两条直线被哪条直线所截.
解:如果∠1 =∠4,由对顶角相等,得∠2 =∠4,
那么∠1 =∠2.
因为∠3 和∠4 互补,即∠4 +∠3 =180°,
又∠1 =∠4,
所以∠1 +∠3 = 180°,
即∠1 与∠3 互补.
(2)如果∠1 =∠4,那么∠1 与∠2 相等吗?∠1 与∠3
互补吗?为什么?
4
3
2
1
F
E
D
C
B
A
问题1 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 3 = 2,能推得 a∥b 吗?试一试.
解:∵ 1 = 3(对顶角相等),
3 = 2(已知),
∴ 1 = 2.
∴ a∥b(同位角相等,两直线平行).
2
b
a
1
3
讨论并完成
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠1 =∠2 (已知),
∴ a∥b (内错角相等,两直线平行).
应用格式:
2
b
a
1
归纳总结:
问题2 如图,如果 1 + 2 = 180°,能判定 a∥b 吗
解:能. 理由如下:
∵ 1 + 2 = 180° (已知),
1 + 3 = 180° (邻补角的性质),
∴ 2 = 3 (同角的补角相等).
∴ a∥b (同位角相等,两直线平行).
c
2
b
a
1
3
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
∵∠1 +∠2 = 180° (已知),
∴ a∥b (同旁内角互补,两直线平行).
归纳总结:
1. 如图,可以确定 AB∥CE 的条件是 ( )
A. ∠2 =∠B
B. ∠1 =∠A
C. ∠3 =∠B
D. ∠3 =∠A
C
1
2
3
A
E
B
C
D
自主练习:
2. 如图,已知∠1 = 30°,若∠2 或∠3 满足条件
____________________,则 a∥b.
2
1
3
a
b
c
∠2 = 150° 或∠3 = 30°
3. 如图.(1)从∠1 = ∠4,可以推出 ∥ ,
理由是 .
(2) 从∠ABC +∠ = 180°,可以推出 AB∥CD,理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
(3) 从∠ =∠2,可以推出 AD∥BC,
理由是 .
(4) 从∠5 =∠ ,可以推出 AB∥CD,
理由是 .
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
理由如下:
∵ AC 平分∠DAB(已知),
∴ ∠1 =∠2 (角平分线定义).
又∵ ∠1 = ∠3(已知),
∴ ∠2 =∠3(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
4. 如图,已知∠1 =∠3,AC 平分∠DAB,你能判定
哪两条直线平行?请说明理由.
2
3
A
B
C
D
)
)
1
(
解:AB∥CD.
1. 同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
2. 在图形中判断三线八角的方法 (描图法):
① 把两个角在图中描画出来;
② 找到两个角的公共直线;
③ 观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式(旋转、对称形状)也是符合的.
归纳总结:
判定两条直线平行的方法
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴ a∥b.
_______相等, 两直线平行 ∵ (已知), ∴ a∥b.
________互补, 两直线平行 ∵ (已知), ∴ a∥b.
a
b
c
1
2
4
3
∠1 =∠2
∠3 =∠2
∠2 +∠4 = 180°
同位角
内错角
同旁内角
归纳总结:
2.2 探索直线平行的条件
第二章 相交线与平行线
第2课时 利用内错角、同旁内角判定两条直线平行
教学目标:
1,进一步理解内错角、同旁内角的意义及对直线平行判定的作用。
(重点)
2,几何证明题的逻辑推理、应用是本节学习的难点。
自主学习1:
自主学习p47的内容,回答下列问题:
1,内错角的概念是什么?怎么用几何图形表示?
2,同旁内角的概念是什么?怎么用几何图形表示?
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动1 观察∠3 与∠5 的位置关系:
① 在直线 EF 的异侧
② 在直线 AB、CD 之间
3
5
∠4 和∠6
图中的内错角还有哪些?
内错角
认识内错角、同旁内角
自主学习1:
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察∠4 与∠5 的位置关系
① 在直线 EF 的同旁
② 在直线 AB、CD 之间
4
5
图中还有哪些同旁内角?
同旁内角
∠3 和∠6
自主学习1:
角的名称 角的特征 基本 图形 形象记法 相同点 共同特征
同位角
同旁内角
内错角
F
Z
U
截线:同侧
被截线:同旁
截线:同侧
被截线:之间
截线:两侧
被截线:之间
1
2
1
2
1
2
都在截线同侧
都在被截线之间
1. 必有三条直线
2. 这三类角都没有公共顶点
3. 都表示角之间的位置关系
归纳总结:
1、如图,直线 DE 截 AB,AC,构成 8 个角,指出其中所有的同位角,内错角,同旁内角.
解:两条直线 AB,AC 被直线 DE 所截,所以 8 个角中,同位角有:∠1 与∠8,∠2 与∠5,∠3 与∠6,∠4 与∠7;内错角有:∠1 与∠6,∠4 与∠5;同旁内角有:∠1 与∠5,∠4 与∠6.
E
D
C
B
A
8
7
6
5
4
3
2
1
自主练习:
2、如图,直线 DE,BC 被直线 AB 所截.
(1)∠1 与∠2, ∠1 与∠3,∠1 与∠4 各是什么关系的角?
4
3
2
1
F
E
D
C
B
A
解:∠1 与∠2 是内错角,
∠1 与∠3 是同旁内角,
∠1 与∠4 是同位角.
注意:解题之前一定要明确哪两条直线被哪条直线所截.
解:如果∠1 =∠4,由对顶角相等,得∠2 =∠4,
那么∠1 =∠2.
因为∠3 和∠4 互补,即∠4 +∠3 =180°,
又∠1 =∠4,
所以∠1 +∠3 = 180°,
即∠1 与∠3 互补.
(2)如果∠1 =∠4,那么∠1 与∠2 相等吗?∠1 与∠3
互补吗?为什么?
4
3
2
1
F
E
D
C
B
A
问题1 两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
如图,由 3 = 2,能推得 a∥b 吗?试一试.
解:∵ 1 = 3(对顶角相等),
3 = 2(已知),
∴ 1 = 2.
∴ a∥b(同位角相等,两直线平行).
2
b
a
1
3
讨论并完成
判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠1 =∠2 (已知),
∴ a∥b (内错角相等,两直线平行).
应用格式:
2
b
a
1
归纳总结:
问题2 如图,如果 1 + 2 = 180°,能判定 a∥b 吗
解:能. 理由如下:
∵ 1 + 2 = 180° (已知),
1 + 3 = 180° (邻补角的性质),
∴ 2 = 3 (同角的补角相等).
∴ a∥b (同位角相等,两直线平行).
c
2
b
a
1
3
判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
应用格式:
2
b
a
1
∵∠1 +∠2 = 180° (已知),
∴ a∥b (同旁内角互补,两直线平行).
归纳总结:
1. 如图,可以确定 AB∥CE 的条件是 ( )
A. ∠2 =∠B
B. ∠1 =∠A
C. ∠3 =∠B
D. ∠3 =∠A
C
1
2
3
A
E
B
C
D
自主练习:
2. 如图,已知∠1 = 30°,若∠2 或∠3 满足条件
____________________,则 a∥b.
2
1
3
a
b
c
∠2 = 150° 或∠3 = 30°
3. 如图.(1)从∠1 = ∠4,可以推出 ∥ ,
理由是 .
(2) 从∠ABC +∠ = 180°,可以推出 AB∥CD,理由是 .
A
B
C
D
1
2
3
4
5
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
(3) 从∠ =∠2,可以推出 AD∥BC,
理由是 .
(4) 从∠5 =∠ ,可以推出 AB∥CD,
理由是 .
3
内错角相等,两直线平行
ABC
同位角相等,两直线平行
A
B
C
D
1
2
3
4
5
理由如下:
∵ AC 平分∠DAB(已知),
∴ ∠1 =∠2 (角平分线定义).
又∵ ∠1 = ∠3(已知),
∴ ∠2 =∠3(等量代换).
∴ AB∥CD(内错角相等,两直线平行).
4. 如图,已知∠1 =∠3,AC 平分∠DAB,你能判定
哪两条直线平行?请说明理由.
2
3
A
B
C
D
)
)
1
(
解:AB∥CD.
1. 同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
2. 在图形中判断三线八角的方法 (描图法):
① 把两个角在图中描画出来;
② 找到两个角的公共直线;
③ 观察所描的角,判断所属“字母”类型,同位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式(旋转、对称形状)也是符合的.
归纳总结:
判定两条直线平行的方法
文字叙述 符号语言 图形
相等, 两直线平行 ∵ (已知), ∴ a∥b.
_______相等, 两直线平行 ∵ (已知), ∴ a∥b.
________互补, 两直线平行 ∵ (已知), ∴ a∥b.
a
b
c
1
2
4
3
∠1 =∠2
∠3 =∠2
∠2 +∠4 = 180°
同位角
内错角
同旁内角
归纳总结:
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
