-2013-2014学年高一下学期第一次检测数学试题
文档属性
| 名称 | -2013-2014学年高一下学期第一次检测数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 78.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-17 09:25:39 | ||
图片预览

文档简介
高一下学期第一次检测数学试题
填空题
函数+2最小正周期为____________
空间两点的距离为,则
求过两点且圆心在直线上的圆的标准方程________
已知圆与轴相切,则实数
已知角的终边经过点,则
函数的图象向右平移个单位后,再纵坐标不变,横坐标变为原来的2倍,所得图象的函数解析式为_____
函数的单调减区间为______________
函数的值域___________________
化简
已知直线与圆的交点关于直线对称,则
设集合,当,则的最小值为_________
定义在区间上的函数的图象与的图像的交点为,过点作轴于点,直线与的图象交于点,则线段的长为___
1
在平面直角坐标系中,已知圆C:
,直线经过点若对任意的实数,直线被圆C截得的弦长都是定值,则直线的方程为_________
解答题
(本题满分14分)
1.已知,
求的值 (2)求的值
2.证明:
(本题满分14分):
已知直线与圆C:相交于两点,弦的中点为。(1)实数的取值范围以及直线方程
若弦,求圆的方程
2
17.(本题满分15分)
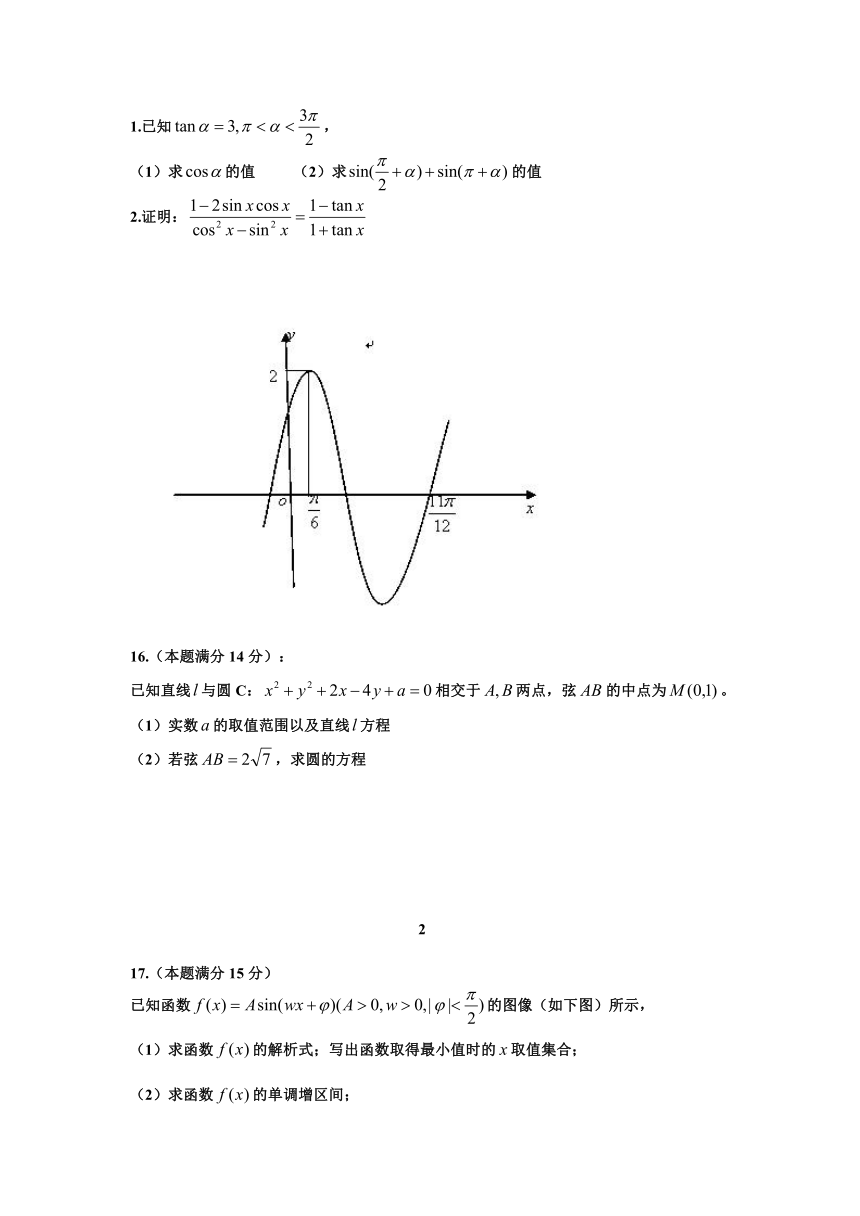
已知函数的图像(如下图)所示,
求函数的解析式;写出函数取得最小值时的取值集合;
求函数的单调增区间;
若在上恒成立,求的取值范围
(本题满分15分)
用一根长为10的绳索围成一个圆心角为,半径不超过2的扇形场地,设扇形的半径为,面积为。
写出关于的表达式,并求出此函数的定义域
当半径和圆心角分别是多少时,所围成的扇形场地的面积最大,并求最大面积
3
(本题满分16分)
已知半径为的圆的圆心在上,圆心的横坐标是整数,且与直线相切
求圆的方程
设直线与圆相交于两点,求实数的取范围
在(2)的条件下,是否存在实数,使得弦的垂直平分线过点,若存在,求出实数的值;若不存在,说明理由。
20.(本题满分16分):平面直角坐标系中,直线截以原点O为圆心的圆所得的弦长为
(1)求圆O的方程;
(2)若直线与圆O切于第一象限,且与轴分别交于D,E,当DE长最小时,求直 线的方程;
(3)设M,P是圆O上任意两点,点M关于轴的对称点为N,若直线MP、NP分别交于轴于点(m,0)和(n,0),问这两点的横坐标之积mn是否为定值?若是,请求出该定值;若不是,请说明理由。
4
填空题
函数+2最小正周期为____________
空间两点的距离为,则
求过两点且圆心在直线上的圆的标准方程________
已知圆与轴相切,则实数
已知角的终边经过点,则
函数的图象向右平移个单位后,再纵坐标不变,横坐标变为原来的2倍,所得图象的函数解析式为_____
函数的单调减区间为______________
函数的值域___________________
化简
已知直线与圆的交点关于直线对称,则
设集合,当,则的最小值为_________
定义在区间上的函数的图象与的图像的交点为,过点作轴于点,直线与的图象交于点,则线段的长为___
1
在平面直角坐标系中,已知圆C:
,直线经过点若对任意的实数,直线被圆C截得的弦长都是定值,则直线的方程为_________
解答题
(本题满分14分)
1.已知,
求的值 (2)求的值
2.证明:
(本题满分14分):
已知直线与圆C:相交于两点,弦的中点为。(1)实数的取值范围以及直线方程
若弦,求圆的方程
2
17.(本题满分15分)
已知函数的图像(如下图)所示,
求函数的解析式;写出函数取得最小值时的取值集合;
求函数的单调增区间;
若在上恒成立,求的取值范围
(本题满分15分)
用一根长为10的绳索围成一个圆心角为,半径不超过2的扇形场地,设扇形的半径为,面积为。
写出关于的表达式,并求出此函数的定义域
当半径和圆心角分别是多少时,所围成的扇形场地的面积最大,并求最大面积
3
(本题满分16分)
已知半径为的圆的圆心在上,圆心的横坐标是整数,且与直线相切
求圆的方程
设直线与圆相交于两点,求实数的取范围
在(2)的条件下,是否存在实数,使得弦的垂直平分线过点,若存在,求出实数的值;若不存在,说明理由。
20.(本题满分16分):平面直角坐标系中,直线截以原点O为圆心的圆所得的弦长为
(1)求圆O的方程;
(2)若直线与圆O切于第一象限,且与轴分别交于D,E,当DE长最小时,求直 线的方程;
(3)设M,P是圆O上任意两点,点M关于轴的对称点为N,若直线MP、NP分别交于轴于点(m,0)和(n,0),问这两点的横坐标之积mn是否为定值?若是,请求出该定值;若不是,请说明理由。
4
同课章节目录
