《圆》(同步练习)五年级下册苏教版三年(有答案)
文档属性
| 名称 | 《圆》(同步练习)五年级下册苏教版三年(有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 161.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 11:51:16 | ||
图片预览




文档简介
苏教版数学五年级下册同步练习
《圆》
学校:___________姓名:___________班级:___________
一、选择题(16分)
1.某班50人参加考试,其中优秀21人,良好15人,及格10人,不及格4人,如果用扇形统计图把这个班的考试结果表示出来,那么及格人数的扇形圆心角是( )度。
A.100 B.72 C.30 D.20
2.用圆规画一个周长是18.84厘米的圆,圆规两脚的距离是( )厘米。
A.2 B.3 C.6 D.8
3.美术老师用彩色卡纸制作了一个2022年冬奥会吉祥物“冰墩墩”,制作时需要把一个直径4厘米的圆形纸片剪成两个半圆,这两个半圆的周长和是( )厘米。
A.10.28 B.12.56 C.16.56 D.20.56
4.如图,大圆01的半径是5厘米,小圆02的半径是2厘米。如小圆02围绕大圆01的圆周滚动一周,小圆O2的圆心移动了( )厘米。
A.14π B.21π C.24π D.49π
5.世界上第一个把圆周率的值精确到七位小数的数学家是( )。
A.刘徽 B.张衡 C.杨辉 D.祖冲之
6.下面说法错误的是( )。
A.两个质数相乘的积一定是合数
B.如果(a、b都是不为0的自然数),那么
C.大圆直径是小圆直径的3倍,则小圆面积是大圆面积的
D.如果,则
7.如图,长方形的长是a厘米,宽是b厘米,在长方形中剪掉一个直径为a厘米的半圆形,剩下阴影部分的周长是( )。
A.a+2b+πa÷2 B.(a+b)×2+πa÷2
C.a+b+πa÷2 D.
8.把一个直径为4厘米的圆32等分,然后拼成一个近似长方形,这个长方形的周长是( )厘米。
A.12.56 B.6.28 C.10.28 D.16.56
二、填空题(16分)
9.以一个圆的直径和半径的长分别为长和宽的长方形的面积是48cm,那么这个圆的面积是( )cm2。
10.圆的半径扩大到原来的3倍,周长扩大到原来的( )倍,面积扩大到原来的( )倍。
11.李伯伯要在一块长为10米、宽为6米的长方形地上建一个最大的圆形花园,需要给花园围上篱笆,所需篱笆的长度是( )米。
12.一只挂钟的时针长8厘米,分针长10厘米。从上午7时到晚上7时,分针“扫过”的面积为( )平方厘米,时针尖端“走过”( )厘米。
13.陈明用圆规和直尺画半圆,他将圆规两脚间的距离定为4厘米,画出的半圆的周长是( )厘米。
14.如下图,这个半圆的周长是( )厘米,做这个半圆至少需要长( )厘米,宽( )厘米的长方形。
15.用圆规画一个直径为10厘米的圆,圆规两脚间的距离应是( )厘米。如果把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长是( )厘米。
16.从一块长5分米、宽4分米的长方形木板上锯下一个最大的圆,剩下( )平方分米的木板没用。
三、判断题(10分)
17.如果一个圆的半径扩大到原来的3倍,那么它的周长扩大到原来的3倍,面积扩大到原来的9倍。( )
18.一个圆的周长是它半径的2π倍。( )
19.有甲、乙两个扇形,甲的圆心角比乙的大,所以甲的面积一定比乙的面积大。( )
20.圆有无数条对称轴,扇形只有1条对称轴。( )
21.在同一个圆内,扇形的圆心角越大,扇形的面积就越大。( )
四、图形计算(10分)
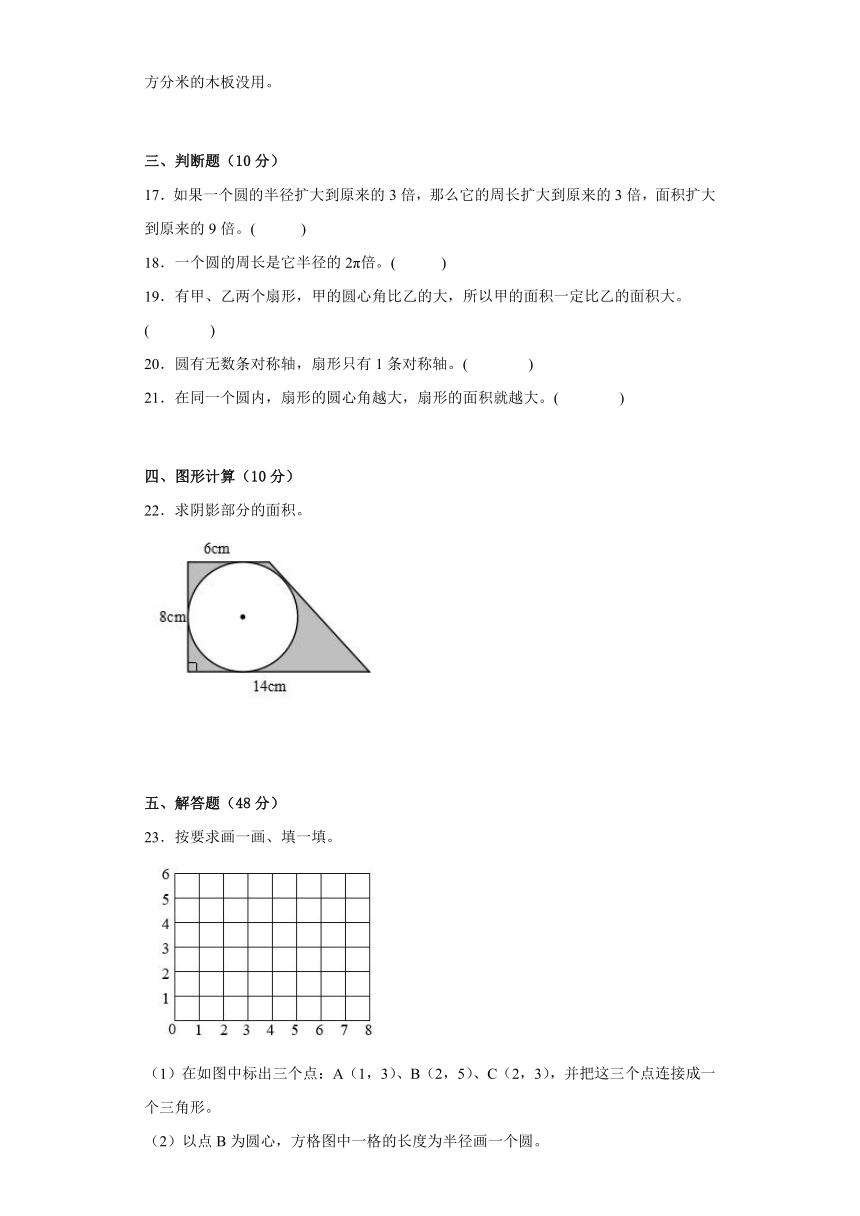
22.求阴影部分的面积。
五、解答题(48分)
23.按要求画一画、填一填。
(1)在如图中标出三个点:A(1,3)、B(2,5)、C(2,3),并把这三个点连接成一个三角形。
(2)以点B为圆心,方格图中一格的长度为半径画一个圆。
(3)将画出的整个图形绕C点顺时针旋转90度,画出旋转后的图形。
(4)如果要使点在(7,1)的位置,那整个图形要向( )平移( )格,再向( )平移( )格。
24.在下面一个边长为4厘米的正方形中画一个最大的圆。如果将这个圆剪去,剩下图形的面积是多少平方厘米?
25.刘老师骑自行车从家去学校用了12分钟,这辆自行车的车轮外直径大约是0.6米。按车轮每分钟转100圈计算,刘老师从家到学校大约有多少米?
26.下面的方格里有一个正方形,(每一个小方格的边长表示1厘米)
①先画图,再填空。
画图:在正方形里画一个最大的圆形。(辅助线用虚线,且保留痕迹)。
填空:这个圆的半径是( )厘米,圆心的位置用数对表示是( )。
②这个圆的周长与正方形的周长相比,相差( )厘米。(π取3.14)
27.学校的运动场如图:
(1)明明绕着这个运动场跑了2圈,一共跑了多少米?
(2)这个运动场的占地面积是多少平方米?
28.作图计算。下图正方形的面积是10平方厘米,请你以它的一个顶点为圆心,以它的边长为半径画一个圆,并标上圆心O,再求出这个圆的面积。
29.一个圆形花圃的周长是94.2米,学校准备把这个花圃的种牡丹花,这个圆形花圃种牡丹花的面积是多少平方米?
30.如图,阴影部分的面积是25平方米,求圆环面积。(π取3.14)
参考答案:
1.B
【分析】首先把这个班参加考试的总人数看作单位“1”,根据求一个数另一个数的百分之几,用除法求出及格的小数人数占全班小数人数的百分之几,再把周角的度数看成单位“1”,根据一个数乘百分数的意义,用乘法解答。
【详解】
及格人数的扇形圆心角是。
故答案为:
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,以及百分数意义的应用。
2.B
【分析】利用圆的周长公式,即C=2πr,得出r=C÷π÷2,求出圆的半径,因为圆规两脚之间的距离就是圆的半径,据此解答即可。
【详解】18.84÷3.14÷2=3(厘米)
故答案为:B
【点睛】此题主要考查圆的周长的计算方法的灵活应用。
3.D
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径,所以这两个半圆的周长和比圆的周长增加两条直径的长度,根据圆的周长公式:C=πd,把数据代入公式解答。
【详解】3.14×4+4×2
=12.56+8
=20.56(厘米)
故答案为:D
【点睛】此题考查的目的是理解半圆周长的意义,掌握半圆的公式及应用。
4.A
【分析】通过观察图形可知,小圆O2围绕大圆O1的圆周滚动一周,小圆O2的圆心移动的距离等于半径为(5+2)厘米的圆的周长,根据圆的周长公式:C=2πr,把数据代入公式解答。
【详解】π×(5+2)×2
=π×7×2
=14π(厘米)
故答案为:A
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
5.D
【分析】中国数学家祖冲之是世界上第一次把圆周率精确到小数点后第七位数字的人,比外国早了近一千年,他推算出圆周率的数值在3.1415926到3.1415927之间,也就是精确到小数点后第七位。
【详解】约l500年前,中国的数学家祖冲之是世界上第一个把圆周率的值精确到七位小数的人。
故答案为:D
【点睛】此题考查关于圆周率的历史,让学生记住祖冲之这位了不起的数学大师,增强民族自豪感。
6.B
【分析】合数是除了1和它本身以外,还有其他因数的数,所以两个质数相乘,积一定是合数;
分数大小比较:分子相同,分母大的数反而比较小,所以如果(a、b都是不为0的自然数),则a>b,那么;
假设小圆的半径是2,则直径是4,大圆直径是小圆直径的3倍,则大圆的直径是12,半径是6,根据圆的面积公式可得,小圆的面积为(π×2×2),大圆的面积是(π×6×6),求一个数是另一个数的几分之几,用除法计算,所以小圆面积是大圆面积的(π×2×2)÷(π×6×6)=;
根据等式的性质求解出中x的值,再把x的值代入4÷x中,看是否等于10即可。
【详解】A.由分析可知,两个质数相乘的积一定是合数,此说法正确;
B.由分析可知,如果(a、b都是不为0的自然数),那么,所以题干说法错误;
C.据此分析可知,大圆直径是小圆直径的3倍,则小圆面积是大圆面积的,此说法正确;
D.
解:
4÷0.4=10
所以如果,则,此说法正确。
故答案为:B
【点睛】本题主要考查了质数与合数的定义、分数比较大小的方法、圆的认识以及面积公式、求一个数占另一个数的几分之几以及解方程,比较基础,需要熟练掌握。
7.A
【分析】结合图形可知,剩下阴影部分的周长=长方形的两条宽+长方形的一条长+半圆的周长,结合圆的周长计算公式,代入相应数值进行化简即可。
【详解】
故答案为:A
【点睛】解答本题的关键是明确阴影部分周长是由哪些部分组成的。
8.D
【分析】近似长方形的两条长的和是圆的周长,近似长方形的两条宽是圆的两条半径。据此,先求出圆的周长,再利用加法求出近似长方形的周长即可。
【详解】3.14×4+4÷2×2
=12.56+4
=16.56(厘米)
所以,这个长方形的周长是16.56厘米。
故答案为:D
【点睛】本题考查了圆和长方形的周长,解题关键是熟记公式。
9.75.36
【分析】根据题意可知,一个圆的直径和半径的长分别为长和宽,长方形的长是宽的2倍,根据长方形面积公式:面积=长×宽,即面积=直径×半径;由此可知,半径2=长方形面积÷2,再根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】3.14×(48÷2)
=3.14×24
=75.36(cm3)
以一个圆的直径和半径的长分别为长和宽的长方形的面积是48cm,那么这个圆的面积是75.36cm2。
【点睛】解答本题的关键明确利用长方形面积求出圆的半径的平方的值。
10. 3 9
【分析】假设出原来圆的半径,根据圆的周长公式“”求出原来和现在圆的周长,根据圆的面积公式“”求出原来和现在圆的面积,最后用除法求出周长和面积扩大的倍数,据此解答。
【详解】假设原来圆的半径为r,现在圆的半径为3r。
原来圆的周长:
现在圆的周长:=
÷=3
原来圆的面积:
现在圆的面积:=
÷=9
所以,圆的半径扩大到原来的3倍,周长扩大到原来的3倍,面积扩大到原来的9倍。
【点睛】掌握圆的周长和面积计算公式是解答题目的关键。
11.18.84
【分析】根据题意可知,在这块长方形地上建一个最大的圆形花园,这个圆的直径等于长方形的宽,根据圆的周长公式:C=πd,把数据代入公式解答。
【详解】3.14×6=18.84(米)
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
12. 3768 50.24
【分析】从上午7时到晚上7时,分针转动12圈,根据圆的面积=πr2,求出转动一圈“扫过”的面积,乘12即可;时针尖端转动一圈,圆的周长=2πr,列式计算即可。
【详解】3.14×102×12
=3.14×100×12
=3768(平方厘米)
2×3.14×8=50.24(厘米)
【点睛】关键是掌握并灵活运用圆的周长和面积公式。
13.20.56
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径的长度,根据半圆的周长公式:C=πr+2r,把数据代入公式解答。
【详解】3.14×4+4×2
=12.56+8
=20.56(厘米)
【点睛】此题主要考查半圆周长公式的灵活运用,关键是熟记公式。
14. 51.4 20 10
【分析】看图,半圆的直径是20厘米,根据圆的周长公式求出对应圆的周长,再除以2,求出半圆的弧长。将半圆的弧长加上直径,求出半圆的周长;
做这个半圆至少需要的长方形,长和直径相等,宽和半径相等,据此填空。
【详解】20×3.14÷2+20
=31.4+20
=51.4(厘米)
20÷2=10(厘米)
所以,这个半圆的周长是51.4厘米,做这个半圆至少需要长20厘米,宽10厘米的长方形。
【点睛】本题考查了半圆的周长的计算,半圆的周长=半圆的弧长+圆的直径。
15. 5 41.4
【分析】圆规两脚间的距离就是圆的半径,根据半径=直径÷2,据此求出圆规两脚间的距离;把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长比圆的周长多两条半径的长度。据此填空即可。
【详解】10÷2=5(厘米)
3.14×10+10
=31.4+10
=41.4(厘米)
用圆规画一个直径为10厘米的圆,圆规两脚间的距离应是5厘米。如果把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长是41.4厘米。
【点睛】本题考查圆的周长,明确圆规两脚间的距离就是圆的半径是解题的关键。
16.7.44
【分析】以长方形的宽为直径的圆是长方形木板上面积最大的圆,利用“”表示出圆的面积,剩下木板的面积=长方形的面积-圆形的面积。
【详解】分析可知,最大圆的半径为4÷2=2分米。
5×4-3.14×22
=20-12.56
=7.44(平方分米)
【点睛】找出最大圆的半径并熟记圆的面积计算公式是解答题目的关键。
17.√
【分析】设圆的半径为r,则圆的周长为,面积为;如果半径扩大到原来的3倍,那么扩大后的半径为3r,则扩大后的周长为,面积为。据此即可解答。
【详解】如果一个圆的半径扩大到原来的3倍,那么它的周长扩大到原来的3倍,面积扩大到原来的9倍。
故答案为:√
【点睛】本题主要考查圆的周长公式与面积公式的灵活运用。
18.√
【分析】根据“圆的周长=2πr”可知:圆的周长÷r=2π;可知:圆的周长是它半径的2π倍;由此判断即可。
【详解】因为圆的周长=2πr
所以圆的周长÷r=2π,
即圆的周长是它半径的2π倍。
所以原题的说法正确。
故答案为:√
【点睛】解答此题应根据圆的半径、圆周率和圆的周长三者之间的关系。
19.×
【分析】扇形的面积的大小与扇形的圆心角的度数和半径的大小有关,据此解答。
【详解】有甲、乙两个扇形,甲的圆心角比乙的大,但是它们的半径未知,所以甲的面积、乙的面积无法比较。
故答案为:×
【点睛】在同一个圆中,扇形的圆心角越大,扇形的面积越大。
20.√
【分析】平面内,如果一个图形沿一条直线对折,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是这个图形的对称轴,由此即可确定圆和扇形的对称轴的条数。
【详解】由分析可知,圆有无数条对称轴,扇形只有一条对称轴。
故答案为:√。
【点睛】此题考查了对称轴的定义和如何确定对称轴的条数。
21.√
【分析】根据扇形面积=πr ,进行分析。
【详解】在同一个圆内,说明半径一样,扇形的圆心角越大,扇形的面积就越大,说法正确。
故答案为:√
【点睛】本题考查了扇形面积,扇形面积就是看这个扇形占同半径圆的几分之几。
22.29.76cm2
【分析】观察图形可知,阴影部分面积=上底是6cm,下底是14cm,高是8cm的梯形面积-半径是(8÷2)cm的圆的面积,根据梯形面积公式:面积=(上底+下底)×高÷2;圆的面积公式:面积=π×半径2;代入数据,即可解答。
【详解】(6+14)×8÷2-3.14×(8÷2)2
=20×8÷2-3.14×16
=160÷2-50.24
=80-50.24
=29.76(cm2)
23.(1)(2)(3)见详解
(4)右;5;下;4。
【分析】(1)根据数对表示位置的方法:第一个数字表列,第二个数字表示行;由此找出A、B、C的位置,画出三角形;
(2)以点B为圆心,以一格长为半径,即可画圆;
(3)根据旋转的特征,图形绕点C顺时针旋转90度,点C不动,其余各对应点(线段)均绕点C顺时针旋转90度,即可;
(4)根据平移的特征,把整个图形向右移动5个格,再向下移动4个格,即可得到移动后的图形。
【详解】(1)(2)(3)见下图:
(4)如果要使点在(7,1)的位置,那整个图形要向右平移5格,再向下平移4格。
【点睛】本题考查数对、画圆、旋转和平移,根据各自的特征,进行解答。
24.3.44平方厘米
【分析】根据题意,在一个正方形中画一个最大的圆,那么圆的直径等于这个正方形的边长;如果将这个圆剪去,剩下图形的面积=正方形的面积-圆的面积;根据正方形的面积公式S=a2,圆的面积公式S=πr2,代入数据计算即可。
【详解】如图:
正方形的面积:
4×4=16(平方厘米)
圆的面积:
3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
剩下图形的面积:
16-12.56=3.44(平方厘米)
答:剩下图形的面积是3.44平方厘米。
【点睛】明确正方形内最大圆的直径等于这个正方形的边长,然后利用正方形的面积、圆的面积公式列式计算。
25.2260.8米
【分析】根据圆的周长公式:C=πd,把数据代入公式求出自行车车轮的周长,用车轮的周长乘每分钟转的圈数求出每分钟行驶的速度,然后根据路程=速度×时间,列式解答即可。
【详解】3.14×0.6×100×12
=1.884×100×12
=188.4×12
=2260.8(米)
答:刘老师从家到学校大约有2260.8米。
【点睛】此题主要考查圆的周长公式的灵活运用,以及路程、速度、时间三者之间的关系及应用,关键是熟记公式。
26.①2,(3,3)
②3.44
【分析】①连接正方形的对角线,对角线的交点就是圆心,然后以正方形边长的一半为半径画圆即可;再根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此解答即可;
②根据圆的周长公式:C=πd,正方形的周长=边长×4,分别求出它们的周长,然后再相减即可。
【详解】①如图所示:
这个圆的半径是2厘米,圆心的位置用数对表示是(3,3)。
②3.14×4=12.56(厘米)
4×4=16(厘米)
16-12.56=3.44(厘米)
这个圆的周长与正方形的周长相比,相差3.44厘米
【点睛】本题考查圆和正方形的周长,熟记公式是解题的关键。
27.(1)816.8米;(2)9426平方米
【分析】(1)观察图形可知,运动场的周长由2条110米的长度和一个直径为69米的圆的周长组成,根据圆周长公式可得,运动场的周长=,据此解答即可;
(2)运动场的面积等于一个直径为60米圆的面积加上一个长为110米、宽为60米的长方形面积,即,据此解答。
【详解】(1)
=
=
=816.8(米)
答:一共跑了816.8米。
(2)
=
=9426(平方米)
答:这个运动场的占地面积是9426平方米。
【点睛】本题考查了圆的周长公式和面积公式的灵活应用,明确运动场是由一个长方形和两个相同的半圆组成是解题的关键。
28.31.4平方厘米
【分析】以正方形的一个顶点为圆心,以它的边长为半径画一个圆,据此作图即可;由题意可知,根据圆的面积公式:S=πr2,正方形的面积=边长×边长,也就是正方形的面积相当于圆的半径的平方,据此进行计算即可。
【详解】如图所示:
3.14×10=31.4(平方厘米)
答:这个圆的面积是31.4平方厘米。
【点睛】本题考查圆的面积,明确正方形的面积相当于圆的半径的平方是解题的关键。
29.235.5平方米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆形花圃的半径,再根据圆的面积公式:面积=π×半径2,代入数据,求出花圃的面积,再把花圃的面积平均分成3份,其中的一份就是种牡丹花的面积,用花圃的面积÷3,,即可解答。
【详解】94.2÷3.14÷2
=30÷2
=15(米)
3.14×152÷3
=3.14×225÷3
=706.5÷3
=235.5(平方米)
答:这个圆形花圃种牡丹花的面积是235.5平方米。
【点睛】熟练掌握圆的周长公式和面积公式是解答本题的关键,要熟记公式,灵活运用。
30.157平方米
【分析】设大圆的半径为R,小圆的半径为r,则圆环的面积=大圆的面积﹣小圆的面积,阴影部分的面积=大三角形的面积﹣小三角形的面积,即R×R×﹣r×r×=﹣,于是可以用两圆的半径表示出阴影部分的面积,进而可以求出圆环的面积.
【详解】解:设大圆的半径为R,小圆的半径为r,
阴影部分的面积:﹣=25,
于是可得R2﹣r2=50(平方米),
所以圆环的面积:π×(R2﹣r2),
=3.14×50,
=157(平方米);
答:圆环的面积是157平方米.
【点睛】解答此题的关键是:设出半径,利用阴影部分的面积求得圆环的面积.
《圆》
学校:___________姓名:___________班级:___________
一、选择题(16分)
1.某班50人参加考试,其中优秀21人,良好15人,及格10人,不及格4人,如果用扇形统计图把这个班的考试结果表示出来,那么及格人数的扇形圆心角是( )度。
A.100 B.72 C.30 D.20
2.用圆规画一个周长是18.84厘米的圆,圆规两脚的距离是( )厘米。
A.2 B.3 C.6 D.8
3.美术老师用彩色卡纸制作了一个2022年冬奥会吉祥物“冰墩墩”,制作时需要把一个直径4厘米的圆形纸片剪成两个半圆,这两个半圆的周长和是( )厘米。
A.10.28 B.12.56 C.16.56 D.20.56
4.如图,大圆01的半径是5厘米,小圆02的半径是2厘米。如小圆02围绕大圆01的圆周滚动一周,小圆O2的圆心移动了( )厘米。
A.14π B.21π C.24π D.49π
5.世界上第一个把圆周率的值精确到七位小数的数学家是( )。
A.刘徽 B.张衡 C.杨辉 D.祖冲之
6.下面说法错误的是( )。
A.两个质数相乘的积一定是合数
B.如果(a、b都是不为0的自然数),那么
C.大圆直径是小圆直径的3倍,则小圆面积是大圆面积的
D.如果,则
7.如图,长方形的长是a厘米,宽是b厘米,在长方形中剪掉一个直径为a厘米的半圆形,剩下阴影部分的周长是( )。
A.a+2b+πa÷2 B.(a+b)×2+πa÷2
C.a+b+πa÷2 D.
8.把一个直径为4厘米的圆32等分,然后拼成一个近似长方形,这个长方形的周长是( )厘米。
A.12.56 B.6.28 C.10.28 D.16.56
二、填空题(16分)
9.以一个圆的直径和半径的长分别为长和宽的长方形的面积是48cm,那么这个圆的面积是( )cm2。
10.圆的半径扩大到原来的3倍,周长扩大到原来的( )倍,面积扩大到原来的( )倍。
11.李伯伯要在一块长为10米、宽为6米的长方形地上建一个最大的圆形花园,需要给花园围上篱笆,所需篱笆的长度是( )米。
12.一只挂钟的时针长8厘米,分针长10厘米。从上午7时到晚上7时,分针“扫过”的面积为( )平方厘米,时针尖端“走过”( )厘米。
13.陈明用圆规和直尺画半圆,他将圆规两脚间的距离定为4厘米,画出的半圆的周长是( )厘米。
14.如下图,这个半圆的周长是( )厘米,做这个半圆至少需要长( )厘米,宽( )厘米的长方形。
15.用圆规画一个直径为10厘米的圆,圆规两脚间的距离应是( )厘米。如果把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长是( )厘米。
16.从一块长5分米、宽4分米的长方形木板上锯下一个最大的圆,剩下( )平方分米的木板没用。
三、判断题(10分)
17.如果一个圆的半径扩大到原来的3倍,那么它的周长扩大到原来的3倍,面积扩大到原来的9倍。( )
18.一个圆的周长是它半径的2π倍。( )
19.有甲、乙两个扇形,甲的圆心角比乙的大,所以甲的面积一定比乙的面积大。( )
20.圆有无数条对称轴,扇形只有1条对称轴。( )
21.在同一个圆内,扇形的圆心角越大,扇形的面积就越大。( )
四、图形计算(10分)
22.求阴影部分的面积。
五、解答题(48分)
23.按要求画一画、填一填。
(1)在如图中标出三个点:A(1,3)、B(2,5)、C(2,3),并把这三个点连接成一个三角形。
(2)以点B为圆心,方格图中一格的长度为半径画一个圆。
(3)将画出的整个图形绕C点顺时针旋转90度,画出旋转后的图形。
(4)如果要使点在(7,1)的位置,那整个图形要向( )平移( )格,再向( )平移( )格。
24.在下面一个边长为4厘米的正方形中画一个最大的圆。如果将这个圆剪去,剩下图形的面积是多少平方厘米?
25.刘老师骑自行车从家去学校用了12分钟,这辆自行车的车轮外直径大约是0.6米。按车轮每分钟转100圈计算,刘老师从家到学校大约有多少米?
26.下面的方格里有一个正方形,(每一个小方格的边长表示1厘米)
①先画图,再填空。
画图:在正方形里画一个最大的圆形。(辅助线用虚线,且保留痕迹)。
填空:这个圆的半径是( )厘米,圆心的位置用数对表示是( )。
②这个圆的周长与正方形的周长相比,相差( )厘米。(π取3.14)
27.学校的运动场如图:
(1)明明绕着这个运动场跑了2圈,一共跑了多少米?
(2)这个运动场的占地面积是多少平方米?
28.作图计算。下图正方形的面积是10平方厘米,请你以它的一个顶点为圆心,以它的边长为半径画一个圆,并标上圆心O,再求出这个圆的面积。
29.一个圆形花圃的周长是94.2米,学校准备把这个花圃的种牡丹花,这个圆形花圃种牡丹花的面积是多少平方米?
30.如图,阴影部分的面积是25平方米,求圆环面积。(π取3.14)
参考答案:
1.B
【分析】首先把这个班参加考试的总人数看作单位“1”,根据求一个数另一个数的百分之几,用除法求出及格的小数人数占全班小数人数的百分之几,再把周角的度数看成单位“1”,根据一个数乘百分数的意义,用乘法解答。
【详解】
及格人数的扇形圆心角是。
故答案为:
【点睛】此题考查的目的是理解掌握扇形统计图的特点及作用,以及百分数意义的应用。
2.B
【分析】利用圆的周长公式,即C=2πr,得出r=C÷π÷2,求出圆的半径,因为圆规两脚之间的距离就是圆的半径,据此解答即可。
【详解】18.84÷3.14÷2=3(厘米)
故答案为:B
【点睛】此题主要考查圆的周长的计算方法的灵活应用。
3.D
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径,所以这两个半圆的周长和比圆的周长增加两条直径的长度,根据圆的周长公式:C=πd,把数据代入公式解答。
【详解】3.14×4+4×2
=12.56+8
=20.56(厘米)
故答案为:D
【点睛】此题考查的目的是理解半圆周长的意义,掌握半圆的公式及应用。
4.A
【分析】通过观察图形可知,小圆O2围绕大圆O1的圆周滚动一周,小圆O2的圆心移动的距离等于半径为(5+2)厘米的圆的周长,根据圆的周长公式:C=2πr,把数据代入公式解答。
【详解】π×(5+2)×2
=π×7×2
=14π(厘米)
故答案为:A
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
5.D
【分析】中国数学家祖冲之是世界上第一次把圆周率精确到小数点后第七位数字的人,比外国早了近一千年,他推算出圆周率的数值在3.1415926到3.1415927之间,也就是精确到小数点后第七位。
【详解】约l500年前,中国的数学家祖冲之是世界上第一个把圆周率的值精确到七位小数的人。
故答案为:D
【点睛】此题考查关于圆周率的历史,让学生记住祖冲之这位了不起的数学大师,增强民族自豪感。
6.B
【分析】合数是除了1和它本身以外,还有其他因数的数,所以两个质数相乘,积一定是合数;
分数大小比较:分子相同,分母大的数反而比较小,所以如果(a、b都是不为0的自然数),则a>b,那么;
假设小圆的半径是2,则直径是4,大圆直径是小圆直径的3倍,则大圆的直径是12,半径是6,根据圆的面积公式可得,小圆的面积为(π×2×2),大圆的面积是(π×6×6),求一个数是另一个数的几分之几,用除法计算,所以小圆面积是大圆面积的(π×2×2)÷(π×6×6)=;
根据等式的性质求解出中x的值,再把x的值代入4÷x中,看是否等于10即可。
【详解】A.由分析可知,两个质数相乘的积一定是合数,此说法正确;
B.由分析可知,如果(a、b都是不为0的自然数),那么,所以题干说法错误;
C.据此分析可知,大圆直径是小圆直径的3倍,则小圆面积是大圆面积的,此说法正确;
D.
解:
4÷0.4=10
所以如果,则,此说法正确。
故答案为:B
【点睛】本题主要考查了质数与合数的定义、分数比较大小的方法、圆的认识以及面积公式、求一个数占另一个数的几分之几以及解方程,比较基础,需要熟练掌握。
7.A
【分析】结合图形可知,剩下阴影部分的周长=长方形的两条宽+长方形的一条长+半圆的周长,结合圆的周长计算公式,代入相应数值进行化简即可。
【详解】
故答案为:A
【点睛】解答本题的关键是明确阴影部分周长是由哪些部分组成的。
8.D
【分析】近似长方形的两条长的和是圆的周长,近似长方形的两条宽是圆的两条半径。据此,先求出圆的周长,再利用加法求出近似长方形的周长即可。
【详解】3.14×4+4÷2×2
=12.56+4
=16.56(厘米)
所以,这个长方形的周长是16.56厘米。
故答案为:D
【点睛】本题考查了圆和长方形的周长,解题关键是熟记公式。
9.75.36
【分析】根据题意可知,一个圆的直径和半径的长分别为长和宽,长方形的长是宽的2倍,根据长方形面积公式:面积=长×宽,即面积=直径×半径;由此可知,半径2=长方形面积÷2,再根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【详解】3.14×(48÷2)
=3.14×24
=75.36(cm3)
以一个圆的直径和半径的长分别为长和宽的长方形的面积是48cm,那么这个圆的面积是75.36cm2。
【点睛】解答本题的关键明确利用长方形面积求出圆的半径的平方的值。
10. 3 9
【分析】假设出原来圆的半径,根据圆的周长公式“”求出原来和现在圆的周长,根据圆的面积公式“”求出原来和现在圆的面积,最后用除法求出周长和面积扩大的倍数,据此解答。
【详解】假设原来圆的半径为r,现在圆的半径为3r。
原来圆的周长:
现在圆的周长:=
÷=3
原来圆的面积:
现在圆的面积:=
÷=9
所以,圆的半径扩大到原来的3倍,周长扩大到原来的3倍,面积扩大到原来的9倍。
【点睛】掌握圆的周长和面积计算公式是解答题目的关键。
11.18.84
【分析】根据题意可知,在这块长方形地上建一个最大的圆形花园,这个圆的直径等于长方形的宽,根据圆的周长公式:C=πd,把数据代入公式解答。
【详解】3.14×6=18.84(米)
【点睛】此题主要考查圆的周长公式的灵活运用,关键是熟记公式。
12. 3768 50.24
【分析】从上午7时到晚上7时,分针转动12圈,根据圆的面积=πr2,求出转动一圈“扫过”的面积,乘12即可;时针尖端转动一圈,圆的周长=2πr,列式计算即可。
【详解】3.14×102×12
=3.14×100×12
=3768(平方厘米)
2×3.14×8=50.24(厘米)
【点睛】关键是掌握并灵活运用圆的周长和面积公式。
13.20.56
【分析】根据半圆周长的意义,半圆的周长等于该圆周长的一半加上一条直径的长度,根据半圆的周长公式:C=πr+2r,把数据代入公式解答。
【详解】3.14×4+4×2
=12.56+8
=20.56(厘米)
【点睛】此题主要考查半圆周长公式的灵活运用,关键是熟记公式。
14. 51.4 20 10
【分析】看图,半圆的直径是20厘米,根据圆的周长公式求出对应圆的周长,再除以2,求出半圆的弧长。将半圆的弧长加上直径,求出半圆的周长;
做这个半圆至少需要的长方形,长和直径相等,宽和半径相等,据此填空。
【详解】20×3.14÷2+20
=31.4+20
=51.4(厘米)
20÷2=10(厘米)
所以,这个半圆的周长是51.4厘米,做这个半圆至少需要长20厘米,宽10厘米的长方形。
【点睛】本题考查了半圆的周长的计算,半圆的周长=半圆的弧长+圆的直径。
15. 5 41.4
【分析】圆规两脚间的距离就是圆的半径,根据半径=直径÷2,据此求出圆规两脚间的距离;把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长比圆的周长多两条半径的长度。据此填空即可。
【详解】10÷2=5(厘米)
3.14×10+10
=31.4+10
=41.4(厘米)
用圆规画一个直径为10厘米的圆,圆规两脚间的距离应是5厘米。如果把这个圆等分成若干份,拼成一个近似的长方形,长方形的周长是41.4厘米。
【点睛】本题考查圆的周长,明确圆规两脚间的距离就是圆的半径是解题的关键。
16.7.44
【分析】以长方形的宽为直径的圆是长方形木板上面积最大的圆,利用“”表示出圆的面积,剩下木板的面积=长方形的面积-圆形的面积。
【详解】分析可知,最大圆的半径为4÷2=2分米。
5×4-3.14×22
=20-12.56
=7.44(平方分米)
【点睛】找出最大圆的半径并熟记圆的面积计算公式是解答题目的关键。
17.√
【分析】设圆的半径为r,则圆的周长为,面积为;如果半径扩大到原来的3倍,那么扩大后的半径为3r,则扩大后的周长为,面积为。据此即可解答。
【详解】如果一个圆的半径扩大到原来的3倍,那么它的周长扩大到原来的3倍,面积扩大到原来的9倍。
故答案为:√
【点睛】本题主要考查圆的周长公式与面积公式的灵活运用。
18.√
【分析】根据“圆的周长=2πr”可知:圆的周长÷r=2π;可知:圆的周长是它半径的2π倍;由此判断即可。
【详解】因为圆的周长=2πr
所以圆的周长÷r=2π,
即圆的周长是它半径的2π倍。
所以原题的说法正确。
故答案为:√
【点睛】解答此题应根据圆的半径、圆周率和圆的周长三者之间的关系。
19.×
【分析】扇形的面积的大小与扇形的圆心角的度数和半径的大小有关,据此解答。
【详解】有甲、乙两个扇形,甲的圆心角比乙的大,但是它们的半径未知,所以甲的面积、乙的面积无法比较。
故答案为:×
【点睛】在同一个圆中,扇形的圆心角越大,扇形的面积越大。
20.√
【分析】平面内,如果一个图形沿一条直线对折,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是这个图形的对称轴,由此即可确定圆和扇形的对称轴的条数。
【详解】由分析可知,圆有无数条对称轴,扇形只有一条对称轴。
故答案为:√。
【点睛】此题考查了对称轴的定义和如何确定对称轴的条数。
21.√
【分析】根据扇形面积=πr ,进行分析。
【详解】在同一个圆内,说明半径一样,扇形的圆心角越大,扇形的面积就越大,说法正确。
故答案为:√
【点睛】本题考查了扇形面积,扇形面积就是看这个扇形占同半径圆的几分之几。
22.29.76cm2
【分析】观察图形可知,阴影部分面积=上底是6cm,下底是14cm,高是8cm的梯形面积-半径是(8÷2)cm的圆的面积,根据梯形面积公式:面积=(上底+下底)×高÷2;圆的面积公式:面积=π×半径2;代入数据,即可解答。
【详解】(6+14)×8÷2-3.14×(8÷2)2
=20×8÷2-3.14×16
=160÷2-50.24
=80-50.24
=29.76(cm2)
23.(1)(2)(3)见详解
(4)右;5;下;4。
【分析】(1)根据数对表示位置的方法:第一个数字表列,第二个数字表示行;由此找出A、B、C的位置,画出三角形;
(2)以点B为圆心,以一格长为半径,即可画圆;
(3)根据旋转的特征,图形绕点C顺时针旋转90度,点C不动,其余各对应点(线段)均绕点C顺时针旋转90度,即可;
(4)根据平移的特征,把整个图形向右移动5个格,再向下移动4个格,即可得到移动后的图形。
【详解】(1)(2)(3)见下图:
(4)如果要使点在(7,1)的位置,那整个图形要向右平移5格,再向下平移4格。
【点睛】本题考查数对、画圆、旋转和平移,根据各自的特征,进行解答。
24.3.44平方厘米
【分析】根据题意,在一个正方形中画一个最大的圆,那么圆的直径等于这个正方形的边长;如果将这个圆剪去,剩下图形的面积=正方形的面积-圆的面积;根据正方形的面积公式S=a2,圆的面积公式S=πr2,代入数据计算即可。
【详解】如图:
正方形的面积:
4×4=16(平方厘米)
圆的面积:
3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
剩下图形的面积:
16-12.56=3.44(平方厘米)
答:剩下图形的面积是3.44平方厘米。
【点睛】明确正方形内最大圆的直径等于这个正方形的边长,然后利用正方形的面积、圆的面积公式列式计算。
25.2260.8米
【分析】根据圆的周长公式:C=πd,把数据代入公式求出自行车车轮的周长,用车轮的周长乘每分钟转的圈数求出每分钟行驶的速度,然后根据路程=速度×时间,列式解答即可。
【详解】3.14×0.6×100×12
=1.884×100×12
=188.4×12
=2260.8(米)
答:刘老师从家到学校大约有2260.8米。
【点睛】此题主要考查圆的周长公式的灵活运用,以及路程、速度、时间三者之间的关系及应用,关键是熟记公式。
26.①2,(3,3)
②3.44
【分析】①连接正方形的对角线,对角线的交点就是圆心,然后以正方形边长的一半为半径画圆即可;再根据用数对表示位置的方法,第一个数字表示列,第二个数字表示行,据此解答即可;
②根据圆的周长公式:C=πd,正方形的周长=边长×4,分别求出它们的周长,然后再相减即可。
【详解】①如图所示:
这个圆的半径是2厘米,圆心的位置用数对表示是(3,3)。
②3.14×4=12.56(厘米)
4×4=16(厘米)
16-12.56=3.44(厘米)
这个圆的周长与正方形的周长相比,相差3.44厘米
【点睛】本题考查圆和正方形的周长,熟记公式是解题的关键。
27.(1)816.8米;(2)9426平方米
【分析】(1)观察图形可知,运动场的周长由2条110米的长度和一个直径为69米的圆的周长组成,根据圆周长公式可得,运动场的周长=,据此解答即可;
(2)运动场的面积等于一个直径为60米圆的面积加上一个长为110米、宽为60米的长方形面积,即,据此解答。
【详解】(1)
=
=
=816.8(米)
答:一共跑了816.8米。
(2)
=
=9426(平方米)
答:这个运动场的占地面积是9426平方米。
【点睛】本题考查了圆的周长公式和面积公式的灵活应用,明确运动场是由一个长方形和两个相同的半圆组成是解题的关键。
28.31.4平方厘米
【分析】以正方形的一个顶点为圆心,以它的边长为半径画一个圆,据此作图即可;由题意可知,根据圆的面积公式:S=πr2,正方形的面积=边长×边长,也就是正方形的面积相当于圆的半径的平方,据此进行计算即可。
【详解】如图所示:
3.14×10=31.4(平方厘米)
答:这个圆的面积是31.4平方厘米。
【点睛】本题考查圆的面积,明确正方形的面积相当于圆的半径的平方是解题的关键。
29.235.5平方米
【分析】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆形花圃的半径,再根据圆的面积公式:面积=π×半径2,代入数据,求出花圃的面积,再把花圃的面积平均分成3份,其中的一份就是种牡丹花的面积,用花圃的面积÷3,,即可解答。
【详解】94.2÷3.14÷2
=30÷2
=15(米)
3.14×152÷3
=3.14×225÷3
=706.5÷3
=235.5(平方米)
答:这个圆形花圃种牡丹花的面积是235.5平方米。
【点睛】熟练掌握圆的周长公式和面积公式是解答本题的关键,要熟记公式,灵活运用。
30.157平方米
【分析】设大圆的半径为R,小圆的半径为r,则圆环的面积=大圆的面积﹣小圆的面积,阴影部分的面积=大三角形的面积﹣小三角形的面积,即R×R×﹣r×r×=﹣,于是可以用两圆的半径表示出阴影部分的面积,进而可以求出圆环的面积.
【详解】解:设大圆的半径为R,小圆的半径为r,
阴影部分的面积:﹣=25,
于是可得R2﹣r2=50(平方米),
所以圆环的面积:π×(R2﹣r2),
=3.14×50,
=157(平方米);
答:圆环的面积是157平方米.
【点睛】解答此题的关键是:设出半径,利用阴影部分的面积求得圆环的面积.
