折线统计图(同步练习)-五年级下册数学苏教版(含答案)
文档属性
| 名称 | 折线统计图(同步练习)-五年级下册数学苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 550.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 13:34:38 | ||
图片预览




文档简介
苏教版数学五年级下册同步练习
《折线统计图》
学校:___________姓名:___________班级:___________
一、选择题(16分)
1.要反映2021年上半年凤凰小学每月用水量的变化情况,应选用( )。
A.折线统计图 B.条形统计图 C.复式统计表 D.无法确定
2.下面的信息资料中,最适合用折线统计图表示的是( )。
A.实验小学五年级各班学生人数 B.张小明6~12岁身高变化情况
C.学校图书室各类图书的数量 D.某品牌汽车2021年各种车型的销售数量
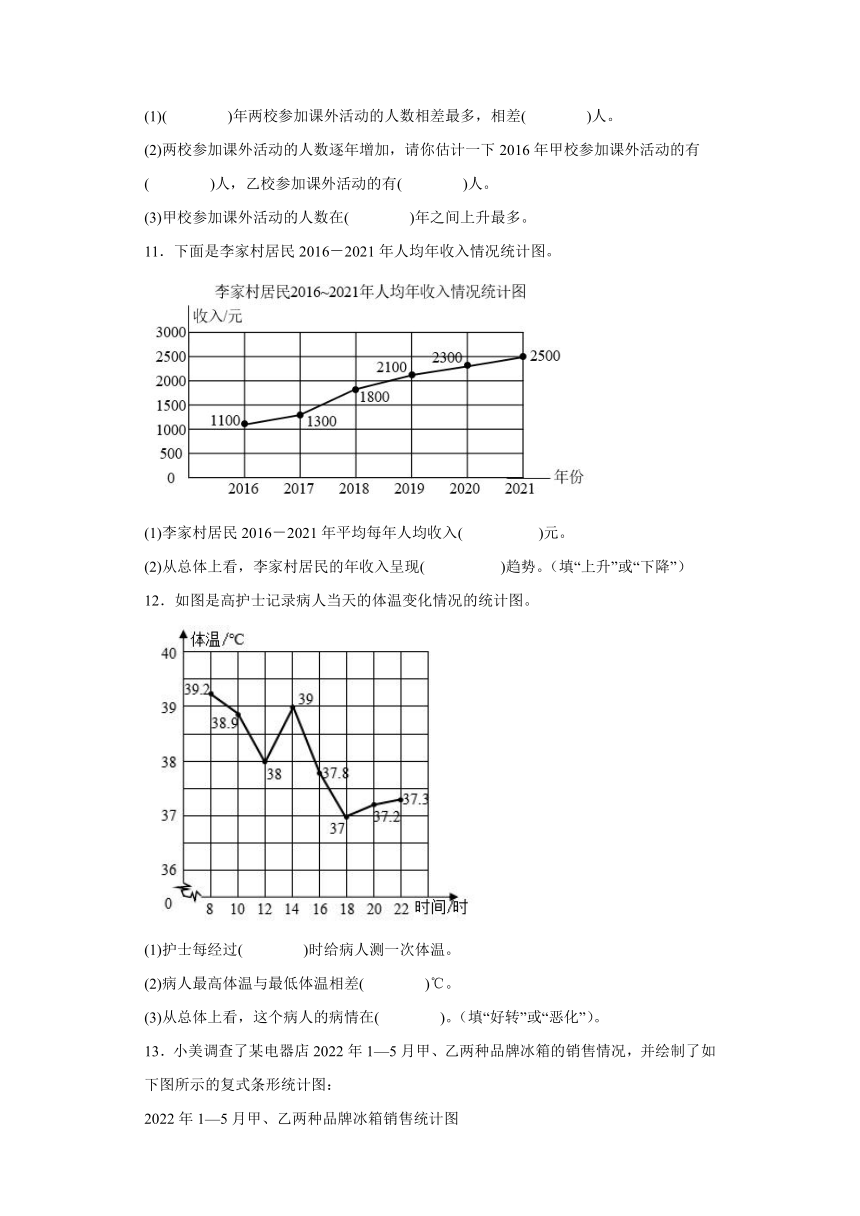
3.如图是某楼房上的蓄水池横截面图,分为深水区和浅水区,如果这个蓄水池以固定的流量注水,下图能表示水的最大深度h和注水时间t之间的关系是( )。
A. B. C. D.
4.一只兔子和一条小狗同时从同一地点向相同方向出发,它们的运动距离与时间关系图像如图所示,则关于该图像下列说法正确的是( )。
A.小狗的速度始终比兔子快 B.在前5秒内,小狗比兔子快
C.图中段表明小狗的速度是 D.整个过程中小狗和兔子的平均速度相同
5.用折线统计图反映( )比较合适。
A.某校各年级在校人数
B.南京某一天的气温变化情况
C.水果店4月份各类水果的销售量
6.洗衣机在洗涤衣服时,每浆洗一遍都经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水)。在这三个过程中,洗衣机内的水量y(升)与浆洗一遍的时间x(分)之间函数关系的图象大致为( )。
A. B.
C. D.
7.下面的信息资料中,最适合用折线统计图表示的是( )。
A.实验小学五年级各班级学生人数。
B.泗洪地区2020年每个季度降水量情况。
C.张小楠6~12岁身高变化情况。
D.某品牌汽车2020年各种车型的销售情况。
8.以下几种情况,最适合用折线统计图统计的是( )。
A.某公司销售业绩增减变化情况 B.六年级各班人数
C.各类图书本数 D.各类支出占家庭支出的百分比
二、填空题(16分)
9.学校要统计上周五每个年级学生借图书的本数可选用( )统计图;要统计上月五年级学生每周借书量的变化情况应选用( )统计图;要统计比较上月五(1)班、五(2)班学生每周借书量的变化情况应选用( )统计图。
10.某市甲,乙两所学校学生参加课外活动情况统计图如图。
(1)( )年两校参加课外活动的人数相差最多,相差( )人。
(2)两校参加课外活动的人数逐年增加,请你估计一下2016年甲校参加课外活动的有( )人,乙校参加课外活动的有( )人。
(3)甲校参加课外活动的人数在( )年之间上升最多。
11.下面是李家村居民2016-2021年人均年收入情况统计图。
(1)李家村居民2016-2021年平均每年人均收入( )元。
(2)从总体上看,李家村居民的年收入呈现( )趋势。(填“上升”或“下降”)
12.如图是高护士记录病人当天的体温变化情况的统计图。
(1)护士每经过( )时给病人测一次体温。
(2)病人最高体温与最低体温相差( )℃。
(3)从总体上看,这个病人的病情在( )。(填“好转”或“恶化”)。
13.小美调查了某电器店2022年1—5月甲、乙两种品牌冰箱的销售情况,并绘制了如下图所示的复式条形统计图:
2022年1—5月甲、乙两种品牌冰箱销售统计图
(1)( )月份两种品牌冰箱的销量相差最小,此时相差( )台。
(2)从总体情况来看,甲品牌冰箱销量呈现( )趋势,乙品牌冰箱销量呈现( )趋势。如果老板打算再购进这两种冰箱中的一种,他应该购进( )品牌的冰箱更合适。
(3)甲品牌冰箱1—5月平均每月销售( )台。
14.如图是某厂近几年售出的电热水器和太阳能热水器的销售情况。
(1)2016年一共销售两种热水器( )台。
(2)销售电热水器最多的是( )年,与同年销售的太阳能热水器比,相差( )台。
(3)2021年销售的( )热水器多;销售的电热水器与太阳能热水器台数最接近的是( )年。
(4)( )热水器从2016年到2018年的销售情况呈上升趋势,从2018年到2021年的销售情况呈下降趋势,( )热水器从2016年到2021年的销售情况一直呈上升趋势。
15.填一填。
(1)货车先出发( )小时。
(2)货车平均每小时行( )千米;客车平均每小时行( )千米。
(3)客车出发( )小时追上货车。
16.小明从家出发去6千米远的文景公园游玩,请根据折线图回答问题。
(1)小明从出发至回到家,一共用了( )小时,在公园玩了( )分钟。
(2)小明回家的速度是( )千米/时。
三、判断题(10分)
17.某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。( )
18.折线统计图能清晰地显示出数量的增减变化情况。( )
19.折线统计图最大的特点是可以反映出数量的多少。( )
20.折线统计图的折线越“陡”,说明变化越大;折线越“平”,变化越小。( )
21.表示一位病人一天内体温变化情况,制作条形统计图比较合适。( )
四、解方程(10分)
22.解方程。
36x+52x=220 7.8x-2.3x=1.1
6x+9x=2.25 0.8x-1.5×3=4.5
五、解答题(48分)
23.如表是甲乙两种树生长情况统计表。
(1)根据统计表将下面的统计图补充完整
(2)从开始植树到第七年,生长速度较快的是( )。(填“甲树”或“乙树”)
(3)生长到第( )年,两棵树的高度都是8米。
24.“双减”政策实施以来,丰富多彩的社团活动受到了学生们的热烈欢迎。下面是平城区某小学篮球社团精英队和先锋队的五场比赛得分情况统计表。
(1)请你根据表中的数据,完成下面折线统计图。
平城区某小学篮球社团精英队和先锋队的五场比赛得分情况统计图
(2)两个篮球队第一场比赛时成绩相差 分,第五场成绩相差 分。
(3)两队成绩呈现什么变化趋势?
(4)你能预测下一场两个篮球队的比赛结果吗?
25.下面是大同市2021年4月1日~7日气温统计表。(单位:℃)
(1)请你根据表中的数据,完成下面折线统计图。
(2)在4月1日~7日中,( )日气温最低,( )日气温最高。
(3)在4月1日~7日中,温差最大的是( )日,( )日和( )的温差一样。
(4)在4月1日~7日相邻的两天中,从( )日到( )日温度下降最快。
26.某地2022年3月9日至3月15日新冠疫情新增确诊人数统计如下表:
日期 9日 10日 11日 12日 13日 14日 15日
人数/人 20 17 8 7 6 4 1
(1)根据统计表中的信息,把下面的统计图接着绘制完。
(2)图中每格代表( )人,新增确诊人数情况总体呈现( )趋势。
(3)这7天,共新增确诊( )人,平均每天新增确诊( )人,加上3月8日新增确诊人数后,8天的平均新增确诊人数是10人,3月8日新增确诊( )人。
27.2020年新冠肺炎疫情期间,口罩厂向红星医院捐赠口罩:1月捐赠1000箱,2月捐赠1600箱,3月捐赠1900箱,4月捐赠1300箱,5月捐赠1100箱。
①根据以上信息,补充并画出折线统计图。
口罩厂每月捐赠红星医院口罩数量统计图
②纵轴表示( ),横轴表示( )。
③从折线统计图中你有什么发现?
④一年来,面对疫情,我们全国一心,众志成城,取得阶段性的伟大胜利,春节将至,面对如今各地疫情的星星之火,作为小学生,我们应该怎么做?
28.武汉某出租车2021年6—11月收入支出的统计图。请观察后回答
(1)这辆出租车赚钱的月份有( ),亏钱的月份有( )。
(2)赚钱最多的是哪个月?赚了多少万元?
(3)6个月以来,这辆车平均每个月收入是多少?
(4)武汉2021年7月再次出现新冠感染者,请结合疫情分析一下为什么这六个月出租车的收入会出现这样的结果?
29.下面是某书店1~6月份《青铜葵花》和《昆虫记》两种图书销售情况统计图,请根据图中信息解决下列问题。
(1)《青铜葵花》( )月销售量最少,《昆虫记》( )月销售量最多。
(2)《青铜葵花》和《昆虫记》销售量相差最大的是( )月,相差( )册。
(3)《昆虫记》销售量增长最快的是( )。(请在括号里填写正确选项对应的字母)
A.2月 B.5月 C.6月
30.甲、乙两车同时从A、B两地相向而行。设两车行驶的时间为t(时),两车离A地的距离为s(千米),s与t的关系如图所示。若A、B两地相距400千米,请解答下列问题:
(1)甲、乙两车出发几小时后相遇?
(2)甲车行驶多长时间后两车相距120千米?
参考答案:
1.A
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;复式统计表可以表示多组数据;据此解答。
【详解】要反映2021年上半年凤凰小学每月用水量的变化情况,应选用折线统计图。
故答案为:A
【点睛】利用它们各自的特征进行解答。
2.B
【分析】折线统计图的特征:能够清楚的反映数量的增减变化情况,条形统计图的特征:能够清楚的反映数量的多少,由此即可选择。
【详解】A.实验小学五年级各班学生人数,反映数量的多少,用条形统计图;
B.张晓明6~12岁身高变化情况,反映数量的增减变化情况,用折线统计图;
C.学校图书室各类图书的数量,反映数量的多少,用条形统计图;
D.某品牌汽车2021年各种车型的销售数量,反映数量的多少,用条形统计图。
故答案为:B
【点睛】本题主要考查条形统计图和折线统计图的特点,熟练掌握它们的特点并灵活运用。
3.B
【分析】根据图可知,下半部分的体积比较大,上半部分的体积比较小,所以下班部分的注水高度上升的会比上半部分的注水高度涨的慢,由此即可选择。
【详解】由分析可知:水的最大深度h与时间t之间的关系是先慢后快,如图所示:
。
故答案为:B
【点睛】此题考查根据几何图形的性质确定图象,解答此题关键是能根据几何图形和图形上的数据分析得出所对应比例的类型和所需要的条件,结合实际意义画出正确的图象。
4.D
【分析】A.由于在3秒到5秒的时候小狗是没有进行运动,兔子在进行移动,所以此时的兔子速度比小狗快;
B.在前5秒,兔子在相同时间内通过的路程比小狗的路程多,根据公式:速度=路程÷时间,由此即可判断;
C.由于BC段的时候小狗处于没有运动的时候,它是没有速度的,由此即可判断;
D.根据公式可知:路程÷时间=速度,它们都走了8米,都用了8秒,由此即可判断。
【详解】由分析得:
A.在3秒到5秒时,小狗没有运动,所以此时兔子速度比小狗快;原说法错误;
B.前5秒兔子走的路程比小狗多,所以兔子比小狗快,原说法错误;
C.BC段时小狗速度为0米/秒,原说法错误;
D.整个过程中两个动物走的路程相同,所用时间相同,所以平均速度相同,原说法正确。
故答案为:D
【点睛】本题主要考查折线统计图的分析,学会分析折线统计图是解题的关键。
5.B
【分析】折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;据此进行解答即可。
【详解】A.反映某校各年级在校人数的情况,用条形统计图比较合适;
B.反映南京某一天的气温变化情况,用折线统计图比较合适;
C.反映水果店4月份各类水果的销售量,用条形统计图比较合适。
故答案为:B
【点睛】此题应根据条形、折线统计图的特点进行分析、解答。
6.C
【分析】因为洗衣机工作前洗衣机内无水,所以A,B两选项不正确;又因为洗衣机最后排完水,水量要为0,所以D选项不正确;据此解答。
【详解】根据分析知:
只有C选项的图示表明了注水、清洗、排水三个连续过程,符合题意。
所以选项C正确。
故答案为:C。
【点睛】本题考查了对折线统计图的理解能力,看折线统计图要理解两个变量的变化情况。
7.C
【分析】折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况,据此解答。
【详解】A.要表示实验小学五年级各班级学生人数,用条形统计图比较合适;
B.要表示泗洪地区2020年每个季度降水量情况,用条形统计图比较合适;
C.要反映张小楠6~12岁身高变化情况,用折线统计图最合适;
D.要表示某品牌汽车2020年各种车型的销售情况,用条形统计图比较合适。
故正确答案为:C
【点睛】要牢固掌握条形统计图和折线统计图的特点,根据需要选择合适的统计图。
8.A
【分析】根据统计图的特征:折线统计图不但可以表示出数量的多少,而且还能够清楚地表示出数量增减变化的情况,可以直观地反映这种变化以及各组之间的差别;条形统计图可以看出数量的多少;扇形统计图可以表示出各个部分数量与总数之间的关系,据此解答。
【详解】A.某公司销售业绩增减变化情况最适合用折线统计图;
B.六年级各班人数最适合用条形统计图;
C.各类图书本数最适合用条形统计图;
D.各类支出占家庭支出的百分比最适合用扇形统计图。
故答案为:A
9. 条形 折线 复式折线
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;据此解答。
【详解】学校要统计上周五每个年级学生借图书的本数可选用条形统计图;要统计上月五年级学生每周借书量的变化情况应选用折线统计图;要统计比较上月五(1)班、五(2)班学生每周借书量的变化情况应选用复式折线统计图。
【点睛】本题应根据条形统计图。折线统计图和复式折线统计图的各自的特征进行解答。
10.(1) 2015 750
(2) 2700 1500
(3)2014到2015
【分析】(1)分别计算出每年两校参加课外活动的相差人数,再比较即可;
(2)估算合理即可,例如甲校前一年增加了700人,可以估算2016年也增加700人,乙校每年增加250人,则估算2016年也增加250人。
(3)分别计算甲校每年比前一年增加的数量,再比较即可。
【详解】(1)2012年:600-500=100(人)
2013年:1000-750=250(人)
2014年:1300-1000=300(人)
2015年:2000-1250=750(人)
100<250<300<750
2015年两校参加课外活动的人数相差最多,相差750人。
(2)2000-1300=700(人)
2000+700=2700(人)
1250-1000=250(人)
1250+250=1500(人)
2016年甲校参加课外活动的大约有2700人,乙校参加课外活动的有1500人。
(3)1000-600=400(人)
1300-1000=300(人)
2000-1300=700(人)
300<400<700
甲校参加课外活动的人数在2014到2015年之间上升最多。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1)1850
(2)上升
【分析】(1)根据求平均数的方法,先用加法求出2016-2021年的总收入,然后用除法解答即可。
(2)从总体上看,李家村居民的年收入每年都在增长,年收入呈现上升趋势。
【详解】(1)(1100+1300+1800+2100+2300+2500)÷6
=11100÷6
=1850(元)
李家村居民2016-2021年平均每年人均收入(1850 )元。
(2)从总体上看,李家村居民的年收入呈现(上升)趋势。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
12.(1)2
(2)2.2
(3)好转
【分析】(1)通过观察统计图直接回答问题。
(2)根据求一个数比另一个数多或少几,用最高体温减去最低体温解答。
(3)人的正常体温是37℃,通过统计图可知,这个病人的病情在好转;据此解答即可。
【详解】(1)护士每经过2时给病人测一次体温。
(2)39.2-37=2.2(℃)
病人最高体温与最低体温相差2.2℃。
(3)从总体上看,温度在下降,这个病人的病情在好转。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
13.(1) 4 2
(2) 下降 上升 乙
(3)57
【分析】(1)观察折线统计图可知,同一月份数据越接近,说明甲、乙两种品牌销量差越小,用较大值减去较小值即可;
(2)由图可知,实线表示甲冰箱的销量,虚线表示乙冰箱的销量,观察两种冰箱销量的走势图即可判断其变化趋势,进而确定应该购进的冰箱品牌;
(3)用甲冰箱5个月的销售总量除以5即可。
【详解】(1)53-51=2(台)
4月份两种品牌冰箱的销量相差最小,此时相差2台。
(2)从总体情况来看,甲品牌冰箱销量呈现下降趋势,乙品牌冰箱销量呈现上升趋势,如果老板打算再购进这两种冰箱中的一种,他应该购进甲品牌的冰箱更合适。
(3)(65+60+57+53+50)÷5
=285÷5
=57(台)
甲品牌冰箱1—5月平均每月销售57台。
【点睛】本题考查了从统计图中读出信息并根据信息解决问题的能力。
14.(1)1050
(2) 2018 370
(3) 太阳能 2019
(4) 电 太阳能
【分析】(1)观察统计图,找出2016年两种热水器销售的台数,再相加,即可;
(2)观察统计图,找出电热水器哪年销售最多;再找出同年太阳能热水器销售台数,再用销售电热水器的台数减去太阳能热水器的台数,即可;
(3)观察统计图,找出2021年哪种热水器销量多,再找出销售的电热水器与太阳能热水器台数最接近的是哪年;
(4)观察统计图,找出热水器从2016年到2018年的销售情况呈上升趋势,从2018年到2021年的销售情况呈下降趋势,哪种热水器从2016年到2021年的销售情况一直呈上升趋势即可。
【详解】(1)750+300=1050(台)
2016年一共销售两种热水器1050台;
(2)1050-680=370(台)
销售电热水器最多的是2018年,与同年销售的太阳能热水器比,相差370台;
(3)2021年销售的太阳能热水器多;销售的电热水器与太阳能热水器台数最接近的是2019年;
(4)电热水器从2016年到2018年的销售情况呈上升趋势,从2018年到2021年的销售情况呈下降趋势,太阳能热水器从2016年到2021年的销售情况一直呈上升趋势
【点睛】本题考查复式折线统计图的实际应用,根据统计图提供的信息解答问题的能力。
15.(1)2
(2) 60 30
(3)2
【分析】(1)观察折线统计图可知,货车的出发时间是0时,客车的出发时间是2时,据此解答;
(2)客车3小时行了90千米,货车7小时行了420千米,根据路程÷时间=速度,据此计算即可;
(3)根据速度×时间=路程,据此求出客车和货车开始相距的距离,然后根据路程÷速度差=追及时间,据此计算即可。
(1)
2-0=2(小时)
货车先出发2小时。
(2)
420÷7=60(千米)
90÷3=30(千米)
货车平均每小时行60千米;客车平均每小时行30千米。
(3)
30×2÷(60-30)
=60÷30
=2(小时)
客车出发2小时追上货车。
【点睛】本题考查折线统计图,通过统计图分析出相应的数据是解题的关键。
16.(1) 2 30
(2)12
【分析】(1)用结束时间-开始时间=经过时间,代入数据,求出一个用的时间,再根据统计图,1时到2时平均分成6份,60÷6=10分钟,每一小格是10分钟;求出小明在公园玩的时间;
(2)根据速度=距离÷时间,根据统计图,找出小明从公园到家的距离和时间,即可求出小明回家的速度。
(1)
3-1=2(小时);60÷6=10(分钟)
10×3=30(分钟)
小明从出发至回到家,一共用了2小时,在公园玩了30分钟。
(2)
10×3=30(分钟)
30分钟=0.5小时
6÷0.5=12(千米/时)
【点睛】本题考查折线统计图的应用,以及根据统计图提供的信息,解答问题能力。
17.√
【分析】折线统计图:能够反应数量的多少,能够反映出数量的增减变化情况;条形统计图:能够清楚的反映出数量的多少,由此即可判断。
【详解】由分析可知:
某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。原题说法正确。
故答案为:√
【点睛】本题主要考查统计图的特点,熟练掌握折线统计图和条形统计图的特点并灵活运用。
18.√
【详解】折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况。
故答案为:√
19.×
【分析】折线统计图的特点是不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此判断。
【详解】折线统计图的特点是不仅容易看出数量的多少,而且能反映数量的增减变化情况;
故答案为:×。
【点睛】此题考查的是折线统计图的特点的掌握情况。
20.√
【分析】折线统计图的折线越“陡”说明数据之间的差越大,变化越大;折线越“平”说明数据之间的差越小,则变化越小,据此判断。
【详解】折线统计图的折线越“陡”,说明变化越大;折线越“平”,变化越小。原题说法正确。
【点睛】此题考查折线统计图的特点,利用折线统计图这一特点可以直观解决很多问题。
21.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】根据统计图的特点可知:表示一位病人一天内体温变化情况,制作折线统计图比较合适;所以原题说法错误。
故答案为:×。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
22.x=2.5;x=0.2
x=0.15;x=11.25
【分析】根据题型,先将等号左边的式子能化简的先化简,然后再把x的系数化一即可,如将36x+52x=220化简为88x=220,然后等号左右两边同时除以88即可解答。
【详解】36x+52x=220
解:88x=220
x=2.5
7.8x-2.3x=1.1
解:5.5x=1.1
x=0.2
6x+9x=2.25
解:15x=2.25
x=0.15
0.8x-1.5×3=4.5
解:0.8x-4.5=4.5
0.8x=4.5+4.5
x=9÷0.8
x=11.25
【点睛】解方程时,先把相同的项合并在一起,即把含有x的项放在等号的左边,把常数项放在等号的右边,然后等号两边同时除以x前面的系数,即可解得x的值。
23.(1)见详解
(2)乙树
(3)10
【分析】(1)根据统计表提供的数据,完成统计图;
(2)观察统计图第七年后,哪种树生长的快;
(3)观察统计图,找出第几年两棵树的高度都是8米。
【详解】(1)
(2)从开始植树到第七年,生产速度较快的是乙树;
(3)生长到第10年,两个数的高度都是8米。
【点睛】本题考查折线统计图的填充。关键是利用所给数据完成统计图并回答问题。
24.(1)见解答;
(2)4;4;
(3)精英队的成绩呈现持续上升的趋势,先锋队的成绩呈现先上升再下降后上升的变化趋势。
(4)我预测下一场两个篮球队的比赛结果是:精英队获胜。
【分析】(1)根据表中数直接描点画图即可;
(2)找出第一场比赛时的成绩求差即可;找出第五场比赛时的成绩求差即可;
(3)根据折线统计图的变化趋势解答即可;
(4)根据折线统计图变化趋势直接解答即可。
【详解】(1)统计图如下:
(2)50-46=4(分)
55-51=4(分)
答:两个篮球队第一场比赛时成绩相差4分,第五场成绩相差4分。
(3)精英队的成绩呈现持续上升的趋势,先锋队的成绩呈现先上升再下降后上升的变化趋势。
(4)我预测下一场两个篮球队的比赛结果是:精英队获胜。
【点睛】本题主要考查统计图表的综合应用。
25.(1)见详解。
(2)3;1
(3)2;3;4
(4)2;3
【分析】(1)制作折线统计图时,先从列中找到项目,再从行中找到对应的数量高度点个点,然后顺次连点成线,复式图虚实线分开表示。
(2)比较在4月1日~7日中各天的最高和最低气温,作判断。
(3)比较在4月1日~7日中每天的温差,作判断。
(4)比较4月1日~7日相邻的两天中气温下降最大的,作判断。
【详解】(1)如图:
(2)在4月1日~7日中,3日气温最低,1日气温最高。
(3)15-2=13℃
13-(﹣2)=15℃
7-(﹣3)=10℃
12-2=10℃
14-0=14℃
11-3=8℃
13-1=12℃
答:在4月1日~7日中,温差最大的是2日,3日和4的温差一样。
(4)在4月1日~7日相邻的两天中,从2日到3日温度下降最快。
【点睛】本题考查了学生动手操作能力及从统计图中获取信息的意识。
26.(1)见详解
(2)2;下降
(3)63;9;17
【分析】(1)折线统计图中横轴表示日期,纵轴表示人数,根据统计表中的数据准确描出各天对应的人数,再依次连接各点;
(2)观察折线统计图的纵轴,每格代表2人,新增确诊人数情况总体呈现下降趋势;
(3)用(20+17+8+7+6+4+1)求出这7天,共新增确诊多少人;用共新增确诊的人数除以7,求出平均每天新增确诊多少人;用8乘10,求出8天共新增确诊人数,再减去3月9日到3月15日共新增确诊人数,求出3月8日新增确诊多少人。
【详解】(1)如下图:
(2)图中每格代表2人,新增确诊人数情况总体呈现下降趋势。
(3)20+17+8+7+6+4+1
=37+15+10+1
=52+11
=63(人)
63÷7=9(人)
8×10=80(人)
80-63=17(人)
这7天,共新增确诊63人,平均每天新增确诊9人,加上3月8日新增确诊人数后,8天的平均新增确诊人数是10人,3月8日新增确诊17人。
【点睛】理解并掌握折线统计图、统计表的特点及作用,并且能够根据统计图表提供的信息解决有关实际问题是解答题目的关键。
27.①见详解
②数量;时间
③3月捐赠数量最多(答案不唯一)
④多居家运动,少聚集(答案不唯一)
【分析】①确定纵轴和横轴每一个单位的长度,数据都超过1000,起始格表示1000箱,上边每格表示100比较合适;根据各数量的多少,在方格图的纵线或横线(或纵、横的交点)上描出表示数量多少的点;把各点用线段顺次连接起来,标上数据即可。
②观察统计图,竖直方向的叫纵轴,水平方向的叫横轴,看两条轴即可确定分别表示什么。
③答案不唯一,合理即可。
④答案不唯一,合理即可。
【详解】①由分析得:
口罩厂每月捐赠红星医院口罩数量统计图
②纵轴表示数量;横轴表示时间。
③发现3月捐赠数量最多。
④答案不唯一,如多居家运动,少聚集,勤洗手等。
【点睛】折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
28.(1)6月、9月、10月、11月;7月、8月
(2)11月;0.72万元
(3)0.73万元
(4)见详解(答案不唯一)
【分析】(1)实线和虚线分别表示收入和支出,当实线高于虚线时,说明收入大于支出,也就是赚钱了;相反,就是亏钱了。
(2)根据折线统计图可以知道,赚钱最多的月份是11月,再进行具体计算即可确定6月赚了多少钱。
(3)收入在图中是用实线表示,所以找到实线上的这些点所对应的金额,然后先相加再除以月份即可。
(4)根据统计图中折线的走势和实际情况分析数据产生变化的原因。
【详解】由分析可知:
(1)这辆出租车赚钱的月份有6月、9月、10月、11月,亏钱的月份有7月、8月。
(2)1.33-0.61=0.72(万元)
答:赚钱最多的月是11月,赚了0.72万元。
(3)(0.9+0.16+0.13+0.58+1.28+1.33)÷6
=4.38÷6
=0.73(万元)
答:这两车的平均收入是0.73万元。
(4)由于疫情影响,在7月和8月,人们出行量极少,因此出租车收入降到最低,从9月起,由于疫情逐渐好转,人们出行量逐渐增加,出租车的收入也就随之增加。(答案不唯一)
【点睛】本题主要考查折线统计图的实际应用,学会从统计图中找出有用的数学信息是解题关键。
29.(1) 1 6
(2) 6 120
(3)B
【分析】(1)实线表示《青铜葵花》的销售情况,虚线表示《昆虫记》的销售情况,折点越高销量越多,折点越低销量越少;
(2)两条折线之间的距离越大两种书的销量相差越大,根据图中数据求出6月两种书的销量之差;
(3)折线统计图中折线越陡销量增长越快,折线越缓销量增长越慢,据此解答。
(1)
《青铜葵花》1月销售量最少,《昆虫记》6月销售量最多。
(2)
450-330=120(册)
由图可知,《青铜葵花》和《昆虫记》销售量相差最大的是6月,相差120册。
(3)
分析可知,《昆虫记》销售量增长最快的是5月。
故答案为:B
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
30.(1)小时
(2)小时或小时
【分析】由题意可得A、B两地相距400千米,行驶完全程甲用5小时,乙用4小时。
(1)先根据速度=路程÷时间,求出甲、乙两车速度,再用总路程除以速度和,即可得甲、乙两车出发几小时后相遇。
(2)相遇前,用总路程减120千米,再除以速度和,即可得甲车行驶多长时间后两车相距120千米;相遇后,用总路程加120千米,再除以速度和,即可得甲车行驶多长时间后两车相距120千米。
【详解】(1)400÷(400÷5+400÷4)
=400÷(80+100)
=400÷180
=(小时)
答:甲、乙两车出发小时后相遇。
(2)相遇前:
(400-120)÷(400÷5+400÷4)
=280÷180
=(小时)
相遇后:
(400+120)÷(400÷5+400÷4)
=520÷180
=(小时)
答:甲车行驶小时或小时后两车相距120千米。
【点睛】本题主要考查复式折线统计图的应用,关键根据统计图找到解决问题的信息,解决问题。
《折线统计图》
学校:___________姓名:___________班级:___________
一、选择题(16分)
1.要反映2021年上半年凤凰小学每月用水量的变化情况,应选用( )。
A.折线统计图 B.条形统计图 C.复式统计表 D.无法确定
2.下面的信息资料中,最适合用折线统计图表示的是( )。
A.实验小学五年级各班学生人数 B.张小明6~12岁身高变化情况
C.学校图书室各类图书的数量 D.某品牌汽车2021年各种车型的销售数量
3.如图是某楼房上的蓄水池横截面图,分为深水区和浅水区,如果这个蓄水池以固定的流量注水,下图能表示水的最大深度h和注水时间t之间的关系是( )。
A. B. C. D.
4.一只兔子和一条小狗同时从同一地点向相同方向出发,它们的运动距离与时间关系图像如图所示,则关于该图像下列说法正确的是( )。
A.小狗的速度始终比兔子快 B.在前5秒内,小狗比兔子快
C.图中段表明小狗的速度是 D.整个过程中小狗和兔子的平均速度相同
5.用折线统计图反映( )比较合适。
A.某校各年级在校人数
B.南京某一天的气温变化情况
C.水果店4月份各类水果的销售量
6.洗衣机在洗涤衣服时,每浆洗一遍都经历了注水、清洗、排水三个连续过程(工作前洗衣机内无水)。在这三个过程中,洗衣机内的水量y(升)与浆洗一遍的时间x(分)之间函数关系的图象大致为( )。
A. B.
C. D.
7.下面的信息资料中,最适合用折线统计图表示的是( )。
A.实验小学五年级各班级学生人数。
B.泗洪地区2020年每个季度降水量情况。
C.张小楠6~12岁身高变化情况。
D.某品牌汽车2020年各种车型的销售情况。
8.以下几种情况,最适合用折线统计图统计的是( )。
A.某公司销售业绩增减变化情况 B.六年级各班人数
C.各类图书本数 D.各类支出占家庭支出的百分比
二、填空题(16分)
9.学校要统计上周五每个年级学生借图书的本数可选用( )统计图;要统计上月五年级学生每周借书量的变化情况应选用( )统计图;要统计比较上月五(1)班、五(2)班学生每周借书量的变化情况应选用( )统计图。
10.某市甲,乙两所学校学生参加课外活动情况统计图如图。
(1)( )年两校参加课外活动的人数相差最多,相差( )人。
(2)两校参加课外活动的人数逐年增加,请你估计一下2016年甲校参加课外活动的有( )人,乙校参加课外活动的有( )人。
(3)甲校参加课外活动的人数在( )年之间上升最多。
11.下面是李家村居民2016-2021年人均年收入情况统计图。
(1)李家村居民2016-2021年平均每年人均收入( )元。
(2)从总体上看,李家村居民的年收入呈现( )趋势。(填“上升”或“下降”)
12.如图是高护士记录病人当天的体温变化情况的统计图。
(1)护士每经过( )时给病人测一次体温。
(2)病人最高体温与最低体温相差( )℃。
(3)从总体上看,这个病人的病情在( )。(填“好转”或“恶化”)。
13.小美调查了某电器店2022年1—5月甲、乙两种品牌冰箱的销售情况,并绘制了如下图所示的复式条形统计图:
2022年1—5月甲、乙两种品牌冰箱销售统计图
(1)( )月份两种品牌冰箱的销量相差最小,此时相差( )台。
(2)从总体情况来看,甲品牌冰箱销量呈现( )趋势,乙品牌冰箱销量呈现( )趋势。如果老板打算再购进这两种冰箱中的一种,他应该购进( )品牌的冰箱更合适。
(3)甲品牌冰箱1—5月平均每月销售( )台。
14.如图是某厂近几年售出的电热水器和太阳能热水器的销售情况。
(1)2016年一共销售两种热水器( )台。
(2)销售电热水器最多的是( )年,与同年销售的太阳能热水器比,相差( )台。
(3)2021年销售的( )热水器多;销售的电热水器与太阳能热水器台数最接近的是( )年。
(4)( )热水器从2016年到2018年的销售情况呈上升趋势,从2018年到2021年的销售情况呈下降趋势,( )热水器从2016年到2021年的销售情况一直呈上升趋势。
15.填一填。
(1)货车先出发( )小时。
(2)货车平均每小时行( )千米;客车平均每小时行( )千米。
(3)客车出发( )小时追上货车。
16.小明从家出发去6千米远的文景公园游玩,请根据折线图回答问题。
(1)小明从出发至回到家,一共用了( )小时,在公园玩了( )分钟。
(2)小明回家的速度是( )千米/时。
三、判断题(10分)
17.某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。( )
18.折线统计图能清晰地显示出数量的增减变化情况。( )
19.折线统计图最大的特点是可以反映出数量的多少。( )
20.折线统计图的折线越“陡”,说明变化越大;折线越“平”,变化越小。( )
21.表示一位病人一天内体温变化情况,制作条形统计图比较合适。( )
四、解方程(10分)
22.解方程。
36x+52x=220 7.8x-2.3x=1.1
6x+9x=2.25 0.8x-1.5×3=4.5
五、解答题(48分)
23.如表是甲乙两种树生长情况统计表。
(1)根据统计表将下面的统计图补充完整
(2)从开始植树到第七年,生长速度较快的是( )。(填“甲树”或“乙树”)
(3)生长到第( )年,两棵树的高度都是8米。
24.“双减”政策实施以来,丰富多彩的社团活动受到了学生们的热烈欢迎。下面是平城区某小学篮球社团精英队和先锋队的五场比赛得分情况统计表。
(1)请你根据表中的数据,完成下面折线统计图。
平城区某小学篮球社团精英队和先锋队的五场比赛得分情况统计图
(2)两个篮球队第一场比赛时成绩相差 分,第五场成绩相差 分。
(3)两队成绩呈现什么变化趋势?
(4)你能预测下一场两个篮球队的比赛结果吗?
25.下面是大同市2021年4月1日~7日气温统计表。(单位:℃)
(1)请你根据表中的数据,完成下面折线统计图。
(2)在4月1日~7日中,( )日气温最低,( )日气温最高。
(3)在4月1日~7日中,温差最大的是( )日,( )日和( )的温差一样。
(4)在4月1日~7日相邻的两天中,从( )日到( )日温度下降最快。
26.某地2022年3月9日至3月15日新冠疫情新增确诊人数统计如下表:
日期 9日 10日 11日 12日 13日 14日 15日
人数/人 20 17 8 7 6 4 1
(1)根据统计表中的信息,把下面的统计图接着绘制完。
(2)图中每格代表( )人,新增确诊人数情况总体呈现( )趋势。
(3)这7天,共新增确诊( )人,平均每天新增确诊( )人,加上3月8日新增确诊人数后,8天的平均新增确诊人数是10人,3月8日新增确诊( )人。
27.2020年新冠肺炎疫情期间,口罩厂向红星医院捐赠口罩:1月捐赠1000箱,2月捐赠1600箱,3月捐赠1900箱,4月捐赠1300箱,5月捐赠1100箱。
①根据以上信息,补充并画出折线统计图。
口罩厂每月捐赠红星医院口罩数量统计图
②纵轴表示( ),横轴表示( )。
③从折线统计图中你有什么发现?
④一年来,面对疫情,我们全国一心,众志成城,取得阶段性的伟大胜利,春节将至,面对如今各地疫情的星星之火,作为小学生,我们应该怎么做?
28.武汉某出租车2021年6—11月收入支出的统计图。请观察后回答
(1)这辆出租车赚钱的月份有( ),亏钱的月份有( )。
(2)赚钱最多的是哪个月?赚了多少万元?
(3)6个月以来,这辆车平均每个月收入是多少?
(4)武汉2021年7月再次出现新冠感染者,请结合疫情分析一下为什么这六个月出租车的收入会出现这样的结果?
29.下面是某书店1~6月份《青铜葵花》和《昆虫记》两种图书销售情况统计图,请根据图中信息解决下列问题。
(1)《青铜葵花》( )月销售量最少,《昆虫记》( )月销售量最多。
(2)《青铜葵花》和《昆虫记》销售量相差最大的是( )月,相差( )册。
(3)《昆虫记》销售量增长最快的是( )。(请在括号里填写正确选项对应的字母)
A.2月 B.5月 C.6月
30.甲、乙两车同时从A、B两地相向而行。设两车行驶的时间为t(时),两车离A地的距离为s(千米),s与t的关系如图所示。若A、B两地相距400千米,请解答下列问题:
(1)甲、乙两车出发几小时后相遇?
(2)甲车行驶多长时间后两车相距120千米?
参考答案:
1.A
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;复式统计表可以表示多组数据;据此解答。
【详解】要反映2021年上半年凤凰小学每月用水量的变化情况,应选用折线统计图。
故答案为:A
【点睛】利用它们各自的特征进行解答。
2.B
【分析】折线统计图的特征:能够清楚的反映数量的增减变化情况,条形统计图的特征:能够清楚的反映数量的多少,由此即可选择。
【详解】A.实验小学五年级各班学生人数,反映数量的多少,用条形统计图;
B.张晓明6~12岁身高变化情况,反映数量的增减变化情况,用折线统计图;
C.学校图书室各类图书的数量,反映数量的多少,用条形统计图;
D.某品牌汽车2021年各种车型的销售数量,反映数量的多少,用条形统计图。
故答案为:B
【点睛】本题主要考查条形统计图和折线统计图的特点,熟练掌握它们的特点并灵活运用。
3.B
【分析】根据图可知,下半部分的体积比较大,上半部分的体积比较小,所以下班部分的注水高度上升的会比上半部分的注水高度涨的慢,由此即可选择。
【详解】由分析可知:水的最大深度h与时间t之间的关系是先慢后快,如图所示:
。
故答案为:B
【点睛】此题考查根据几何图形的性质确定图象,解答此题关键是能根据几何图形和图形上的数据分析得出所对应比例的类型和所需要的条件,结合实际意义画出正确的图象。
4.D
【分析】A.由于在3秒到5秒的时候小狗是没有进行运动,兔子在进行移动,所以此时的兔子速度比小狗快;
B.在前5秒,兔子在相同时间内通过的路程比小狗的路程多,根据公式:速度=路程÷时间,由此即可判断;
C.由于BC段的时候小狗处于没有运动的时候,它是没有速度的,由此即可判断;
D.根据公式可知:路程÷时间=速度,它们都走了8米,都用了8秒,由此即可判断。
【详解】由分析得:
A.在3秒到5秒时,小狗没有运动,所以此时兔子速度比小狗快;原说法错误;
B.前5秒兔子走的路程比小狗多,所以兔子比小狗快,原说法错误;
C.BC段时小狗速度为0米/秒,原说法错误;
D.整个过程中两个动物走的路程相同,所用时间相同,所以平均速度相同,原说法正确。
故答案为:D
【点睛】本题主要考查折线统计图的分析,学会分析折线统计图是解题的关键。
5.B
【分析】折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;据此进行解答即可。
【详解】A.反映某校各年级在校人数的情况,用条形统计图比较合适;
B.反映南京某一天的气温变化情况,用折线统计图比较合适;
C.反映水果店4月份各类水果的销售量,用条形统计图比较合适。
故答案为:B
【点睛】此题应根据条形、折线统计图的特点进行分析、解答。
6.C
【分析】因为洗衣机工作前洗衣机内无水,所以A,B两选项不正确;又因为洗衣机最后排完水,水量要为0,所以D选项不正确;据此解答。
【详解】根据分析知:
只有C选项的图示表明了注水、清洗、排水三个连续过程,符合题意。
所以选项C正确。
故答案为:C。
【点睛】本题考查了对折线统计图的理解能力,看折线统计图要理解两个变量的变化情况。
7.C
【分析】折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况,据此解答。
【详解】A.要表示实验小学五年级各班级学生人数,用条形统计图比较合适;
B.要表示泗洪地区2020年每个季度降水量情况,用条形统计图比较合适;
C.要反映张小楠6~12岁身高变化情况,用折线统计图最合适;
D.要表示某品牌汽车2020年各种车型的销售情况,用条形统计图比较合适。
故正确答案为:C
【点睛】要牢固掌握条形统计图和折线统计图的特点,根据需要选择合适的统计图。
8.A
【分析】根据统计图的特征:折线统计图不但可以表示出数量的多少,而且还能够清楚地表示出数量增减变化的情况,可以直观地反映这种变化以及各组之间的差别;条形统计图可以看出数量的多少;扇形统计图可以表示出各个部分数量与总数之间的关系,据此解答。
【详解】A.某公司销售业绩增减变化情况最适合用折线统计图;
B.六年级各班人数最适合用条形统计图;
C.各类图书本数最适合用条形统计图;
D.各类支出占家庭支出的百分比最适合用扇形统计图。
故答案为:A
9. 条形 折线 复式折线
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;据此解答。
【详解】学校要统计上周五每个年级学生借图书的本数可选用条形统计图;要统计上月五年级学生每周借书量的变化情况应选用折线统计图;要统计比较上月五(1)班、五(2)班学生每周借书量的变化情况应选用复式折线统计图。
【点睛】本题应根据条形统计图。折线统计图和复式折线统计图的各自的特征进行解答。
10.(1) 2015 750
(2) 2700 1500
(3)2014到2015
【分析】(1)分别计算出每年两校参加课外活动的相差人数,再比较即可;
(2)估算合理即可,例如甲校前一年增加了700人,可以估算2016年也增加700人,乙校每年增加250人,则估算2016年也增加250人。
(3)分别计算甲校每年比前一年增加的数量,再比较即可。
【详解】(1)2012年:600-500=100(人)
2013年:1000-750=250(人)
2014年:1300-1000=300(人)
2015年:2000-1250=750(人)
100<250<300<750
2015年两校参加课外活动的人数相差最多,相差750人。
(2)2000-1300=700(人)
2000+700=2700(人)
1250-1000=250(人)
1250+250=1500(人)
2016年甲校参加课外活动的大约有2700人,乙校参加课外活动的有1500人。
(3)1000-600=400(人)
1300-1000=300(人)
2000-1300=700(人)
300<400<700
甲校参加课外活动的人数在2014到2015年之间上升最多。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
11.(1)1850
(2)上升
【分析】(1)根据求平均数的方法,先用加法求出2016-2021年的总收入,然后用除法解答即可。
(2)从总体上看,李家村居民的年收入每年都在增长,年收入呈现上升趋势。
【详解】(1)(1100+1300+1800+2100+2300+2500)÷6
=11100÷6
=1850(元)
李家村居民2016-2021年平均每年人均收入(1850 )元。
(2)从总体上看,李家村居民的年收入呈现(上升)趋势。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
12.(1)2
(2)2.2
(3)好转
【分析】(1)通过观察统计图直接回答问题。
(2)根据求一个数比另一个数多或少几,用最高体温减去最低体温解答。
(3)人的正常体温是37℃,通过统计图可知,这个病人的病情在好转;据此解答即可。
【详解】(1)护士每经过2时给病人测一次体温。
(2)39.2-37=2.2(℃)
病人最高体温与最低体温相差2.2℃。
(3)从总体上看,温度在下降,这个病人的病情在好转。
【点睛】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
13.(1) 4 2
(2) 下降 上升 乙
(3)57
【分析】(1)观察折线统计图可知,同一月份数据越接近,说明甲、乙两种品牌销量差越小,用较大值减去较小值即可;
(2)由图可知,实线表示甲冰箱的销量,虚线表示乙冰箱的销量,观察两种冰箱销量的走势图即可判断其变化趋势,进而确定应该购进的冰箱品牌;
(3)用甲冰箱5个月的销售总量除以5即可。
【详解】(1)53-51=2(台)
4月份两种品牌冰箱的销量相差最小,此时相差2台。
(2)从总体情况来看,甲品牌冰箱销量呈现下降趋势,乙品牌冰箱销量呈现上升趋势,如果老板打算再购进这两种冰箱中的一种,他应该购进甲品牌的冰箱更合适。
(3)(65+60+57+53+50)÷5
=285÷5
=57(台)
甲品牌冰箱1—5月平均每月销售57台。
【点睛】本题考查了从统计图中读出信息并根据信息解决问题的能力。
14.(1)1050
(2) 2018 370
(3) 太阳能 2019
(4) 电 太阳能
【分析】(1)观察统计图,找出2016年两种热水器销售的台数,再相加,即可;
(2)观察统计图,找出电热水器哪年销售最多;再找出同年太阳能热水器销售台数,再用销售电热水器的台数减去太阳能热水器的台数,即可;
(3)观察统计图,找出2021年哪种热水器销量多,再找出销售的电热水器与太阳能热水器台数最接近的是哪年;
(4)观察统计图,找出热水器从2016年到2018年的销售情况呈上升趋势,从2018年到2021年的销售情况呈下降趋势,哪种热水器从2016年到2021年的销售情况一直呈上升趋势即可。
【详解】(1)750+300=1050(台)
2016年一共销售两种热水器1050台;
(2)1050-680=370(台)
销售电热水器最多的是2018年,与同年销售的太阳能热水器比,相差370台;
(3)2021年销售的太阳能热水器多;销售的电热水器与太阳能热水器台数最接近的是2019年;
(4)电热水器从2016年到2018年的销售情况呈上升趋势,从2018年到2021年的销售情况呈下降趋势,太阳能热水器从2016年到2021年的销售情况一直呈上升趋势
【点睛】本题考查复式折线统计图的实际应用,根据统计图提供的信息解答问题的能力。
15.(1)2
(2) 60 30
(3)2
【分析】(1)观察折线统计图可知,货车的出发时间是0时,客车的出发时间是2时,据此解答;
(2)客车3小时行了90千米,货车7小时行了420千米,根据路程÷时间=速度,据此计算即可;
(3)根据速度×时间=路程,据此求出客车和货车开始相距的距离,然后根据路程÷速度差=追及时间,据此计算即可。
(1)
2-0=2(小时)
货车先出发2小时。
(2)
420÷7=60(千米)
90÷3=30(千米)
货车平均每小时行60千米;客车平均每小时行30千米。
(3)
30×2÷(60-30)
=60÷30
=2(小时)
客车出发2小时追上货车。
【点睛】本题考查折线统计图,通过统计图分析出相应的数据是解题的关键。
16.(1) 2 30
(2)12
【分析】(1)用结束时间-开始时间=经过时间,代入数据,求出一个用的时间,再根据统计图,1时到2时平均分成6份,60÷6=10分钟,每一小格是10分钟;求出小明在公园玩的时间;
(2)根据速度=距离÷时间,根据统计图,找出小明从公园到家的距离和时间,即可求出小明回家的速度。
(1)
3-1=2(小时);60÷6=10(分钟)
10×3=30(分钟)
小明从出发至回到家,一共用了2小时,在公园玩了30分钟。
(2)
10×3=30(分钟)
30分钟=0.5小时
6÷0.5=12(千米/时)
【点睛】本题考查折线统计图的应用,以及根据统计图提供的信息,解答问题能力。
17.√
【分析】折线统计图:能够反应数量的多少,能够反映出数量的增减变化情况;条形统计图:能够清楚的反映出数量的多少,由此即可判断。
【详解】由分析可知:
某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。原题说法正确。
故答案为:√
【点睛】本题主要考查统计图的特点,熟练掌握折线统计图和条形统计图的特点并灵活运用。
18.√
【详解】折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况。
故答案为:√
19.×
【分析】折线统计图的特点是不仅容易看出数量的多少,而且能反映数量的增减变化情况;由此判断。
【详解】折线统计图的特点是不仅容易看出数量的多少,而且能反映数量的增减变化情况;
故答案为:×。
【点睛】此题考查的是折线统计图的特点的掌握情况。
20.√
【分析】折线统计图的折线越“陡”说明数据之间的差越大,变化越大;折线越“平”说明数据之间的差越小,则变化越小,据此判断。
【详解】折线统计图的折线越“陡”,说明变化越大;折线越“平”,变化越小。原题说法正确。
【点睛】此题考查折线统计图的特点,利用折线统计图这一特点可以直观解决很多问题。
21.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】根据统计图的特点可知:表示一位病人一天内体温变化情况,制作折线统计图比较合适;所以原题说法错误。
故答案为:×。
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
22.x=2.5;x=0.2
x=0.15;x=11.25
【分析】根据题型,先将等号左边的式子能化简的先化简,然后再把x的系数化一即可,如将36x+52x=220化简为88x=220,然后等号左右两边同时除以88即可解答。
【详解】36x+52x=220
解:88x=220
x=2.5
7.8x-2.3x=1.1
解:5.5x=1.1
x=0.2
6x+9x=2.25
解:15x=2.25
x=0.15
0.8x-1.5×3=4.5
解:0.8x-4.5=4.5
0.8x=4.5+4.5
x=9÷0.8
x=11.25
【点睛】解方程时,先把相同的项合并在一起,即把含有x的项放在等号的左边,把常数项放在等号的右边,然后等号两边同时除以x前面的系数,即可解得x的值。
23.(1)见详解
(2)乙树
(3)10
【分析】(1)根据统计表提供的数据,完成统计图;
(2)观察统计图第七年后,哪种树生长的快;
(3)观察统计图,找出第几年两棵树的高度都是8米。
【详解】(1)
(2)从开始植树到第七年,生产速度较快的是乙树;
(3)生长到第10年,两个数的高度都是8米。
【点睛】本题考查折线统计图的填充。关键是利用所给数据完成统计图并回答问题。
24.(1)见解答;
(2)4;4;
(3)精英队的成绩呈现持续上升的趋势,先锋队的成绩呈现先上升再下降后上升的变化趋势。
(4)我预测下一场两个篮球队的比赛结果是:精英队获胜。
【分析】(1)根据表中数直接描点画图即可;
(2)找出第一场比赛时的成绩求差即可;找出第五场比赛时的成绩求差即可;
(3)根据折线统计图的变化趋势解答即可;
(4)根据折线统计图变化趋势直接解答即可。
【详解】(1)统计图如下:
(2)50-46=4(分)
55-51=4(分)
答:两个篮球队第一场比赛时成绩相差4分,第五场成绩相差4分。
(3)精英队的成绩呈现持续上升的趋势,先锋队的成绩呈现先上升再下降后上升的变化趋势。
(4)我预测下一场两个篮球队的比赛结果是:精英队获胜。
【点睛】本题主要考查统计图表的综合应用。
25.(1)见详解。
(2)3;1
(3)2;3;4
(4)2;3
【分析】(1)制作折线统计图时,先从列中找到项目,再从行中找到对应的数量高度点个点,然后顺次连点成线,复式图虚实线分开表示。
(2)比较在4月1日~7日中各天的最高和最低气温,作判断。
(3)比较在4月1日~7日中每天的温差,作判断。
(4)比较4月1日~7日相邻的两天中气温下降最大的,作判断。
【详解】(1)如图:
(2)在4月1日~7日中,3日气温最低,1日气温最高。
(3)15-2=13℃
13-(﹣2)=15℃
7-(﹣3)=10℃
12-2=10℃
14-0=14℃
11-3=8℃
13-1=12℃
答:在4月1日~7日中,温差最大的是2日,3日和4的温差一样。
(4)在4月1日~7日相邻的两天中,从2日到3日温度下降最快。
【点睛】本题考查了学生动手操作能力及从统计图中获取信息的意识。
26.(1)见详解
(2)2;下降
(3)63;9;17
【分析】(1)折线统计图中横轴表示日期,纵轴表示人数,根据统计表中的数据准确描出各天对应的人数,再依次连接各点;
(2)观察折线统计图的纵轴,每格代表2人,新增确诊人数情况总体呈现下降趋势;
(3)用(20+17+8+7+6+4+1)求出这7天,共新增确诊多少人;用共新增确诊的人数除以7,求出平均每天新增确诊多少人;用8乘10,求出8天共新增确诊人数,再减去3月9日到3月15日共新增确诊人数,求出3月8日新增确诊多少人。
【详解】(1)如下图:
(2)图中每格代表2人,新增确诊人数情况总体呈现下降趋势。
(3)20+17+8+7+6+4+1
=37+15+10+1
=52+11
=63(人)
63÷7=9(人)
8×10=80(人)
80-63=17(人)
这7天,共新增确诊63人,平均每天新增确诊9人,加上3月8日新增确诊人数后,8天的平均新增确诊人数是10人,3月8日新增确诊17人。
【点睛】理解并掌握折线统计图、统计表的特点及作用,并且能够根据统计图表提供的信息解决有关实际问题是解答题目的关键。
27.①见详解
②数量;时间
③3月捐赠数量最多(答案不唯一)
④多居家运动,少聚集(答案不唯一)
【分析】①确定纵轴和横轴每一个单位的长度,数据都超过1000,起始格表示1000箱,上边每格表示100比较合适;根据各数量的多少,在方格图的纵线或横线(或纵、横的交点)上描出表示数量多少的点;把各点用线段顺次连接起来,标上数据即可。
②观察统计图,竖直方向的叫纵轴,水平方向的叫横轴,看两条轴即可确定分别表示什么。
③答案不唯一,合理即可。
④答案不唯一,合理即可。
【详解】①由分析得:
口罩厂每月捐赠红星医院口罩数量统计图
②纵轴表示数量;横轴表示时间。
③发现3月捐赠数量最多。
④答案不唯一,如多居家运动,少聚集,勤洗手等。
【点睛】折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示数量的增减变化情况。
28.(1)6月、9月、10月、11月;7月、8月
(2)11月;0.72万元
(3)0.73万元
(4)见详解(答案不唯一)
【分析】(1)实线和虚线分别表示收入和支出,当实线高于虚线时,说明收入大于支出,也就是赚钱了;相反,就是亏钱了。
(2)根据折线统计图可以知道,赚钱最多的月份是11月,再进行具体计算即可确定6月赚了多少钱。
(3)收入在图中是用实线表示,所以找到实线上的这些点所对应的金额,然后先相加再除以月份即可。
(4)根据统计图中折线的走势和实际情况分析数据产生变化的原因。
【详解】由分析可知:
(1)这辆出租车赚钱的月份有6月、9月、10月、11月,亏钱的月份有7月、8月。
(2)1.33-0.61=0.72(万元)
答:赚钱最多的月是11月,赚了0.72万元。
(3)(0.9+0.16+0.13+0.58+1.28+1.33)÷6
=4.38÷6
=0.73(万元)
答:这两车的平均收入是0.73万元。
(4)由于疫情影响,在7月和8月,人们出行量极少,因此出租车收入降到最低,从9月起,由于疫情逐渐好转,人们出行量逐渐增加,出租车的收入也就随之增加。(答案不唯一)
【点睛】本题主要考查折线统计图的实际应用,学会从统计图中找出有用的数学信息是解题关键。
29.(1) 1 6
(2) 6 120
(3)B
【分析】(1)实线表示《青铜葵花》的销售情况,虚线表示《昆虫记》的销售情况,折点越高销量越多,折点越低销量越少;
(2)两条折线之间的距离越大两种书的销量相差越大,根据图中数据求出6月两种书的销量之差;
(3)折线统计图中折线越陡销量增长越快,折线越缓销量增长越慢,据此解答。
(1)
《青铜葵花》1月销售量最少,《昆虫记》6月销售量最多。
(2)
450-330=120(册)
由图可知,《青铜葵花》和《昆虫记》销售量相差最大的是6月,相差120册。
(3)
分析可知,《昆虫记》销售量增长最快的是5月。
故答案为:B
【点睛】理解并掌握折线统计图的特点及作用,并且能够根据统计图提供的信息解决有关实际问题是解答题目的关键。
30.(1)小时
(2)小时或小时
【分析】由题意可得A、B两地相距400千米,行驶完全程甲用5小时,乙用4小时。
(1)先根据速度=路程÷时间,求出甲、乙两车速度,再用总路程除以速度和,即可得甲、乙两车出发几小时后相遇。
(2)相遇前,用总路程减120千米,再除以速度和,即可得甲车行驶多长时间后两车相距120千米;相遇后,用总路程加120千米,再除以速度和,即可得甲车行驶多长时间后两车相距120千米。
【详解】(1)400÷(400÷5+400÷4)
=400÷(80+100)
=400÷180
=(小时)
答:甲、乙两车出发小时后相遇。
(2)相遇前:
(400-120)÷(400÷5+400÷4)
=280÷180
=(小时)
相遇后:
(400+120)÷(400÷5+400÷4)
=520÷180
=(小时)
答:甲车行驶小时或小时后两车相距120千米。
【点睛】本题主要考查复式折线统计图的应用,关键根据统计图找到解决问题的信息,解决问题。
