相似三角形性质的应用[上学期]
图片预览





文档简介
课件12张PPT。相似三角形性质的应用教学目标: (1)使学生掌握相似三角形的判定定理与性质定理的综合运用 。
(2)培养学生分析解决实际问题的能力,增强学数学用数学的意识。
相似三角形的性质目目复复例1例1例2例2结练1练2板停(一)复习
1。相似三角形的判定方法有哪些?a、 b、c、d
2。相似三角形有哪些性质?a、 b、c、
3。填空(1)如果两个相似三角形周长的比是1:3,那么它们对应边的比是 (2)如果两个相似三角形的和是40,它们对应边上的中线的比是5:3,那么它们的周长分别是
(3)已知梯形两底的长分别是3.6和6,高是3,则它的两腰延长线的交点到较长的距离为 目目复复例1例1例2例2结练1练2板停(一)复习
1。相似三角形的判定方法有哪些?
2。相似三角形有哪些性质?
3。填空(1)如果两个相似三角形周长的比是1:3,那么它们对应边的比是 (2)如果两个相似三角形的和是40,它们对应边上的中线的比是5:3,那么它们的周长分别是
(3)已知梯形两底的长分别是3.6和6,高是3,则它的两腰延长线的交点到较长的距离为1:315和257.5目复复例1例1例2例2结练1练2板停分析:新授
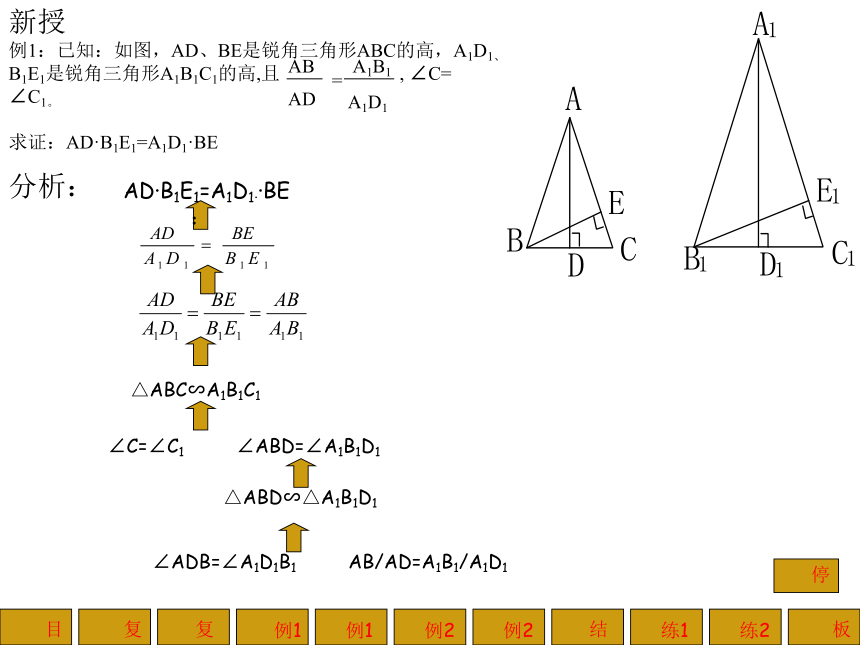
例1:已知:如图,AD、BE是锐角三角形ABC的高,A1D1、B1E1是锐角三角形A1B1C1的高,且 , ∠C=
∠C1。
求证:AD·B1E1=A1D1·BE
ABADA1B1A1D1=目复复例1例1例2例2结练1练2板AD·B1E1=A1D1··BE:△ABC∽A1B1C1∠C=∠C1 ∠ABD=∠A1B1D1△ABD∽△A1B1D1∠ADB=∠A1D1B1 AB/AD=A1B1/A1D1停
证明:∵∠ADB=∠A1D1B1= 900,
∴△ABD∽△A1B1D1
∴ ∠ABD=∠ A1B1D1
∵∠C=∠C1
∴△ABC=△A1B1C1
∴
∴AD·B1E1=A1D1·BEABA1B1=ADA1D1=BEB1E1(相似三角形对应高的比等于相似
比)目复复例1例1例2例2结练1练2板停例2:如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
分析:四边形PQMN是正方形PN∥QM,PN=QM,QM在BC边上(已知)PN∥BC△APN∽△ABC
C目复复例1例1例2例2结练1练2板停解:设正方形的边长为y毫米,则AE为(80—y)毫米
∵PN∥BC
∴△APN∽△ABC
∴即解得:y=48毫米目复复例1例1例2例2结练1练2板停课结: (1)在解题的过程中学会灵活运用相似三角形的
判定及性质的综和运用。
(2)关于几何的记算问题,常用到设未知量为y,从而转化
为代数中方程求解问题。
(3)几何记算题,一定先要有推理,再列出方程。目复复例1例1例2例2结练1练2板停练习巩固:
1,设AD、BE和CF是锐角三角形ABC的三条高。
求证:AD×BC=BE×CA=CF×AB要证AD×BC=BE×CA=CF×AB证明: 略目复复例1例1例2例2结练1练2板AD·BC=BE·CA AD·BC=CF·AB△ADC∽△BEC∠ADC=∠BEC=900 ∠C=∠C分析:△ABD∽△BCF∠B=∠B ∠ADB=∠BFC停练习: (2)当把例2中的三角形余料,加工成矩形,且PN=2PQ时,PN是多少?解:如图设PQ为 y 毫米,则PN为 2 y 毫米,AE为(80-y )毫米。
∵PN∥BC
∴△APN∽△ABC
∴
∴
y
AEADPNBC=(相似三角形对应高
的比等于相似比)80-y80=2y1202407(毫米)=目复复例1例1例2例2结练1练2板停
1。 平行于三角形一边的直线和其它两边(或两边
的延长线)相交,所构成的时间三角形与原三角形相似)
2。 相似三角形对应高的比等于相似比。例1 例2作业: P247 6 、 7目复复例1例1例2例2结练1练2板停板书设计
(2)培养学生分析解决实际问题的能力,增强学数学用数学的意识。
相似三角形的性质目目复复例1例1例2例2结练1练2板停(一)复习
1。相似三角形的判定方法有哪些?a、 b、c、d
2。相似三角形有哪些性质?a、 b、c、
3。填空(1)如果两个相似三角形周长的比是1:3,那么它们对应边的比是 (2)如果两个相似三角形的和是40,它们对应边上的中线的比是5:3,那么它们的周长分别是
(3)已知梯形两底的长分别是3.6和6,高是3,则它的两腰延长线的交点到较长的距离为 目目复复例1例1例2例2结练1练2板停(一)复习
1。相似三角形的判定方法有哪些?
2。相似三角形有哪些性质?
3。填空(1)如果两个相似三角形周长的比是1:3,那么它们对应边的比是 (2)如果两个相似三角形的和是40,它们对应边上的中线的比是5:3,那么它们的周长分别是
(3)已知梯形两底的长分别是3.6和6,高是3,则它的两腰延长线的交点到较长的距离为1:315和257.5目复复例1例1例2例2结练1练2板停分析:新授
例1:已知:如图,AD、BE是锐角三角形ABC的高,A1D1、B1E1是锐角三角形A1B1C1的高,且 , ∠C=
∠C1。
求证:AD·B1E1=A1D1·BE
ABADA1B1A1D1=目复复例1例1例2例2结练1练2板AD·B1E1=A1D1··BE:△ABC∽A1B1C1∠C=∠C1 ∠ABD=∠A1B1D1△ABD∽△A1B1D1∠ADB=∠A1D1B1 AB/AD=A1B1/A1D1停
证明:∵∠ADB=∠A1D1B1= 900,
∴△ABD∽△A1B1D1
∴ ∠ABD=∠ A1B1D1
∵∠C=∠C1
∴△ABC=△A1B1C1
∴
∴AD·B1E1=A1D1·BEABA1B1=ADA1D1=BEB1E1(相似三角形对应高的比等于相似
比)目复复例1例1例2例2结练1练2板停例2:如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
分析:四边形PQMN是正方形PN∥QM,PN=QM,QM在BC边上(已知)PN∥BC△APN∽△ABC
C目复复例1例1例2例2结练1练2板停解:设正方形的边长为y毫米,则AE为(80—y)毫米
∵PN∥BC
∴△APN∽△ABC
∴即解得:y=48毫米目复复例1例1例2例2结练1练2板停课结: (1)在解题的过程中学会灵活运用相似三角形的
判定及性质的综和运用。
(2)关于几何的记算问题,常用到设未知量为y,从而转化
为代数中方程求解问题。
(3)几何记算题,一定先要有推理,再列出方程。目复复例1例1例2例2结练1练2板停练习巩固:
1,设AD、BE和CF是锐角三角形ABC的三条高。
求证:AD×BC=BE×CA=CF×AB要证AD×BC=BE×CA=CF×AB证明: 略目复复例1例1例2例2结练1练2板AD·BC=BE·CA AD·BC=CF·AB△ADC∽△BEC∠ADC=∠BEC=900 ∠C=∠C分析:△ABD∽△BCF∠B=∠B ∠ADB=∠BFC停练习: (2)当把例2中的三角形余料,加工成矩形,且PN=2PQ时,PN是多少?解:如图设PQ为 y 毫米,则PN为 2 y 毫米,AE为(80-y )毫米。
∵PN∥BC
∴△APN∽△ABC
∴
∴
y
AEADPNBC=(相似三角形对应高
的比等于相似比)80-y80=2y1202407(毫米)=目复复例1例1例2例2结练1练2板停
1。 平行于三角形一边的直线和其它两边(或两边
的延长线)相交,所构成的时间三角形与原三角形相似)
2。 相似三角形对应高的比等于相似比。例1 例2作业: P247 6 、 7目复复例1例1例2例2结练1练2板停板书设计
