3.3-相似三角形性质与判定(2)[上学期]
文档属性
| 名称 | 3.3-相似三角形性质与判定(2)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 86.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-02 00:00:00 | ||
图片预览

文档简介
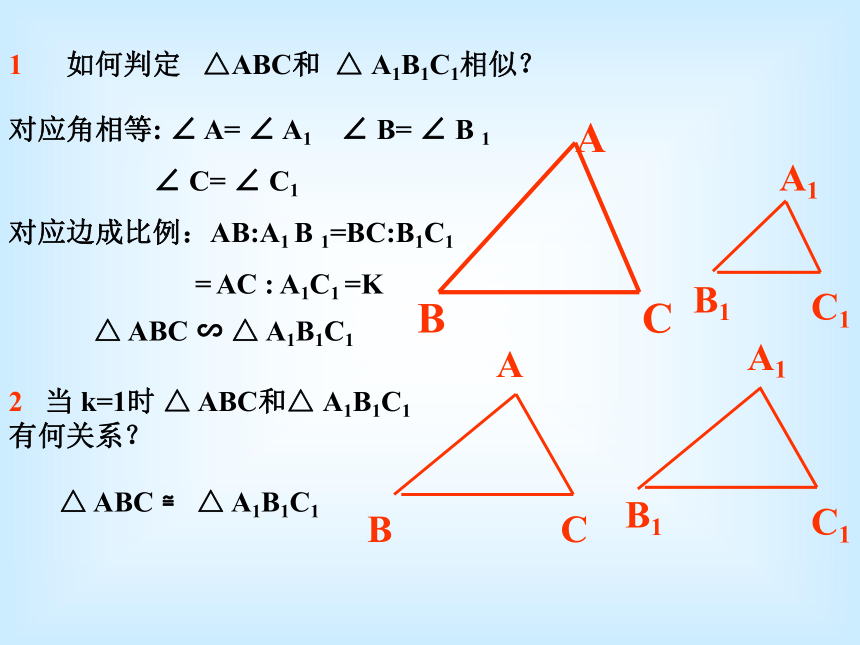
课件11张PPT。3.3 相似三角形的性质和判定(2)1 如何判定 △ABC和 △ A1B1C1相似?对应角相等: ∠ A= ∠ A1 ∠ B= ∠ B 1
∠ C= ∠ C1
对应边成比例:AB:A1 B 1=BC:B1C1
= AC : A1C1 =K2 当 k=1时 △ ABC和△ A1B1C1有何关系? △ ABC ≌ △ A1B1C1A1B1C1△ ABC ∽ △ A1B1C1有两个角对应相等的两个三角形相似已知:如图 ∠A=∠A 1 ∠B=∠B1
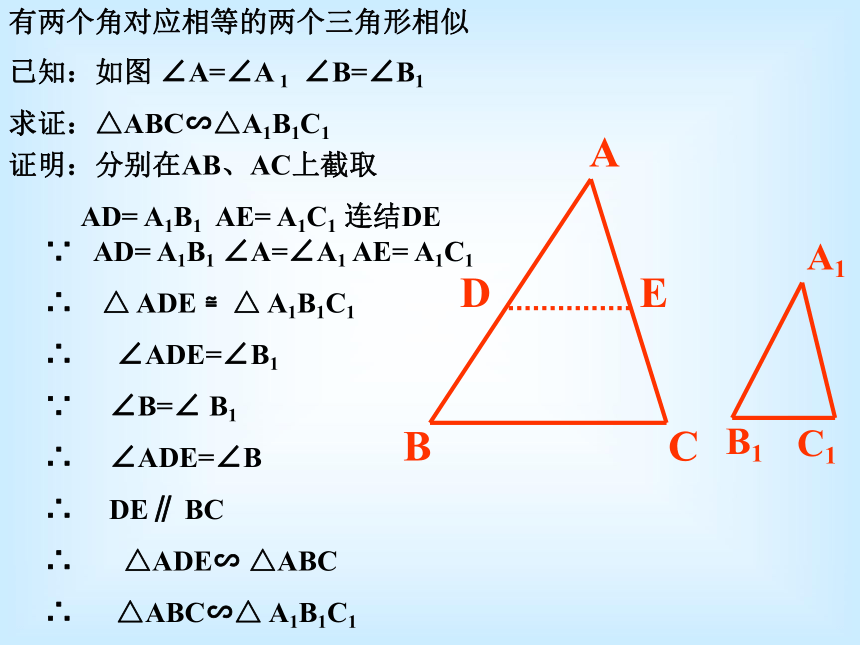
求证:△ABC∽△A1B1C1证明:分别在AB、AC上截取
AD= A1B1 AE= A1C1 连结DE ∵ AD= A1B1 ∠A=∠A1 AE= A1C1
∴ △ ADE ≌△ A1B1C1
∴ ∠ADE=∠B1
∵ ∠B=∠ B1
∴ ∠ADE=∠B
∴ DE∥ BC
∴ △ADE∽ △ABC
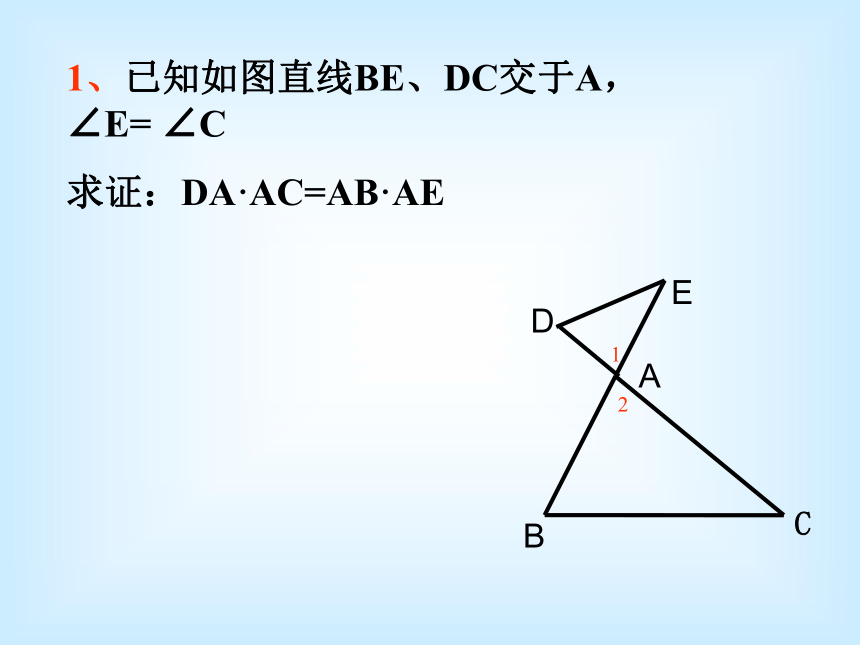
∴ △ABC∽△ A1B1C1 1、已知如图直线BE、DC交于A, ∠E= ∠C
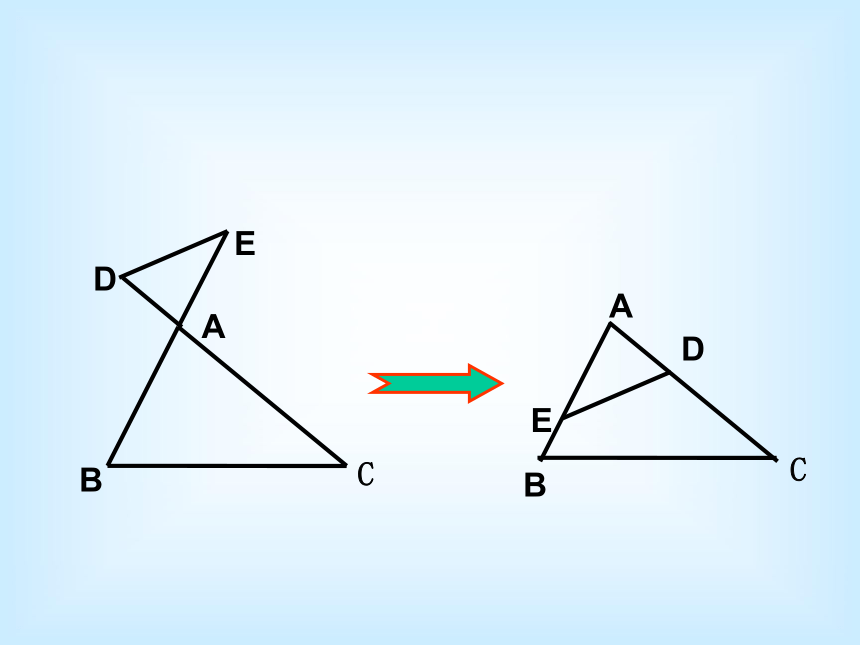
求证:DA·AC=AB·AEDEABC12EABDC解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4已知如图, ∠ABD=∠C AD=2 AC=8,求AB ABDC3、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
问:①图中有几个直角三角形?它们相似吗?为什么?解: 图中有三个直角三角形,分别是: △ ABC、 △ ADB、 △ BDC
△ ABC ∽ △ ADB ∽ △ BDC
DBC3、如图:在Rt △ ABC中 , ∠ABC=90° BD⊥AC于D
② 求证:AB2=AD · AC BD2=AD · DCA 如图,△ABC∽△A′B′C′,相似比为k,分别作BC , B′C′上的高AD和A′D′.求证:相似三角形性质:相似三角形面积的比等于相似比的平方总结:
1、化归思想,将未知问题转化为已知问题
2、相似三角形的判定一:有两个角相等的两个三角形相似
3、直角三角形被斜边上的高分成的两个直角三角形和原三角形 相似
∵ ∠BAC= 900,BD⊥AC
∴ △ABC ∽ △DBA ∽ △DAC
4、证明线段的乘积问题可转化为线段的比例问题
5、相似三角形面积的比等于相似比的平方ABDC
∠ C= ∠ C1
对应边成比例:AB:A1 B 1=BC:B1C1
= AC : A1C1 =K2 当 k=1时 △ ABC和△ A1B1C1有何关系? △ ABC ≌ △ A1B1C1A1B1C1△ ABC ∽ △ A1B1C1有两个角对应相等的两个三角形相似已知:如图 ∠A=∠A 1 ∠B=∠B1
求证:△ABC∽△A1B1C1证明:分别在AB、AC上截取
AD= A1B1 AE= A1C1 连结DE ∵ AD= A1B1 ∠A=∠A1 AE= A1C1
∴ △ ADE ≌△ A1B1C1
∴ ∠ADE=∠B1
∵ ∠B=∠ B1
∴ ∠ADE=∠B
∴ DE∥ BC
∴ △ADE∽ △ABC
∴ △ABC∽△ A1B1C1 1、已知如图直线BE、DC交于A, ∠E= ∠C
求证:DA·AC=AB·AEDEABC12EABDC解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4已知如图, ∠ABD=∠C AD=2 AC=8,求AB ABDC3、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D
问:①图中有几个直角三角形?它们相似吗?为什么?解: 图中有三个直角三角形,分别是: △ ABC、 △ ADB、 △ BDC
△ ABC ∽ △ ADB ∽ △ BDC
DBC3、如图:在Rt △ ABC中 , ∠ABC=90° BD⊥AC于D
② 求证:AB2=AD · AC BD2=AD · DCA 如图,△ABC∽△A′B′C′,相似比为k,分别作BC , B′C′上的高AD和A′D′.求证:相似三角形性质:相似三角形面积的比等于相似比的平方总结:
1、化归思想,将未知问题转化为已知问题
2、相似三角形的判定一:有两个角相等的两个三角形相似
3、直角三角形被斜边上的高分成的两个直角三角形和原三角形 相似
∵ ∠BAC= 900,BD⊥AC
∴ △ABC ∽ △DBA ∽ △DAC
4、证明线段的乘积问题可转化为线段的比例问题
5、相似三角形面积的比等于相似比的平方ABDC
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
