3.3-相似三角形性质与判定(3)[上学期]
文档属性
| 名称 | 3.3-相似三角形性质与判定(3)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 684.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-09 00:00:00 | ||
图片预览



文档简介
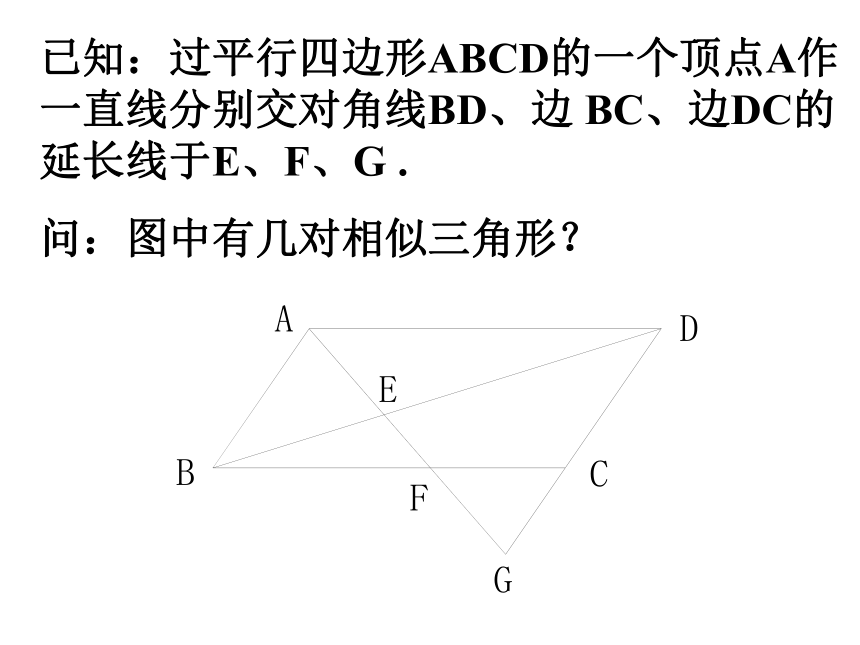
课件15张PPT。义务教育课程标准实验教科书九年级 上册湖南教育出版社3.3 相似三角形的性质和判定(3)相似三角形的判定方法有那些?方法1:定义方法2:三边对应成比例。复习方法3:两角对应相等。已知:过平行四边形ABCD的一个顶点A作一直线分别交对角线BD、边 BC、边DC的延长线于E、F、G .
问:图中有几对相似三角形?画△ABC与△A′B′C′,使∠A= ∠A′,且
把相似比2换成任意一个正数k,
△A′B′C ′与 △ABC相似吗?
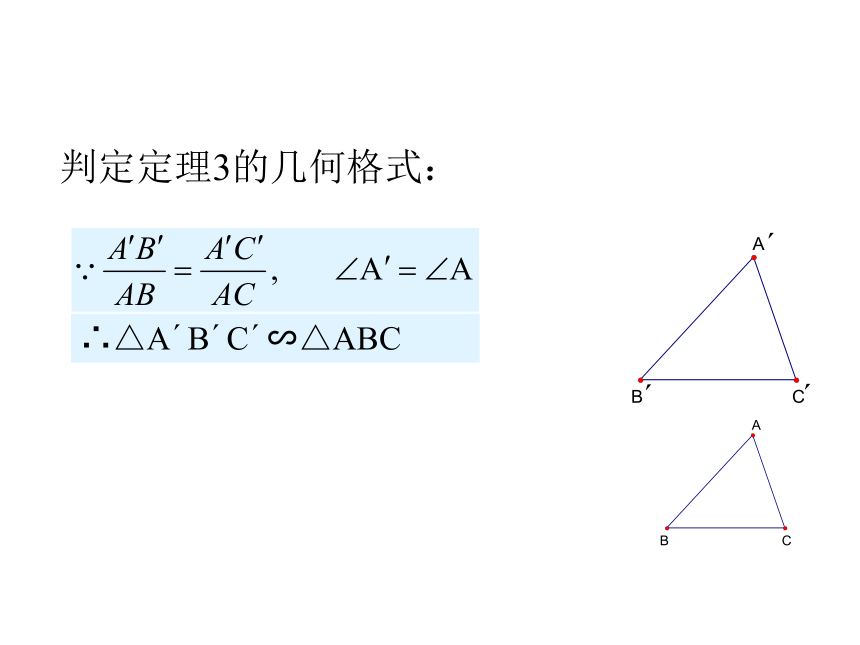
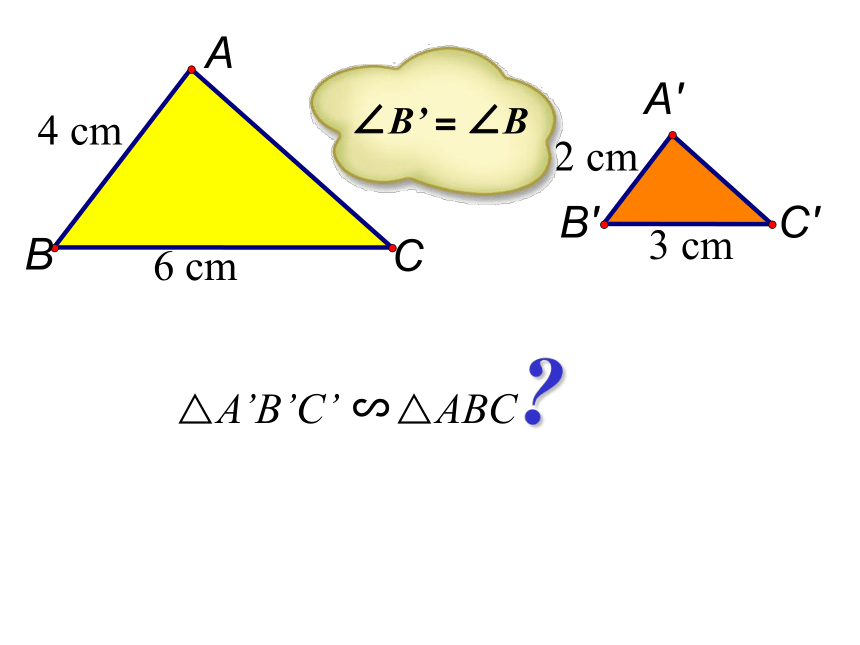
△A′B′C ′与 △ABC相似吗?探究可以证明下述定理: 判定定理3 如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简单说成: 两条直角边对应成比例的两个直角三角形相似吗?为什么?两条边对应成比例且夹角相等的两个三角形相似.判定定理3的几何格式:∴△A′B′C′∽△ABC6 cm4 cm3 cm2 cm△A’B’C’ ∽△ABC?∠B’=∠B判断下图中△AEB和△FEC是否相似? 解 ∵∠AEB=∠FEC(对应角相等)
?
又∵ = =1.5
?
= =1.5
?
∴ =
?
∴ △AEB∽△FEC 例1 如图,在△ABC与△DEF中,∠B=∠E=40°,AB=4.2cm,
AC=3cm,DE=2.1cm,DF=1.5cm. △ ABC 与△DEF有两边对
应成比例吗?有一个角对应相等吗?这两个三角形相似吗?从上述例子你能得出什么结论?观察例2如图,在Rt△ABC与Rt△A′B′C′中,
∠C=∠C ′=90°,且求证:△A′B′C ′∽△ABC相似吗?1.已知在Rt△ABC与Rt△A′B′C′中,∠C=∠C ′=90°,
AC=3cm,BC=2cm, A′C ′= 4.2cm, B′C ′=2.8cm.
求证: △ABC∽△A′B′C′.2.已知在Rt△ABC与Rt△A′B′C′中,∠C=∠C ′=90°,
AB=6cm,AC=4.8cm, A′B ′= 5cm, B′C ′=3cm.
求证: △ABC∽△A′B′C′.练习如图,D在⊿ABC的AB边上,AD=1,BD=2,
AC= ,问⊿ ACD与⊿ ABC相似吗?
请说明你的理由.想一想小结两个三角形相似的判定方法:(1) 三角形相似的定义.(2) 三边对应成比例的两个三角形相似.(3) 两角对应相等的两个三角形相似.(4) 两边对应成比例且夹角相等的两个三角形相似.看已知条件判定相似选择方法找出识别方法中所需的条件1.本子:P80-5、6
2.培优:P43-44 作业
问:图中有几对相似三角形?画△ABC与△A′B′C′,使∠A= ∠A′,且
把相似比2换成任意一个正数k,
△A′B′C ′与 △ABC相似吗?
△A′B′C ′与 △ABC相似吗?探究可以证明下述定理: 判定定理3 如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.简单说成: 两条直角边对应成比例的两个直角三角形相似吗?为什么?两条边对应成比例且夹角相等的两个三角形相似.判定定理3的几何格式:∴△A′B′C′∽△ABC6 cm4 cm3 cm2 cm△A’B’C’ ∽△ABC?∠B’=∠B判断下图中△AEB和△FEC是否相似? 解 ∵∠AEB=∠FEC(对应角相等)
?
又∵ = =1.5
?
= =1.5
?
∴ =
?
∴ △AEB∽△FEC 例1 如图,在△ABC与△DEF中,∠B=∠E=40°,AB=4.2cm,
AC=3cm,DE=2.1cm,DF=1.5cm. △ ABC 与△DEF有两边对
应成比例吗?有一个角对应相等吗?这两个三角形相似吗?从上述例子你能得出什么结论?观察例2如图,在Rt△ABC与Rt△A′B′C′中,
∠C=∠C ′=90°,且求证:△A′B′C ′∽△ABC相似吗?1.已知在Rt△ABC与Rt△A′B′C′中,∠C=∠C ′=90°,
AC=3cm,BC=2cm, A′C ′= 4.2cm, B′C ′=2.8cm.
求证: △ABC∽△A′B′C′.2.已知在Rt△ABC与Rt△A′B′C′中,∠C=∠C ′=90°,
AB=6cm,AC=4.8cm, A′B ′= 5cm, B′C ′=3cm.
求证: △ABC∽△A′B′C′.练习如图,D在⊿ABC的AB边上,AD=1,BD=2,
AC= ,问⊿ ACD与⊿ ABC相似吗?
请说明你的理由.想一想小结两个三角形相似的判定方法:(1) 三角形相似的定义.(2) 三边对应成比例的两个三角形相似.(3) 两角对应相等的两个三角形相似.(4) 两边对应成比例且夹角相等的两个三角形相似.看已知条件判定相似选择方法找出识别方法中所需的条件1.本子:P80-5、6
2.培优:P43-44 作业
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
