人教版 七年级下册第七章 平面直角坐标系 单元综合练习(含解析)
文档属性
| 名称 | 人教版 七年级下册第七章 平面直角坐标系 单元综合练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 645.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 07:28:01 | ||
图片预览




文档简介
第七章 平面直角坐标系 单元综合练习
一、单选题
1.下列图形中,∠1与∠2是对顶角的是( )
A. B. C. D.
2.在下列所给出坐标的点中,在第二象限的是
A.(2,3) B.(﹣2,3) C.(﹣2,﹣3) D.(2,﹣3)
3.平面直角坐标系中有一点P,点P到y轴的距离为2,点P的纵坐标为﹣3,则点P的坐标是( )
A.(﹣3,﹣2) B.(﹣2,﹣3) C.(2,﹣3) D.(2,﹣3)或(﹣2,﹣3)
4.在平面直角坐标系中,将点向左平移2个单位长度后得到的点的坐标是( )
A. B. C. D.
5.课间操时,小华、小军、小刚的位置如图.小华对小刚说:“如果我的位置用表示,小军的位置用表示,那么你的位置可以表示成( )
A. B. C. D.
6.点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P坐标是( )
A.(3, 3) B.(3,-3) C.(6,-6) D.(3,3)或
7.下列不能准确表示地理位置的是( )
A.东经度,北纬度 B.方向南偏东,距离公里
C.距三明北动车站 D.排号
8. 已知点P(0,m)在y轴的负半轴上,则点M( m, m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.在平面直角坐标系中,已知线段AB的两个端点分别是A(4,-1),B(1,1)将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为( )
A.(-5,4)
B.(4,3)
C.(-1,-2)
D.(-2,-1)
10.已知点,若直线轴,点P在x轴的负半轴上,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.如图,在平面直角坐标系中,点C,D分别是,的中点,点A的坐标为,点D的坐标为,则点C的坐标为( )
A. B. C. D.
12.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是( )
A.(66,34) B.(67,33) C.(100,33) D.(99,34)
13.甲、乙、丙三人所处的位置不同,甲说:“以我为坐标原点,乙的位置是,”丙说:“以我为坐标原点,乙的位置是.”则以乙为坐标原点,甲、丙的坐标分别是(已知三人所建立的直角坐标系在同一平面内,且x轴、y轴的正方向相同)( )
A., B.,
C., D.,
14.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是( )
A.点A B.点B C.点C D.点D
15.已知点E(x0,y0),F(x2,y2),点M(x1,y1)是线段EF的中点,则,.在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1(即P,A,P1三点共线,且PA=P1A),P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称点重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是( )
A.(0,0) B.(0,2)
C.(2,-4) D.(-4,2)
二、填空题
16.点的坐标为,则点到轴的距离为______.
17.直线分别交x轴,y轴于两点,点O为坐标原点,且,则a的值是_______.
18.如图,线段AB两端点的坐标分别为A(﹣1,0),B(1,1),把线段AB平移到CD位置,若线段CD两端点的坐标分别为C(1,a),D(b,4),则a+b的值为_____
19.如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(﹣3,4)的对应点是A1(2,5),则点B(﹣4,2)的对应点B1的坐标是________.
20.如图,在平面直角坐标系中,一动点从原点O出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2016的坐标为________.
三、解答题
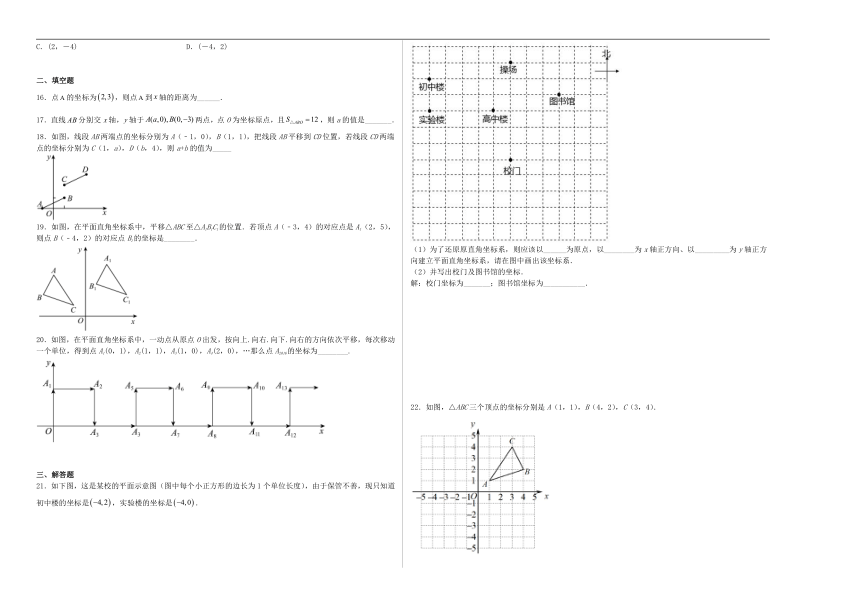
21.如下图,这是某校的平面示意图(图中每个小正方形的边长为1个单位长度),由于保管不善,现只知道初中楼的坐标是,实验楼的坐标是.
(1)为了还原原直角坐标系,则应该以______为原点,以________为x轴正方向、以_________为y轴正方向建立平面直角坐标系,请在图中画出该坐标系.
(2)并写出校门及图书馆的坐标.
解:校门坐标为_______;图书馆坐标为___________.
22.如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于x轴对称的图形△;
(2)求△ABC的面积;
(3)在x轴上求一点P,使△PAB周长最小,请画出△PAB,并通过画图求出P点的坐标.
23.如图,在平面直角坐标系中,,,将线段平移后得线段,其中B的对应点的坐标是.
(1)在图中画出线段和;
(2)直接写出线段上一点经过平移后的对应点的坐标.
24.已知平面直角坐标系中,点P的坐标为
(1)当m为何值时,点P到x轴的距离为1
(2)当m为何值时,点P到y轴的距离为2?
(3)点P可能在第一象限坐标轴夹角的平分线上吗?若可能,求出m的值;若不可能,请说明理由.
25.如图是某台阶的一部分,如果A点的坐标为(0,0),B点的坐标为(1,1),
(1)请建立适当的直角坐标系,并写出其余各点的坐标;
(2)如果台阶有10级,请你求出该台阶的长度和高度;
(3)若这10级台阶的宽度都是2m,单位长度为1m,现要将这些台阶铺上地毯,需要多少平方米?
参考答案
1.C
【详解】解:A、∠1与∠2不是对顶角,故此选项错误;
B、∠1与∠2不是对顶角,故此选项错误;
C、∠1与∠2是对顶角,故此选项正确;
D、∠1与∠2不是对顶角,故此选项错误;
故选:C.
2.B
【详解】解:∵第二象限内点的横坐标是负数,纵坐标是正数,
∴(2,3)、(-2,3)、(-2,-3)、(2,-3)中只有(-2,3)在第二象限.
故选:B.
3.D
【详解】∵点P到y轴的距离为2,
∴点P的横坐标为,
又点P的纵坐标为﹣3,
∴点P的坐标是(2,﹣3)或(﹣2,﹣3)
4.A
【详解】解:将点向左平移2个单位长度得到的点坐标为,
故选A.
5.D
【详解】解:由如果小华的位置用表示,小军的位置用表示可知:小刚的位置可以表示为
故选D.
6.D
【详解】解: 点P到两坐标轴的距离相等,
或
当时,
当
综上:的坐标为:或
故选D.
7.C
【详解】解:A.东经度,北纬度,能准确表示地理位置,不合题意;
B.方向南偏东,距离公里,能准确表示地理位置,不合题意;
C.距三明北动车站,不能准确表示地理位置,符合题意;
D.排号,能准确表示地理位置,不合题意;
故选:C.
8.A
【详解】点P(0,m)在y轴的负半轴上,
∴m<0,
∴-m>0,-m+1>0,
∴点M(-m,-m+1)在第一象限;
故选:A
9.A
【详解】∵点A(4,﹣1)向左平移6个单位,再向上平移3个单位得到A′(﹣2,2),
∴点B(1,1)向左平移6个单位,再向上平移3个单位得到的对应点B′的坐标为(﹣5,4).
故选A.
10.C
【详解】解:∵直线ABx轴,
∴2a+2=4,解得:a=1,
∵点P在x轴的负半轴上,
∴b<0,
∴b-a=b-1<0,a-2=1-2=-1<0,
.点M在第三象限.
故选:C.
11.A
【详解】解:设B(x,y),
∵D为OB的中点,且O(0,0)
∴
∴
∴B(2,4)
设点C的坐标为(m,n)
∵A
∴
∴C(4,2)
故选A
12.C
【详解】试题分析:由题意得,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,
∵100÷3=33余1,
∴走完第100步,为第34个循环组的第1步,
所处位置的横坐标为33×3+1=100,
纵坐标为33×1=33,
∴棋子所处位置的坐标是(100,33).
故选C.
13.C
【详解】∵以甲为坐标原点,乙的位置是,
∴以乙为坐标原点,甲的位置是;
∵以丙为坐标原点,乙的位置是,
∴以乙为坐标原点,丙的位置是.
故选C.
14.B
【详解】由题意知(10,20)表示向东走10米,再向北走20米,故为B点.
故选:B.
15.A
【详解】设P1(x,y),
∵点A(1,-1)、B(-1,-1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,
∴=1,=-1,解得x=2,y=-4,
∴P1(2,-4).
同理可得,P1(2,-4),P2(-4,2),P3(4,0),P4(-2,-2),P5(0,0),P6(0,2),P7(2,-4),…,…,
∴每6个数循环一次.
∵=335…5,
∴点P2015的坐标是(0,0).
故选A.
16.3
【详解】解:点的坐标为,则点到轴的距离为3.
故答案为:3.
17.
【详解】∵直线分别交x轴,y轴于两点,,
∴OB=3,,
解得:OA=8,
∴=8,
解得:a=,
故答案为:
18.6
【详解】解:点A的横坐标为-1,点C的横坐标为1,
则线段AB先向右平移2个单位,
∵点B的横坐标为1,
∴点D的横坐标为3,即b=3,
点B的纵坐标为1,点D的纵坐标为4,
则线段AB向上平移3个单位,
∵点A的纵坐标为0,
∴点C的纵坐标为3,即a=3,
∴a+b=3+3=6,
故答案为:6.
19.(1,3)
【详解】解:∵顶点A(﹣3,4)的对应点是A1(2,5),
又
∴平移至的规律为:将向右平移5个单位,再向上平移1个单位即可得到
∵B(﹣4,2)
∴的坐标是(-4+5,2+1),即(1,3)
故答案为:(1,3)
20.(1008,0)
【详解】解:由图可知,4个点为一个循环组依次循环,
∵2016÷4=504,
∴点A2016是第504循环组的最后一个点,
504×2=1008,
∴点A2016的坐标为(1008,0).
故答案为(1008,0).
21.(1)高中楼,正东方向,正北方向,(2),;
【详解】(1)根据初中楼的坐标是,实验楼的坐标是,建立平面直角坐标系如图所示:
故答案为:高中楼,正东方向,正北方向;
(2)由(1)建立的直角坐标系得,
校门坐标(1,-3),图书馆坐标(4,1),
故答案为:,.
22.(1)图见详解
(2)
(3)图见详解,点的坐标为
【详解】(1)解:如图,△即为所求.
(2)解:由图可得:
.
的面积为.
(3)解:如图,即为所求.
由图可知点的坐标为.
23.(1)见解析
(2)
【详解】(1)解:如图:线段和即为所求.
(2)解:∵平移后得到
∴平移方式为“向下平移一个单位长度,向左平移3个单位长度”
∵
∴.
24.(1), ;(2),;(3)不可能,理由见解析.
【详解】解:点P到x轴的距离为1,,
点P到y轴的距离为2,,
如果点P可能在第一象限坐标轴夹角的平分线上点P在第一象限
,,不合题意
点P不可能在第一象限坐标轴夹角的平分线上.
25.(1)建立平面直角坐标系见解析,C(2,2),D(3,3),E(4,4),F(5,5);(2)11;10;(3)需要42平方米.
【详解】(1)建立平面直角坐标系如图所示,
C(2,2),D(3,3),E(4,4),F(5,5);
(2)台阶的长度:1×(10+1)=11,
高度:1×10=10;
(3)∵单位长度为1m,
∴地毯的长度为:(11+10)×1=21m,
∵台阶的宽度都是2m,
∴地毯的面积为21×2=42m2,
答:将这些台阶铺上地毯,需要42平方米.
一、单选题
1.下列图形中,∠1与∠2是对顶角的是( )
A. B. C. D.
2.在下列所给出坐标的点中,在第二象限的是
A.(2,3) B.(﹣2,3) C.(﹣2,﹣3) D.(2,﹣3)
3.平面直角坐标系中有一点P,点P到y轴的距离为2,点P的纵坐标为﹣3,则点P的坐标是( )
A.(﹣3,﹣2) B.(﹣2,﹣3) C.(2,﹣3) D.(2,﹣3)或(﹣2,﹣3)
4.在平面直角坐标系中,将点向左平移2个单位长度后得到的点的坐标是( )
A. B. C. D.
5.课间操时,小华、小军、小刚的位置如图.小华对小刚说:“如果我的位置用表示,小军的位置用表示,那么你的位置可以表示成( )
A. B. C. D.
6.点P的坐标是(2-a,3a+6),且点P到两坐标轴的距离相等,则点P坐标是( )
A.(3, 3) B.(3,-3) C.(6,-6) D.(3,3)或
7.下列不能准确表示地理位置的是( )
A.东经度,北纬度 B.方向南偏东,距离公里
C.距三明北动车站 D.排号
8. 已知点P(0,m)在y轴的负半轴上,则点M( m, m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.在平面直角坐标系中,已知线段AB的两个端点分别是A(4,-1),B(1,1)将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2),则点B′的坐标为( )
A.(-5,4)
B.(4,3)
C.(-1,-2)
D.(-2,-1)
10.已知点,若直线轴,点P在x轴的负半轴上,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.如图,在平面直角坐标系中,点C,D分别是,的中点,点A的坐标为,点D的坐标为,则点C的坐标为( )
A. B. C. D.
12.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是( )
A.(66,34) B.(67,33) C.(100,33) D.(99,34)
13.甲、乙、丙三人所处的位置不同,甲说:“以我为坐标原点,乙的位置是,”丙说:“以我为坐标原点,乙的位置是.”则以乙为坐标原点,甲、丙的坐标分别是(已知三人所建立的直角坐标系在同一平面内,且x轴、y轴的正方向相同)( )
A., B.,
C., D.,
14.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是( )
A.点A B.点B C.点C D.点D
15.已知点E(x0,y0),F(x2,y2),点M(x1,y1)是线段EF的中点,则,.在平面直角坐标系中有三个点A(1,-1),B(-1,-1),C(0,1),点P(0,2)关于A的对称点为P1(即P,A,P1三点共线,且PA=P1A),P1关于B的对称点为P2,P2关于C的对称点为P3,按此规律继续以A,B,C为对称点重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是( )
A.(0,0) B.(0,2)
C.(2,-4) D.(-4,2)
二、填空题
16.点的坐标为,则点到轴的距离为______.
17.直线分别交x轴,y轴于两点,点O为坐标原点,且,则a的值是_______.
18.如图,线段AB两端点的坐标分别为A(﹣1,0),B(1,1),把线段AB平移到CD位置,若线段CD两端点的坐标分别为C(1,a),D(b,4),则a+b的值为_____
19.如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(﹣3,4)的对应点是A1(2,5),则点B(﹣4,2)的对应点B1的坐标是________.
20.如图,在平面直角坐标系中,一动点从原点O出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2016的坐标为________.
三、解答题
21.如下图,这是某校的平面示意图(图中每个小正方形的边长为1个单位长度),由于保管不善,现只知道初中楼的坐标是,实验楼的坐标是.
(1)为了还原原直角坐标系,则应该以______为原点,以________为x轴正方向、以_________为y轴正方向建立平面直角坐标系,请在图中画出该坐标系.
(2)并写出校门及图书馆的坐标.
解:校门坐标为_______;图书馆坐标为___________.
22.如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于x轴对称的图形△;
(2)求△ABC的面积;
(3)在x轴上求一点P,使△PAB周长最小,请画出△PAB,并通过画图求出P点的坐标.
23.如图,在平面直角坐标系中,,,将线段平移后得线段,其中B的对应点的坐标是.
(1)在图中画出线段和;
(2)直接写出线段上一点经过平移后的对应点的坐标.
24.已知平面直角坐标系中,点P的坐标为
(1)当m为何值时,点P到x轴的距离为1
(2)当m为何值时,点P到y轴的距离为2?
(3)点P可能在第一象限坐标轴夹角的平分线上吗?若可能,求出m的值;若不可能,请说明理由.
25.如图是某台阶的一部分,如果A点的坐标为(0,0),B点的坐标为(1,1),
(1)请建立适当的直角坐标系,并写出其余各点的坐标;
(2)如果台阶有10级,请你求出该台阶的长度和高度;
(3)若这10级台阶的宽度都是2m,单位长度为1m,现要将这些台阶铺上地毯,需要多少平方米?
参考答案
1.C
【详解】解:A、∠1与∠2不是对顶角,故此选项错误;
B、∠1与∠2不是对顶角,故此选项错误;
C、∠1与∠2是对顶角,故此选项正确;
D、∠1与∠2不是对顶角,故此选项错误;
故选:C.
2.B
【详解】解:∵第二象限内点的横坐标是负数,纵坐标是正数,
∴(2,3)、(-2,3)、(-2,-3)、(2,-3)中只有(-2,3)在第二象限.
故选:B.
3.D
【详解】∵点P到y轴的距离为2,
∴点P的横坐标为,
又点P的纵坐标为﹣3,
∴点P的坐标是(2,﹣3)或(﹣2,﹣3)
4.A
【详解】解:将点向左平移2个单位长度得到的点坐标为,
故选A.
5.D
【详解】解:由如果小华的位置用表示,小军的位置用表示可知:小刚的位置可以表示为
故选D.
6.D
【详解】解: 点P到两坐标轴的距离相等,
或
当时,
当
综上:的坐标为:或
故选D.
7.C
【详解】解:A.东经度,北纬度,能准确表示地理位置,不合题意;
B.方向南偏东,距离公里,能准确表示地理位置,不合题意;
C.距三明北动车站,不能准确表示地理位置,符合题意;
D.排号,能准确表示地理位置,不合题意;
故选:C.
8.A
【详解】点P(0,m)在y轴的负半轴上,
∴m<0,
∴-m>0,-m+1>0,
∴点M(-m,-m+1)在第一象限;
故选:A
9.A
【详解】∵点A(4,﹣1)向左平移6个单位,再向上平移3个单位得到A′(﹣2,2),
∴点B(1,1)向左平移6个单位,再向上平移3个单位得到的对应点B′的坐标为(﹣5,4).
故选A.
10.C
【详解】解:∵直线ABx轴,
∴2a+2=4,解得:a=1,
∵点P在x轴的负半轴上,
∴b<0,
∴b-a=b-1<0,a-2=1-2=-1<0,
.点M在第三象限.
故选:C.
11.A
【详解】解:设B(x,y),
∵D为OB的中点,且O(0,0)
∴
∴
∴B(2,4)
设点C的坐标为(m,n)
∵A
∴
∴C(4,2)
故选A
12.C
【详解】试题分析:由题意得,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,
∵100÷3=33余1,
∴走完第100步,为第34个循环组的第1步,
所处位置的横坐标为33×3+1=100,
纵坐标为33×1=33,
∴棋子所处位置的坐标是(100,33).
故选C.
13.C
【详解】∵以甲为坐标原点,乙的位置是,
∴以乙为坐标原点,甲的位置是;
∵以丙为坐标原点,乙的位置是,
∴以乙为坐标原点,丙的位置是.
故选C.
14.B
【详解】由题意知(10,20)表示向东走10米,再向北走20米,故为B点.
故选:B.
15.A
【详解】设P1(x,y),
∵点A(1,-1)、B(-1,-1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,
∴=1,=-1,解得x=2,y=-4,
∴P1(2,-4).
同理可得,P1(2,-4),P2(-4,2),P3(4,0),P4(-2,-2),P5(0,0),P6(0,2),P7(2,-4),…,…,
∴每6个数循环一次.
∵=335…5,
∴点P2015的坐标是(0,0).
故选A.
16.3
【详解】解:点的坐标为,则点到轴的距离为3.
故答案为:3.
17.
【详解】∵直线分别交x轴,y轴于两点,,
∴OB=3,,
解得:OA=8,
∴=8,
解得:a=,
故答案为:
18.6
【详解】解:点A的横坐标为-1,点C的横坐标为1,
则线段AB先向右平移2个单位,
∵点B的横坐标为1,
∴点D的横坐标为3,即b=3,
点B的纵坐标为1,点D的纵坐标为4,
则线段AB向上平移3个单位,
∵点A的纵坐标为0,
∴点C的纵坐标为3,即a=3,
∴a+b=3+3=6,
故答案为:6.
19.(1,3)
【详解】解:∵顶点A(﹣3,4)的对应点是A1(2,5),
又
∴平移至的规律为:将向右平移5个单位,再向上平移1个单位即可得到
∵B(﹣4,2)
∴的坐标是(-4+5,2+1),即(1,3)
故答案为:(1,3)
20.(1008,0)
【详解】解:由图可知,4个点为一个循环组依次循环,
∵2016÷4=504,
∴点A2016是第504循环组的最后一个点,
504×2=1008,
∴点A2016的坐标为(1008,0).
故答案为(1008,0).
21.(1)高中楼,正东方向,正北方向,(2),;
【详解】(1)根据初中楼的坐标是,实验楼的坐标是,建立平面直角坐标系如图所示:
故答案为:高中楼,正东方向,正北方向;
(2)由(1)建立的直角坐标系得,
校门坐标(1,-3),图书馆坐标(4,1),
故答案为:,.
22.(1)图见详解
(2)
(3)图见详解,点的坐标为
【详解】(1)解:如图,△即为所求.
(2)解:由图可得:
.
的面积为.
(3)解:如图,即为所求.
由图可知点的坐标为.
23.(1)见解析
(2)
【详解】(1)解:如图:线段和即为所求.
(2)解:∵平移后得到
∴平移方式为“向下平移一个单位长度,向左平移3个单位长度”
∵
∴.
24.(1), ;(2),;(3)不可能,理由见解析.
【详解】解:点P到x轴的距离为1,,
点P到y轴的距离为2,,
如果点P可能在第一象限坐标轴夹角的平分线上点P在第一象限
,,不合题意
点P不可能在第一象限坐标轴夹角的平分线上.
25.(1)建立平面直角坐标系见解析,C(2,2),D(3,3),E(4,4),F(5,5);(2)11;10;(3)需要42平方米.
【详解】(1)建立平面直角坐标系如图所示,
C(2,2),D(3,3),E(4,4),F(5,5);
(2)台阶的长度:1×(10+1)=11,
高度:1×10=10;
(3)∵单位长度为1m,
∴地毯的长度为:(11+10)×1=21m,
∵台阶的宽度都是2m,
∴地毯的面积为21×2=42m2,
答:将这些台阶铺上地毯,需要42平方米.
