相似三角形的性质和判定[上学期]
图片预览








文档简介
课件20张PPT。相似三角形的性质和判定教学目标:
1.了解三角形相似及相似比的概念,掌握相似三角形的性质。
2.动手实践得到相似三角形的判定定理1,及运用判定定理1来判定两个三角形相似。引导
1.什么是相似图形?
把一个图形放大或缩小所得的图形与原图形是相似图形。
2.你的两个三角板是不是相似?和同学的有没有相似的?
3.教材P71图3-14△A`B`C`由
△ABC放大得到的,量一量它们的三个角和三条边,它们的三个角对应相等吗?
A`B`AB, B`C`BC,C`A`CA相等吗?我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形。
如果△ A`B`C`与△ABC相似且A`,B`,C`分别与A,B,C对应,那么记作
△ A`B`C` ∽ △ABCACBA’B’C’相似三角形的对应边的比K叫作相似比由相似三角形的定义可得相似三角形的
性质:相似三角形的三个角对应相等,三条边对应成比例。探究:
从上面知道,如果两个三角形相似,那么它们的三条边对应成比例。
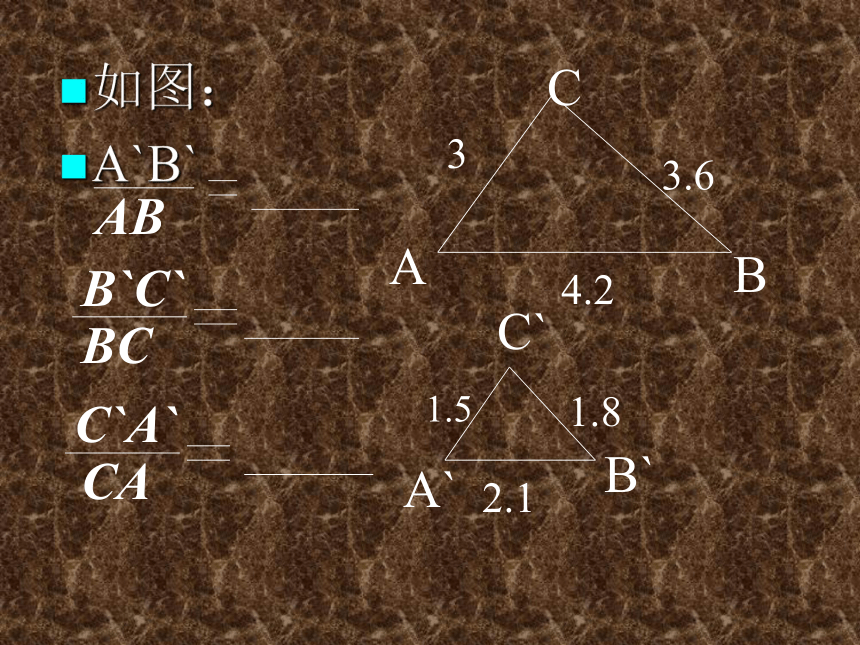
反之对吗?即,两个三角形的三条边对应成比例,那么两个三角形相似。如图:
A`B`ABCA`B`C`4.23.632.11.51.8ABB`C`BCC`A`CA量出? ABC和?A`B`C`的内角,
∠ A`与∠A相等吗? ∠B`与∠B相等吗? ∠C`与∠C相等吗?
△A`B`C`与△ABC相似吗?判定定理1:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
可以简单说成:三边对应成比例的两个三角形相似。论证:
运用相似三角形的概念解答;
1。两个全等三角形一定相似
吗?如果相似,那么相似比等于多少?由此你认为相似
与全等是什么关系?例1:已知△ A`B`C` ∽ △ABC
A`B`=3cm,AB=2.4cm,BC=1.6cm,∠B=650,∠C=750
求B`C`的长, ∠B`和∠A`的度数。
ABCB`C`32.41.6650750 A`解:∵△A`B`C`∽ △ABC
∴ BCA`B`AB由已知可得B`C`1.632.42(cm)由相似三角形的对应角相等可得: ∠ B`= ∠ B=650∠ C`=∠ C=750 ∴ ∠ A=1800 ― 650
750 400 ,B`C`例2.如图3-17中两个三角形是否相似?为什么?CABDEF3cm4cm3.5cm2.4cm2.1cm1.8cm 解:∵ DEAB2.440.6EFBC2.13.50.6FDCA1.830.6∴ DEABEFBCFDCA 从而△ DEF∽ △ABC (三边对应成比例的两个三角形相似)巩固
1。如图,D,E,F分别是△ABC
的边AB,BC,CA的中点,那么
△DEF∽ ,其相似比 ADBECF解:∵ DE,EF,DF均为△ ABC
的中位线
∴ DE AC12EFAB12DEBC12∴ DEACEFABDFBC12从而,△DEF∽ △CAB相似比为12,,应用:图1是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆绕点A转动,B端翘起。要使石头滚动, B端须向上翘起10cm,
杠杆达到A`B`
的位置。
如图2▲ ACB图1图2是受力分析图,此时,我们不难发现 △ ACD∽ △BCE,若AC与
BC之比是5∶1,要使这块石头滚动,
至少要将杠杆A端下压多少厘米?▲ AA`DCBEB`解:∵ △ ACD∽ △BCE
∴ AD∶ BE=AC ∶BC=5∶1
∴AD=5╳10=50(cm)
故至少要将A端下压50cm. ▲ AA`DCBEB`
1.了解三角形相似及相似比的概念,掌握相似三角形的性质。
2.动手实践得到相似三角形的判定定理1,及运用判定定理1来判定两个三角形相似。引导
1.什么是相似图形?
把一个图形放大或缩小所得的图形与原图形是相似图形。
2.你的两个三角板是不是相似?和同学的有没有相似的?
3.教材P71图3-14△A`B`C`由
△ABC放大得到的,量一量它们的三个角和三条边,它们的三个角对应相等吗?
A`B`AB, B`C`BC,C`A`CA相等吗?我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形。
如果△ A`B`C`与△ABC相似且A`,B`,C`分别与A,B,C对应,那么记作
△ A`B`C` ∽ △ABCACBA’B’C’相似三角形的对应边的比K叫作相似比由相似三角形的定义可得相似三角形的
性质:相似三角形的三个角对应相等,三条边对应成比例。探究:
从上面知道,如果两个三角形相似,那么它们的三条边对应成比例。
反之对吗?即,两个三角形的三条边对应成比例,那么两个三角形相似。如图:
A`B`ABCA`B`C`4.23.632.11.51.8ABB`C`BCC`A`CA量出? ABC和?A`B`C`的内角,
∠ A`与∠A相等吗? ∠B`与∠B相等吗? ∠C`与∠C相等吗?
△A`B`C`与△ABC相似吗?判定定理1:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。
可以简单说成:三边对应成比例的两个三角形相似。论证:
运用相似三角形的概念解答;
1。两个全等三角形一定相似
吗?如果相似,那么相似比等于多少?由此你认为相似
与全等是什么关系?例1:已知△ A`B`C` ∽ △ABC
A`B`=3cm,AB=2.4cm,BC=1.6cm,∠B=650,∠C=750
求B`C`的长, ∠B`和∠A`的度数。
ABCB`C`32.41.6650750 A`解:∵△A`B`C`∽ △ABC
∴ BCA`B`AB由已知可得B`C`1.632.42(cm)由相似三角形的对应角相等可得: ∠ B`= ∠ B=650∠ C`=∠ C=750 ∴ ∠ A=1800 ― 650
750 400 ,B`C`例2.如图3-17中两个三角形是否相似?为什么?CABDEF3cm4cm3.5cm2.4cm2.1cm1.8cm 解:∵ DEAB2.440.6EFBC2.13.50.6FDCA1.830.6∴ DEABEFBCFDCA 从而△ DEF∽ △ABC (三边对应成比例的两个三角形相似)巩固
1。如图,D,E,F分别是△ABC
的边AB,BC,CA的中点,那么
△DEF∽ ,其相似比 ADBECF解:∵ DE,EF,DF均为△ ABC
的中位线
∴ DE AC12EFAB12DEBC12∴ DEACEFABDFBC12从而,△DEF∽ △CAB相似比为12,,应用:图1是用杠杆撬石头的示意图,C是支点,当用力压杠杆的A端时,杠杆绕点A转动,B端翘起。要使石头滚动, B端须向上翘起10cm,
杠杆达到A`B`
的位置。
如图2▲ ACB图1图2是受力分析图,此时,我们不难发现 △ ACD∽ △BCE,若AC与
BC之比是5∶1,要使这块石头滚动,
至少要将杠杆A端下压多少厘米?▲ AA`DCBEB`解:∵ △ ACD∽ △BCE
∴ AD∶ BE=AC ∶BC=5∶1
∴AD=5╳10=50(cm)
故至少要将A端下压50cm. ▲ AA`DCBEB`
