2022—2023学年人教版数学七年级下册 5.1.3同位角、内错角、同旁内角课件(共33张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学七年级下册 5.1.3同位角、内错角、同旁内角课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 00:00:00 | ||
图片预览




文档简介
(共33张PPT)
5.1 相交线
5.1.3 同位角、内错角、同旁内角
人教版 数学 七年级 下册
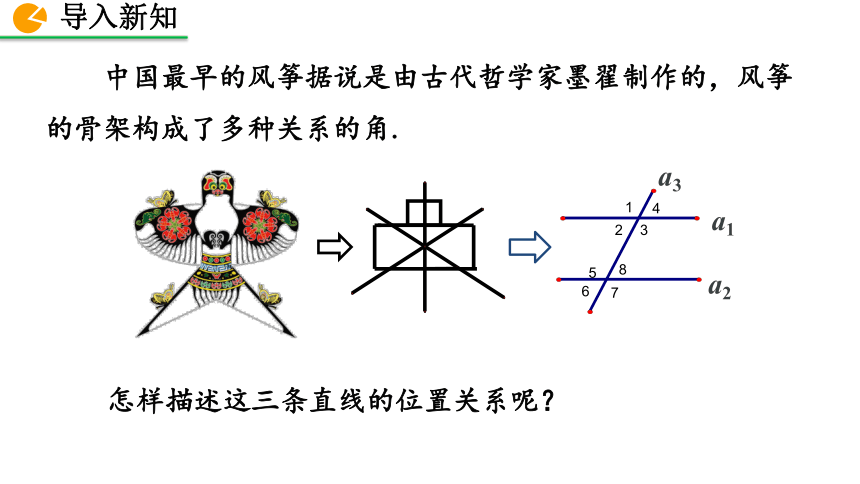
中国最早的风筝据说是由古代哲学家墨翟制作的,风筝的骨架构成了多种关系的角.
怎样描述这三条直线的位置关系呢?
导入新知
a1
a2
a3
1. 了解同位角、内错角、同旁内角的概念.
2. 会在简单的图形中辨认同位角、内错角、同旁内角.
学习目标
3. 会在给定某个条件下进行有关同位角、内错角、同旁内角的判定和计算.
三条直线相交可以分为哪些情况?
探究新知
对三条直线相交按交点的个数分为三种情况:
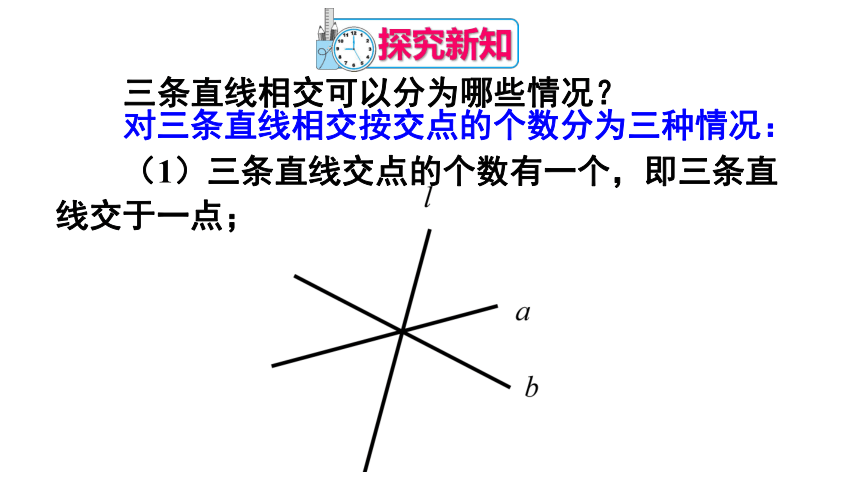
(1)三条直线交点的个数有一个,即三条直线交于一点;
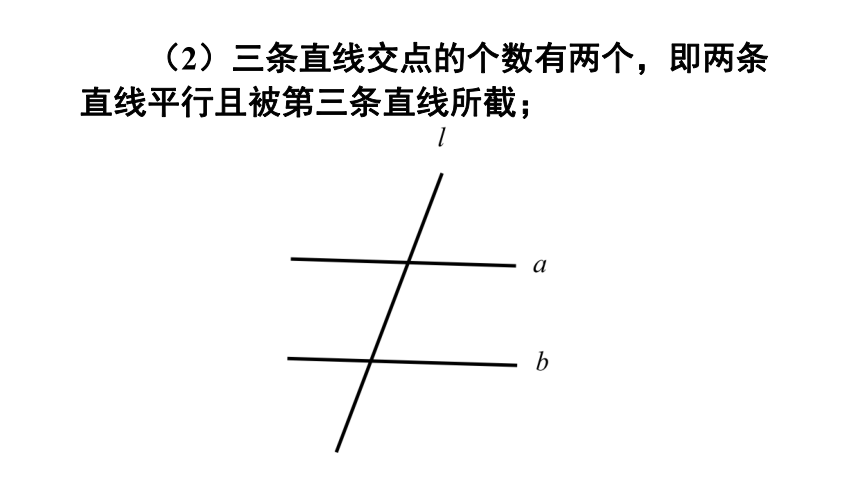
(2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;
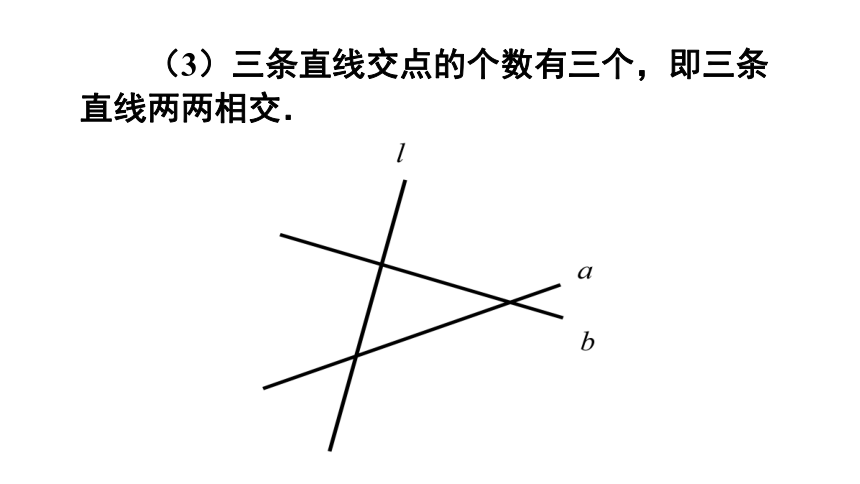
(3)三条直线交点的个数有三个,即三条直线两两相交.
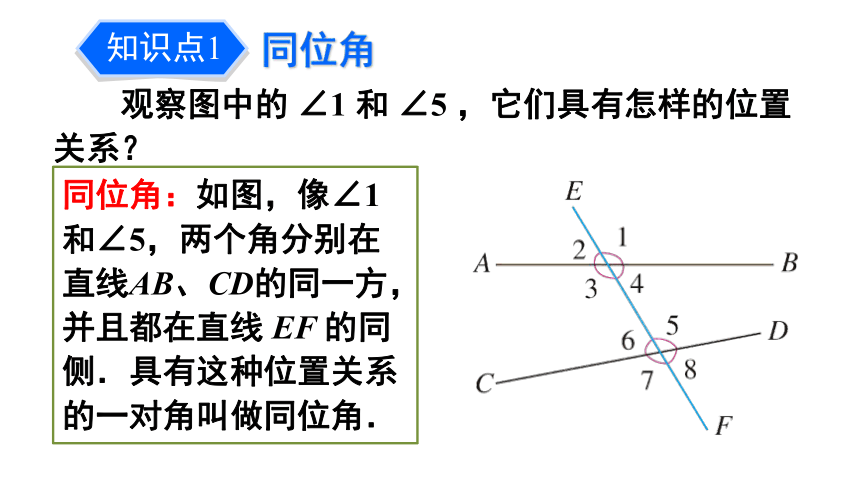
观察图中的 ∠1 和 ∠5 ,它们具有怎样的位置关系?
同位角:如图,像∠1和∠5,两个角分别在直线AB、CD的同一方,并且都在直线 EF 的同侧.具有这种位置关系的一对角叫做同位角.
知识点1
同位角
(1)你能找出图中还有哪几对角构成同位角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同位角?
(1)除了∠1 和∠5是同位角,还有∠2 和∠6,∠3 和∠7, ∠4 和∠8 也构成同位角.
(2)共有 4 对同位角.
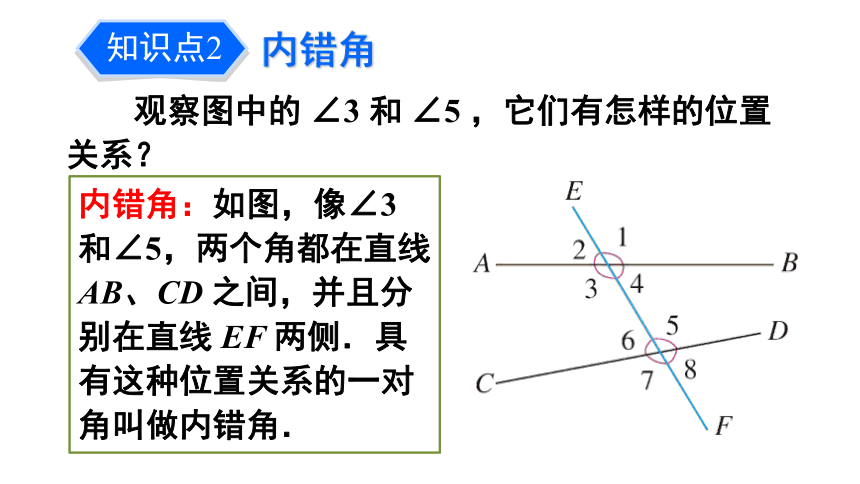
观察图中的 ∠3 和 ∠5 ,它们有怎样的位置关系?
内错角:如图,像∠3 和∠5,两个角都在直线 AB、CD 之间,并且分别在直线 EF 两侧.具有这种位置关系的一对角叫做内错角.
知识点2
内错角
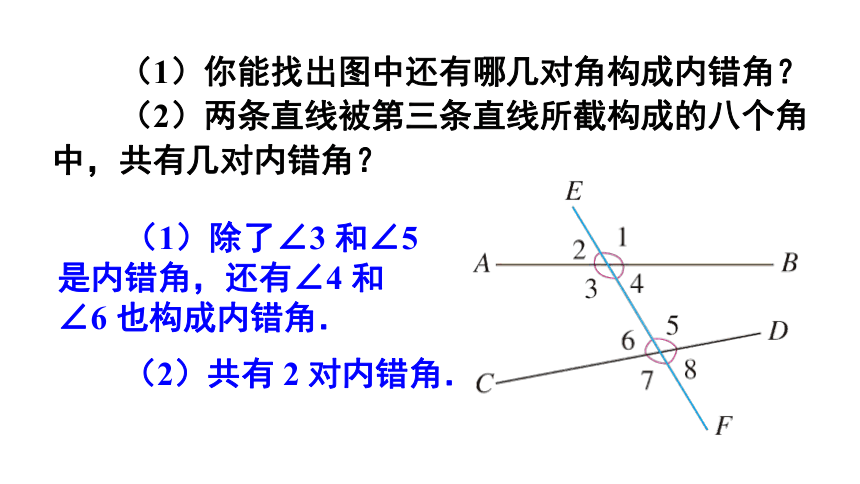
(1)你能找出图中还有哪几对角构成内错角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对内错角?
(1)除了∠3 和∠5是内错角,还有∠4 和∠6 也构成内错角.
(2)共有 2 对内错角.
如图,我们称∠3 和∠6 为同旁内角,你能根据两个角的特征,描述一下同旁内角的定义吗?
同旁内角:如图,像∠3和∠6,两个角都在直线AB、CD 之间,并且都在直线 EF 的同一旁.具有这种位置关系的一对角叫做同旁内角.
知识点3
同旁内角
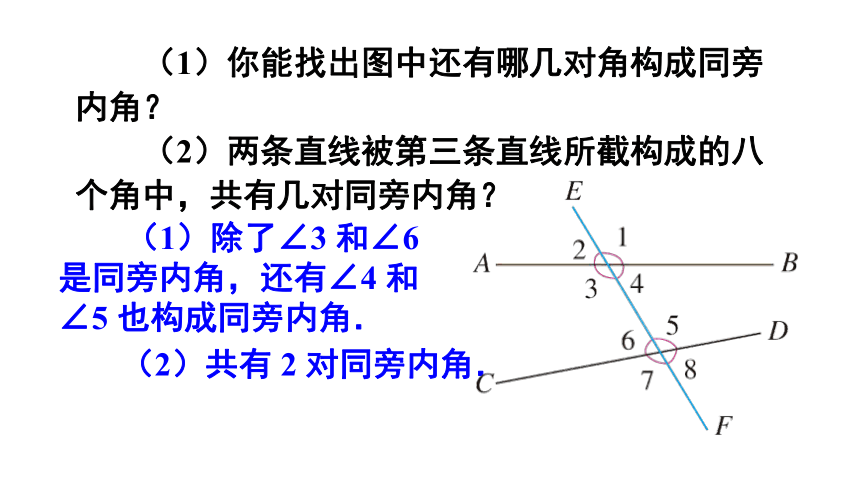
(1)你能找出图中还有哪几对角构成同旁内角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同旁内角?
(1)除了∠3 和∠6是同旁内角,还有∠4 和∠5 也构成同旁内角.
(2)共有 2 对同旁内角.
例 如图,直线 DE、BC 被直线 AB 所截,
(1)∠1 和∠2,∠1 和∠3,∠1 和∠4 各是什么位置关系的角?
∠1 与 ∠2 是内错角,
∠1 与∠3 是同旁内角,
∠1 与∠4 是同位角.
如果∠1=∠4,由对顶角相等,
得∠2=∠4,那么∠1=∠2.
因为∠4 和∠3 互补,得∠4 + ∠3=180 ,
又因为∠1 =∠4,
所以∠1 +∠3 = 180 ,
即∠1 和∠3 互补.
例 如图,直线 DE、BC 被直线 AB 所截,
(2)如果∠1=∠4,那么∠1 和∠2 相等吗?∠1 和∠3 互补吗?为什么?
1.分别指出下列图中的同位角、内错角、同旁内角.
练习
同位角:∠2 与∠6,∠4 与∠8,∠3 与∠7,∠1 与∠5
内错角:∠3 与∠6,∠4 与∠5
同旁内角:∠3 与∠5,∠4 与∠6
同位角:∠1 与∠3,∠2 与∠4.
内错角:无.
同旁内角:∠2 与 ∠3.
2. 如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
解:∠B 与∠DAB 是内错
角,与∠BAE 是同旁内角,它
们都是由 DE 与 BC 被 AB 所截
形成的,还与∠BAC 是同旁内
角,它们是由 AC、BC 被 BA 所截形成的. ∠C 与∠EAC 是内错角,与∠DAC 是同旁内角,它们都是由 DE 与 BC 被 AC 所截形成的. 还与∠BAC 是同旁内角,它们是由 AB、BC 被 AC 所截形成的.
1.如图,∠2 与∠3 是_______角,∠2 和∠4是_______角,∠2 与∠5 是_______角,∠2 与∠8是_______角,∠2 与∠6 是________角.
强化
邻补
内错
同位
同位
同旁内
2. 如图:
①∠DAE 的同位角是______,它们是直线______和直线______被直线______所截形成的.
②∠CAD 的内错角是______,它们是直线______和直线______被直线______所截形成的.
∠B
AD
BC
AB
∠C
AD
BC
AC
∠DAB,∠CAB,∠C
③∠B 的同旁内角有______________________.
1.如图,所标出的 7 个角中共有____对内错角,____对同位角,____对同旁内角.
误区一 对同位角、内错角、同旁内角的定义理解不透彻
错 解
正 解
5 4 4
4 2 4
错因分析
两条直线被第三条直线所截,这是判断同位角、内错角、同旁内角的前提条件,解答此题时,常常误认为∠4和∠6是同位角,∠3和∠5是同位角,∠4和∠7是内错角等,事实上这三对角中的每一对角都没有公共边.
2. 如图,∠1 与∠2,∠3 与∠4分别是内错角,它们分别是由哪两条直线被哪一条直线所截得到的?
误区二 由角反推三线时出错
错 解
∠1与∠2是直线AD与BC被直线AC所截得到 的,∠3与∠4是直线AB与DC被直线BD所截得到的.
正 解
∠1与∠2是直线AB与DC被直线AC所截得到 的,∠3与∠4是直线AD与BC被直线BD所截得到的.
错因分析
错解中没有分清∠1 与 ∠2,∠3 与∠4分别是由哪两条直线被第三条直线所截得到的,而导致错误. 应根据相关的概念来确定.
如图,∠B的同位角可以是( )
A.∠1 B.∠2
C.∠3 D.∠4
D
链接中考
1.如图,∠DAB和∠ABC的位置关系是( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
2.如图,∠1和∠2不能构成同位角的图形是( )
C
D
A
D
B
C
E
基础巩固题
课堂检测
A B C D
A
D
E
B
F
C
3.看图填空:
(1)如图1所示,若ED,BF被AB所截,则∠1与_____是同位角.
∠2
课堂检测
图1
A
D
E
B
F
C
A
D
E
B
F
C
(2)如图2,∠1与∠3是AB和AF被_____所截构成的 角;
DE
内错
(3)如图3,∠2与∠4是 和 被BC所截构成的____角.
AB
AF
同位
图2
图3
课堂检测
4.根据地图填空:
学校与游乐场所在的角形成一对( )角;
学校与超市所在的角形成一对( )角;
学校与飞机场所在的角形成一对( )角.
同位
同旁内
内错
课堂检测
∠A与∠8是哪两条直线被哪条直线所截的角 它们是什么关系的角 ∠A与∠5呢 ∠A与∠6呢
E
D
C
B
A
8
7
6
5
4
3
2
1
解:∠A与∠8是直线AB,DE被直线AC所截形成的内错角.
∠A与∠5是直线AB,DE被直线AC所截形成的同旁内角.
∠A与∠6是直线AB,DE被直线AC所截形成的同位角.
能力提升题
课堂检测
如图所示,指出图中各对角的位置关系:
(1)∠C和∠D是 角;
(2)∠B和∠GEF是 角;
(3)∠A和∠D是 角,
∠B和∠C也是 角;
(4)∠AGE和∠BGE是 角;
(5)∠CFD和∠AFB是 角.
同旁内
同位
内错
内错
邻补
对顶
拓广探索题
课堂检测
同位角
内错角
同旁内角
生活中的数学:三线八角手势记忆法
课堂小结
1.这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角.
2.同位角、内错角、同旁内角的特点:
与被截直线的关系 与截线的关系
同位角
内错角
同旁内角
被截直线的同旁
被截直线之间
被截直线之间
截线的同旁
截线的两旁
截线的同旁
课堂小结
5.1 相交线
5.1.3 同位角、内错角、同旁内角
人教版 数学 七年级 下册
中国最早的风筝据说是由古代哲学家墨翟制作的,风筝的骨架构成了多种关系的角.
怎样描述这三条直线的位置关系呢?
导入新知
a1
a2
a3
1. 了解同位角、内错角、同旁内角的概念.
2. 会在简单的图形中辨认同位角、内错角、同旁内角.
学习目标
3. 会在给定某个条件下进行有关同位角、内错角、同旁内角的判定和计算.
三条直线相交可以分为哪些情况?
探究新知
对三条直线相交按交点的个数分为三种情况:
(1)三条直线交点的个数有一个,即三条直线交于一点;
(2)三条直线交点的个数有两个,即两条直线平行且被第三条直线所截;
(3)三条直线交点的个数有三个,即三条直线两两相交.
观察图中的 ∠1 和 ∠5 ,它们具有怎样的位置关系?
同位角:如图,像∠1和∠5,两个角分别在直线AB、CD的同一方,并且都在直线 EF 的同侧.具有这种位置关系的一对角叫做同位角.
知识点1
同位角
(1)你能找出图中还有哪几对角构成同位角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同位角?
(1)除了∠1 和∠5是同位角,还有∠2 和∠6,∠3 和∠7, ∠4 和∠8 也构成同位角.
(2)共有 4 对同位角.
观察图中的 ∠3 和 ∠5 ,它们有怎样的位置关系?
内错角:如图,像∠3 和∠5,两个角都在直线 AB、CD 之间,并且分别在直线 EF 两侧.具有这种位置关系的一对角叫做内错角.
知识点2
内错角
(1)你能找出图中还有哪几对角构成内错角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对内错角?
(1)除了∠3 和∠5是内错角,还有∠4 和∠6 也构成内错角.
(2)共有 2 对内错角.
如图,我们称∠3 和∠6 为同旁内角,你能根据两个角的特征,描述一下同旁内角的定义吗?
同旁内角:如图,像∠3和∠6,两个角都在直线AB、CD 之间,并且都在直线 EF 的同一旁.具有这种位置关系的一对角叫做同旁内角.
知识点3
同旁内角
(1)你能找出图中还有哪几对角构成同旁内角?
(2)两条直线被第三条直线所截构成的八个角中,共有几对同旁内角?
(1)除了∠3 和∠6是同旁内角,还有∠4 和∠5 也构成同旁内角.
(2)共有 2 对同旁内角.
例 如图,直线 DE、BC 被直线 AB 所截,
(1)∠1 和∠2,∠1 和∠3,∠1 和∠4 各是什么位置关系的角?
∠1 与 ∠2 是内错角,
∠1 与∠3 是同旁内角,
∠1 与∠4 是同位角.
如果∠1=∠4,由对顶角相等,
得∠2=∠4,那么∠1=∠2.
因为∠4 和∠3 互补,得∠4 + ∠3=180 ,
又因为∠1 =∠4,
所以∠1 +∠3 = 180 ,
即∠1 和∠3 互补.
例 如图,直线 DE、BC 被直线 AB 所截,
(2)如果∠1=∠4,那么∠1 和∠2 相等吗?∠1 和∠3 互补吗?为什么?
1.分别指出下列图中的同位角、内错角、同旁内角.
练习
同位角:∠2 与∠6,∠4 与∠8,∠3 与∠7,∠1 与∠5
内错角:∠3 与∠6,∠4 与∠5
同旁内角:∠3 与∠5,∠4 与∠6
同位角:∠1 与∠3,∠2 与∠4.
内错角:无.
同旁内角:∠2 与 ∠3.
2. 如图,∠B 与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C 进行同样的讨论.
解:∠B 与∠DAB 是内错
角,与∠BAE 是同旁内角,它
们都是由 DE 与 BC 被 AB 所截
形成的,还与∠BAC 是同旁内
角,它们是由 AC、BC 被 BA 所截形成的. ∠C 与∠EAC 是内错角,与∠DAC 是同旁内角,它们都是由 DE 与 BC 被 AC 所截形成的. 还与∠BAC 是同旁内角,它们是由 AB、BC 被 AC 所截形成的.
1.如图,∠2 与∠3 是_______角,∠2 和∠4是_______角,∠2 与∠5 是_______角,∠2 与∠8是_______角,∠2 与∠6 是________角.
强化
邻补
内错
同位
同位
同旁内
2. 如图:
①∠DAE 的同位角是______,它们是直线______和直线______被直线______所截形成的.
②∠CAD 的内错角是______,它们是直线______和直线______被直线______所截形成的.
∠B
AD
BC
AB
∠C
AD
BC
AC
∠DAB,∠CAB,∠C
③∠B 的同旁内角有______________________.
1.如图,所标出的 7 个角中共有____对内错角,____对同位角,____对同旁内角.
误区一 对同位角、内错角、同旁内角的定义理解不透彻
错 解
正 解
5 4 4
4 2 4
错因分析
两条直线被第三条直线所截,这是判断同位角、内错角、同旁内角的前提条件,解答此题时,常常误认为∠4和∠6是同位角,∠3和∠5是同位角,∠4和∠7是内错角等,事实上这三对角中的每一对角都没有公共边.
2. 如图,∠1 与∠2,∠3 与∠4分别是内错角,它们分别是由哪两条直线被哪一条直线所截得到的?
误区二 由角反推三线时出错
错 解
∠1与∠2是直线AD与BC被直线AC所截得到 的,∠3与∠4是直线AB与DC被直线BD所截得到的.
正 解
∠1与∠2是直线AB与DC被直线AC所截得到 的,∠3与∠4是直线AD与BC被直线BD所截得到的.
错因分析
错解中没有分清∠1 与 ∠2,∠3 与∠4分别是由哪两条直线被第三条直线所截得到的,而导致错误. 应根据相关的概念来确定.
如图,∠B的同位角可以是( )
A.∠1 B.∠2
C.∠3 D.∠4
D
链接中考
1.如图,∠DAB和∠ABC的位置关系是( )
A.同位角 B.同旁内角
C.内错角 D.以上结论都不对
2.如图,∠1和∠2不能构成同位角的图形是( )
C
D
A
D
B
C
E
基础巩固题
课堂检测
A B C D
A
D
E
B
F
C
3.看图填空:
(1)如图1所示,若ED,BF被AB所截,则∠1与_____是同位角.
∠2
课堂检测
图1
A
D
E
B
F
C
A
D
E
B
F
C
(2)如图2,∠1与∠3是AB和AF被_____所截构成的 角;
DE
内错
(3)如图3,∠2与∠4是 和 被BC所截构成的____角.
AB
AF
同位
图2
图3
课堂检测
4.根据地图填空:
学校与游乐场所在的角形成一对( )角;
学校与超市所在的角形成一对( )角;
学校与飞机场所在的角形成一对( )角.
同位
同旁内
内错
课堂检测
∠A与∠8是哪两条直线被哪条直线所截的角 它们是什么关系的角 ∠A与∠5呢 ∠A与∠6呢
E
D
C
B
A
8
7
6
5
4
3
2
1
解:∠A与∠8是直线AB,DE被直线AC所截形成的内错角.
∠A与∠5是直线AB,DE被直线AC所截形成的同旁内角.
∠A与∠6是直线AB,DE被直线AC所截形成的同位角.
能力提升题
课堂检测
如图所示,指出图中各对角的位置关系:
(1)∠C和∠D是 角;
(2)∠B和∠GEF是 角;
(3)∠A和∠D是 角,
∠B和∠C也是 角;
(4)∠AGE和∠BGE是 角;
(5)∠CFD和∠AFB是 角.
同旁内
同位
内错
内错
邻补
对顶
拓广探索题
课堂检测
同位角
内错角
同旁内角
生活中的数学:三线八角手势记忆法
课堂小结
1.这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,即同位角、内错角、同旁内角.
2.同位角、内错角、同旁内角的特点:
与被截直线的关系 与截线的关系
同位角
内错角
同旁内角
被截直线的同旁
被截直线之间
被截直线之间
截线的同旁
截线的两旁
截线的同旁
课堂小结
