18.12.平行四边形的判定(2) 课件(22张ppt)
文档属性
| 名称 | 18.12.平行四边形的判定(2) 课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 09:35:17 | ||
图片预览





文档简介
(共22张PPT)
18.1.2平行四边形的判定(2)
人教版版八年级下册
教学目标
1.掌握“一组对边平行且相等的四边形是平行四边形”
的判定方法.(重点)
2.会进行平行四边形的性质与判定的综合运用.(难点)
情景导入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
新知讲解
问题 我们知道,两组对边分别平行或相等的是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
猜想1:一组对边相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形
等腰梯形不是平行四边形,因而此猜想错误.
猜想2:一组对边平行的四边形是平行四边形.
梯形的上下底平行,但不是平行四边形,因而此猜想错误.
新知讲解
B
A
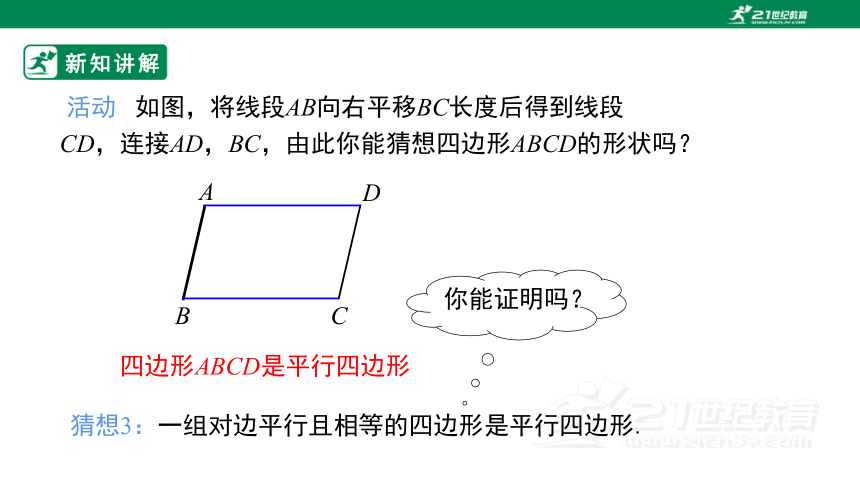
活动 如图,将线段AB向右平移BC长度后得到线段 CD,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
D
C
四边形ABCD是平行四边形
猜想3:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
新知讲解
A
B
C
D
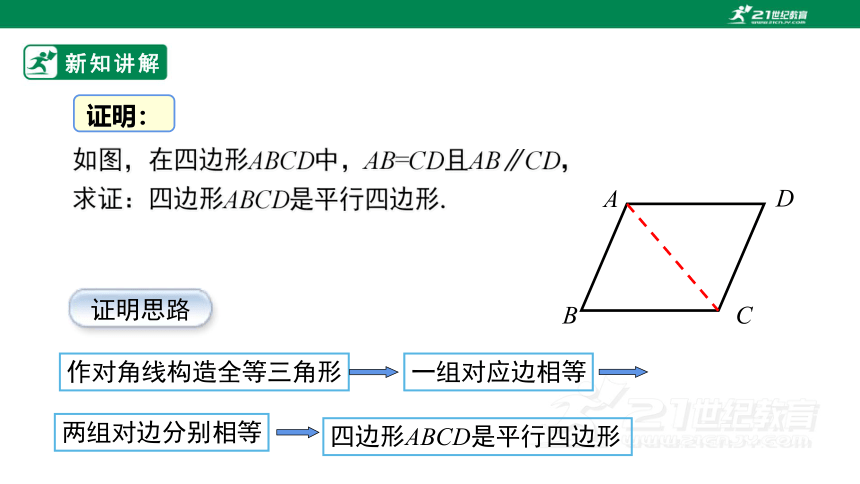
证明思路
作对角线构造全等三角形
一组对应边相等
两组对边分别相等
四边形ABCD是平行四边形
如图,在四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证明:
新知讲解
A
B
C
D
2
1
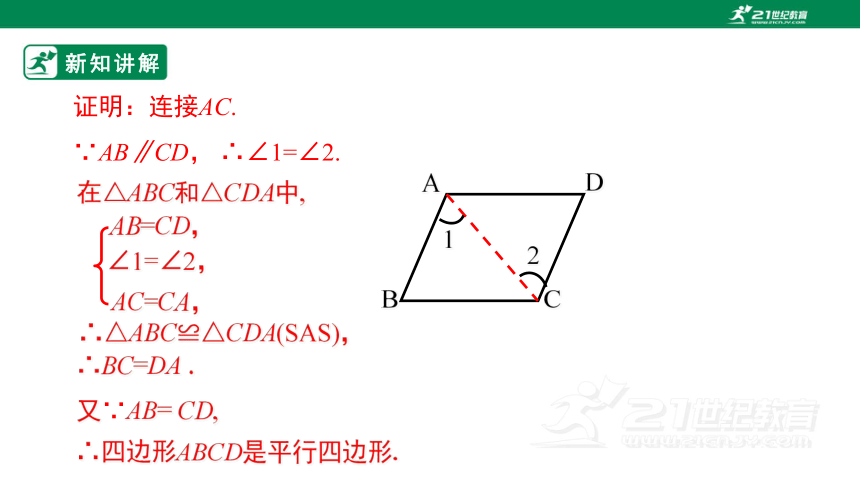
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .
又∵AB= CD,
∴四边形ABCD是平行四边形.
新知讲解
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
归纳:
例题讲解
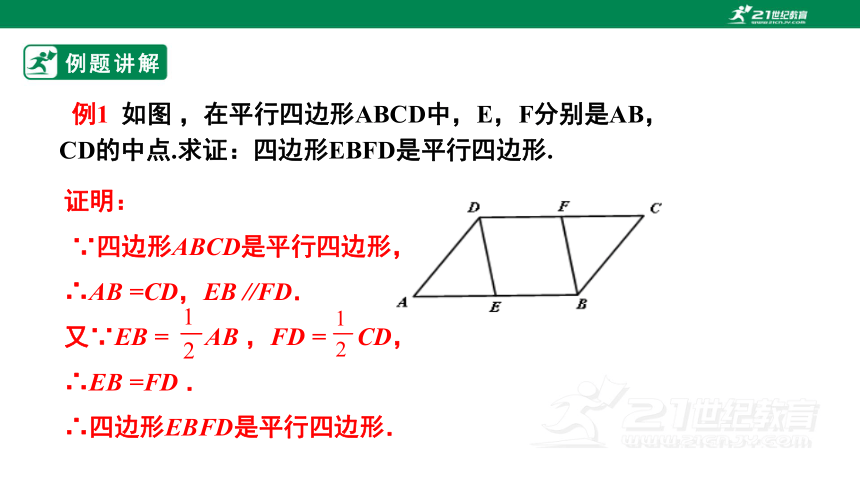
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例1 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
针对练习
1.在 ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是 ( )
A.AF=CE B.AE=CF
C.∠BAE=∠FCD D.∠BEA=∠FCE
B
针对练习
2. 已知四边形ABCD中,AB∥CD,AB=CD,周长为40cm,两邻边的比是3:2,则较大边的长度是( )
A.8cm B.10cm
C.12cm D.14cm
C
3.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有____个.
9
例题讲解
例2 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=BD ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
针对练习
4、如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE.
(2)求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS),
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE,
∴CD∥BE.
又∵CD=BE,
∴四边形CBED是平行四边形.
例题讲解
例3 如图,△ABC中,BD平分∠ABC,DF∥BC,EF∥AC,试问BF与CE相等吗?为什么?
解:BF=CE.理由如下:
∵DF∥BC,EF∥AC,
∴四边形FECD是平行四边形,∠FDB=∠DBE,
∴FD=CE.
∵BD平分∠ABC,
∴∠FBD=∠EBD,
∴∠FBD=∠FDB.
∴BF=FD.
∴BF=CE.
例题讲解
例4 如图,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.求证:四边形BCED′是平行四边形.
证明:由题意得∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′.
例题讲解
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴CE∥D′B,CE=D′B,
∴四边形BCED′是平行四边形.
此题利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,再结合平行四边形的判定及性质进行解题.
归纳
课堂总结
平行四边形的判定(2)
平行四边形的性质与判定的综合运用
一组对边平行且相等的四边形是平行四边形.
拓展提升
1.如图, ABCD中,E,G,F,H分别是四条边上的点,且AE=CF,BG=DH.求证:EF与GH互相平分.
证明:连接EG,GF,FH,HE,∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB.
∵BG=DH,∴AH=CG,
又AE=CF,
∴△AEH≌△CFG,
∴HE=GF,
同理可得:EG=FH,
∴四边形EGFH是平行四边形,∴EF与GH互相平分.
拓展提升
2.如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________;CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
拓展提升
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
18.1.2平行四边形的判定(2)
人教版版八年级下册
教学目标
1.掌握“一组对边平行且相等的四边形是平行四边形”
的判定方法.(重点)
2.会进行平行四边形的性质与判定的综合运用.(难点)
情景导入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
新知讲解
问题 我们知道,两组对边分别平行或相等的是平行四边形.如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
猜想1:一组对边相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形
等腰梯形不是平行四边形,因而此猜想错误.
猜想2:一组对边平行的四边形是平行四边形.
梯形的上下底平行,但不是平行四边形,因而此猜想错误.
新知讲解
B
A
活动 如图,将线段AB向右平移BC长度后得到线段 CD,连接AD,BC,由此你能猜想四边形ABCD的形状吗?
D
C
四边形ABCD是平行四边形
猜想3:一组对边平行且相等的四边形是平行四边形.
你能证明吗?
新知讲解
A
B
C
D
证明思路
作对角线构造全等三角形
一组对应边相等
两组对边分别相等
四边形ABCD是平行四边形
如图,在四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证明:
新知讲解
A
B
C
D
2
1
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
AB=CD,
AC=CA,
∠1=∠2,
∴△ABC≌△CDA(SAS),
∴BC=DA .
又∵AB= CD,
∴四边形ABCD是平行四边形.
新知讲解
平行四边形的判定定理:
一组对边平行且相等的四边形是平行四边形.
几何语言描述:
在四边形ABCD中,∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
B
D
A
C
归纳:
例题讲解
证明:
∵四边形ABCD是平行四边形,
∴AB =CD,EB //FD.
又∵EB = AB ,FD = CD,
∴EB =FD .
∴四边形EBFD是平行四边形.
例1 如图 ,在平行四边形ABCD中,E,F分别是AB,CD的中点.求证:四边形EBFD是平行四边形.
针对练习
1.在 ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是 ( )
A.AF=CE B.AE=CF
C.∠BAE=∠FCD D.∠BEA=∠FCE
B
针对练习
2. 已知四边形ABCD中,AB∥CD,AB=CD,周长为40cm,两邻边的比是3:2,则较大边的长度是( )
A.8cm B.10cm
C.12cm D.14cm
C
3.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,则图中的平行四边形共有____个.
9
例题讲解
例2 如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=BD ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
针对练习
4、如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE.
(2)求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS),
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE,
∴CD∥BE.
又∵CD=BE,
∴四边形CBED是平行四边形.
例题讲解
例3 如图,△ABC中,BD平分∠ABC,DF∥BC,EF∥AC,试问BF与CE相等吗?为什么?
解:BF=CE.理由如下:
∵DF∥BC,EF∥AC,
∴四边形FECD是平行四边形,∠FDB=∠DBE,
∴FD=CE.
∵BD平分∠ABC,
∴∠FBD=∠EBD,
∴∠FBD=∠FDB.
∴BF=FD.
∴BF=CE.
例题讲解
例4 如图,将 ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕l交CD边于点E,连接BE.求证:四边形BCED′是平行四边形.
证明:由题意得∠DAE=∠D′AE,∠DEA=∠D′EA,∠D=∠AD′E,
∵DE∥AD′,
∴∠DEA=∠EAD′,
∴∠DAE=∠EAD′=∠DEA=∠D′EA,
∴∠DAD′=∠DED′,
∴四边形DAD′E是平行四边形,
∴DE=AD′.
例题讲解
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴CE∥D′B,CE=D′B,
∴四边形BCED′是平行四边形.
此题利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,再结合平行四边形的判定及性质进行解题.
归纳
课堂总结
平行四边形的判定(2)
平行四边形的性质与判定的综合运用
一组对边平行且相等的四边形是平行四边形.
拓展提升
1.如图, ABCD中,E,G,F,H分别是四条边上的点,且AE=CF,BG=DH.求证:EF与GH互相平分.
证明:连接EG,GF,FH,HE,∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB.
∵BG=DH,∴AH=CG,
又AE=CF,
∴△AEH≌△CFG,
∴HE=GF,
同理可得:EG=FH,
∴四边形EGFH是平行四边形,∴EF与GH互相平分.
拓展提升
2.如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含t的代数式表示:
AP=_____; DP=________;
BQ=________;CQ=________;
tcm
(12-t)cm
(15-2t)cm
2tcm
拓展提升
(2)当t为何值时,四边形APQB是平行四边形?
解:根据题意有AP=tcm,CQ=2tcm,
PD=(12-t)cm,BQ=(15-2t)cm.
∵AD∥BC,
∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15-2t,
解得t=5.
∴t=5s时四边形APQB是平行四边形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
