第十章:数据的收集、整理与描述练习题(含解析)2021-2022学年北京市各地七年级下学期数学期末试题选编
文档属性
| 名称 | 第十章:数据的收集、整理与描述练习题(含解析)2021-2022学年北京市各地七年级下学期数学期末试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-28 14:03:40 | ||
图片预览



文档简介
第十章:数据的收集、整理与描述练习题
一、单选题
1.(2022春·北京延庆·七年级统考期末)某同学要调查、分析本校七年级(1)班学生的身高状况,作为三年中跟踪调查的依据.
以下是排乱的统计步骤:
①绘制扇形统计图来表示各个身高范围所占的百分比;
②去校医务室收集学生入学后体检的有关数据;
③从扇形统计图中分析出学生身高状况;
④整理收集的相关数据,并按身高范围进行分组,在表格中表示出来.
正确统计步骤的顺序是( )
A.②→③→①→④ B.③→④→①→②
C.①→②→④→③ D.②→④→①→③
2.(2022春·北京东城·七年级统考期末)在以下四个有关统计调查的说法中,正确的是( )
A.全面调查适用于所有的调查
B.为了解全体学生的视力,对每位学生进行视力检查,是全面调查
C.为调查小区1500户家庭用水情况,抽取该小区100户家庭,样本容量为1500
D.为了解全校中学生的身高,以该校篮球队队员的身高作为样本,能客观估计总体
3.(2022春·北京昌平·七年级统考期末)下列调查中,适合用全面调查的是( )
A.了解20万只节能灯的使用寿命 B.了解某班35名学生的视力情况
C.了解某条河流的水质情况 D.了解全国居民对“垃圾分类”有关内容的认识程度
4.(2022春·北京延庆·七年级统考期末)下列调查方式,适合全面调查的是( )
A.调查北京市中学生每周体育锻炼时间 B.调查神舟十四号飞船零部件的质量
C.调查某一批次的计算器的使用寿命 D.调查全国中学生的视力情况
5.(2022春·北京丰台·七年级统考期末)下列调查方式,你认为最合适的是( )
A.对某地区饮用水矿物质含量的调查,采用抽样调查方式
B.旅客上飞机前的安全检查,采用抽样调查方式
C.对某班学生的校服尺寸大小的调查,采用抽样调查方式
D.调查某批次汽车的抗撞击能力,采用全面调查方式
6.(2022春·北京怀柔·七年级校考期末)下列调查活动,适合使用全面调查的是( )
A.调查某班同学课外体育锻炼时间; B.调查全市植树节中栽植树苗的成活率;
C.调查某种品牌照明灯的使用寿命; D.调查抗美援朝纪录片《为了和平》在线收视率.
7.(2022春·北京通州·七年级统考期末)下列调查方式,你认为最合适的是( )
A.对端午节期间市场上粽子质量情况,采用全面调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C.调查本市居民对“垃圾分类”有关内容的了解程度,采用全面调查方式
D.调查“神舟十一号”飞船重要零部件的产品质量,采用全面调查方式
8.(2022春·北京朝阳·七年级统考期末)下面的统计图反映了2013-2020年北京市人均可支配收入和人均消费支出的情况.
根据统计图提供的信息,下面有三个推断:
①2013-2020年,北京市人均可支配收入逐年增加;
②2013-2020年,北京市人均消费支出逐年增加;
③2019年北京市的人均可支配收入比人均消费支出约多2.47万元.
其中所有合理推断的序号是( )
A.① B.②③ C.①③ D.①②③
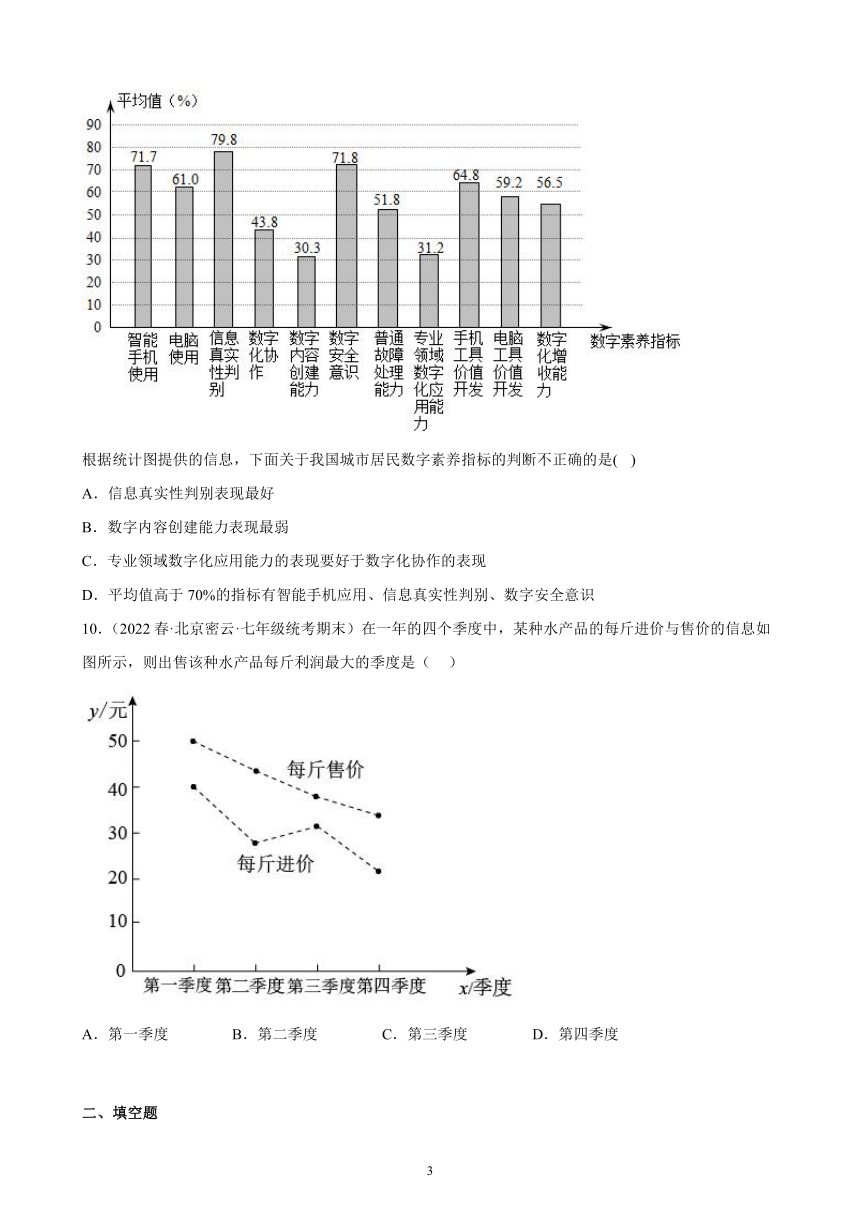
9.(2022春·北京西城·七年级统考期末)在《2016-2021年中国公民数字素养研究报告》中,中国社会科学院信息化研究中心课题组对我国城市居民的数字素养展开评估.下面是根据我国城市居民的11项数字素养平均值制作的统计图.
根据统计图提供的信息,下面关于我国城市居民数字素养指标的判断不正确的是( )
A.信息真实性判别表现最好
B.数字内容创建能力表现最弱
C.专业领域数字化应用能力的表现要好于数字化协作的表现
D.平均值高于70%的指标有智能手机应用、信息真实性判别、数字安全意识
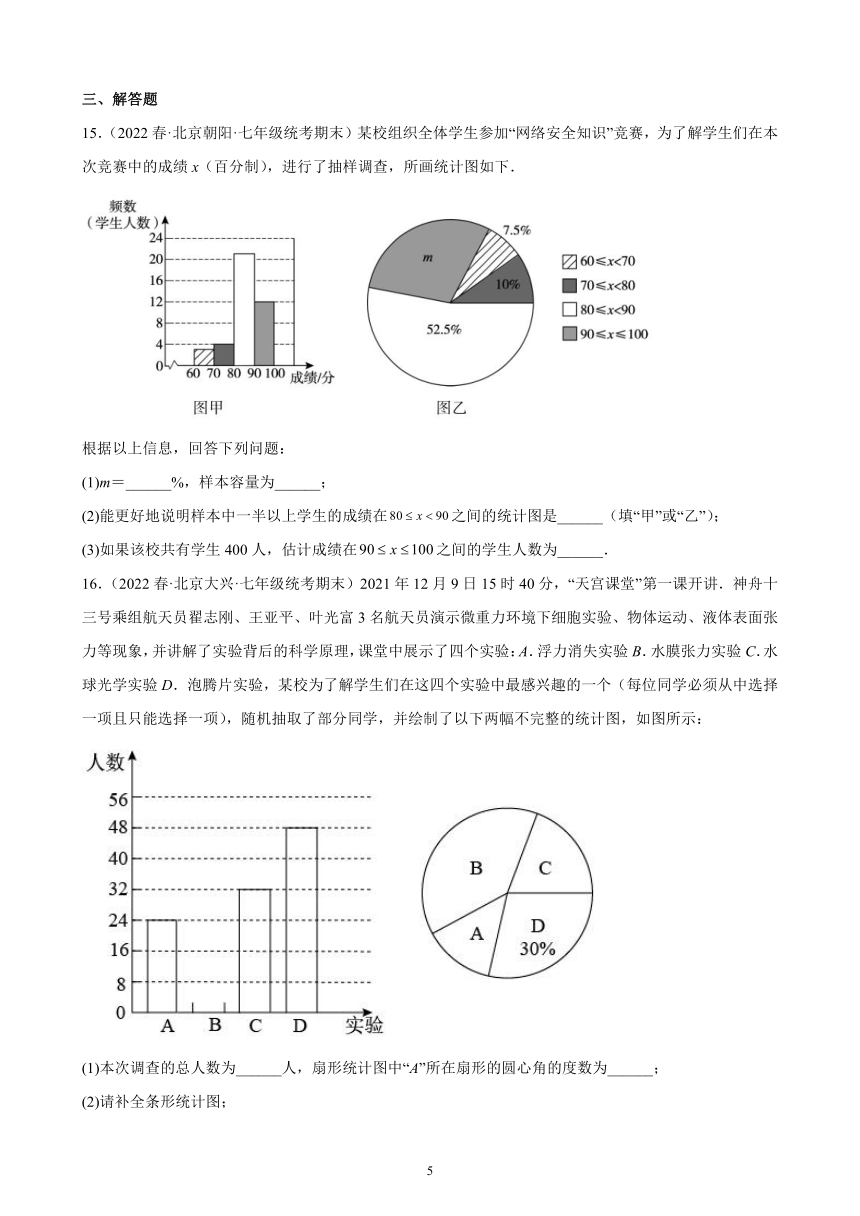
10.(2022春·北京密云·七年级统考期末)在一年的四个季度中,某种水产品的每斤进价与售价的信息如图所示,则出售该种水产品每斤利润最大的季度是( )
A.第一季度 B.第二季度 C.第三季度 D.第四季度
二、填空题
11.(2022春·北京海淀·七年级统考期末)如图是一家灯泡生产厂商的广告图,请从统计学角度判断广告语是否合适,并说明理由:_____________________
12.(2022春·北京丰台·七年级统考期末)某学校为调查学生对《中华人民共和国未成年人保护法》了解的情况,随机抽取部分学生进行调查,并将调查结果绘制成扇形统计图.如图,对该法“非常清楚”的学生对应扇形的圆心角度数为______.
13.(2022春·北京朝阳·七年级统考期末)下列调查:①调查全市中学生对2022年“中国航天日”主题“航天点亮梦想”的了解情况;②检测某批次节能灯的使用寿命;③选出某体育运动学校速度滑冰成绩最好的学生参加全国比赛,其中适合采用抽样调查的是______(写出所有正确答案的序号).
14.(2022春·北京顺义·七年级统考期末)某校利用课后服务时间,开设了A,B,C,D,E五类课程.某小组利用课余时间从全校1200名学生中抽取50名学生进行了“你最喜爱的课程”的抽样调查(每个被调查的学生必须选择而且只能选择其中一项),并将调查结果绘制成如下统计图:
则图2中B类课程对应扇形的圆心角为_______°,估计该校1200名学生喜欢D类课程的人数约为_______.
三、解答题
15.(2022春·北京朝阳·七年级统考期末)某校组织全体学生参加“网络安全知识”竞赛,为了解学生们在本次竞赛中的成绩x(百分制),进行了抽样调查,所画统计图如下.
根据以上信息,回答下列问题:
(1)m=______%,样本容量为______;
(2)能更好地说明样本中一半以上学生的成绩在之间的统计图是______(填“甲”或“乙”);
(3)如果该校共有学生400人,估计成绩在之间的学生人数为______.
16.(2022春·北京大兴·七年级统考期末)2021年12月9日15时40分,“天宫课堂”第一课开讲.神舟十三号乘组航天员翟志刚、王亚平、叶光富3名航天员演示微重力环境下细胞实验、物体运动、液体表面张力等现象,并讲解了实验背后的科学原理,课堂中展示了四个实验:A.浮力消失实验B.水膜张力实验C.水球光学实验D.泡腾片实验,某校为了解学生们在这四个实验中最感兴趣的一个(每位同学必须从中选择一项且只能选择一项),随机抽取了部分同学,并绘制了以下两幅不完整的统计图,如图所示:
(1)本次调查的总人数为______人,扇形统计图中“A”所在扇形的圆心角的度数为______;
(2)请补全条形统计图;
(3)若该校共有1200名同学,请根据抽样调查数据估计该校同学中对“水球光学实验”最感兴趣的人数.
17.(2022春·北京石景山·七年级统考期末)某学校体育兴趣小组,为了更好的开展活动,需要了解学校1000名学生对A,B,C,D四项体育活动的喜好情况,随机抽取了100名学生进行了“你最喜欢哪种运动”的调查(必选且只选一种),根据调查绘制了条形统计图和扇形统计图,部分信息如下:
(1)在抽取的100人中最喜欢运动项目A的人数为 ;
(2)求扇形统计图中“C”对应扇形的圆心角度数;
(3)补全条形统计图;
(4)依据本次调查结果,估计全校1000人名学生中最喜欢B运动项目的人数.
18.(2022春·北京延庆·七年级统考期末)某区图书馆充分发挥数字教育资源优势,利用“数字图书馆”组织开展了主题为“居家数字阅读+悦读”的中小学生寒假阅读主题活动.某校随机抽取了七年级的若干学生进行调查,并将所收集的数据分组整理,绘制了如下两幅不完整的统计图表,请根据图表信息回答下列问题.
七年级学生每天阅读时长情况统计表
组别 阅读时长(单位:小时) 人数(单位:人)
A 0<x≤0.5
B 0.5<x≤1 72
C 1<x≤1.5 18
D 1.5<x≤2
根据以上信息,回答下列问题:
(1)求出表中a,b的值;
(2)已知该校七年级的学生有1000人,试估计该校七年级学生每天阅读时长在0.5<x≤1.5的共有多少人?
19.(2022春·北京海淀·七年级统考期末)清朝康熙年间编校的《全唐诗》包含四万多首诗歌,逾三百万字,是后人研究唐诗的重要资源.小云利用统计知识分析《全唐诗》中李白和杜甫作品的风格差异.下面给出了部分信息:
a.《全唐诗》中,李白和杜甫分别有896和1158首作品.
b.二人作品中与“风”相关的词语频数统计表如下:
词语 频 数 诗人 春风 东风 清风 悲风 秋风 北风
李白 72 24 28 6 26 8
杜甫 19 4 6 10 30 14
c.通过统计二人的个性化用字,可绘制一种视觉效果更强的“词云图”,出现次数较多的关键字被予以视觉上的突出.
注:在文学作品中,东风即春风,常含有生机勃勃之意和喜春之情,如:等闲识得东风面,万紫千红总是春;北风通常寄寓诗人凄苦的情怀,抒写伤别之情,如:千里黄云白日曛,北风吹雁雪纷纷.
根据以上信息,回答下列问题:
(1)补全条形统计图:
(2)在与“风”相关的词语中,李白最常使用的词语是________,大约每________首诗歌中就会出现一次该词语(结果取整数),而杜甫最常使用的词语是________;
(3)下列推断合理的是________.
①相较于杜甫,与“风”有关的词语在李白的诗歌中更常见;
②个性化用字中,李白最常使用的汉字是“水”,杜甫则是“江”;
③李白更常用“风”表达喜悦,而杜甫更常用“风”表达悲伤.
20.(2022春·北京西城·七年级统考期末)故宫博物院为鼓励游客参与“故宫零废弃”项目做好垃圾分类,在“数字故宫”小程序中推出了一项体验活动,将故宫改造升级后的垃圾桶编号并精心布局,在每个垃圾桶点位(共79个)设置一道与院内场景相关的篆体古字题目,游客点击相应点位的垃圾桶编号解答题目,以形会意,看字识“物”,并在感受中国传统文化的同时,了解垃圾分类知识.
王老师在全年级随机邀请了40名学生在线参与答题,小明所在小组收集、整理同学们看字识“物”和辨别垃圾的答题成绩并制作统计图表(成绩设为百分制).下面是这40名学生成绩的频数分布表、频数分布直方图(数据分成4组:,,,),以及部分数据信息.
c.这一组的成绩是:
80,80,80,80,81,81,81,83,83,83,84,84,84,85,87.
根据以上信息,回答下列问题:
(1)请补全成绩频数分布表和成绩频数分布直方图;
(2)①直接写出这40名学生中,成绩不低于85分的人数;
②若小明所在年级的200名学生参与此项活动,估计这200名学生中有多少人成绩不低于85分.
21.(2022春·北京东城·七年级统考期末)恩格尔系数是食品支出总额占家庭(或个人)消费或支出总额的比重,常用于反映一个地区人民生活质量的高低,计算公式为:恩格尔系数.对北京市居民家庭1978—2020年的恩格尔系数的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.北京市居民家庭1978—2020年的恩格尔系数的频数分布直方图(数据分成7组:,,,,,,):
b.北京市居民家庭1978—2020年的恩格尔系数在这一组的是:
49.3 49.6 49.7 51.5 52.1 53.6 53.6 53.7
c.北京市居民家庭1978—2020年的恩格尔系数的统计图:
(以上数据来源于《北京统计年鉴(2021)》)
根据以上信息,回答下列问题:
(1)在1978—2020年中,北京市居民家庭的恩格尔系数共有______年低于50%;
(2)北京市居民家庭1978—2020年的恩格尔系数在______年最低(填写年份);
(3)下列推断中合理的是______.
①1988年,北京市居民家庭的食品支出总额约为家庭(或个人)消费或支出总额的一半;
②1978年以来,北京市居民家庭的恩格尔系数总体呈下降趋势,反映了北京市居民的生活质量逐渐提高.
22.(2022春·北京密云·七年级统考期末)随着共享单车的普及,越来越多的居民选择共享单车作为出行的交通工具.为了解某社区居民每周使用共享单车的时间情况,随机对该社区选择共享单车出行的部分居民进行了调研,获得了他们每周使用共享单车时间(单位:小时)的数据,并将收集到的数据进行整理、描述和分析.下面给出了部分信息.
a.该社区居民每周使用共享单车的时间数据的频数分布表如下:
组别 使用时间(小时) 频数(人数)
第1组 5
第2组
第3组 35
第4组
第5组 15
b.该社区居民每周使用共享单车的时间数据的频数分布直方图及扇形图如下:
根据以上信息,回答下列问题:
(1)本次调研,随机抽取_______名社区居民进行调查;
(2)表中m的值为 ,n的值为 ;
(3)第3组居民人数在扇形图中所对应的扇形的圆心角度数是________;
(4)请补全频数分布直方图;
(5)若该社区共有500位居民选择使用共享单车出行,请你估计使用共享单车的时间小于10小时的居民约有________人.
23.(2022春·北京朝阳·七年级统考期末)为了解我国居民生活用水情况,某班数学活动小组对全国省级行政区中的31个进行了调查.通过查阅统计资料,收集了它们2019年和2020年居民人均生活用水量(单位:L/d),并对相关数据进行整理、描述、下面给出了部分信息.
a.2019年和2020年居民人均生活用水量频数分布表:
b.2019年居民人均生活用水量在这一组的是:
120 121 126 127 130 139;
2020年居民人均生活用水量在这一组的是:
123 132 132 135.
c.2019年和2020年居民人均生活用水量统计图:
(说明:有两个省级行政区2019年居民人均生活用水量相同,2020年居民人均生活用水量也相同,都在的范围)
根据以上信息,回答下面问题:
(1)m=______;
(2)在图中,用“○”圈出了代表北京市的点,则北京市2019年居民人均生活用水量为______L/d,北京市2020年居民人均生活用水量为______L/d;
(3)下列推断合理的是______.
①2020年居民人均生活用水量在范围的省级行政区的数量比2019年少;
②2019年居民人均生活用水量在范围的这个省级行政区2020年居民人均生活用水量在0范围.
24.(2022春·北京丰台·七年级统考期末)某学校为了合理地安排学生体育锻炼,需要掌握学生每天课后进行体育锻炼时间的大致情况.在4月份某天随机抽取了若干名学生进行调查,发现被调查的学生当天课后进行体育锻炼的时间都不超过100分钟.现将调查结果绘制成两幅尚不完整的统计图表.
课后体育锻炼时间频数分布表
组别 锻炼时间(分钟) 频数(学生人数) 百分比
12 20%
35%
18
6 10%
3 5%
根据以上信息,回答下列问题:
(1)直接写出本次调查的样本容量,以及频数分布表中,的值;
(2)补全频数分布直方图;
(3)若该校学生共有2200人,估计该校当天课后体育锻炼时间超过60分钟的学生人数.
25.(2022春·北京怀柔·七年级校考期末)小钢同学在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭年收入情况,他从中随机调查了40户居民家庭年收入(单位:万元).对数据(年收入)进行整理、描述和分析.
A.绘制了被抽取的40户居民的家庭年收入的频数分布表和频数分布直方图.
家庭年收入的频数分布表
年收入分钟(万元) 划记 频数
丅 2
正一 6
正 9
3
丅 2
家庭年收入的频数分布直方图
B.家庭年收入在12.5≤x<14.5这一组的是:
12.5 12.5 12.6 12.7 13.0 13.7 13.8.14.1 14.3
根据以上信息,完成下列问题:
(1)将两个统计表(图)补充完整;
(2)估计小钢同学所居住的小区多少户家庭年收入不低于13万元?
参考答案:
1.D
【分析】根据题意和频数分布表、扇形统计图制作的步骤,可以解答本题.
【详解】解:由题可知,正确顺序为②→④→①→③.
故选:D.
【点睛】本题主要考查扇形统计图,折线统计图,掌握统计图的性质是解题的关键.
2.B
【分析】根据全面调查的特点判断A与B;根据样本容量的定义判断C;根据样本具有的特点判断D.
【详解】A、全面调查不能适用于所有的调查,如具有破坏性的抽查只能用抽样调查,故本选项说法错误,不符合题意;
B、为了解全体学生的视力,对每位学生进行视力检查,是全面调查,故本选项说法正确,符合题意;
C、为调查小区1500户家庭用水情况,抽取该小区100户家庭,样本容量为100,故本选项说法错误,不符合题意;
D、为了解全校中学生的身高,不能以该校篮球队队员的身高作为样本,因为篮球队队员的身高普遍较高,这样选取的样本不具有代表性,不能客观估计总体,故本选项说法错误,不符合题意;
故选:B.
【点睛】本题考查了用样本估计总体,全面调查与抽样调查,样本容量,掌握相关概念是解题的关键.
3.B
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:A.了解20万只节能灯的使用寿命,具有破坏性,适合抽样调查,故本选项不合题意;
B.了解某班35名学生的视力情况,人员不多,适合用全面调查,故本选项符合题意;
C.了解某条河流的水质情况,范围广,适合抽样调查,故本选项不合题意;
D.了解全国居民对“垃圾分类”有关内容的认识程度,范围广,适合抽样调查,故本选项不合题意;
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.B
【分析】分析每一个选项的特点,有破坏性的,没有必要的,调查对象特别多的都不适合用普查的方式.
【详解】解:A.调查北京市中学生每周体育锻炼时间,调查对象多且没有必要,不适合普查;
B.调查“神舟十四号”飞船零部件的质量,每一个对象都非常重要,适合普查.
C.调查某一批次的计算器的使用寿命,调查有破坏,不适合用普查;
D.调查全国中学生的视力情况,调查对象多且没有必要,不适合普查;
故选B.
【点睛】本题考查了全面调查或抽样调查,解题的关键是根据一般来说当调查的对象很多又不是每个数据都有很大的意义,或着调查的对象虽然不多,但是带有破坏性,应采用抽查方式;如果调查对象不需要花费太多的时间又不据有破坏性,或者生产生活中有安全隐患,或者意义非常重大等方面的问题就必须采用普查的调查方式进行.
5.A
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:A、了解某地区饮用水矿物质含量的情况,采用抽样调查方式,符合题意;
B、旅客上飞机前的安检,应采用全面调查方式,故此选项不符合题意;
C、对某班学生的校服尺寸大小的调查,应采用全面调查方式,故此选项不符合题意;
D、调查某批次汽车的抗撞击能力,应采用抽样调查方式,故此选项不符合题意.
故选:A.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
6.A
【分析】根据全面调查和抽样调查的定义分析解答.
【详解】解:A、范围小,适合全面调查;
B、范围较大,适合抽样调查,故不符合题意;
C、具有破坏性,适合抽样调查,故不符合题意;
D、范围较大,适合抽样调查,故不符合题意;
故选:A.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
7.D
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似判断即可.
【详解】解:A.对端午节期间市场上粽子质量情况具有破坏性,适合抽样调查,故选项A不符合题意;
B.旅客上飞机前的安检,意义重大,适合全面调查,故选项B不符合题意;
C.调查本市居民对“垃圾分类”有关内容的了解程度工作量大,适合抽样调查,故选项C不符合题意;
D.调查“神舟十一号”飞船重要零部件的产品质量,宜采用全面调查方式,故选项D符合题意;
故选:D.
【点睛】本题考查了抽样调查和全面调查的选择,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
8.C
【分析】折线图是用一个单位表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.
【详解】解:由折线统计图可知,
①年,北京市人均可支配收入逐年增加,故①说法正确;
②年,北京市人均消费支出有所下降,故②原说法错误;
③2019年北京市的人均可支配收入比人均消费支出约多:(元(万元),故③说法正确;
故所有合理推断的序号是①③.
故选:C.
【点睛】本题考查了折线统计图,正确理解折线统计图的意义是解题的关键.
9.C
【分析】根据条形统计图中的数据即可求解.
【详解】解:根据统计图提供的信息得,
A.信息真实性判别表现最好,正确,不符合题意;
B.数字内容创建能力表现最弱,正确,不符合题意;
C.∵专业领域数字化应用能力的平均值为31.2%,数字化协作的平均值为43.8,
∴数字化协作的表现要好于专业领域数字化应用能力的表现,判断不正确,符合题意;
D.平均值高于70%的指标有智能手机应用、信息真实性判别、数字安全意识,正确,不符合题意;
故选:C.
【点睛】此题考查了条形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.
10.B
【分析】根据图像直接判断即可.
【详解】解:由图像可知:用每个季度每斤的售价减去进价可得每斤的利润,第二季度的售价减去进价的差较大,故出售该种水产品每斤利润最大的季度是第二季度,
故选:B.
【点睛】此题考查了函数图像的理解,正确理解函数图像得到相关信息是解题的关键.
11.否,理由是灯泡的使用寿命检查是破坏性试验不适合全面调查
【分析】根据全面调查与抽样调查的定义即可得.
【详解】解:否,理由是灯泡的使用寿命检查是破坏性试验不适合全面调查,
故答案为:否,理由是灯泡的使用寿命检查是破坏性试验不适合全面调查.
【点睛】本题考查了全面调查与抽样调查,选择全面调查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行全面调查、全面调查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用全面调查.
12.108°##108度
【分析】用360°乘“非常清楚”所占比例,即可得出答案.
【详解】解:根据题意得: ,
故答案为:108°.
【点睛】本题考查了用求解扇形图中某部分所对应的圆心角,在扇形统计图中,每部分占整体的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
13.①②
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:下列调查:①调查全市中学生对2022年“中国航天日”主题“航天点亮梦想”的了解情况;②检测某批次节能灯的使用寿命;③选出某体育运动学校速度滑冰成绩最好的学生参加全国比赛.其中适合采用抽样调查的是①②.
故答案为:①②.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
14. 144 240
【分析】用360°乘以B类所占的百分比即可得出圆心角度数;用该校的总人数乘以喜欢D类课程的学生所占的百分比即可.
【详解】解:B类课程对应扇形的圆心角为:360°× =144°.
估计该校1200名学生喜欢D类课程的人数约为1200×=240(人),
故答案为:144,240.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
15.(1)0.3,40
(2)乙
(3)120
【分析】(1)根据各小组的百分比的和是1求解,样本的具体数据除以它所占的百分比得样本容量;
(2)一半以上的百分比就是大于百分之五十;
(3)利用样本的百分比来估计总体的百分比.
(1)
解:;
;
故答案为:0.3,40.
(2)
百分比大于0.5的选图乙,
故答案为:乙.
(3)
(人),
估计成绩在之间的学生人数为120人,
故答案为:120.
【点睛】本题考查了统计中的基本概念的求法,理解它们之间的关系是解题的关键.
16.(1)160;54°
(2)见解析
(3)240
【分析】(1)由D实验内容人数及其所占百分比可得总人数;用360°乘以A人数所占比例即可得出“A”所在扇形的圆心角的度数;
(2)根据四个实验人数和等于总人数求出B对应人数,即可补全图形;
(3)用总人数乘以样本中B实验人数所占比例.
(1)
解:本次调查的总人数为:48÷30%=160(人);
扇形统计图中“A”所在扇形的圆心角的度数为:
故答案为:160;54°.
(2)
B对应人数为:160 24 32 48=56(人),
补全条形统计图如下:
(3)
.
答:本次调查估计该校对水球光学实验最感兴趣的学生人数有240人.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
17.(1)25
(2)108°
(3)见解析
(4)350人
【分析】(1)根据A的百分比乘以总人数,进行计算即可;
(2)求出喜欢体育运动项目C的学生所占的百分比即可;
(3)根据体育项目A、体育项目C的频数补全直方图即可;
(4)用1000乘以总体中喜欢体育项目B的占比进行计算即可.
(1)
(1)100×25%=25(人),
故答案为:25;
(2)
360°×=108°,
答:扇形统计图中“C”对应扇形的圆心角度数为108°;
(3)
喜欢体育项目A的人数为100×25%=25,喜欢体育项目C的人数为100-25-35-10=30(人),
补全统计图如下:
(4)
1000×=350(人),
答:估计全校1000名学生中最喜欢B运动项目的人数约为350人.
本题考查的是条形统计图和扇形统计图的综合运用,样本估计总体,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
18.(1),
(2)750人
【分析】(1)根据B组所占百分比及B组人数可以求出总人数,再根据A组百分比求出a的值,最后用减法求出b的值;
(2)先计算抽查人数中每天阅读时长在的人数所占百分比,再根据该校七年级的学生总数估计该校七年级学生每天阅读时长在0.5<x≤1.5的人数.
(1)
∵72÷60%=120,
∴a=120×20%=24,b=120-(24+72+18)=6;
(2)
(人),
答:估计该校七年级学生每天阅读时长在的共有750人.
【点睛】本题考查数据的整理与分析,熟练掌握扇形统计图的有关计算与运用样本估计总体的方法是解题关键.
19.(1)图见解析
(2)春风,12,秋风
(3)①③
【分析】(1)根据频数统计表补全条形统计图即可;
(2)分别找出统计表中李白和杜甫的最大数即可得李白和杜甫最常使用的词语,再利用896除以李白最常使用的词语的频数即可得;
(3)根据杜甫和李白与“风”有关的词语的频率即可判断①;根据个性化用字词云图即可判断②;在与“风”相关的词语中,找出李白和杜甫最常使用的词语,再根据相关词语的寓意即可判断③.
【详解】(1)解:根据频数统计表补全条形统计图如下:
(2)解:李白:在与“风”相关的词语中,春风出现的次数最多,为72次,
所以在与“风”相关的词语中,李白最常使用的词语是春风,
,
则在李白的诗歌作品中,大约每12首诗歌中就会出现一次春风;
杜甫:在与“风”相关的词语中,秋风出现的次数最多,为30次,
所以在与“风”相关的词语中,杜甫最常使用的词语是秋风,
故答案为:春风,12,秋风.
(3)解:与“风”有关的词语在李白的诗歌中出现的总频数为,
则频率为
与“风”有关的词语在杜甫的诗歌中出现的总频数为,
则频率为
则相较于杜甫,与“风”有关的词语在李白的诗歌中更常见,推断①合理;
由个性化用字词云图可知,李白最常使用的汉字是“歌”,杜甫则是“江”,则推断②不合理;
根据条形图,可知:
李白更常用“风”是“春风”,“清风”,表达喜悦,而杜甫更常用“风”是“秋风”表达悲伤,
则③合理;
故答案为:①③.
【点睛】本题考查了条形统计图、统计表等知识点,熟练掌握统计调查的相关知识是解题关键.
20.(1)见解析
(2)①9人;②45人
【分析】(1)结合表格和直方图可得答案;
(2)①根据表格中的数据即可得出答案;
②用总人数乘以样本中成绩不低于85分的人数所占比例即可.
(1)
解:由题意知,60≤x<70的人数为6,70≤x<80的人数为12,80≤x<90的人数为15,90≤x<100的人数为7,
补全表格和图形如下:
成绩 频数
60≤x<70 6
70≤x<80 12
80≤x<90 15
90≤x<100 7
(2)
①成绩不低于85分的人数为2+7=9(人);
②200×=45(人),
答:估计这200名学生中有45人成绩不低于85分.
【点睛】本题考查频数分布表、频数分布直方图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
21.(1)31;
(2)2019;
(3)②.
【分析】(1)根据频数分布直方图中的数据得出恩格尔系数小于50%的频数即可;
(2)根据北京市居民家庭1978-2020年的恩格尔系数的折线统计图找出最低点所对应的年份即可;
(3)根据恩格尔系数结合具体的统计图进行判断即可.
(1)
在1978一2020年中,北京市居民家庭的恩格尔系数低于50%的频数为9+9+3+2+5+3=31(年),
故答案为:31;
(2)
北京市居民家庭1978-2020年的恩格尔系数的折线统计图中最低点所对应的年份是2019年,
故答案为:2019;
(3)
①从北京市居民家庭1978-2020年的恩格尔系数的折线统计图中,1988年北京市居民家庭的食品支出总额约为家庭(或个人)消费或支出总额的一半以上,约为55%,因此①不正确;
②1978年以来,北京市居民家庭的恩格尔系数总体呈下降趋势,反映了北京市居民的生活质量逐渐提高.是正确的;
故答案为:②.
【点睛】本题考查折线统计图、频数分布直方图以及样本估计总体,理解恩格尔系数的定义是正确判断的前提.
22.(1)100
(2),
(3)126°
(4)见解析
(5)325
【分析】(1)用第5组的频数除以15%计算即可;
(2)根据频数分布直方图可得n的值,再用总人数分别减去其它组人数即可得出m的值;
(3)用360°乘第3组所占比例即可;
(4)根据m的值即可补全频数分布直方图;
(5)用样本估计总体的思想即解决问题;
【详解】(1)解:15÷15%=100(人),
即本次调研,随机抽取100名社区居民进行调查,
故答案为:100;
(2)解:由题意可知n=20,
∴m=100﹣5﹣35﹣20﹣15=25,
故答案为:25;20;
(3)解:第3组居民人数在扇形图中所对应的扇形的圆心角度数是360°×=126°,
故答案为:126°;
(4)解:补全频数分布直方图如下:
(5)解:500×=325(人),
∴估计使用共享单车的时间小于10小时的居民约有325人.
故答案为:325.
【点睛】本题考查频数发布直方图、扇形统计图、样本估计总体的思想等知识,解题的关键是掌握基本概念.
23.(1)5
(2)139,135
(3)①②
【分析】(1)根据调查总数减去其他组的频数即可求解;
(2)根据2019年和2020年居民人均生活用水量统计图以及题目的点信息找到对应点解答即可;
(3)根据题意,结合图形分析解答.
(1)
解:,
故答案为:5;
(2)
由年和2020年居民人均生活用水量统计图以及信息得:
北京市2019年居民人均生活用水量为,北京市2020年居民人均生活用水量为,
故答案为:139,135;
(3)
根据题意得,
①2020年居民人均生活用水量在范围的省级行政区有3个,2019年居民人均生活用水量在范围的省级行政区有4个,
年居民人均生活用水量在范围的省级行政区的数量比2019年少,
推断①合理;
②由年和2020年居民人均生活用水量统计图得:
2019年居民人均生活用水量在范围的这个省级行政区2020年居民人均生活用水量在范围.
推断②合理;
故答案为:①②.
【点睛】本题主要考查了统计图的识别与应用,关键是正确识别统计图.
24.(1)60,21,30%;
(2)画图见解析
(3)该校每天课后进行体育锻炼的时间超过60分钟的学生共有330人.
【分析】(1)由A的人数除以所占百分比求出样本容量,进而求出a,b的值,即可解决问题;
(2)将频数分布直方图补充完整即可;
(3)由该校学生总人数乘以每天课后进行体育锻炼的时间超过60分钟的学生所占的百分比即可.
(1)
解:本次调查的样本容量是:12÷20%=60,
则a=60-12-18-6-3=21,b=18÷60×100%=30%,
故答案为:60,21,30%;
(2)
将频数分布直方图补充完整如下:
(3)
2200×(10%+5%)=330(人),
即该校每天课后进行体育锻炼的时间超过60分钟的学生共有330人.
【点睛】本题考查的是频数分布表与频数分布直方图,补全频数分布直方图,利用样本估计总体,掌握以上基础的统计知识是解本题的关键.
25.(1)见解析
(2)估计小钢同学所居住的小区110户家庭年收入不低于13万元
【分析】(1)先求出:年收入在的户数,然后补全统计图和统计表即可;
(2)用440乘以样本中年收入不低于13万元的户数占比即可.
【详解】(1)解:年收入在的户数为(户),
∴补全统计图(表)如下:
年收入分钟(万元) 划记 频数
丅 2
正一 6
正正正 18
正 9
3
丅 2
(2)解:户,
∴估计小钢同学所居住的小区110户家庭年收入不低于13万元.
【点睛】本题主要考查了频数分布表,频数分布直方图,用样本估计总体,正确读懂统计图是解题的关键.
一、单选题
1.(2022春·北京延庆·七年级统考期末)某同学要调查、分析本校七年级(1)班学生的身高状况,作为三年中跟踪调查的依据.
以下是排乱的统计步骤:
①绘制扇形统计图来表示各个身高范围所占的百分比;
②去校医务室收集学生入学后体检的有关数据;
③从扇形统计图中分析出学生身高状况;
④整理收集的相关数据,并按身高范围进行分组,在表格中表示出来.
正确统计步骤的顺序是( )
A.②→③→①→④ B.③→④→①→②
C.①→②→④→③ D.②→④→①→③
2.(2022春·北京东城·七年级统考期末)在以下四个有关统计调查的说法中,正确的是( )
A.全面调查适用于所有的调查
B.为了解全体学生的视力,对每位学生进行视力检查,是全面调查
C.为调查小区1500户家庭用水情况,抽取该小区100户家庭,样本容量为1500
D.为了解全校中学生的身高,以该校篮球队队员的身高作为样本,能客观估计总体
3.(2022春·北京昌平·七年级统考期末)下列调查中,适合用全面调查的是( )
A.了解20万只节能灯的使用寿命 B.了解某班35名学生的视力情况
C.了解某条河流的水质情况 D.了解全国居民对“垃圾分类”有关内容的认识程度
4.(2022春·北京延庆·七年级统考期末)下列调查方式,适合全面调查的是( )
A.调查北京市中学生每周体育锻炼时间 B.调查神舟十四号飞船零部件的质量
C.调查某一批次的计算器的使用寿命 D.调查全国中学生的视力情况
5.(2022春·北京丰台·七年级统考期末)下列调查方式,你认为最合适的是( )
A.对某地区饮用水矿物质含量的调查,采用抽样调查方式
B.旅客上飞机前的安全检查,采用抽样调查方式
C.对某班学生的校服尺寸大小的调查,采用抽样调查方式
D.调查某批次汽车的抗撞击能力,采用全面调查方式
6.(2022春·北京怀柔·七年级校考期末)下列调查活动,适合使用全面调查的是( )
A.调查某班同学课外体育锻炼时间; B.调查全市植树节中栽植树苗的成活率;
C.调查某种品牌照明灯的使用寿命; D.调查抗美援朝纪录片《为了和平》在线收视率.
7.(2022春·北京通州·七年级统考期末)下列调查方式,你认为最合适的是( )
A.对端午节期间市场上粽子质量情况,采用全面调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C.调查本市居民对“垃圾分类”有关内容的了解程度,采用全面调查方式
D.调查“神舟十一号”飞船重要零部件的产品质量,采用全面调查方式
8.(2022春·北京朝阳·七年级统考期末)下面的统计图反映了2013-2020年北京市人均可支配收入和人均消费支出的情况.
根据统计图提供的信息,下面有三个推断:
①2013-2020年,北京市人均可支配收入逐年增加;
②2013-2020年,北京市人均消费支出逐年增加;
③2019年北京市的人均可支配收入比人均消费支出约多2.47万元.
其中所有合理推断的序号是( )
A.① B.②③ C.①③ D.①②③
9.(2022春·北京西城·七年级统考期末)在《2016-2021年中国公民数字素养研究报告》中,中国社会科学院信息化研究中心课题组对我国城市居民的数字素养展开评估.下面是根据我国城市居民的11项数字素养平均值制作的统计图.
根据统计图提供的信息,下面关于我国城市居民数字素养指标的判断不正确的是( )
A.信息真实性判别表现最好
B.数字内容创建能力表现最弱
C.专业领域数字化应用能力的表现要好于数字化协作的表现
D.平均值高于70%的指标有智能手机应用、信息真实性判别、数字安全意识
10.(2022春·北京密云·七年级统考期末)在一年的四个季度中,某种水产品的每斤进价与售价的信息如图所示,则出售该种水产品每斤利润最大的季度是( )
A.第一季度 B.第二季度 C.第三季度 D.第四季度
二、填空题
11.(2022春·北京海淀·七年级统考期末)如图是一家灯泡生产厂商的广告图,请从统计学角度判断广告语是否合适,并说明理由:_____________________
12.(2022春·北京丰台·七年级统考期末)某学校为调查学生对《中华人民共和国未成年人保护法》了解的情况,随机抽取部分学生进行调查,并将调查结果绘制成扇形统计图.如图,对该法“非常清楚”的学生对应扇形的圆心角度数为______.
13.(2022春·北京朝阳·七年级统考期末)下列调查:①调查全市中学生对2022年“中国航天日”主题“航天点亮梦想”的了解情况;②检测某批次节能灯的使用寿命;③选出某体育运动学校速度滑冰成绩最好的学生参加全国比赛,其中适合采用抽样调查的是______(写出所有正确答案的序号).
14.(2022春·北京顺义·七年级统考期末)某校利用课后服务时间,开设了A,B,C,D,E五类课程.某小组利用课余时间从全校1200名学生中抽取50名学生进行了“你最喜爱的课程”的抽样调查(每个被调查的学生必须选择而且只能选择其中一项),并将调查结果绘制成如下统计图:
则图2中B类课程对应扇形的圆心角为_______°,估计该校1200名学生喜欢D类课程的人数约为_______.
三、解答题
15.(2022春·北京朝阳·七年级统考期末)某校组织全体学生参加“网络安全知识”竞赛,为了解学生们在本次竞赛中的成绩x(百分制),进行了抽样调查,所画统计图如下.
根据以上信息,回答下列问题:
(1)m=______%,样本容量为______;
(2)能更好地说明样本中一半以上学生的成绩在之间的统计图是______(填“甲”或“乙”);
(3)如果该校共有学生400人,估计成绩在之间的学生人数为______.
16.(2022春·北京大兴·七年级统考期末)2021年12月9日15时40分,“天宫课堂”第一课开讲.神舟十三号乘组航天员翟志刚、王亚平、叶光富3名航天员演示微重力环境下细胞实验、物体运动、液体表面张力等现象,并讲解了实验背后的科学原理,课堂中展示了四个实验:A.浮力消失实验B.水膜张力实验C.水球光学实验D.泡腾片实验,某校为了解学生们在这四个实验中最感兴趣的一个(每位同学必须从中选择一项且只能选择一项),随机抽取了部分同学,并绘制了以下两幅不完整的统计图,如图所示:
(1)本次调查的总人数为______人,扇形统计图中“A”所在扇形的圆心角的度数为______;
(2)请补全条形统计图;
(3)若该校共有1200名同学,请根据抽样调查数据估计该校同学中对“水球光学实验”最感兴趣的人数.
17.(2022春·北京石景山·七年级统考期末)某学校体育兴趣小组,为了更好的开展活动,需要了解学校1000名学生对A,B,C,D四项体育活动的喜好情况,随机抽取了100名学生进行了“你最喜欢哪种运动”的调查(必选且只选一种),根据调查绘制了条形统计图和扇形统计图,部分信息如下:
(1)在抽取的100人中最喜欢运动项目A的人数为 ;
(2)求扇形统计图中“C”对应扇形的圆心角度数;
(3)补全条形统计图;
(4)依据本次调查结果,估计全校1000人名学生中最喜欢B运动项目的人数.
18.(2022春·北京延庆·七年级统考期末)某区图书馆充分发挥数字教育资源优势,利用“数字图书馆”组织开展了主题为“居家数字阅读+悦读”的中小学生寒假阅读主题活动.某校随机抽取了七年级的若干学生进行调查,并将所收集的数据分组整理,绘制了如下两幅不完整的统计图表,请根据图表信息回答下列问题.
七年级学生每天阅读时长情况统计表
组别 阅读时长(单位:小时) 人数(单位:人)
A 0<x≤0.5
B 0.5<x≤1 72
C 1<x≤1.5 18
D 1.5<x≤2
根据以上信息,回答下列问题:
(1)求出表中a,b的值;
(2)已知该校七年级的学生有1000人,试估计该校七年级学生每天阅读时长在0.5<x≤1.5的共有多少人?
19.(2022春·北京海淀·七年级统考期末)清朝康熙年间编校的《全唐诗》包含四万多首诗歌,逾三百万字,是后人研究唐诗的重要资源.小云利用统计知识分析《全唐诗》中李白和杜甫作品的风格差异.下面给出了部分信息:
a.《全唐诗》中,李白和杜甫分别有896和1158首作品.
b.二人作品中与“风”相关的词语频数统计表如下:
词语 频 数 诗人 春风 东风 清风 悲风 秋风 北风
李白 72 24 28 6 26 8
杜甫 19 4 6 10 30 14
c.通过统计二人的个性化用字,可绘制一种视觉效果更强的“词云图”,出现次数较多的关键字被予以视觉上的突出.
注:在文学作品中,东风即春风,常含有生机勃勃之意和喜春之情,如:等闲识得东风面,万紫千红总是春;北风通常寄寓诗人凄苦的情怀,抒写伤别之情,如:千里黄云白日曛,北风吹雁雪纷纷.
根据以上信息,回答下列问题:
(1)补全条形统计图:
(2)在与“风”相关的词语中,李白最常使用的词语是________,大约每________首诗歌中就会出现一次该词语(结果取整数),而杜甫最常使用的词语是________;
(3)下列推断合理的是________.
①相较于杜甫,与“风”有关的词语在李白的诗歌中更常见;
②个性化用字中,李白最常使用的汉字是“水”,杜甫则是“江”;
③李白更常用“风”表达喜悦,而杜甫更常用“风”表达悲伤.
20.(2022春·北京西城·七年级统考期末)故宫博物院为鼓励游客参与“故宫零废弃”项目做好垃圾分类,在“数字故宫”小程序中推出了一项体验活动,将故宫改造升级后的垃圾桶编号并精心布局,在每个垃圾桶点位(共79个)设置一道与院内场景相关的篆体古字题目,游客点击相应点位的垃圾桶编号解答题目,以形会意,看字识“物”,并在感受中国传统文化的同时,了解垃圾分类知识.
王老师在全年级随机邀请了40名学生在线参与答题,小明所在小组收集、整理同学们看字识“物”和辨别垃圾的答题成绩并制作统计图表(成绩设为百分制).下面是这40名学生成绩的频数分布表、频数分布直方图(数据分成4组:,,,),以及部分数据信息.
c.这一组的成绩是:
80,80,80,80,81,81,81,83,83,83,84,84,84,85,87.
根据以上信息,回答下列问题:
(1)请补全成绩频数分布表和成绩频数分布直方图;
(2)①直接写出这40名学生中,成绩不低于85分的人数;
②若小明所在年级的200名学生参与此项活动,估计这200名学生中有多少人成绩不低于85分.
21.(2022春·北京东城·七年级统考期末)恩格尔系数是食品支出总额占家庭(或个人)消费或支出总额的比重,常用于反映一个地区人民生活质量的高低,计算公式为:恩格尔系数.对北京市居民家庭1978—2020年的恩格尔系数的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
a.北京市居民家庭1978—2020年的恩格尔系数的频数分布直方图(数据分成7组:,,,,,,):
b.北京市居民家庭1978—2020年的恩格尔系数在这一组的是:
49.3 49.6 49.7 51.5 52.1 53.6 53.6 53.7
c.北京市居民家庭1978—2020年的恩格尔系数的统计图:
(以上数据来源于《北京统计年鉴(2021)》)
根据以上信息,回答下列问题:
(1)在1978—2020年中,北京市居民家庭的恩格尔系数共有______年低于50%;
(2)北京市居民家庭1978—2020年的恩格尔系数在______年最低(填写年份);
(3)下列推断中合理的是______.
①1988年,北京市居民家庭的食品支出总额约为家庭(或个人)消费或支出总额的一半;
②1978年以来,北京市居民家庭的恩格尔系数总体呈下降趋势,反映了北京市居民的生活质量逐渐提高.
22.(2022春·北京密云·七年级统考期末)随着共享单车的普及,越来越多的居民选择共享单车作为出行的交通工具.为了解某社区居民每周使用共享单车的时间情况,随机对该社区选择共享单车出行的部分居民进行了调研,获得了他们每周使用共享单车时间(单位:小时)的数据,并将收集到的数据进行整理、描述和分析.下面给出了部分信息.
a.该社区居民每周使用共享单车的时间数据的频数分布表如下:
组别 使用时间(小时) 频数(人数)
第1组 5
第2组
第3组 35
第4组
第5组 15
b.该社区居民每周使用共享单车的时间数据的频数分布直方图及扇形图如下:
根据以上信息,回答下列问题:
(1)本次调研,随机抽取_______名社区居民进行调查;
(2)表中m的值为 ,n的值为 ;
(3)第3组居民人数在扇形图中所对应的扇形的圆心角度数是________;
(4)请补全频数分布直方图;
(5)若该社区共有500位居民选择使用共享单车出行,请你估计使用共享单车的时间小于10小时的居民约有________人.
23.(2022春·北京朝阳·七年级统考期末)为了解我国居民生活用水情况,某班数学活动小组对全国省级行政区中的31个进行了调查.通过查阅统计资料,收集了它们2019年和2020年居民人均生活用水量(单位:L/d),并对相关数据进行整理、描述、下面给出了部分信息.
a.2019年和2020年居民人均生活用水量频数分布表:
b.2019年居民人均生活用水量在这一组的是:
120 121 126 127 130 139;
2020年居民人均生活用水量在这一组的是:
123 132 132 135.
c.2019年和2020年居民人均生活用水量统计图:
(说明:有两个省级行政区2019年居民人均生活用水量相同,2020年居民人均生活用水量也相同,都在的范围)
根据以上信息,回答下面问题:
(1)m=______;
(2)在图中,用“○”圈出了代表北京市的点,则北京市2019年居民人均生活用水量为______L/d,北京市2020年居民人均生活用水量为______L/d;
(3)下列推断合理的是______.
①2020年居民人均生活用水量在范围的省级行政区的数量比2019年少;
②2019年居民人均生活用水量在范围的这个省级行政区2020年居民人均生活用水量在0范围.
24.(2022春·北京丰台·七年级统考期末)某学校为了合理地安排学生体育锻炼,需要掌握学生每天课后进行体育锻炼时间的大致情况.在4月份某天随机抽取了若干名学生进行调查,发现被调查的学生当天课后进行体育锻炼的时间都不超过100分钟.现将调查结果绘制成两幅尚不完整的统计图表.
课后体育锻炼时间频数分布表
组别 锻炼时间(分钟) 频数(学生人数) 百分比
12 20%
35%
18
6 10%
3 5%
根据以上信息,回答下列问题:
(1)直接写出本次调查的样本容量,以及频数分布表中,的值;
(2)补全频数分布直方图;
(3)若该校学生共有2200人,估计该校当天课后体育锻炼时间超过60分钟的学生人数.
25.(2022春·北京怀柔·七年级校考期末)小钢同学在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭年收入情况,他从中随机调查了40户居民家庭年收入(单位:万元).对数据(年收入)进行整理、描述和分析.
A.绘制了被抽取的40户居民的家庭年收入的频数分布表和频数分布直方图.
家庭年收入的频数分布表
年收入分钟(万元) 划记 频数
丅 2
正一 6
正 9
3
丅 2
家庭年收入的频数分布直方图
B.家庭年收入在12.5≤x<14.5这一组的是:
12.5 12.5 12.6 12.7 13.0 13.7 13.8.14.1 14.3
根据以上信息,完成下列问题:
(1)将两个统计表(图)补充完整;
(2)估计小钢同学所居住的小区多少户家庭年收入不低于13万元?
参考答案:
1.D
【分析】根据题意和频数分布表、扇形统计图制作的步骤,可以解答本题.
【详解】解:由题可知,正确顺序为②→④→①→③.
故选:D.
【点睛】本题主要考查扇形统计图,折线统计图,掌握统计图的性质是解题的关键.
2.B
【分析】根据全面调查的特点判断A与B;根据样本容量的定义判断C;根据样本具有的特点判断D.
【详解】A、全面调查不能适用于所有的调查,如具有破坏性的抽查只能用抽样调查,故本选项说法错误,不符合题意;
B、为了解全体学生的视力,对每位学生进行视力检查,是全面调查,故本选项说法正确,符合题意;
C、为调查小区1500户家庭用水情况,抽取该小区100户家庭,样本容量为100,故本选项说法错误,不符合题意;
D、为了解全校中学生的身高,不能以该校篮球队队员的身高作为样本,因为篮球队队员的身高普遍较高,这样选取的样本不具有代表性,不能客观估计总体,故本选项说法错误,不符合题意;
故选:B.
【点睛】本题考查了用样本估计总体,全面调查与抽样调查,样本容量,掌握相关概念是解题的关键.
3.B
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:A.了解20万只节能灯的使用寿命,具有破坏性,适合抽样调查,故本选项不合题意;
B.了解某班35名学生的视力情况,人员不多,适合用全面调查,故本选项符合题意;
C.了解某条河流的水质情况,范围广,适合抽样调查,故本选项不合题意;
D.了解全国居民对“垃圾分类”有关内容的认识程度,范围广,适合抽样调查,故本选项不合题意;
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.B
【分析】分析每一个选项的特点,有破坏性的,没有必要的,调查对象特别多的都不适合用普查的方式.
【详解】解:A.调查北京市中学生每周体育锻炼时间,调查对象多且没有必要,不适合普查;
B.调查“神舟十四号”飞船零部件的质量,每一个对象都非常重要,适合普查.
C.调查某一批次的计算器的使用寿命,调查有破坏,不适合用普查;
D.调查全国中学生的视力情况,调查对象多且没有必要,不适合普查;
故选B.
【点睛】本题考查了全面调查或抽样调查,解题的关键是根据一般来说当调查的对象很多又不是每个数据都有很大的意义,或着调查的对象虽然不多,但是带有破坏性,应采用抽查方式;如果调查对象不需要花费太多的时间又不据有破坏性,或者生产生活中有安全隐患,或者意义非常重大等方面的问题就必须采用普查的调查方式进行.
5.A
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:A、了解某地区饮用水矿物质含量的情况,采用抽样调查方式,符合题意;
B、旅客上飞机前的安检,应采用全面调查方式,故此选项不符合题意;
C、对某班学生的校服尺寸大小的调查,应采用全面调查方式,故此选项不符合题意;
D、调查某批次汽车的抗撞击能力,应采用抽样调查方式,故此选项不符合题意.
故选:A.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
6.A
【分析】根据全面调查和抽样调查的定义分析解答.
【详解】解:A、范围小,适合全面调查;
B、范围较大,适合抽样调查,故不符合题意;
C、具有破坏性,适合抽样调查,故不符合题意;
D、范围较大,适合抽样调查,故不符合题意;
故选:A.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
7.D
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似判断即可.
【详解】解:A.对端午节期间市场上粽子质量情况具有破坏性,适合抽样调查,故选项A不符合题意;
B.旅客上飞机前的安检,意义重大,适合全面调查,故选项B不符合题意;
C.调查本市居民对“垃圾分类”有关内容的了解程度工作量大,适合抽样调查,故选项C不符合题意;
D.调查“神舟十一号”飞船重要零部件的产品质量,宜采用全面调查方式,故选项D符合题意;
故选:D.
【点睛】本题考查了抽样调查和全面调查的选择,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
8.C
【分析】折线图是用一个单位表示一定的数量,根据数量的多少描出各点,然后把各点用线段依次连接起来.以折线的上升或下降来表示统计数量增减变化.
【详解】解:由折线统计图可知,
①年,北京市人均可支配收入逐年增加,故①说法正确;
②年,北京市人均消费支出有所下降,故②原说法错误;
③2019年北京市的人均可支配收入比人均消费支出约多:(元(万元),故③说法正确;
故所有合理推断的序号是①③.
故选:C.
【点睛】本题考查了折线统计图,正确理解折线统计图的意义是解题的关键.
9.C
【分析】根据条形统计图中的数据即可求解.
【详解】解:根据统计图提供的信息得,
A.信息真实性判别表现最好,正确,不符合题意;
B.数字内容创建能力表现最弱,正确,不符合题意;
C.∵专业领域数字化应用能力的平均值为31.2%,数字化协作的平均值为43.8,
∴数字化协作的表现要好于专业领域数字化应用能力的表现,判断不正确,符合题意;
D.平均值高于70%的指标有智能手机应用、信息真实性判别、数字安全意识,正确,不符合题意;
故选:C.
【点睛】此题考查了条形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.
10.B
【分析】根据图像直接判断即可.
【详解】解:由图像可知:用每个季度每斤的售价减去进价可得每斤的利润,第二季度的售价减去进价的差较大,故出售该种水产品每斤利润最大的季度是第二季度,
故选:B.
【点睛】此题考查了函数图像的理解,正确理解函数图像得到相关信息是解题的关键.
11.否,理由是灯泡的使用寿命检查是破坏性试验不适合全面调查
【分析】根据全面调查与抽样调查的定义即可得.
【详解】解:否,理由是灯泡的使用寿命检查是破坏性试验不适合全面调查,
故答案为:否,理由是灯泡的使用寿命检查是破坏性试验不适合全面调查.
【点睛】本题考查了全面调查与抽样调查,选择全面调查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行全面调查、全面调查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用全面调查.
12.108°##108度
【分析】用360°乘“非常清楚”所占比例,即可得出答案.
【详解】解:根据题意得: ,
故答案为:108°.
【点睛】本题考查了用求解扇形图中某部分所对应的圆心角,在扇形统计图中,每部分占整体的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
13.①②
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【详解】解:下列调查:①调查全市中学生对2022年“中国航天日”主题“航天点亮梦想”的了解情况;②检测某批次节能灯的使用寿命;③选出某体育运动学校速度滑冰成绩最好的学生参加全国比赛.其中适合采用抽样调查的是①②.
故答案为:①②.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
14. 144 240
【分析】用360°乘以B类所占的百分比即可得出圆心角度数;用该校的总人数乘以喜欢D类课程的学生所占的百分比即可.
【详解】解:B类课程对应扇形的圆心角为:360°× =144°.
估计该校1200名学生喜欢D类课程的人数约为1200×=240(人),
故答案为:144,240.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
15.(1)0.3,40
(2)乙
(3)120
【分析】(1)根据各小组的百分比的和是1求解,样本的具体数据除以它所占的百分比得样本容量;
(2)一半以上的百分比就是大于百分之五十;
(3)利用样本的百分比来估计总体的百分比.
(1)
解:;
;
故答案为:0.3,40.
(2)
百分比大于0.5的选图乙,
故答案为:乙.
(3)
(人),
估计成绩在之间的学生人数为120人,
故答案为:120.
【点睛】本题考查了统计中的基本概念的求法,理解它们之间的关系是解题的关键.
16.(1)160;54°
(2)见解析
(3)240
【分析】(1)由D实验内容人数及其所占百分比可得总人数;用360°乘以A人数所占比例即可得出“A”所在扇形的圆心角的度数;
(2)根据四个实验人数和等于总人数求出B对应人数,即可补全图形;
(3)用总人数乘以样本中B实验人数所占比例.
(1)
解:本次调查的总人数为:48÷30%=160(人);
扇形统计图中“A”所在扇形的圆心角的度数为:
故答案为:160;54°.
(2)
B对应人数为:160 24 32 48=56(人),
补全条形统计图如下:
(3)
.
答:本次调查估计该校对水球光学实验最感兴趣的学生人数有240人.
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
17.(1)25
(2)108°
(3)见解析
(4)350人
【分析】(1)根据A的百分比乘以总人数,进行计算即可;
(2)求出喜欢体育运动项目C的学生所占的百分比即可;
(3)根据体育项目A、体育项目C的频数补全直方图即可;
(4)用1000乘以总体中喜欢体育项目B的占比进行计算即可.
(1)
(1)100×25%=25(人),
故答案为:25;
(2)
360°×=108°,
答:扇形统计图中“C”对应扇形的圆心角度数为108°;
(3)
喜欢体育项目A的人数为100×25%=25,喜欢体育项目C的人数为100-25-35-10=30(人),
补全统计图如下:
(4)
1000×=350(人),
答:估计全校1000名学生中最喜欢B运动项目的人数约为350人.
本题考查的是条形统计图和扇形统计图的综合运用,样本估计总体,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
18.(1),
(2)750人
【分析】(1)根据B组所占百分比及B组人数可以求出总人数,再根据A组百分比求出a的值,最后用减法求出b的值;
(2)先计算抽查人数中每天阅读时长在的人数所占百分比,再根据该校七年级的学生总数估计该校七年级学生每天阅读时长在0.5<x≤1.5的人数.
(1)
∵72÷60%=120,
∴a=120×20%=24,b=120-(24+72+18)=6;
(2)
(人),
答:估计该校七年级学生每天阅读时长在的共有750人.
【点睛】本题考查数据的整理与分析,熟练掌握扇形统计图的有关计算与运用样本估计总体的方法是解题关键.
19.(1)图见解析
(2)春风,12,秋风
(3)①③
【分析】(1)根据频数统计表补全条形统计图即可;
(2)分别找出统计表中李白和杜甫的最大数即可得李白和杜甫最常使用的词语,再利用896除以李白最常使用的词语的频数即可得;
(3)根据杜甫和李白与“风”有关的词语的频率即可判断①;根据个性化用字词云图即可判断②;在与“风”相关的词语中,找出李白和杜甫最常使用的词语,再根据相关词语的寓意即可判断③.
【详解】(1)解:根据频数统计表补全条形统计图如下:
(2)解:李白:在与“风”相关的词语中,春风出现的次数最多,为72次,
所以在与“风”相关的词语中,李白最常使用的词语是春风,
,
则在李白的诗歌作品中,大约每12首诗歌中就会出现一次春风;
杜甫:在与“风”相关的词语中,秋风出现的次数最多,为30次,
所以在与“风”相关的词语中,杜甫最常使用的词语是秋风,
故答案为:春风,12,秋风.
(3)解:与“风”有关的词语在李白的诗歌中出现的总频数为,
则频率为
与“风”有关的词语在杜甫的诗歌中出现的总频数为,
则频率为
则相较于杜甫,与“风”有关的词语在李白的诗歌中更常见,推断①合理;
由个性化用字词云图可知,李白最常使用的汉字是“歌”,杜甫则是“江”,则推断②不合理;
根据条形图,可知:
李白更常用“风”是“春风”,“清风”,表达喜悦,而杜甫更常用“风”是“秋风”表达悲伤,
则③合理;
故答案为:①③.
【点睛】本题考查了条形统计图、统计表等知识点,熟练掌握统计调查的相关知识是解题关键.
20.(1)见解析
(2)①9人;②45人
【分析】(1)结合表格和直方图可得答案;
(2)①根据表格中的数据即可得出答案;
②用总人数乘以样本中成绩不低于85分的人数所占比例即可.
(1)
解:由题意知,60≤x<70的人数为6,70≤x<80的人数为12,80≤x<90的人数为15,90≤x<100的人数为7,
补全表格和图形如下:
成绩 频数
60≤x<70 6
70≤x<80 12
80≤x<90 15
90≤x<100 7
(2)
①成绩不低于85分的人数为2+7=9(人);
②200×=45(人),
答:估计这200名学生中有45人成绩不低于85分.
【点睛】本题考查频数分布表、频数分布直方图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
21.(1)31;
(2)2019;
(3)②.
【分析】(1)根据频数分布直方图中的数据得出恩格尔系数小于50%的频数即可;
(2)根据北京市居民家庭1978-2020年的恩格尔系数的折线统计图找出最低点所对应的年份即可;
(3)根据恩格尔系数结合具体的统计图进行判断即可.
(1)
在1978一2020年中,北京市居民家庭的恩格尔系数低于50%的频数为9+9+3+2+5+3=31(年),
故答案为:31;
(2)
北京市居民家庭1978-2020年的恩格尔系数的折线统计图中最低点所对应的年份是2019年,
故答案为:2019;
(3)
①从北京市居民家庭1978-2020年的恩格尔系数的折线统计图中,1988年北京市居民家庭的食品支出总额约为家庭(或个人)消费或支出总额的一半以上,约为55%,因此①不正确;
②1978年以来,北京市居民家庭的恩格尔系数总体呈下降趋势,反映了北京市居民的生活质量逐渐提高.是正确的;
故答案为:②.
【点睛】本题考查折线统计图、频数分布直方图以及样本估计总体,理解恩格尔系数的定义是正确判断的前提.
22.(1)100
(2),
(3)126°
(4)见解析
(5)325
【分析】(1)用第5组的频数除以15%计算即可;
(2)根据频数分布直方图可得n的值,再用总人数分别减去其它组人数即可得出m的值;
(3)用360°乘第3组所占比例即可;
(4)根据m的值即可补全频数分布直方图;
(5)用样本估计总体的思想即解决问题;
【详解】(1)解:15÷15%=100(人),
即本次调研,随机抽取100名社区居民进行调查,
故答案为:100;
(2)解:由题意可知n=20,
∴m=100﹣5﹣35﹣20﹣15=25,
故答案为:25;20;
(3)解:第3组居民人数在扇形图中所对应的扇形的圆心角度数是360°×=126°,
故答案为:126°;
(4)解:补全频数分布直方图如下:
(5)解:500×=325(人),
∴估计使用共享单车的时间小于10小时的居民约有325人.
故答案为:325.
【点睛】本题考查频数发布直方图、扇形统计图、样本估计总体的思想等知识,解题的关键是掌握基本概念.
23.(1)5
(2)139,135
(3)①②
【分析】(1)根据调查总数减去其他组的频数即可求解;
(2)根据2019年和2020年居民人均生活用水量统计图以及题目的点信息找到对应点解答即可;
(3)根据题意,结合图形分析解答.
(1)
解:,
故答案为:5;
(2)
由年和2020年居民人均生活用水量统计图以及信息得:
北京市2019年居民人均生活用水量为,北京市2020年居民人均生活用水量为,
故答案为:139,135;
(3)
根据题意得,
①2020年居民人均生活用水量在范围的省级行政区有3个,2019年居民人均生活用水量在范围的省级行政区有4个,
年居民人均生活用水量在范围的省级行政区的数量比2019年少,
推断①合理;
②由年和2020年居民人均生活用水量统计图得:
2019年居民人均生活用水量在范围的这个省级行政区2020年居民人均生活用水量在范围.
推断②合理;
故答案为:①②.
【点睛】本题主要考查了统计图的识别与应用,关键是正确识别统计图.
24.(1)60,21,30%;
(2)画图见解析
(3)该校每天课后进行体育锻炼的时间超过60分钟的学生共有330人.
【分析】(1)由A的人数除以所占百分比求出样本容量,进而求出a,b的值,即可解决问题;
(2)将频数分布直方图补充完整即可;
(3)由该校学生总人数乘以每天课后进行体育锻炼的时间超过60分钟的学生所占的百分比即可.
(1)
解:本次调查的样本容量是:12÷20%=60,
则a=60-12-18-6-3=21,b=18÷60×100%=30%,
故答案为:60,21,30%;
(2)
将频数分布直方图补充完整如下:
(3)
2200×(10%+5%)=330(人),
即该校每天课后进行体育锻炼的时间超过60分钟的学生共有330人.
【点睛】本题考查的是频数分布表与频数分布直方图,补全频数分布直方图,利用样本估计总体,掌握以上基础的统计知识是解本题的关键.
25.(1)见解析
(2)估计小钢同学所居住的小区110户家庭年收入不低于13万元
【分析】(1)先求出:年收入在的户数,然后补全统计图和统计表即可;
(2)用440乘以样本中年收入不低于13万元的户数占比即可.
【详解】(1)解:年收入在的户数为(户),
∴补全统计图(表)如下:
年收入分钟(万元) 划记 频数
丅 2
正一 6
正正正 18
正 9
3
丅 2
(2)解:户,
∴估计小钢同学所居住的小区110户家庭年收入不低于13万元.
【点睛】本题主要考查了频数分布表,频数分布直方图,用样本估计总体,正确读懂统计图是解题的关键.
