5.7+三角函数的应用课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共27张PPT)
文档属性
| 名称 | 5.7+三角函数的应用课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共27张PPT) | 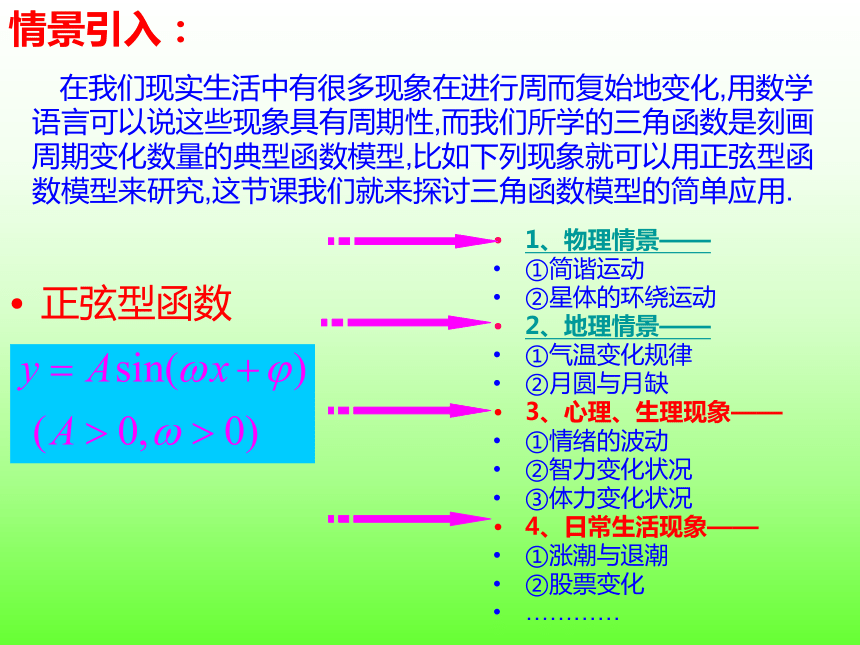 | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 15:54:17 | ||
图片预览






文档简介
(共27张PPT)
情景引入:
1、物理情景——
①简谐运动
②星体的环绕运动
2、地理情景——
①气温变化规律
②月圆与月缺
3、心理、生理现象——
①情绪的波动
②智力变化状况
③体力变化状况
4、日常生活现象——
①涨潮与退潮
②股票变化
…………
正弦型函数
在我们现实生活中有很多现象在进行周而复始地变化,用数学语言可以说这些现象具有周期性,而我们所学的三角函数是刻画周期变化数量的典型函数模型,比如下列现象就可以用正弦型函数模型来研究,这节课我们就来探讨三角函数模型的简单应用.
第一章 统计案例
5.7
三角函数的应用
高一数学必修第一册 第五章 三角函数
学习目标
了解y=Asin( x+ ) 的图象的物理意义,能指出简谐运动的振幅、周期、相位、初相。
2.会用三角函数解决简单的实际问题,体会可以利用三角函数构建刻画事物周期变化的数学模型;
3.能用三角函数模型解决一些具有周期变化规律的实际问题.
4.核心素养:直观想象、数学抽象、数学建模.
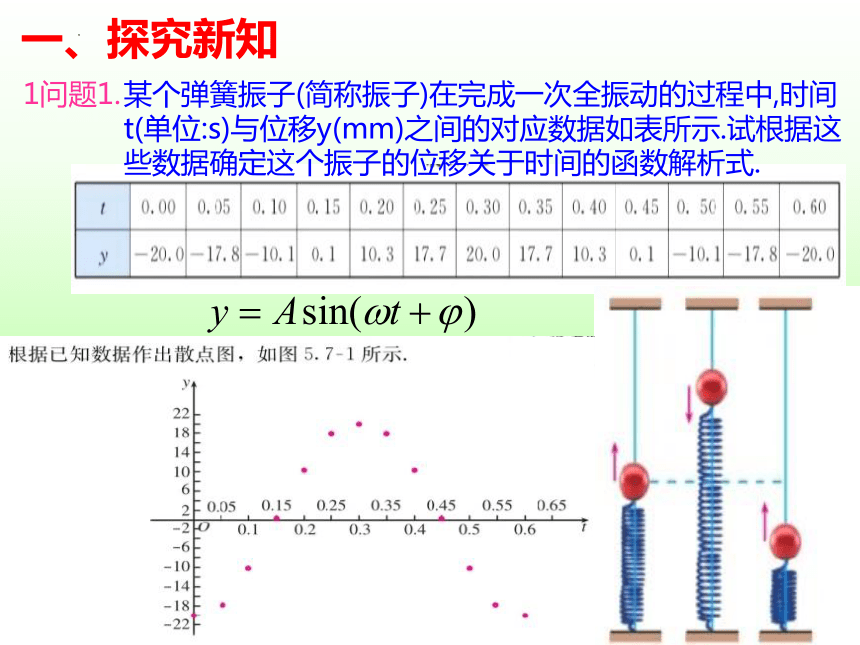
一、探究新知
某个弹簧振子(简称振子)在完成一次全振动的过程中,时间t(单位:s)与位移y(mm)之间的对应数据如表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
1问题1.
某个弹簧振子(简称振子)在完成一次全振动的过程中,时间t(单位:s)与位移y(mm)之间的对应数据如表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
问题1.
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动,等等. 这些都是物体在某一中心位置附近循环往复运动.在物理学中, 把物体受到力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.可以证明,在适当的直角坐标系下,简谐振动可以用函数
描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
A就是简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大距离;
这个简谐运动的周期是 ,它是简谐运动的物体往复运动一次所需
要的时间;
这个简谐运动的频率是由公式 ,它是简谐运动的物体往复
运动一次所需要的时间;
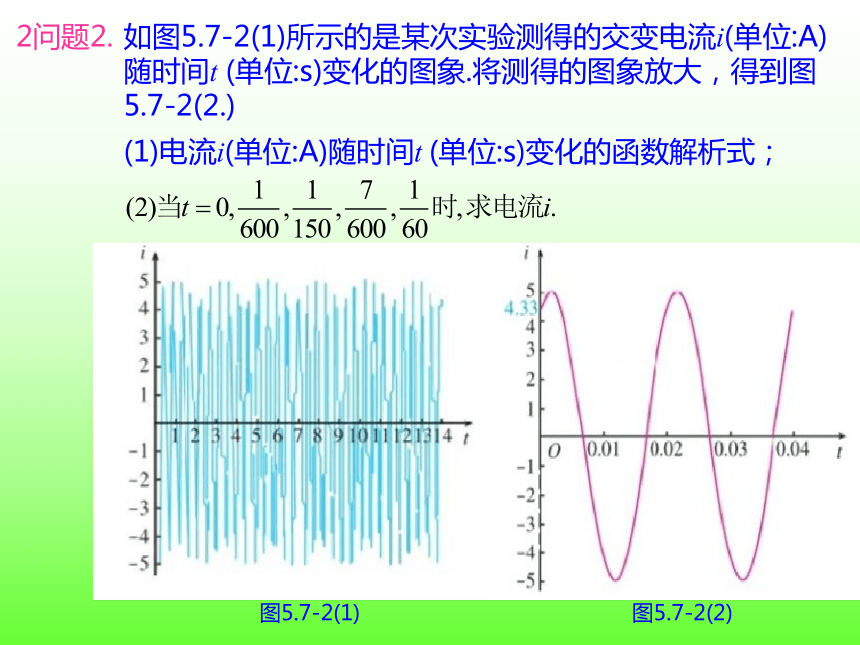
2问题2.
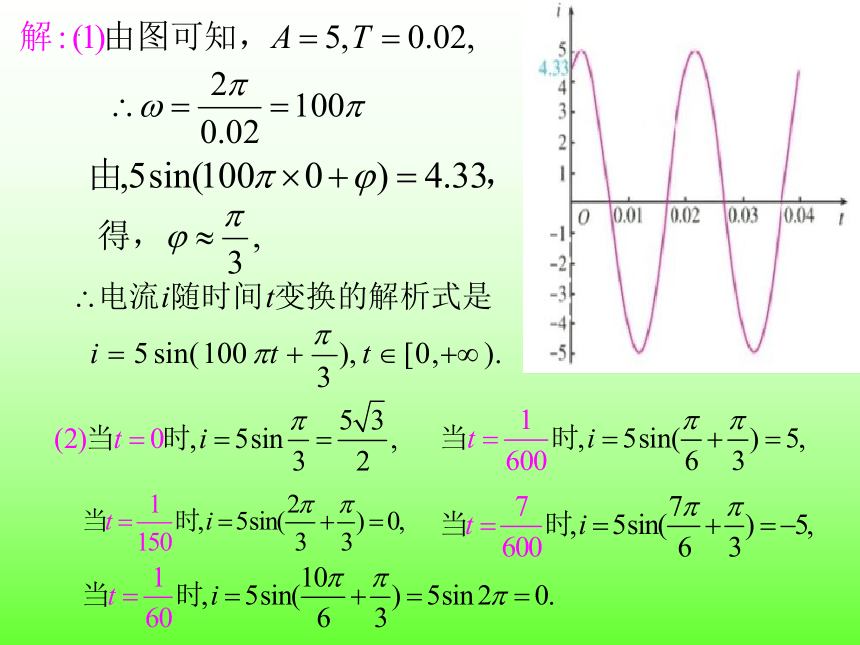
如图5.7-2(1)所示的是某次实验测得的交变电流i(单位:A)随时间t (单位:s)变化的图象.将测得的图象放大,得到图5.7-2(2.)
(1)电流i(单位:A)随时间t (单位:s)变化的函数解析式;
图5.7-2(1)
图5.7-2(2)
3.由图象求振幅A
3.由图象求振幅A
如图1.6-1,某地一天从6~14时的温度变化曲线近似 满足函数
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
二、巩固新知
1例1.
解:(1)由图可知,这段时间的最大温差是200C.
(2)从图中可以看出,从6~14时的图象是函数
的半个周期的图象,
综上,所求解析式为
一般取:| |≤π
2变式:函数 在一个周期内的图象
如图所示,此函数 的解析式为
y/cm
x/s
O
A
B
C
D
E
F
0.4
0.8
1.2
2
y
x
1
2
3
-1
三、课堂检测
解:由图可知
综上,所求解析式为
y
x
1
2
3
-1
1.本节课你学习了哪些基本知识?
2.本节课你学会了哪些思想方法?
函数思想
四、课堂小结
作业:(1)课本P249 习题5.7 2题
(2)做完资料对应习题
第一章 统计案例
5.7
三角函数的应用(2)
高一数学必修第一册 第五章 三角函数
学习目标
了解y=Asin( x+ ) 的图象的物理意义,能指出简谐运动的振幅、周期、相位、初相。
2.会用三角函数解决简单的实际问题,体会可以利用三角函数构建刻画事物周期变化的数学模型;
3.能用三角函数模型解决一些具有周期变化规律的实际问题.
4.核心素养:直观想象、数学抽象、数学建模.
海水受日月的引力作用,在一定的时候发生涨落的现象叫潮 . 一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是港口在某季节每天的时间与水深关系的表格:
选用函数y=Asin(ωt+φ)+b(A>0,ω>0)来模拟港口的水深与时间的关系.
(1)求港口的水深y与时间t之间的函数关系式.
(2)如果一条货船的吃水深度是5米,安全条例规定至少有6.5米 的安全间隙(船底与洋底的距离),则该船一天之内在港口内呆的时间总和为多少小时?
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深 10.0 13.0 9.9 7.0 10.0 13.0 9.9 7.0 10.0
1例1.
一、函数模型的应用
时刻 0:00 3:06 6:12 9:18 12:24 15:30 18:36 21:42 24:00
水深(米) 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 4.0
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似数值(精确到0.001).
海水受日月的引力,在一定的时候发生涨落的现象叫潮. 一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋. 下面是某港口某天的时刻与水深关的预报.
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5m的安全间隙(船底与洋底的距离),该船何时能进入港口 在港口能呆多久
2例2.
O
x
y
3
6
9
12
15
18
21
24
2
4
6
时刻 0:00 3:06 6:12 9:18 12:24 15:30 18:36 21:42 24:00
水深(米) 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 4.0
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似数值(精确到0.001).
海水受日月的引力,在一定的时候发生涨落的现象叫潮. 一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋. 下面是某港口某天的时刻与水深关的预报.
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5m的安全间隙(船底与洋底的距离),该船何时能进入港口 在港口能呆多久
2例2.
时刻 0:00 3:06 6:12 9:18 12:24 15:30 18:36 21:42 24:00
水深(米) 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 4.0
海水受日月的引力,在一定的时候发生涨落的现象叫潮. 一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋. 下面是某港口某天的时刻与水深关的预报.
2例2.
t 0 3 6 9 12 15 18 21 24
y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
课堂检测
1.本节课你学习了哪些基本知识?
2.本节课你学会了哪些思想方法?
函数思想
五、课堂小结
作业:(1)课本P255 习题5.7 23 、 25题
(2)做完资料对应习题
情景引入:
1、物理情景——
①简谐运动
②星体的环绕运动
2、地理情景——
①气温变化规律
②月圆与月缺
3、心理、生理现象——
①情绪的波动
②智力变化状况
③体力变化状况
4、日常生活现象——
①涨潮与退潮
②股票变化
…………
正弦型函数
在我们现实生活中有很多现象在进行周而复始地变化,用数学语言可以说这些现象具有周期性,而我们所学的三角函数是刻画周期变化数量的典型函数模型,比如下列现象就可以用正弦型函数模型来研究,这节课我们就来探讨三角函数模型的简单应用.
第一章 统计案例
5.7
三角函数的应用
高一数学必修第一册 第五章 三角函数
学习目标
了解y=Asin( x+ ) 的图象的物理意义,能指出简谐运动的振幅、周期、相位、初相。
2.会用三角函数解决简单的实际问题,体会可以利用三角函数构建刻画事物周期变化的数学模型;
3.能用三角函数模型解决一些具有周期变化规律的实际问题.
4.核心素养:直观想象、数学抽象、数学建模.
一、探究新知
某个弹簧振子(简称振子)在完成一次全振动的过程中,时间t(单位:s)与位移y(mm)之间的对应数据如表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
1问题1.
某个弹簧振子(简称振子)在完成一次全振动的过程中,时间t(单位:s)与位移y(mm)之间的对应数据如表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
问题1.
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动,等等. 这些都是物体在某一中心位置附近循环往复运动.在物理学中, 把物体受到力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.可以证明,在适当的直角坐标系下,简谐振动可以用函数
描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
A就是简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大距离;
这个简谐运动的周期是 ,它是简谐运动的物体往复运动一次所需
要的时间;
这个简谐运动的频率是由公式 ,它是简谐运动的物体往复
运动一次所需要的时间;
2问题2.
如图5.7-2(1)所示的是某次实验测得的交变电流i(单位:A)随时间t (单位:s)变化的图象.将测得的图象放大,得到图5.7-2(2.)
(1)电流i(单位:A)随时间t (单位:s)变化的函数解析式;
图5.7-2(1)
图5.7-2(2)
3.由图象求振幅A
3.由图象求振幅A
如图1.6-1,某地一天从6~14时的温度变化曲线近似 满足函数
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
二、巩固新知
1例1.
解:(1)由图可知,这段时间的最大温差是200C.
(2)从图中可以看出,从6~14时的图象是函数
的半个周期的图象,
综上,所求解析式为
一般取:| |≤π
2变式:函数 在一个周期内的图象
如图所示,此函数 的解析式为
y/cm
x/s
O
A
B
C
D
E
F
0.4
0.8
1.2
2
y
x
1
2
3
-1
三、课堂检测
解:由图可知
综上,所求解析式为
y
x
1
2
3
-1
1.本节课你学习了哪些基本知识?
2.本节课你学会了哪些思想方法?
函数思想
四、课堂小结
作业:(1)课本P249 习题5.7 2题
(2)做完资料对应习题
第一章 统计案例
5.7
三角函数的应用(2)
高一数学必修第一册 第五章 三角函数
学习目标
了解y=Asin( x+ ) 的图象的物理意义,能指出简谐运动的振幅、周期、相位、初相。
2.会用三角函数解决简单的实际问题,体会可以利用三角函数构建刻画事物周期变化的数学模型;
3.能用三角函数模型解决一些具有周期变化规律的实际问题.
4.核心素养:直观想象、数学抽象、数学建模.
海水受日月的引力作用,在一定的时候发生涨落的现象叫潮 . 一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是港口在某季节每天的时间与水深关系的表格:
选用函数y=Asin(ωt+φ)+b(A>0,ω>0)来模拟港口的水深与时间的关系.
(1)求港口的水深y与时间t之间的函数关系式.
(2)如果一条货船的吃水深度是5米,安全条例规定至少有6.5米 的安全间隙(船底与洋底的距离),则该船一天之内在港口内呆的时间总和为多少小时?
时刻 0:00 3:00 6:00 9:00 12:00 15:00 18:00 21:00 24:00
水深 10.0 13.0 9.9 7.0 10.0 13.0 9.9 7.0 10.0
1例1.
一、函数模型的应用
时刻 0:00 3:06 6:12 9:18 12:24 15:30 18:36 21:42 24:00
水深(米) 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 4.0
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似数值(精确到0.001).
海水受日月的引力,在一定的时候发生涨落的现象叫潮. 一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋. 下面是某港口某天的时刻与水深关的预报.
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5m的安全间隙(船底与洋底的距离),该船何时能进入港口 在港口能呆多久
2例2.
O
x
y
3
6
9
12
15
18
21
24
2
4
6
时刻 0:00 3:06 6:12 9:18 12:24 15:30 18:36 21:42 24:00
水深(米) 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 4.0
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似数值(精确到0.001).
海水受日月的引力,在一定的时候发生涨落的现象叫潮. 一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋. 下面是某港口某天的时刻与水深关的预报.
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5m的安全间隙(船底与洋底的距离),该船何时能进入港口 在港口能呆多久
2例2.
时刻 0:00 3:06 6:12 9:18 12:24 15:30 18:36 21:42 24:00
水深(米) 5.0 7.5 5.0 2.5 5.0 7.5 5.0 2.5 4.0
海水受日月的引力,在一定的时候发生涨落的现象叫潮. 一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后,在落潮时返回海洋. 下面是某港口某天的时刻与水深关的预报.
2例2.
t 0 3 6 9 12 15 18 21 24
y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
课堂检测
1.本节课你学习了哪些基本知识?
2.本节课你学会了哪些思想方法?
函数思想
五、课堂小结
作业:(1)课本P255 习题5.7 23 、 25题
(2)做完资料对应习题
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
