中考复习-二次函数的图像与性质

课件40张PPT。二次函数的图象与性质(复习一) 考 点 聚 焦归 类 探 究┃二次函数的图象与性质(一)考 点 聚 焦考点1 二次函数的概念 定义：一般地，如果______________(a，b，c是常数，a≠0)，那么y叫做x的二次函数．y＝ax2＋bx＋c┃二次函数的图象与性质(一)探究一 二次函数的定义 命题角度：
1．二次函数的概念；
2．二次函数的形式．A考点聚焦归类探究归 类 探 究┃二次函数的图象与性质(一)考点聚焦归类探究
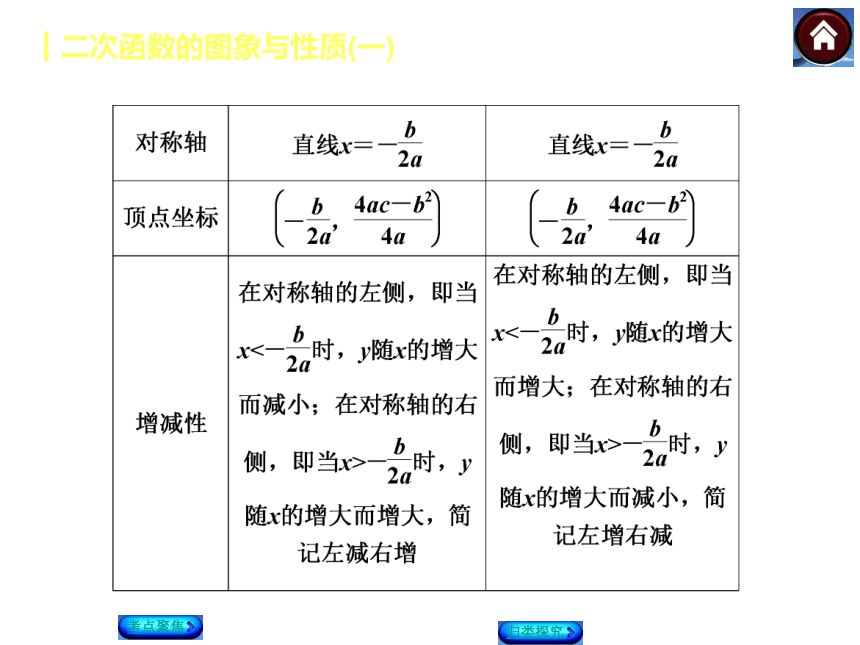
利用二次函数的定义判定，二次函数中自变量的最高次数是2，且二次项的系数不为0.┃二次函数的图象与性质(一)考点聚焦归类探究考点2 二次函数的图象及画法y＝a(x－h)2＋k ┃二次函数的图象与性质(一)考点聚焦归类探究考点3 二次函数的性质 ┃二次函数的图象与性质(一)考点聚焦归类探究┃二次函数的图象与性质(一)考点聚焦归类探究┃二次函数的图象与性质(一)探究二 二次函数的图象与性质 命题角度：
1. 二次函数的图象及画法；
2. 二次函数的性质．考点聚焦归类探究　 例2 [2012·烟台] 已知二次函数y＝2(x－3)2＋1.下列说法：①其图象的开口向下；②其图象的对称轴为直线x＝－3；③其图象的顶点坐标为(3，－1)；④当x＜3时，y随x的增大而减小． ⑤ 若点（ ，b ）与点（ , d ）在此函数图像上时，b > d , 则其中说法正确的有(　　)
A． 1个 B．2个
C ． 3个 D．4个A ┃二次函数的图象与性质(一)考点聚焦归类探究考点4 用待定系数法求二次函数的解析式 ┃二次函数的图象与性质(一)考点聚焦归类探究┃二次函数的图象与性质(一)探究三 二次函数的解析式的求法 命题角度：
1. 一般式，顶点式，交点式；
2. 用待定系数法求二次函数的解析式．考点聚焦归类探究?第14课时┃归类探究解 析　　根据题目要求，本题可选用多种方法求关系式． 解考点聚焦归类探究第14课时┃归类探究 解第14课时┃归类探究解 析考点聚焦归类探究第14课时┃归类探究解 析考点聚焦归类探究第14讲┃二次函数的图象与性质(一)考点聚焦归类探究 (1)当已知抛物线上三点求二次函数的解析式时，一般采用一般式y＝ax2＋bx＋c(a≠0)；(2)当已知抛物线顶点坐标(或对称轴及最大或最小值)求解析式时，一般采用顶点式y＝a(x－h)2＋k；(3)当已知抛物线与x轴的交点坐标求二次函数的解析式时，一般采用交点式y＝a(x－x1)(x－x2)．考点5 二次函数与一元二次方程、不等式的关系┃ 例4 若关于x的二次函数y＝kx2 +2x-1
与x轴有公共点，则实数k的值为多少？
变式：（2013黄石）若关于x的函数y＝kx2 +2x-1
与x轴仅有一个公共点，则实数k的值为多少？
┃二次函数的图象与性质(二)考点聚焦归类探究考点6 二次函数y＝ax2＋bx＋c(a≠0)的图象特征与a、b、c的符号之间的关系┃二次函数的图象与性质(二)考点聚焦归类探究┃二次函数的图象与性质(二)探究 二次函数的图象特征与a，b，c之间的关系 命题角度：
1. 二次函数的图象的开口方向，对称轴，顶点坐标，与坐标轴的交点情况与a，b，c的关系；
2. 图象上的特殊点与a，b，c的关系．考点聚焦归类探究┃二次函数的图象与性质(二)C考点聚焦归类探究图15－4┃二次函数的图象与性质(二)解　析　考点聚焦归类探究┃二次函数的图象与性质(二)考点聚焦归类探究┃二次函数的图象与性质(二)考点聚焦归类探究考点7 二次函数图象的平移 将抛物线y＝ax2＋bx＋c(a≠0)用配方法化成y＝a(x－h)2＋k(a≠0)的形式，而任意抛物线y＝a(x－h)2＋k均可由抛物线y＝ax2平移得到，具体平移方法如图15－1：图15－1 ┃二次函数的图象与性质(二)探究 二次函数的图象的平移 命题角度：
1. 二次函数的图象的平移规律；
2. 利用平移求二次函数的图象的解析式．考点聚焦归类探究　 例7 [2013·雅安] 将抛物线y= x2－ 2x+4向左平移1个位，再向下平移3个单位后所得抛物线的解析式为(　　)
A．y＝(x－2)2
B．y＝(x－2)2＋6
C．y＝x2＋6
D．y＝x2D ┃二次函数的图象与性质(二)考点聚焦归类探究 二次函数的平移，先把y＝ax2＋bx＋c化为y＝a(x－h)2＋k，由x－h＝0得x＝h，当h>0向右移，h<0向左移，k>0向上移，k<0向下移．即左加右减，上加下减。 ┃二次函数的图象与性质(二)解　析　将抛物线化为顶点式：y＝(x－1)2＋3向左平移1个单位所得直线解析式为y＝(x－1＋1)2＋3，即y＝x2＋3；
再向下平移3个单位为y＝x2＋3－3，即y＝x2.
故选D.考点聚焦归类探究┃二次函数的图象与性质(二)考点聚焦归类探究　 图15－2B ┃二次函数的图象与性质(二)解　析　考点聚焦归类探究┃二次函数的图象与性质(二)考点聚焦归类探究 二次函数的图象特征主要从开口方向、与x轴有无交点，与y轴的交点及对称轴的位置，确定a，b，c及b2－4ac的符号，有时也可把x的值代入，根据图象确定y的符号．┃二次函数的图象与性质(二)命题角度：
二次函数的图象与性质的综合运用．考点聚焦归类探究探究七　二次函数的图象与性质的综合运用 例10 [2013·内江] 已知二次函数y＝ax2＋bx＋c(a>0)的图象与x轴交于A(x1，0)，B(x2，0)(x1(1)若抛物线的顶点为D，求S△ABC∶S△ACD的值；
(2)若∠ADC＝90°，求二次函数的解析式．图15－5 ┃二次函数的图象与性质(二)考点聚焦归类探究 解　　┃二次函数的图象与性质(二)考点聚焦归类探究谢谢！